LeetCode862 和至少为k的最短子数组
题目:

解析:
1、先构造前缀和数组
2、单调队列存放滑动窗口,目的求Sj-Si >=k的情况下,窗口最小。
代码:
class Solution {public int shortestSubarray(int[] nums, int k) {int n = nums.length;long[] sums = new long[n + 1]; // 注意这里加和后,容易超过int,加和用long数组for (int i = 1; i <= n; i++) {sums[i] = sums[i - 1] + nums[i - 1];}Deque<Integer> deque = new LinkedList<>();deque.add(0);int res = Integer.MAX_VALUE;for (int i = 1; i <= n; i++) {while (!deque.isEmpty() && sums[i] - sums[deque.peek()] >= k) { // 注意边界,求最小这里应该 >=res = Math.min(res, i - deque.poll());}//将所有大于等于s[i]的数删掉 问题:这里不删能怎么样,上面求最小值会守影响么?while (!deque.isEmpty() && sums[deque.peekLast()] >= sums[i]) { // 注意边界,求最小这里应该 >=deque.pollLast();}deque.add(i);}if (res == Integer.MAX_VALUE) {return -1;}return res;}
}
相关文章:

LeetCode862 和至少为k的最短子数组
题目: 解析: 1、先构造前缀和数组 2、单调队列存放滑动窗口,目的求Sj-Si >k的情况下,窗口最小。 代码: class Solution {public int shortestSubarray(int[] nums, int k) {int n nums.length;long[] sums new …...

网卡bonding模式 - bond模式配置介绍
网卡bonding简介 网卡绑定就是把多张物理网卡通过软件虚拟成一个虚拟的网卡,配置完毕后,所有的物理网卡的ip和mac将会变成相同的。多网卡同时工作可以提高网络速度,还可以实现网卡的负载均衡、冗余。 bonding模式 1 round-robin(mode0) 轮转…...

做了个 chrome 插件实现 B 站视频截图功能,直接从当前视频帧无损复制
起因是看 B 站视频想截个图很麻烦,右下角暂停按钮无法去除,于是写了一行代码把暂停按钮隐藏。 后经提醒,发现可以通过 canvas 获取视频帧来截取图片,于是写了如下代码完美获取视频帧。 var v document.querySelector(".bpx…...

Docker linux 安装
sudo yum update sudo yum clean all sudo yum makecache#安装依赖 sudo yum install -y yum-utils device-mapper-persistent-data lvm2 #添加官方存储库 sudo yum-config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo#安装-跳过一些异常依赖…...
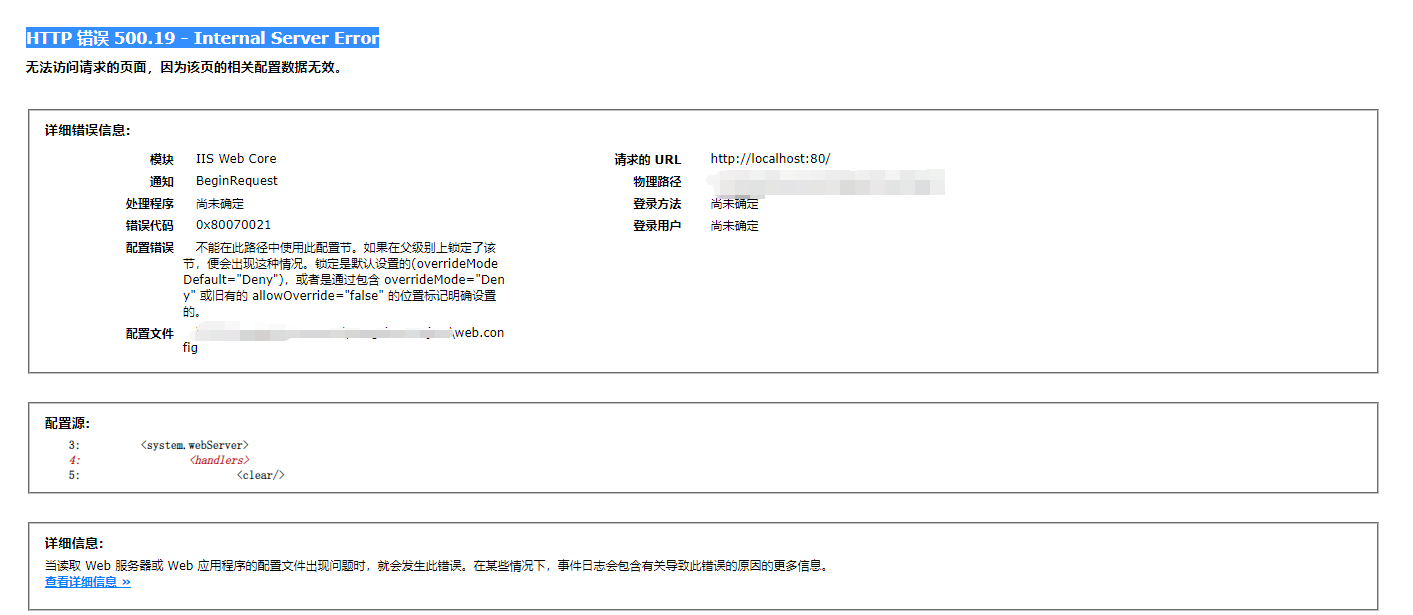
windows部署django服务器
windows部署django服务器 1、安装IIS1.1 控制面板-----程序----程序和功能----启用或关闭windows功能1.2安装IIS服务器,完成后,重新进入,把CGI安装进系统 2、安装python与虚拟环境2.1 安装python2.2 安装virtualenv虚拟环境2.3 创建一个虚拟环…...

ChatGPT prompt汇总-个人使用-持续更新....
用途 学术写作更新记录 学术写作 中译英(GPT-4) I am a researcher studying deep learning and now trying to revise my manuscript which will be submitted to the Journal of Nature . I want you to act as a scientific English-Chinese translator, I will provide yo…...
Vue实现简单的接口封装
1. 在src中创建一个api文件夹 2. 按功能、模块等新建对应的js文件 3. 在内部写对应的封装接口,并导出 import axios from "axios";/*** 接口名称:* 接收参数:* 返回参数:* */export const miens ()>{return new P…...

软件测试工具有什么作用?有哪些好用的测试工具推荐?
软件测试工具是现代软件测试中不可或缺的重要组成部分,指的是一系列在软件开发过程中使用的工具,用于帮助测试人员进行测试活动,提高测试效率,减少测试成本。选择并使用合适的软件测试工具,可提高软件质量和效率。 一…...
写爬虫?前端er何必用python
前言 说起网络爬虫,很多人第一时间想到python,但爬虫并非只能用python实现,虽然网上大部分爬虫文章都在说python爬虫,但对于前端程序员来说,我觉得js才是最屌的(对于简单爬取任务来说,复杂的我暂时没碰到~),下面说说我的经验(是的,仅限本人经验),希望能给各位前…...

交通物流模型 | 基于交通图卷积长短时记忆网络的网络级交通流预测
交通物流模型 | 基于交通图卷积长短时记忆网络的网络级交通流预测 由于道路网络时变的交通模式和复杂的空间依赖性,交通流预测是一个具有挑战性的时空预测问题。为了克服该挑战,作者将交通网络看为一张图,并提出一个新的深度学习预测模型,交通图卷积长短时记忆网络(TGC-L…...

web 基础和http 协议
一、域名 域名的概念 IP地址不易记忆,域名方便记住,以便于用户进行搜索访问 早期使用Hosts文件解析域名地址 缺点: ① 主机名称重复 ② 主机维护困难 DNS(Domain Name System)域名系统 ① 分布式 将一个大的数…...

Java常量与变量
Java常量与变量 在程序执行过程中,其值不能被改变的量称为常量,其值能被改变的量称为变量。 Java关键字 Java关键字 int public (公有的,可跨包) new finally throw (抛出一个异常对象) continuefloatlongshort extends (继承,用于类继承类) returnbrea…...
神经网络中卷积和池化的区别
1、什么叫卷积? 卷积层是用一个固定大小的矩形区去席卷原始数据,将原始数据分成一个个和卷积核大小相同的小块,然后将这些小块和卷积核相乘输出一个卷积值(注意这里是一个单独的值,不再是矩阵了)。 卷积的…...

RK3568平台开发系列讲解(驱动篇)RK3568 PWM详解
🚀返回专栏总目录 文章目录 一、什么是PWM二、RK3568 PWM2.1、PWM 通道与引脚2.2、PWM 简介2.3、PWM 设备节点沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 PWM 是很常用到功能,我们可以通过 PWM 来控制电机速度,也可以使用 PWM 来控制 LCD 的背光亮度。 一、什…...

禾匠商城系统 企业转账到零钱 修改成 商家转账到零钱
注意php 7以上的json_encode 溢出 修改的路径: vendor/luweiss/wechat/src/Wechat/WechatPay.php <?phpnamespace luweiss\Wechat;class WechatPay extends WechatBase {const SIGN_TYPE_MD5 MD5;const TRADE_TYPE_JSAPI JSAPI;const TRADE_TYPE_NATIVE NA…...

点云从入门到精通技术详解100篇-基于激光点云的道路目标检测
目录 前言 国内外研究现状 点云目标检测算法的研究现状 激光雷达相关技术 2.1 引言...
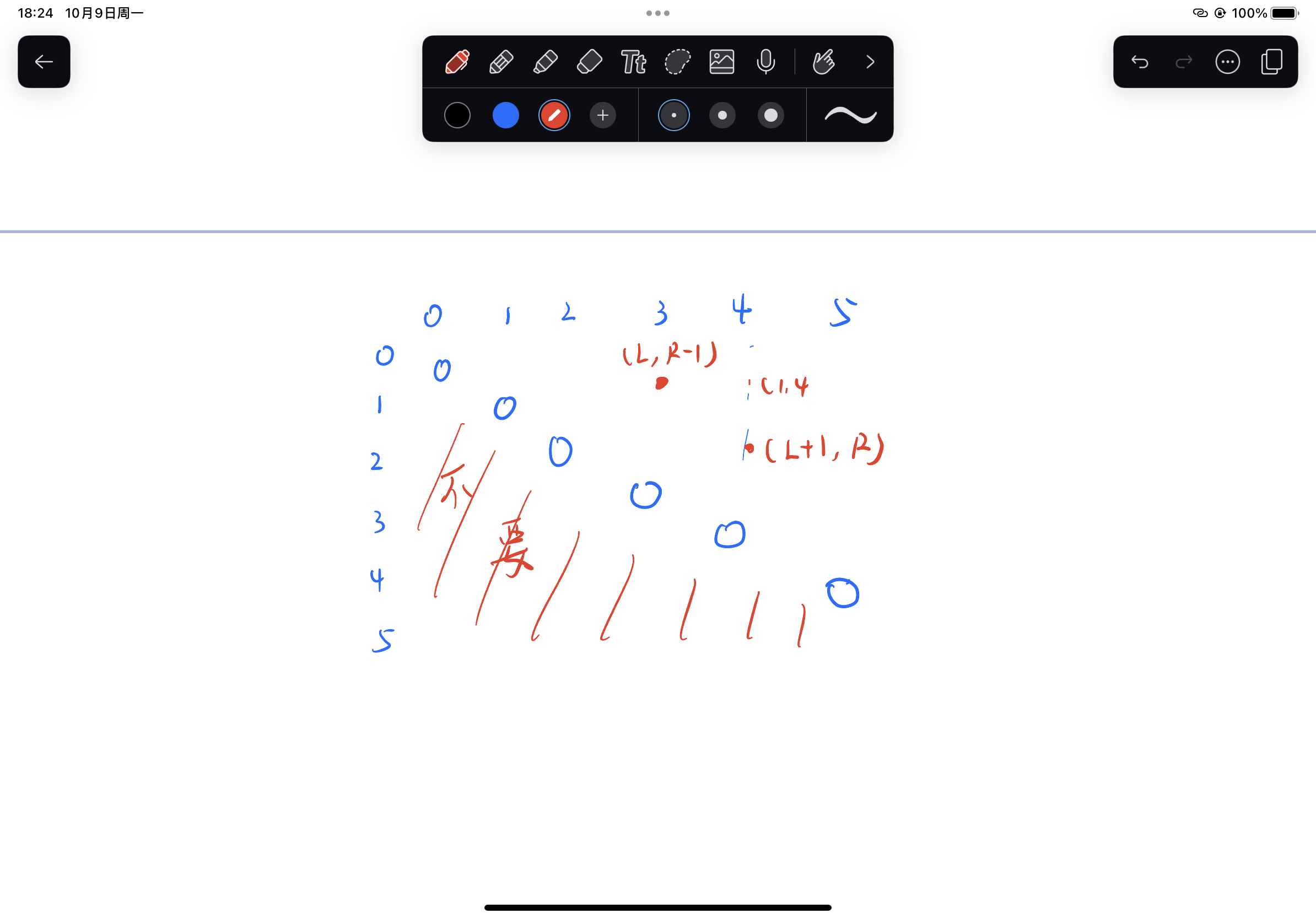
【Hello Algorithm】暴力递归到动态规划(一)
暴力递归到动态规划(一) 斐波那契数列的动态规划机器人走路初级递归初级动态规划动态规划 先后选牌问题初级递归初级动态规划动态规划 我们可以一句话总结下动态规划 动态规划本质是一种以空间换时间的行为 如果你发现有重复调用的过程 在经过一次之后把…...
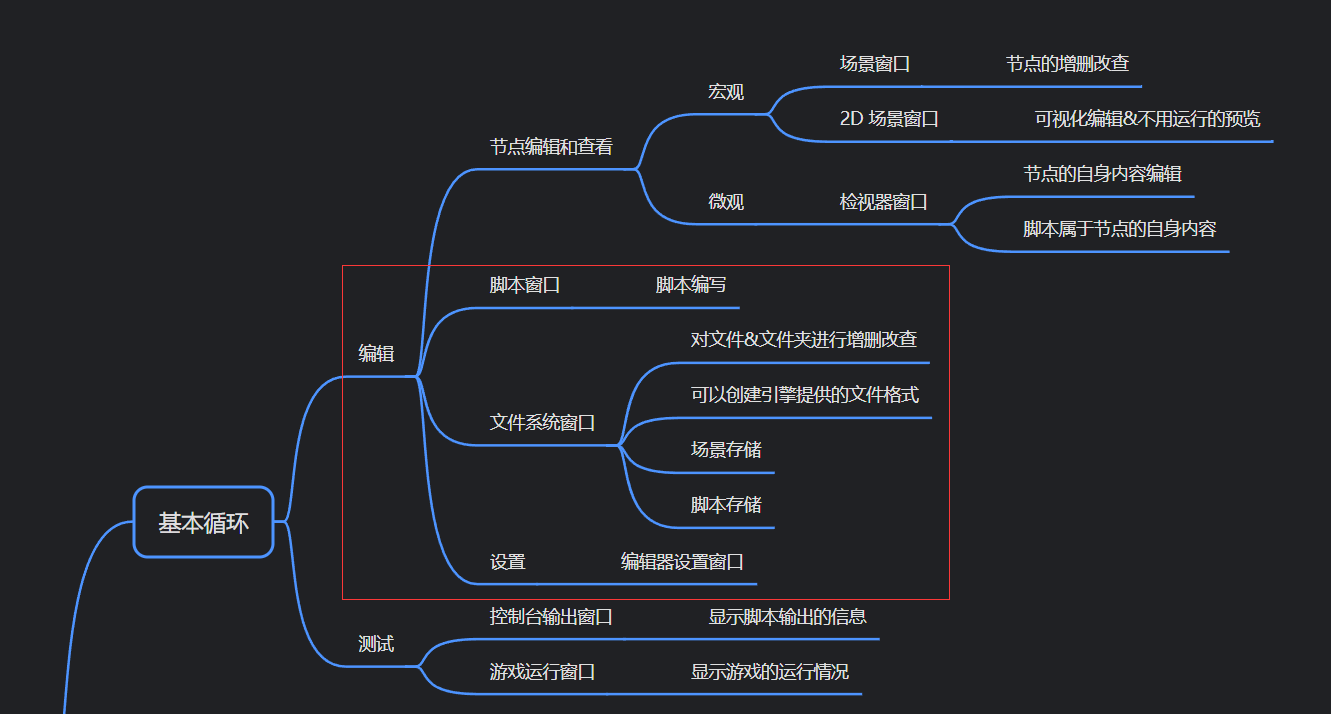
凉鞋的 Godot 笔记 107. 脚本窗口文件系统窗口
107. 脚本窗口&文件系统窗口 在上一篇,我们完成了第二轮循环,同时也接触了一些新内容,如下所示: 频率使用比较高的窗口,还剩下最后两个了,一个是脚本窗口: 另一个是文件系统窗口: 脚本窗口 和 文件系统…...

数据源作用以及spring配置数据源
数据源 数据源,简单理解为数据源头,提供了应用程序所需要数据的位置。数据源保证了应用程序与目标数据之间交互的规范和协议,它可以是数据库,文件系统等等。其中数据源定义了位置信息,用户验证信息和交互时所需的一些…...

Javaweb中的servlet中的消息体是什么?
2023年10月9日,周一晚上 目录 什么是消息体 什么是HTTP响应 HTTP响应由谁产生,发给谁 响应头具体有什么内容 Content-Type的值怎么写 HTTP响应例子 什么是消息体 消息体(message body)指HTTP响应中的实体主体内容。 什么是HTTP响应 在HTTP响应中…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
