【Hello Algorithm】暴力递归到动态规划(一)
暴力递归到动态规划(一)
- 斐波那契数列的动态规划
- 机器人走路
- 初级递归
- 初级动态规划
- 动态规划
- 先后选牌问题
- 初级递归
- 初级动态规划
- 动态规划
我们可以一句话总结下动态规划
动态规划本质是一种以空间换时间的行为 如果你发现有重复调用的过程 在经过一次之后把结果记下来 下次调用的时候直接用 这就是动态规划
斐波那契数列的动态规划
一般来说我们可以使用递归来解决斐波那契数列问题 代码如下
int fib(int n)
{ if (n <= 0) { cerr << "error" << endl; } if (n <= 2) { return 1; } return fib(n-1) + fib(n-2);
}
当然 这种方式会产生大量的重复计算 所以说我们可以保存上个和上上个的计算值来进行动态规划
int dpfib(int n)
{ if (n <= 2) { return 1; } int i = 1; int j = 1; int k = 0; while (n-2) { k = i + j; i = j; j = k; n--; } return k;
}
这样子写代码就能避免大量的重复计算了
机器人走路
初级递归
假设现在有1~N个位置
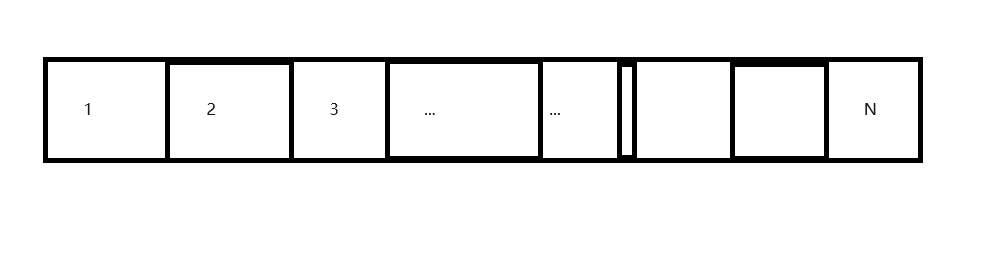
有一个小机器人 现在在START位置
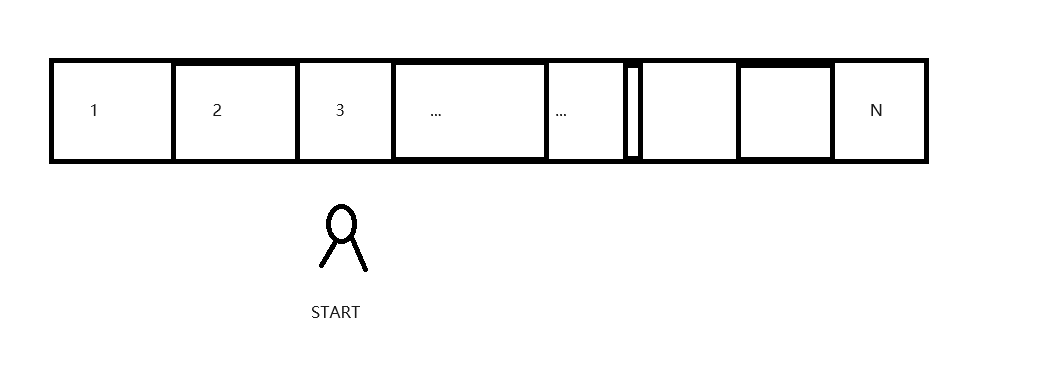
它现在要去aim位置 (aim为1~N上的随机一点) 能走K步 (K >= 0)
每次只能走一步 不能越界 不能停止 现在请问有多少种方式能走走到
现在假设 S = 2 N = 5 AIM = 4 K = 6
我们一开始写出的递归方程如下
int process1(int cur , int rest , int aim , int k)
参数含义如下
- cur 当前位置
- rest 剩余步数
- aim 目标地点
- k 能走的步数
base case为
- 如果剩余步数为0 则判断cur是否为aim地点
否则我们执行递归继续往下走
int process1(int cur , int rest , int aim , int n)
{ if (rest == 0){return cur == aim ? 1 : 0;}if (cur == 1){return process1(2 , rest -1 , aim , n);}if (cur == n){return process1(n-1 , rest-1 , aim , n);} return process1(cur-1 , rest-1 , aim , n)+ process1(cur+1 , rest-1 , aim , n);
}
初级动态规划
现在我们要进行进一步的动态规划
我们想想看在递归函数中有真正决定的是哪两个参数
我们每次传递参数的时候 aim 和 n 是不变的
其实每次变化的就是 cur 和 rest
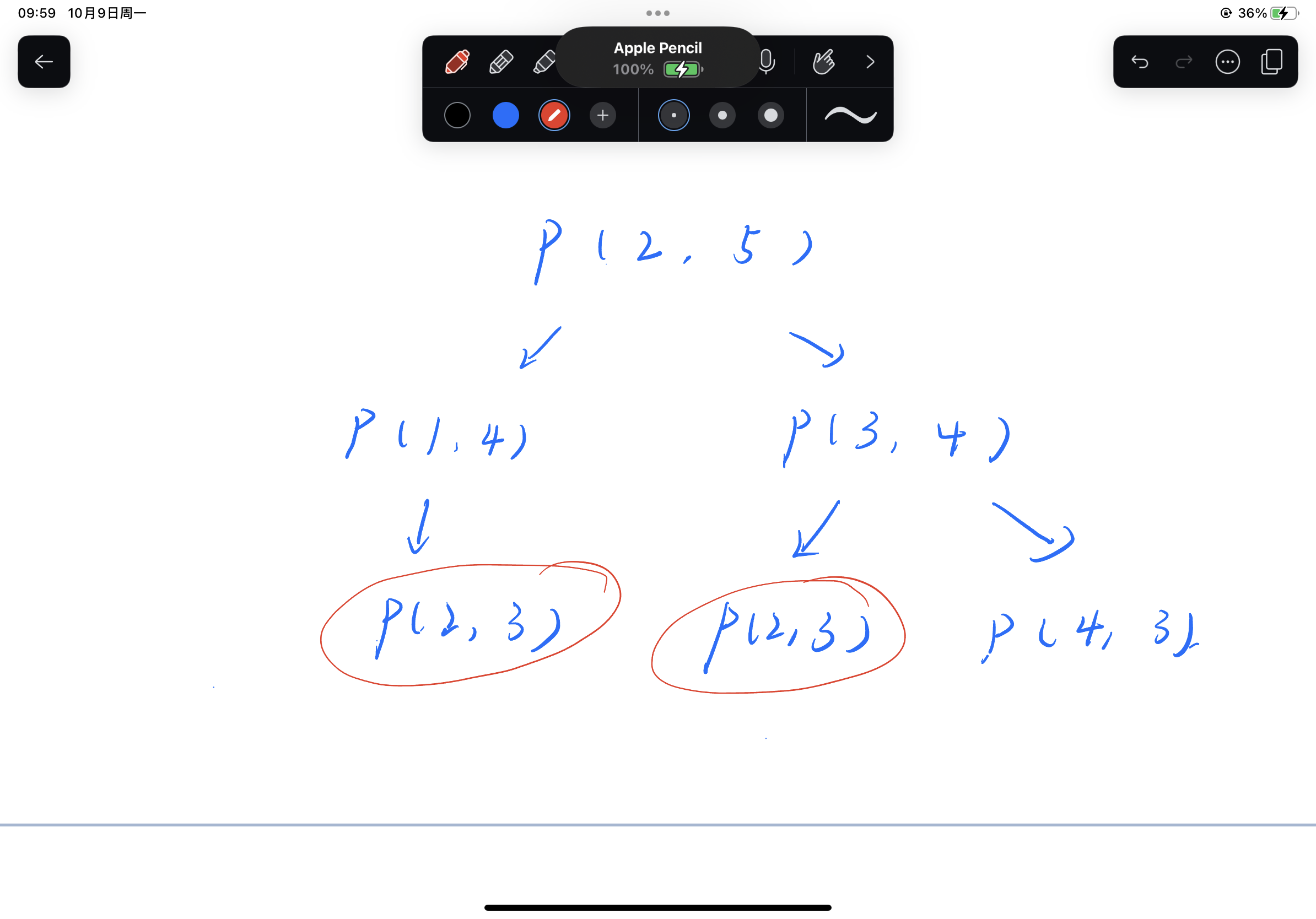
我们可以将该函数往下推演 我们会发现会出现两个相同的结果
如果继续往下展开的话则肯定会有重复的部分 所以说我们最好能将这些函数的结果记录下来 避免重复计算
我们选择使用一个二维数组存储每个函数的计算结果
vector<vector<int>> dp(n + 1 , vector<int>(rest + 1)); for (int i = 0 ; i < n + 1 ; i++ ) { for (int j = 0; j < rest + 1 ; j++) { dp[i][j] = -1; } }
这个二维数组 i j 分别标识当前位置和剩余步数
该数组的值表示在当前位置下走剩余步数能走到目的地有多少种解法
我们首先全部初始化为-1
int _process2(int cur , int rest , int aim , int n , vector<vector<int>>& dp)
{if (dp[cur][rest] != -1){return dp[cur][rest];}int ans = 0;if (rest == 0){ans = cur == aim ? 1 : 0;}else if (cur == 1){ans = _process2(2 , rest-1 , aim , n , dp);}else if (cur == n){ans = _process2(n-1 , rest-1 , aim , n , dp);} else {ans = _process2(cur -1 , rest -1 , aim , n , dp ) + _process2(cur +1 , rest -1 , aim , n , dp); } dp[cur][rest] = ans;return ans;}
之后在我们的函数中 如果数组中有结果 我们就直接返回 如果没有结果我们就将结果记录在数组中后返回 也能得到一样的结果
动态规划
我们以cur为横坐标 rest为纵坐标画一个图 并且将cur为0的时候值填入图中
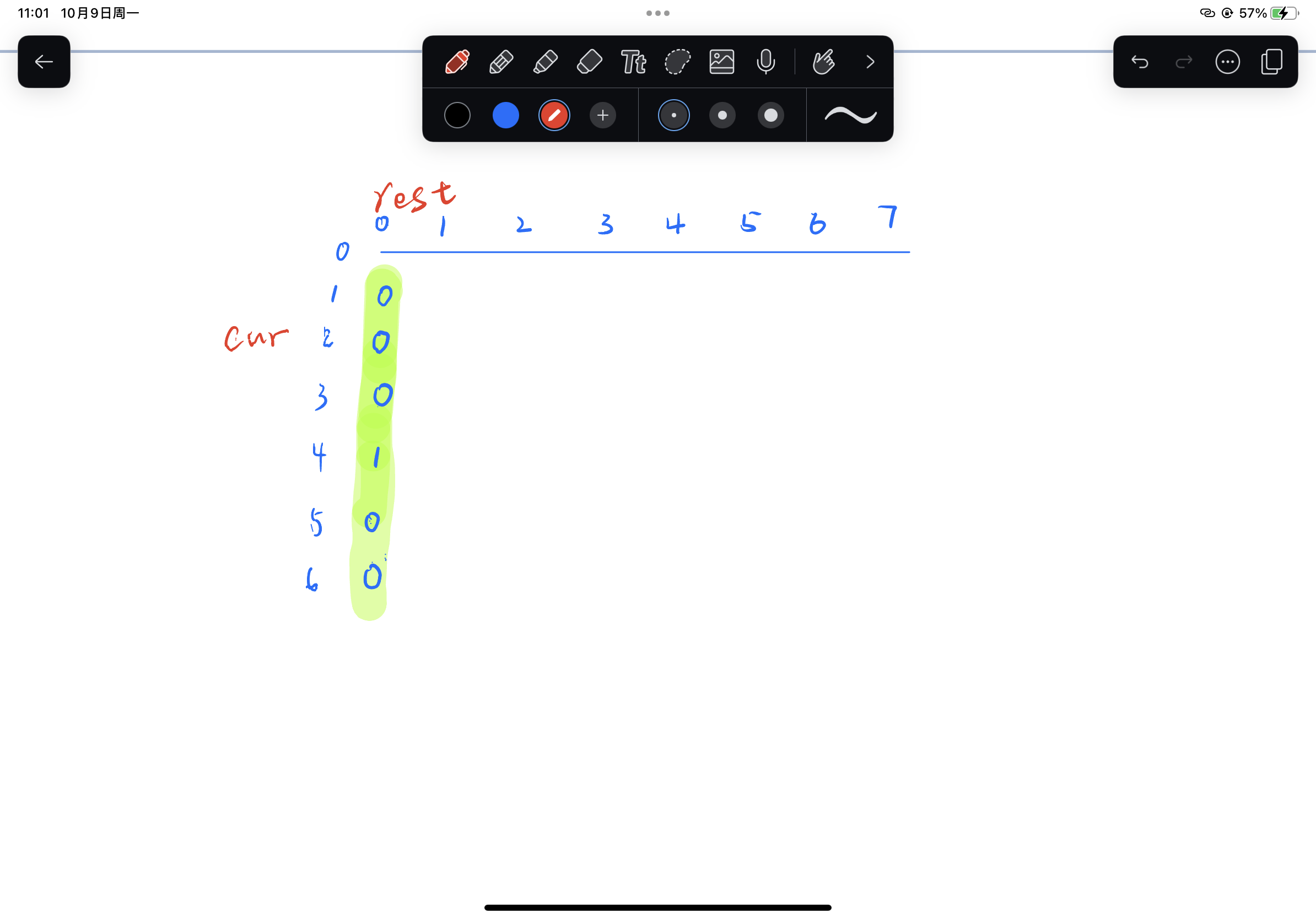
当cur为1的时候 我们回顾下我们的代码 我们会发现 此时该格上的数字只依赖于 dp[2][rest-1]
当cur为n的时候 我们回顾下之前的带啊吗 我们会发现 此时该格上的数字只依赖于 dp[n-1][rest-1]
当cur介于两者之间的时候 此时该格上的数字依赖于两种路径
dp[cur-1][rest-1] + dp[cur+1][rest-1]
如下图
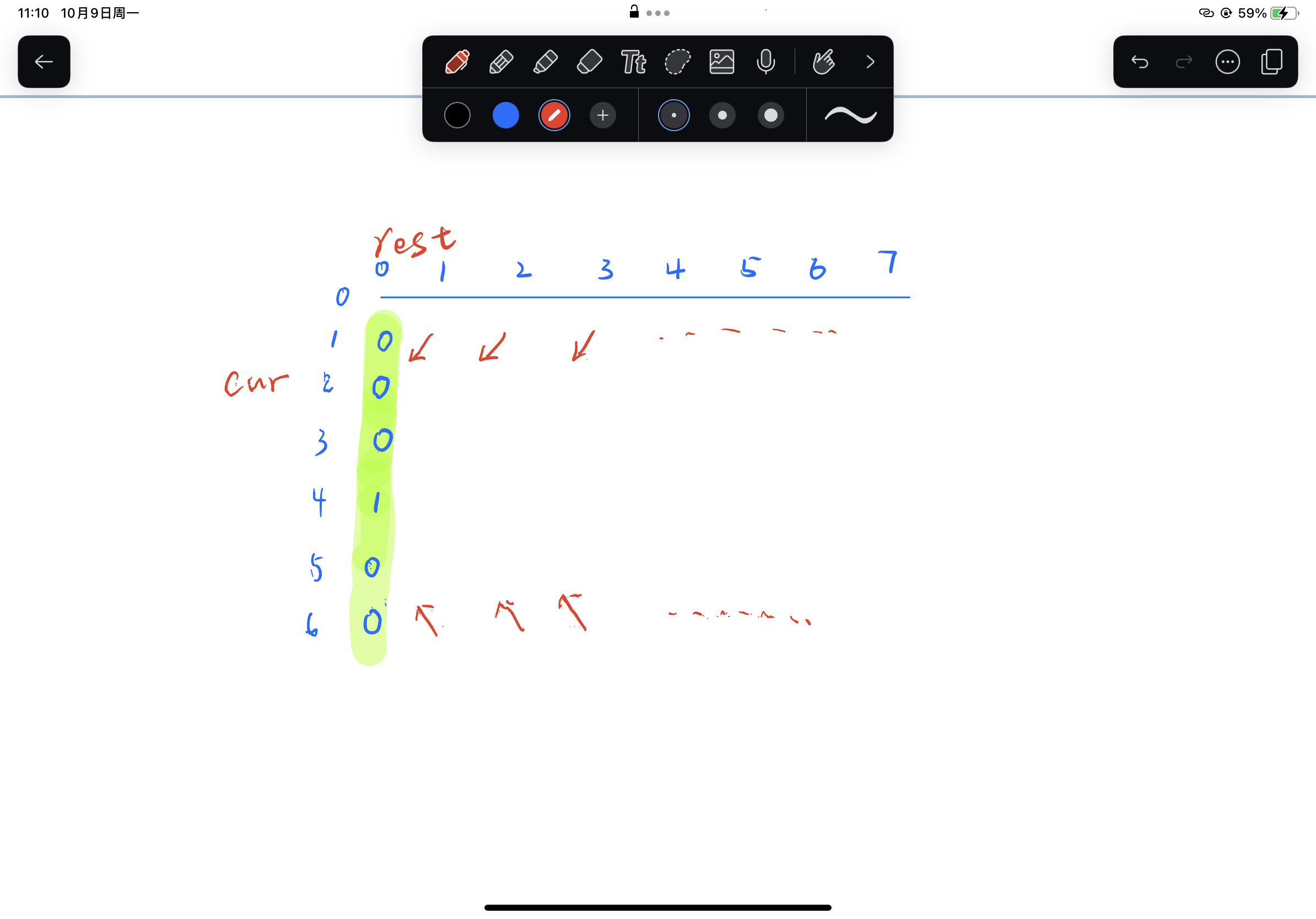
那么我们既然有了第一列的数字 我们就可以推出整个dp数组的数值
从而我们就能得出 当前为start 还有k步要走的时候 我们有几种路径
代码表示如下
int process3(int cur , int rest , int aim , int n)
{vector<vector<int>> dp(n + 1 , vector<int>(rest + 1)); for (int i = 0 ; i < n + 1 ; i++ ) { for (int j = 0; j < rest + 1 ; j++) { dp[i][j] = 0; } } // row 1 dp[aim][0] = 1; for (int r = 1 ; r <= rest ; r++) { dp[1][r] = dp[2][r-1]; for (int c = 2 ; c < n ; c++) { dp[c][r] = dp[c-1][r-1] + dp[c+1][r-1]; } dp[n][r] = dp[n-1][r-1]; } return dp[cur][rest];
}
这就是完整的解决动态规划问题的步骤
先后选牌问题
初级递归
假设现在给你一个数组 长度为N (N > 0) 数组内部储存着int类型的值 大小为(1~100)
现在两个人先后选数字 有如下规定
- 只能选择最边界的数字
- 如果这个数字被选择了 则从数组中移除
那么我们其实可以写出先选和后选两个函数
一开始我们写出的递归函数如下
int f(vector<int>& arr , int L , int R)
int g(vector<int>& arr , int L , int R)
这里两个函数的意义分别是
- f优先选择的最大值
- g后手选择的最大值
参数的含义是
- arr 数组
- L 左边界
- R 右边界
代码表示如下
int f(vector<int>& arr , int L , int R)
{ if (L == R) { return arr[L]; } int p1 = arr[L] + g(arr , L + 1 , R ); int p2 = arr[R] + g(arr , L , R - 1); return max(p1 , p2);
} int g(vector<int>& arr , int L , int R)
{ if (L == R) { return 0; } int p1 = f(arr , L + 1 , R);int p2 = f(arr , L , R -1);return min(p1 , p2);
}
这里解释下为什么g函数中要取最小值
因为先手的人可能会拿走L或者R 给我们造成p1 或者 p2两种结果
因为先手的人要赢 所以说只可能会给我们最差的一种结果 所以一定会是较小的那个值
初级动态规划
这里变化的参数实际上就只有左边界和右边界
我们就可以围绕着这两个边界来建表
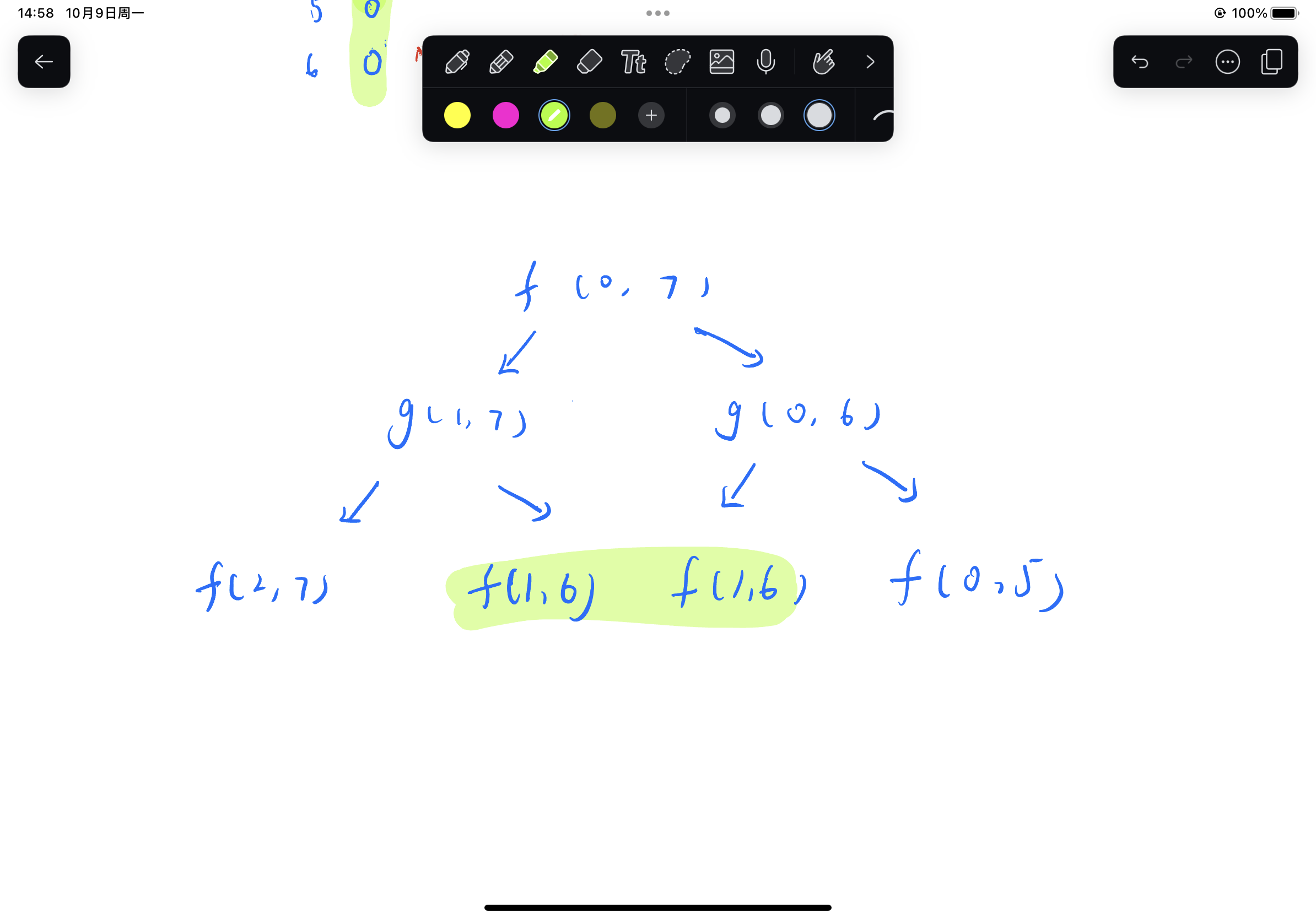
如果按照函数的依赖关系展开 我们很快就会发现重复项
所以说我们要围绕着重复项建表来达到动态规划的效果
而由于这里有两个函数 f 和 g 所以说 我们要建立两张表
我们以为L为横坐标 R为纵坐标建立两张表
L和R的范围是1 ~ R+1
代码表示如下
int _f2(vector<int>& arr , int L , int R , vector<vector<int>>& fmap , vector<vector<int>>& gmap)
{ if (fmap[L][R] != 0) { return fmap[L][R]; } int ans = 0; if ( L == R) { ans = arr[L]; } else { int p1 = arr[L] + _g2(arr , L+1 , R , fmap , gmap); int p2 = arr[R] + _g2(arr , L , R-1 , fmap , gmap); ans = max(p1 , p2); } fmap[L][R] = ans; return ans; }
int _g2(vector<int>& arr , int L , int R , vector<vector<int>>& fmap , vector<vector<int>>& gmap)
{ if (gmap[L][R] != 0){return gmap[L][R];}int ans = 0;if (L == R){ ans = 0;} else { int p1 = _f2(arr , L , R -1 , fmap , gmap);int p2 = _f2(arr , L + 1 , R , fmap , gmap);ans = min(p1 , p2);} gmap[L][R] = ans;return ans;
}动态规划
我们以L为横坐标 R为纵坐标画一个gmap图 并且将L == R的时候的值填入图中
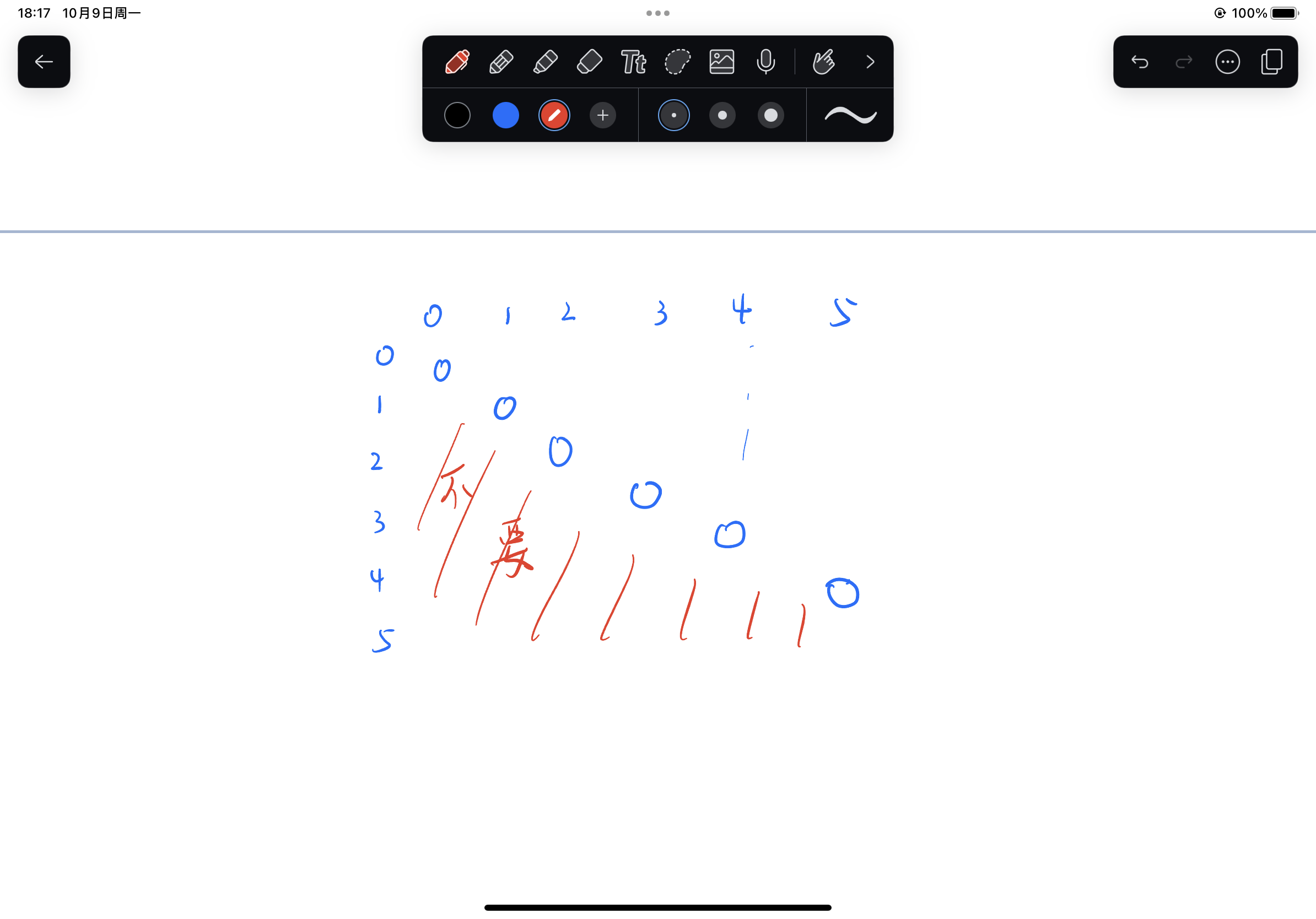
我们可以发现该图的左下角我们是不需要的因为L不可能大于R
那么我们的gmap上右上角的随机一点是依赖于什么呢?
回归到我们最初的递归方程中
_f2(arr , L , R -1 , fmap , gmap);
_f2(arr , L + 1 , R , fmap , gmap);
我们可以发现是依赖于fmap的 L R-1 以及 L+1 R
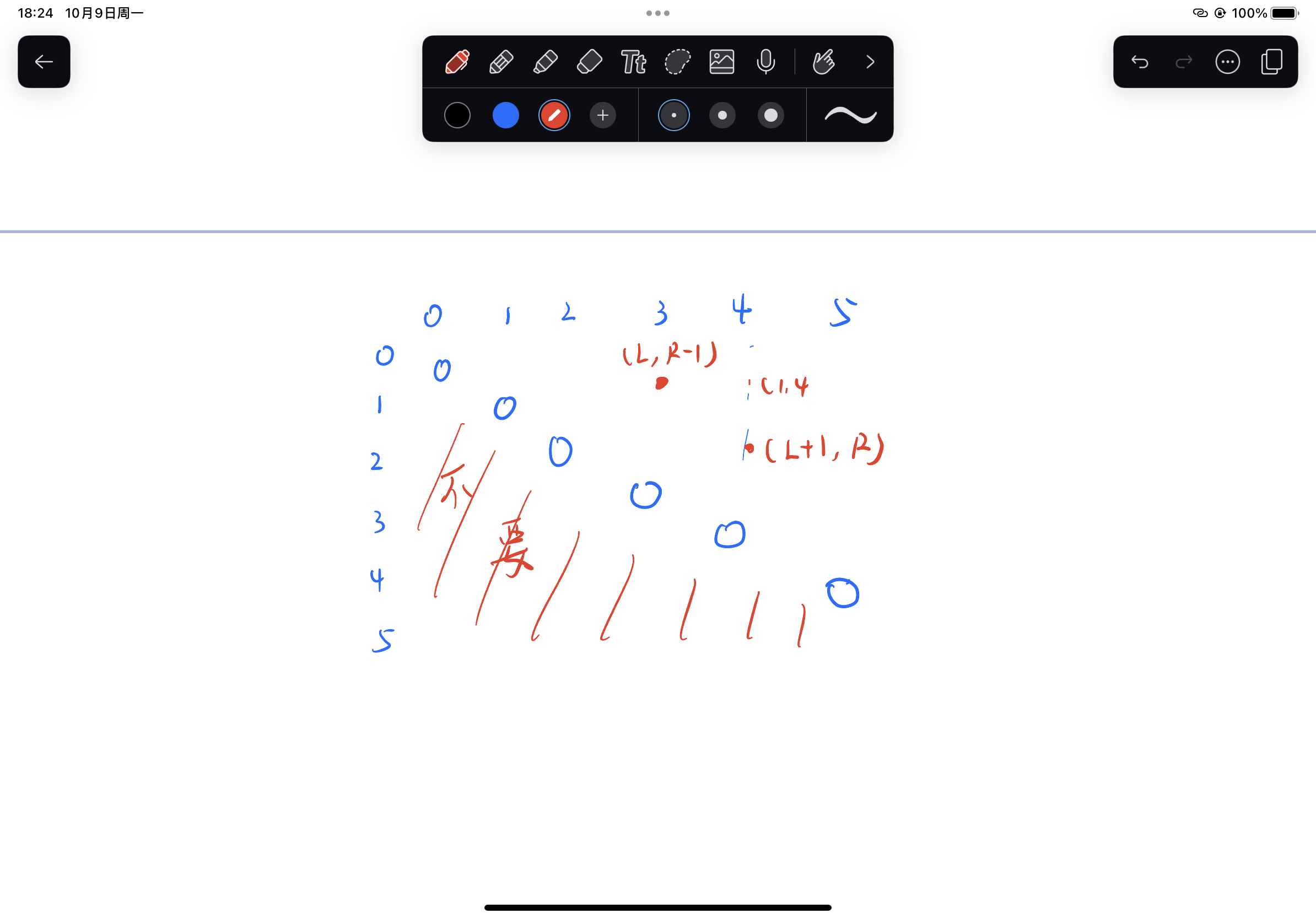
如果映射到fmap中 我们可以发现刚好是斜对角线上的两点 既然我们现在知道了斜对角线上的值 我们现在就可以开始填写这两张map表了
代码表示如下
int f3(vector<int>& arr , int L , int R)
{vector<vector<int>> fmap( R + 1, vector<int>(R+1));for (int i = 0 ; i < R + 1 ; i++){for (int j = 0; j < R + 1 ; j++){fmap[i][j] = 0;if (i == j){fmap[i][j] = arr[i];}}}vector<vector<int>> gmap( R+1 , vector<int>(R+1));for (int i = 0 ; i < R + 1 ; i++){for (int j = 0; j < R + 1 ; j++){gmap[i][j] = 0;}} for (int startcol = 1 ; startcol < R + 1; startcol++ ){int col = startcol;int row = 0;while (col < R + 1){fmap[row][col] = max(gmap[row][col-1] + arr[row] , gmap[row+1][col] + arr[col]);gmap[row][col] = min(fmap[row][col-1] , fmap[row+1][col]);row++;col++;}}return fmap[L][R];
}其实最关键的代码就是这两行
fmap[row][col] = max(gmap[row][col-1] + arr[col] , gmap[row+1][col] + arr[row]);gmap[row][col] = min(fmap[row][col-1] , fmap[row+1][col]);
我们可以发现 这其实就是将原来代码中的函数
int p1 = arr[L] + _g2(arr , L+1 , R , fmap , gmap); int p2 = arr[R] + _g2(arr , L , R-1 , fmap , gmap); ans = max(p1 , p2);
变成了表中的数字相加
这就是动态规划的一般套路
相关文章:

【Hello Algorithm】暴力递归到动态规划(一)
暴力递归到动态规划(一) 斐波那契数列的动态规划机器人走路初级递归初级动态规划动态规划 先后选牌问题初级递归初级动态规划动态规划 我们可以一句话总结下动态规划 动态规划本质是一种以空间换时间的行为 如果你发现有重复调用的过程 在经过一次之后把…...
凉鞋的 Godot 笔记 107. 脚本窗口文件系统窗口
107. 脚本窗口&文件系统窗口 在上一篇,我们完成了第二轮循环,同时也接触了一些新内容,如下所示: 频率使用比较高的窗口,还剩下最后两个了,一个是脚本窗口: 另一个是文件系统窗口: 脚本窗口 和 文件系统…...

数据源作用以及spring配置数据源
数据源 数据源,简单理解为数据源头,提供了应用程序所需要数据的位置。数据源保证了应用程序与目标数据之间交互的规范和协议,它可以是数据库,文件系统等等。其中数据源定义了位置信息,用户验证信息和交互时所需的一些…...

Javaweb中的servlet中的消息体是什么?
2023年10月9日,周一晚上 目录 什么是消息体 什么是HTTP响应 HTTP响应由谁产生,发给谁 响应头具体有什么内容 Content-Type的值怎么写 HTTP响应例子 什么是消息体 消息体(message body)指HTTP响应中的实体主体内容。 什么是HTTP响应 在HTTP响应中…...
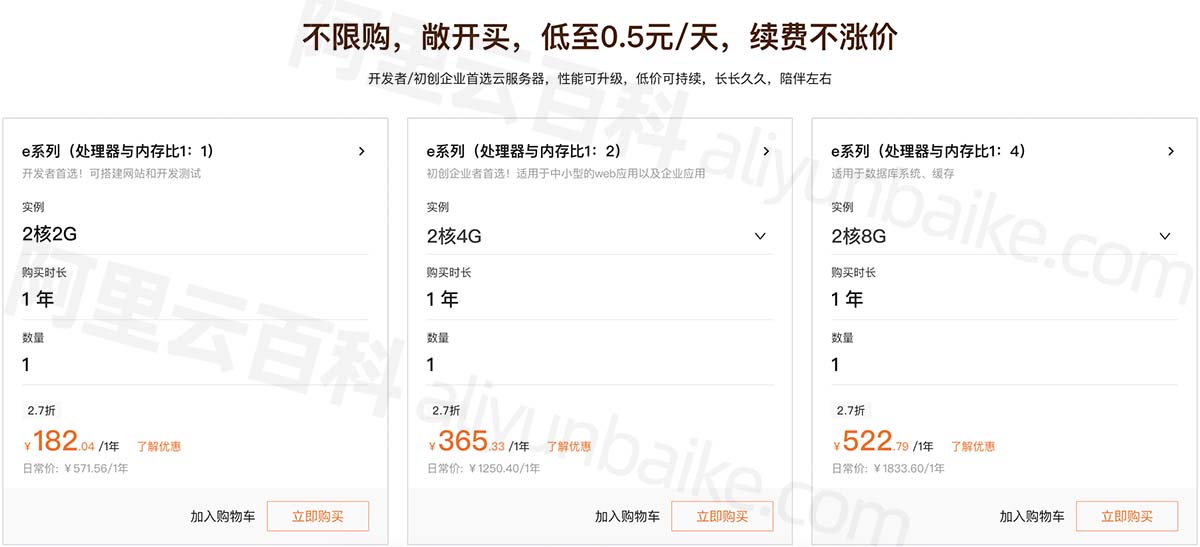
饥荒服务器阿里云租用价格表一年和一个月收费报价表
饥荒阿里云服务器多少钱一个月?阿里云服务器价格9元一个月,阿里云轻量应用服务器2核2G3M带宽轻量服务器一年108元,2核4G4M带宽轻量服务器一年297.98元12个月;阿里云ECS云服务器e系列2核2G配置182元一年、2核4G配置365元一年、2核8…...

前端 JS 经典:Math 常用方法汇总
1. Math.ceil 向上取整 Math.ceil(1.2) // 2 2. Math.floor 向下取整 Math.floor(1.2) // 1 3. Math.round 四舍五入 Math.round(1.4) // 1 Math.round(1.6) // 2 4. Math.random 0-1 随机数 Math.random() // 0.2745798547204079 5. Math.max 返回大值 Math.max(1.2,…...

MongoDB 笔记
1 insert 、create、save区别 insert: 主键不存在则正常插入;主键已存在,抛出DuplicateKeyException 异常 save: 主键不存在则正常插入;主键已存在则更新 insertMany:批量插入,等同于批量执行 insert create&#x…...
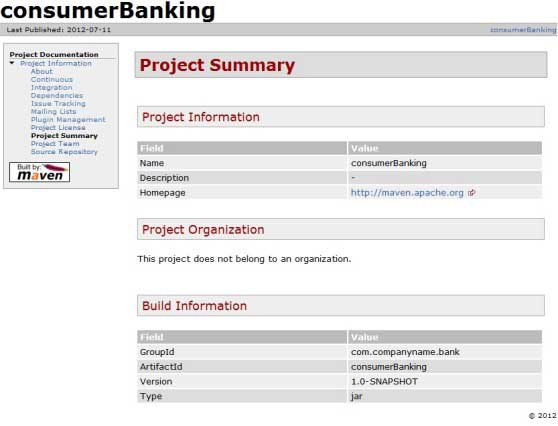
Maven 项目文档
本章节我们主要学习如何创建 Maven 项目文档。 比如我们在 C:/MVN 目录下,创建了 consumerBanking 项目,Maven 使用下面的命令来快速创建 java 项目: mvn archetype:generate -DgroupIdcom.companyname.bank -DartifactIdconsumerBanking -…...
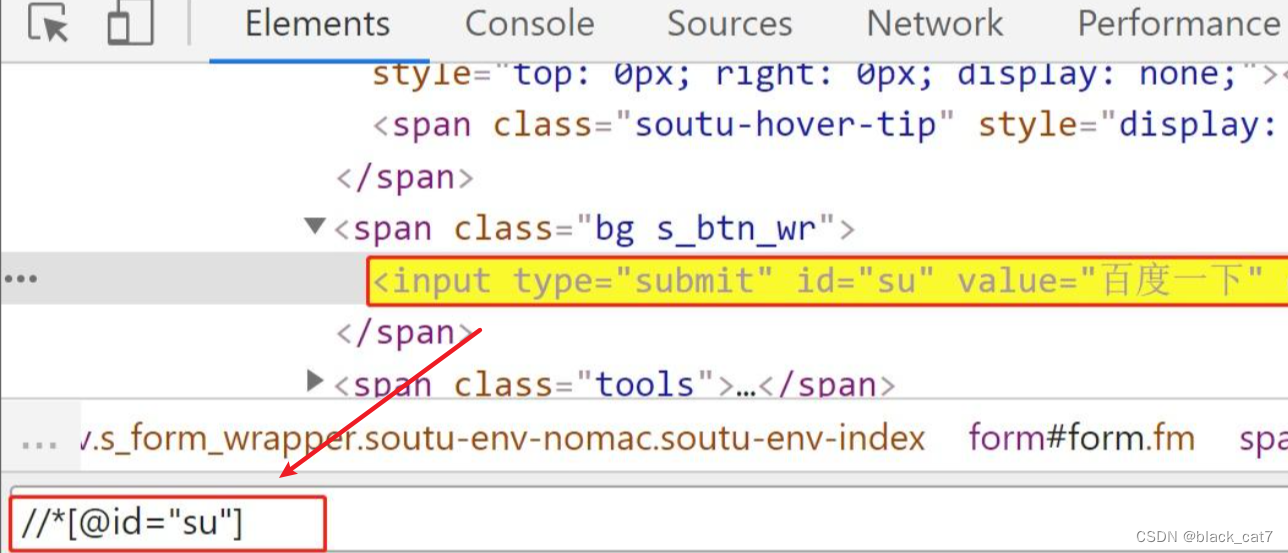
浏览器中XPath的使用
概念 XPath (XML Path Language) 是一门在 XML 文档中查找信息的语言,可用来在 XML 文档中对元素和属性进行遍历。 XPath定位在爬虫和自动化测试中都比较常用,通过使用路径表达式来选取 XML 文档中的节点或者节点集,熟练掌握XPath可以极大提…...

js录制屏幕并输出视频
借助navigator,需要注意的是navigator.mediaDevices.getDisplayMedia需要在https使用,若部署环境为http,则会导致navigator.mediaDevices.getDisplayMedia为undefined 参数中的name为输出视频的文件名 time为录制的时长,若时长为一秒则time值…...

华为OD机试 - 数组组成的最小数字(Java 2023 B卷 100分)
目录 专栏导读一、题目描述二、输入描述三、输出描述四、解题思路五、Java算法源码六、效果展示1、输入2、输出3、说明 华为OD机试 2023B卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试(JAVA)真题(A卷B卷&#…...

数据结构-顺序存储二叉树
文章目录 目录 文章目录 前言 一 . 什么是顺序存储二叉树 二 . 模拟实现 前序遍历 总结 前言 大家好,今天给大家讲一下顺序存储二叉树 一 . 什么是顺序存储二叉树 顺序存储二叉树是一种将二叉树的节点按照从上到下、从左到右的顺序存储在数组中的方法。具体来说,顺…...
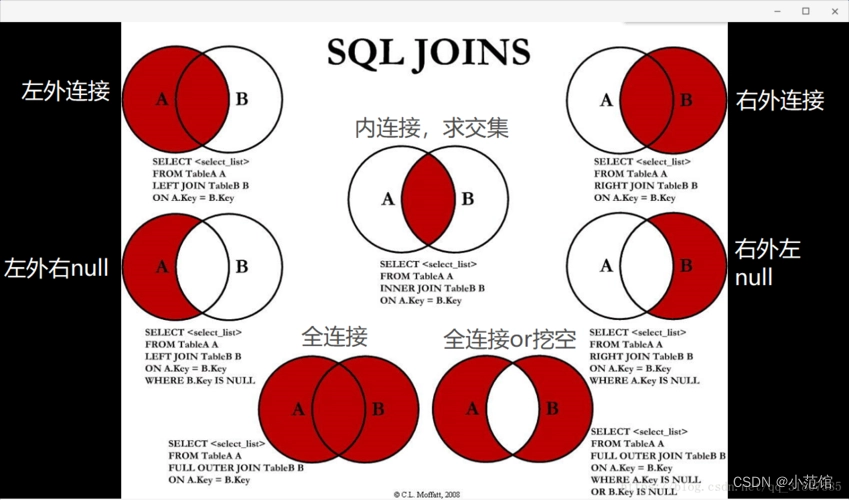
mysql学习实践
这里写目录标题 查找重复数据查找重复数据的字段值以及重复的次数如果你只想查找重复数据,而不需要知道重复的次数,可以简化查询如下 根据某个字段查询重复的数据,并取id最大的那条数据(用于商机列表展示)将逗号分隔的…...

键盘控制应用--通过键盘发送控制指令
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理 文章目录 系列文章目录前言代码原理实现前言 认知有限,望大家多多包涵,有什么问题也希望能够与大家多交流,共同成长! 本文先对键盘控制应用做个简单的介绍,具体内容后…...

python中pytorch的广播机制——Broadcasting
广播机制 numpy 在算术运算期间采用“广播”来处理具有不同形状的 array ,即将较小的阵列在较大的阵列上“广播”,以便它们具有兼容的形状。Broadcasting是一种没有copy数据的expand 不过两个维度不相同,在前面插入维度1扩张维度1到相同的维…...

基于BES平台音乐信号处理之DRC算法实现
基于BES平台音乐信号处理之DRC算法实现 是否需要申请加入数字音频系统研究开发交流答疑群(课题组)?加我微信hezkz17, 本群提供音频技术答疑服务 1 DRC实现 drc.h 2 调用 audio_process.c 3 DRC动态范围控制算法在音乐信号处理中的位置 4 DRC具体细节源码 可参考…...

如何加快香山处理器Chisel->Verilog编译速度
graalvm installation 更换JVM。我们推荐使用GraalVM代替OpenJDK。 使用GraalVM免费版作为JVM编译香山比OpenJDK快10%-20%。 -------------------------------------------------------------------------- https://www.graalvm.org/latest/docs/getting-started/linux/ downl…...
pillow篇---pillow连续打开同一张图片会导致打开失败问题
如果你需要在多次操作同一张图像时避免出现缓存问题,你可以使用 Image.open() 方法的 seek() 方法将文件指针移动到图像数据的开头,以便重新读取图像数据。示例如下: from PIL import Image# 打开图像文件 image Image.open(example.jpg)# …...
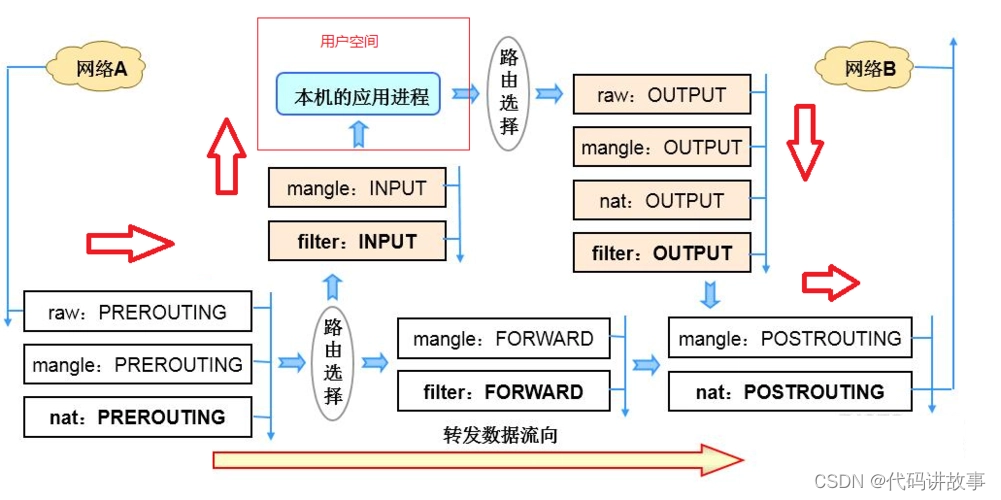
详细解说iptables 高阶用法,用来完成哪些高效率网络路由策略场景,iptables 实现域名过滤,Linux如何利用iptables屏蔽某些域名?
详细解说iptables 高阶用法,用来完成哪些高效率网络路由策略场景,iptables 实现域名过滤,Linux如何利用iptables屏蔽某些域名? Linux利用iptables屏蔽某些域名 以下规则是屏蔽以 youtube.com 为主的所有一级 二级 三级等域名。 iptables -A OUTPUT -m string --string &qu…...

面试总结-Redis篇章(十二)——Redis是单线程的,为什么还那么快
Redis是单线程的,为什么还那么快 Redis是单线程的,为什么还那么快什么是IO多路复用 阻塞IO非阻塞IOIO多路复用 Redis是单线程的,为什么还那么快 Redis是纯内存操作,执行速度非常快采用单线程,避免不必要的上下文切换可…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
