2731. 移动机器人
2731. 移动机器人有一些机器人分布在一条无限长的数轴上,他们初始坐标用一个下标从 0 开始的整数数组 nums 表示。当你给机器人下达命令时,它们以每秒钟一单位的速度开始移动。
给你一个字符串 s ,每个字符按顺序分别表示每个机器人移动的方向。'L' 表示机器人往左或者数轴的负方向移动,'R' 表示机器人往右或者数轴的正方向移动。
当两个机器人相撞时,它们开始沿着原本相反的方向移动。
请你返回指令重复执行 d 秒后,所有机器人之间两两距离之和。由于答案可能很大,请你将答案对 109 + 7 取余后返回。
注意:
- 对于坐标在
i和j的两个机器人,(i,j)和(j,i)视为相同的坐标对。也就是说,机器人视为无差别的。 - 当机器人相撞时,它们 立即改变 它们的前进方向,这个过程不消耗任何时间。
-
当两个机器人在同一时刻占据相同的位置时,就会相撞。
-
例如,如果一个机器人位于位置 0 并往右移动,另一个机器人位于位置 2 并往左移动,下一秒,它们都将占据位置 1,并改变方向。再下一秒钟后,第一个机器人位于位置 0 并往左移动,而另一个机器人位于位置 2 并往右移动。
-
例如,如果一个机器人位于位置 0 并往右移动,另一个机器人位于位置 1 并往左移动,下一秒,第一个机器人位于位置 0 并往左行驶,而另一个机器人位于位置 1 并往右移动。
-
示例 1:
输入:nums = [-2,0,2], s = "RLL", d = 3 输出:8 解释: 1 秒后,机器人的位置为 [-1,-1,1] 。现在下标为 0 的机器人开始往左移动,下标为 1 的机器人开始往右移动。 2 秒后,机器人的位置为 [-2,0,0] 。现在下标为 1 的机器人开始往左移动,下标为 2 的机器人开始往右移动。 3 秒后,机器人的位置为 [-3,-1,1] 。 下标为 0 和 1 的机器人之间距离为 abs(-3 - (-1)) = 2 。 下标为 0 和 2 的机器人之间的距离为 abs(-3 - 1) = 4 。 下标为 1 和 2 的机器人之间的距离为 abs(-1 - 1) = 2 。 所有机器人对之间的总距离为 2 + 4 + 2 = 8 。
示例 2:
输入:nums = [1,0], s = "RL", d = 2 输出:5 解释: 1 秒后,机器人的位置为 [2,-1] 。 2 秒后,机器人的位置为 [3,-2] 。 两个机器人的距离为 abs(-2 - 3) = 5 。
提示:
2 <= nums.length <= 105-2 * 109 <= nums[i] <= 2 * 1090 <= d <= 109nums.length == s.lengths只包含'L'和'R'。nums[i]互不相同。
题解:
当两个机器人相撞时,它们会沿着原本相反的方向移动。由于机器人之间并没有任何区别,相撞可以看做是穿透,原本左边的机器人相撞后交换为右边的机器人,原本右边的机器人相撞后交换为左边的机器人,这样一来,两个机器人仿佛没有相撞过。因此,我们可以无视相撞,独立计算每个机器人 ddd 秒后所处的位置。
总结三点:
- 碰撞是障眼法, 可以看做穿透
- 排序+前缀和计算距离和。
- 求模时求一次和多次没啥区别,可能减少遗漏
概率中的排列组合的思想,考虑一共有多少区间会包括pos[i] - pos[i - 1]这段距离,左边界有i种可能,右边界有(n-i)种可能,两个相乘就是区间的组合数量:i*(n-i)。区间组合数量乘上距离就是这段距离(pos[i] - pos[i - 1])产生的总距离,枚举所有i就是所有距离段的和。
code:
class Solution {static final int MOD = 1000000007;public int sumDistance(int[] nums, String s, int d) {int n = nums.length;long[] pos = new long[n];for (int i = 0; i < n; i++) {if (s.charAt(i) == 'L') {pos[i] = (long) nums[i] - d;} else {pos[i] = (long) nums[i] + d;}}Arrays.sort(pos);long res = 0;for (int i = 1; i < n; i++) {res += 1L * (pos[i] - pos[i - 1]) * i % MOD * (n - i) % MOD;res %= MOD;}return (int) res;}
}相关文章:

2731. 移动机器人
2731. 移动机器人有一些机器人分布在一条无限长的数轴上,他们初始坐标用一个下标从 0 开始的整数数组 nums 表示。当你给机器人下达命令时,它们以每秒钟一单位的速度开始移动。 给你一个字符串 s ,每个字符按顺序分别表示每个机器人移动的方…...

小程序实现人脸识别功能
调用api wx.startFacialRecognitionVerify 第一步: // 修改方法expertUpdate() {wx.startFacialRecognitionVerify({name: _this.registerForm.realName, //身份证名称idCardNumber: _this.registerForm.idCard, //身份证号码checkAliveType: 1, //屏幕闪烁(人脸核验的交互…...

【】javax.crypto.IllegalBlockSizeException: Input length not multiple of 8 bytes
问题描述 jdk版本:8 用DES进行加解密,其中转换模式为“DES/CBC/NoPadding”,要加密的明文为 “密码学浅析”,执行加密操作,报如下错误 Exception in thread "main" javax.crypto.IllegalBlockSizeExcepti…...
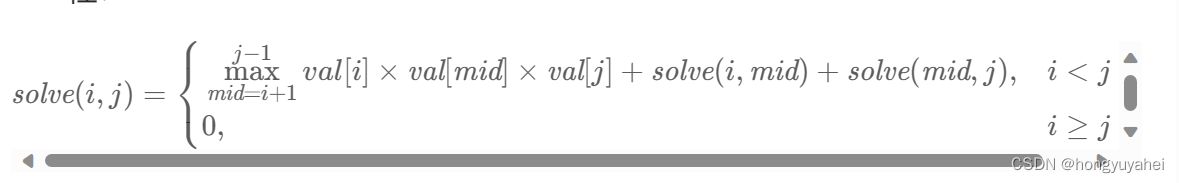
312.戳气球
将戳气球转换到添加气球,记忆搜索slove(i,j):在开区间(i,j)全部填满气球得到的最多硬币数,两端val[i]、val[j] class Solution { public:vector<vector<int>> ans;vector<int> val;int slove(int left,int right){if(left&…...

get_trade_detail_data函数使用
查阅股票持仓情况 positions get_trade_detail_data(‘8000000213’, ‘stock’, ‘position’) for dt in positions: print(f’股票代码: {dt.m_strInstrumentID}, 市场类型: {dt.m_strExchangeID}, 证券名称: {dt.m_strInstrumentName}, 持仓量: {dt.m_nVolume}, 可用数量:…...
【融合ChatGPT等AI模型】Python-GEE遥感云大数据分析、管理与可视化及多领域案例实践应用
目录 第一章 理论基础 第二章 开发环境搭建 第三章 遥感大数据处理基础与ChatGPT等AI模型交互 第四章 典型案例操作实践 第五章 输入输出及数据资产高效管理 第六章 云端数据论文出版级可视化 更多应用 随着航空、航天、近地空间等多个遥感平台的不断发展,近…...

LeetCode862 和至少为k的最短子数组
题目: 解析: 1、先构造前缀和数组 2、单调队列存放滑动窗口,目的求Sj-Si >k的情况下,窗口最小。 代码: class Solution {public int shortestSubarray(int[] nums, int k) {int n nums.length;long[] sums new …...

网卡bonding模式 - bond模式配置介绍
网卡bonding简介 网卡绑定就是把多张物理网卡通过软件虚拟成一个虚拟的网卡,配置完毕后,所有的物理网卡的ip和mac将会变成相同的。多网卡同时工作可以提高网络速度,还可以实现网卡的负载均衡、冗余。 bonding模式 1 round-robin(mode0) 轮转…...

做了个 chrome 插件实现 B 站视频截图功能,直接从当前视频帧无损复制
起因是看 B 站视频想截个图很麻烦,右下角暂停按钮无法去除,于是写了一行代码把暂停按钮隐藏。 后经提醒,发现可以通过 canvas 获取视频帧来截取图片,于是写了如下代码完美获取视频帧。 var v document.querySelector(".bpx…...

Docker linux 安装
sudo yum update sudo yum clean all sudo yum makecache#安装依赖 sudo yum install -y yum-utils device-mapper-persistent-data lvm2 #添加官方存储库 sudo yum-config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo#安装-跳过一些异常依赖…...
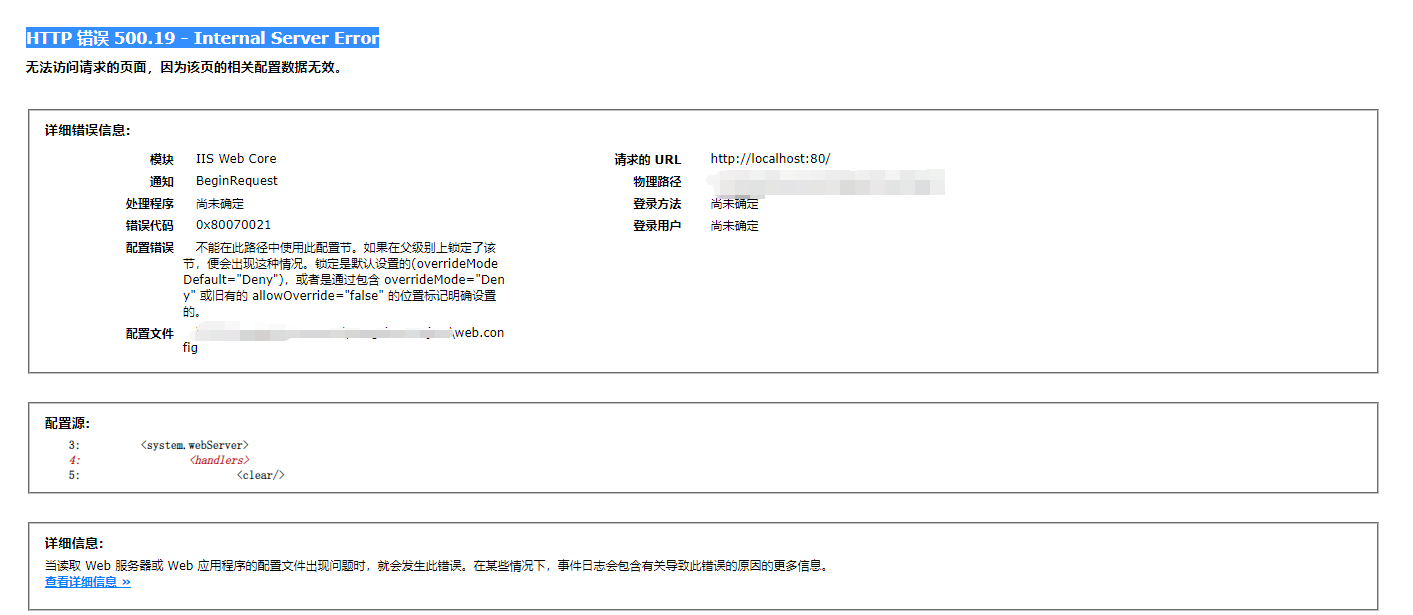
windows部署django服务器
windows部署django服务器 1、安装IIS1.1 控制面板-----程序----程序和功能----启用或关闭windows功能1.2安装IIS服务器,完成后,重新进入,把CGI安装进系统 2、安装python与虚拟环境2.1 安装python2.2 安装virtualenv虚拟环境2.3 创建一个虚拟环…...

ChatGPT prompt汇总-个人使用-持续更新....
用途 学术写作更新记录 学术写作 中译英(GPT-4) I am a researcher studying deep learning and now trying to revise my manuscript which will be submitted to the Journal of Nature . I want you to act as a scientific English-Chinese translator, I will provide yo…...
Vue实现简单的接口封装
1. 在src中创建一个api文件夹 2. 按功能、模块等新建对应的js文件 3. 在内部写对应的封装接口,并导出 import axios from "axios";/*** 接口名称:* 接收参数:* 返回参数:* */export const miens ()>{return new P…...

软件测试工具有什么作用?有哪些好用的测试工具推荐?
软件测试工具是现代软件测试中不可或缺的重要组成部分,指的是一系列在软件开发过程中使用的工具,用于帮助测试人员进行测试活动,提高测试效率,减少测试成本。选择并使用合适的软件测试工具,可提高软件质量和效率。 一…...
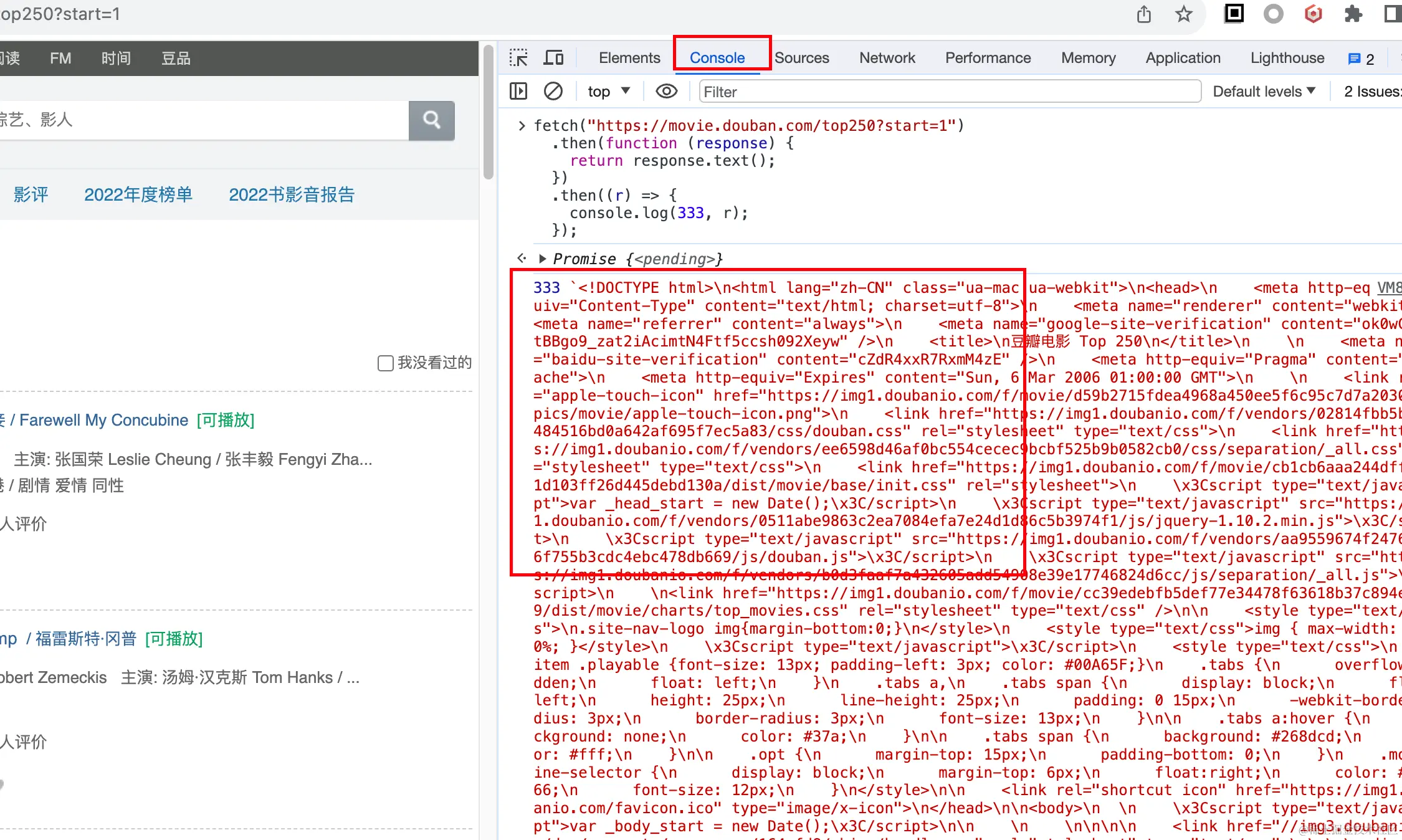
写爬虫?前端er何必用python
前言 说起网络爬虫,很多人第一时间想到python,但爬虫并非只能用python实现,虽然网上大部分爬虫文章都在说python爬虫,但对于前端程序员来说,我觉得js才是最屌的(对于简单爬取任务来说,复杂的我暂时没碰到~),下面说说我的经验(是的,仅限本人经验),希望能给各位前…...

交通物流模型 | 基于交通图卷积长短时记忆网络的网络级交通流预测
交通物流模型 | 基于交通图卷积长短时记忆网络的网络级交通流预测 由于道路网络时变的交通模式和复杂的空间依赖性,交通流预测是一个具有挑战性的时空预测问题。为了克服该挑战,作者将交通网络看为一张图,并提出一个新的深度学习预测模型,交通图卷积长短时记忆网络(TGC-L…...

web 基础和http 协议
一、域名 域名的概念 IP地址不易记忆,域名方便记住,以便于用户进行搜索访问 早期使用Hosts文件解析域名地址 缺点: ① 主机名称重复 ② 主机维护困难 DNS(Domain Name System)域名系统 ① 分布式 将一个大的数…...

Java常量与变量
Java常量与变量 在程序执行过程中,其值不能被改变的量称为常量,其值能被改变的量称为变量。 Java关键字 Java关键字 int public (公有的,可跨包) new finally throw (抛出一个异常对象) continuefloatlongshort extends (继承,用于类继承类) returnbrea…...
神经网络中卷积和池化的区别
1、什么叫卷积? 卷积层是用一个固定大小的矩形区去席卷原始数据,将原始数据分成一个个和卷积核大小相同的小块,然后将这些小块和卷积核相乘输出一个卷积值(注意这里是一个单独的值,不再是矩阵了)。 卷积的…...

RK3568平台开发系列讲解(驱动篇)RK3568 PWM详解
🚀返回专栏总目录 文章目录 一、什么是PWM二、RK3568 PWM2.1、PWM 通道与引脚2.2、PWM 简介2.3、PWM 设备节点沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 PWM 是很常用到功能,我们可以通过 PWM 来控制电机速度,也可以使用 PWM 来控制 LCD 的背光亮度。 一、什…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
