[代码学习]einsum详解
einsum详解
该函数用于对一组输入 Tensor 进行 Einstein 求和,该函数目前仅适用于paddle的动态图。
Einstein 求和是一种采用 Einstein 标记法描述的 Tensor 求和,输入单个或多个 Tensor,输出单个 Tensor。

paddle.einsum(equation, *operands)
参数
- equation (str):求和标记
- operands (Tensor, [Tensor, …]):输入 Tensor
返回
- Tensor:输出 Tensor
求和特例
-
单操作数
-
迹:trace
-
对角元:diagonal
-
转置:transpose
-
求和:sum
-
-
双操作数
-
内积:dot
-
外积:outer
-
广播乘积:mul,*
-
矩阵乘:matmul
-
批量矩阵乘:bmm
-
-
多操作数
-
广播乘积:mul,*
-
多矩阵乘:A.matmul(B).matmul(C)
-
关于求和标记的约定
-
维度分量下标:Tensor 的维度分量下标使用英文字母表示,不区分大小写,如’ijk’表示 Tensor 维度分量为 i,j,k
-
下标对应输入操作数:维度下标以`,`分段,按顺序 1-1 对应输入操作数
-
广播维度:省略号`…`表示维度的广播分量,例如,'i…j’表示首末分量除外的维度需进行广播对齐
-
自由标和哑标:输入标记中仅出现一次的下标为自由标,重复出现的下标为哑标,哑标对应的维度分量将被规约消去
-
输出:输出 Tensor 的维度分量既可由输入标记自动推导,也可以用输出标记定制化
-
自动推导输出
- 广播维度分量位于维度向量高维位置,自由标维度分量按字母顺序排序,位于维度向量低纬位置,哑标维度分量不输出
-
定制化输出
-
维度标记中`->`右侧为输出标记
-
若输出包含广播维度,则输出标记需包含`…`
-
输出标记为空时,对输出进行全量求和,返回该标量
-
输出不能包含输入标记中未出现的下标
-
输出下标不可以重复出现
-
哑标出现在输出标记中则自动提升为自由标
-
输出标记中未出现的自由标被降为哑标
-
例子
-
‘…ij, …jk’,该标记中 i,k 为自由标,j 为哑标,输出维度’…ik’
-
‘ij -> i’,i 为自由标,j 为哑标
-
‘…ij, …jk -> …ijk’,i,j,k 均为自由标
-
‘…ij, …jk -> ij’,若输入 Tensor 中的广播维度不为空,则该标记为无效标记
求和规则
Einsum 求和过程理论上等价于如下四步,但实现中实际执行的步骤会有差异。
第一步,维度对齐:将所有标记按字母序排序,按照标记顺序将输入 Tensor 逐一转置、补齐维度,使得处理后的所有 Tensor 其维度标记保持一致
第二步,广播乘积:以维度下标为索引进行广播点乘
第三步,维度规约:将哑标对应的维度分量求和消除
第四步,转置输出:若存在输出标记,则按标记进行转置,否则按广播维度+字母序自由标的顺序转置,返回转之后的 Tensor 作为输出
关于 trace 和 diagonal 的标记约定(待实现功能)
在单个输入 Tensor 的标记中重复出现的下标称为对角标,对角标对应的坐标轴需进行对角化操作,如’i…i’表示需对首尾坐标轴进行对角化
若无输出标记或输出标记中不包含对角标,则对角标对应维度规约为标量,相应维度取消,等价于 trace 操作
若输出标记中包含对角标,则保留对角标维度,等价于 diagonal 操作
实例实践
首先,看一下一维度简单实验:
import paddle# 定义两个输入矩阵
# paddle.seed(102)
# x = paddle.rand([4])
# y = paddle.rand([5])
x = paddle.to_tensor([1,2,], dtype='float32')
y = paddle.to_tensor([3,4,5], dtype='float32')# sum
sum_x = paddle.einsum('i->', x).numpy()# dot
dox_x = paddle.einsum('i,i->', x, x).numpy()# outer
outer_xy = paddle.einsum("i,j->ij", x, y).numpy()print(f"x: {x.numpy()}, shape: {x.shape}")
print(f"y: {y.numpy()}, shape: {y.shape}")
print(f"sum_x: {sum_x}, shape: {sum_x.shape}")
print(f"dox_x: {dox_x}, shape: {dox_x.shape}")
print(f"outer_xy: {outer_xy}, shape: {outer_xy.shape}")
结果输出为:
x: [1. 2.], shape: [2]
y: [3. 4. 5.], shape: [3]
sum_x: 3.0, shape: ()
dox_x: 5.0, shape: ()
outer_xy: [[ 3. 4. 5.][ 6. 8. 10.]], shape: (2, 3)
然后,看一下高纬度的实验:
import paddle# A = paddle.rand([2, 3, 2])
# B = paddle.rand([2, 2, 3])
A = paddle.to_tensor([[[1,2],[1,2],[1,2]], [[1,2],[1,2],[1,2]]], dtype='float32')
B = paddle.to_tensor([[[3,4,5],[3,4,5]], [[3,4,5],[3,4,5]]], dtype='float32')# transpose
transpose_A = paddle.einsum('ijk->kji', A)# batch matrix multiplication
BMM_AB = paddle.einsum('ijk, ikl->ijl', A,B)# Ellipsis transpose
ET_A = paddle.einsum('...jk->...kj', A)# Ellipsis batch matrix multiplication
EBMM_AB = paddle.einsum('...jk, ...kl->...jl', A,B)print(f"A: {A.numpy()}, shape: {A.shape}")
print(f"B: {B.numpy()}, shape: {B.shape}")
print(f"transpose_A: {transpose_A.numpy()}, shape: {transpose_A.shape}")
print(f"BMM_AB: {BMM_AB.numpy()}, shape: {BMM_AB.shape}")
print(f"ET_A: {ET_A.numpy()}, shape: {ET_A.shape}")
print(f"EBMM_AB: {EBMM_AB.numpy()}, shape: {EBMM_AB.shape}")
结果输出为:
A: [[[1. 2.][1. 2.][1. 2.]][[1. 2.][1. 2.][1. 2.]]], shape: [2, 3, 2]
B: [[[3. 4. 5.][3. 4. 5.]][[3. 4. 5.][3. 4. 5.]]], shape: [2, 2, 3]
transpose_A: [[[1. 1.][1. 1.][1. 1.]][[2. 2.][2. 2.][2. 2.]]], shape: [2, 3, 2]
BMM_AB: [[[ 9. 12. 15.][ 9. 12. 15.][ 9. 12. 15.]][[ 9. 12. 15.][ 9. 12. 15.][ 9. 12. 15.]]], shape: [2, 3, 3]
ET_A: [[[1. 1. 1.][2. 2. 2.]][[1. 1. 1.][2. 2. 2.]]], shape: [2, 2, 3]
EBMM_AB: [[[ 9. 12. 15.][ 9. 12. 15.][ 9. 12. 15.]][[ 9. 12. 15.][ 9. 12. 15.][ 9. 12. 15.]]], shape: [2, 3, 3]
reference
关于matmul可以查看:https://blog.csdn.net/orDream/article/details/133744368
官方链接:
@misc{BibEntry2023Oct,
title = {{einsum-API文档-PaddlePaddle深度学习平台}},
year = {2023},
month = oct,
urldate = {2023-10-10},
language = {chinese},
note = {[Online; accessed 10. Oct. 2023]},
url = {https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/einsum_cn.html}
}
相关文章:

[代码学习]einsum详解
einsum详解 该函数用于对一组输入 Tensor 进行 Einstein 求和,该函数目前仅适用于paddle的动态图。 Einstein 求和是一种采用 Einstein 标记法描述的 Tensor 求和,输入单个或多个 Tensor,输出单个 Tensor。 paddle.einsum(equation, *opera…...

女性必看——“黄体破裂”到底有多可怕?
前几天的亚运会上发生了这样一件事: 雅思敏(化名)是一名国外皮划艇运动员,在亚运会上奋力完成皮划艇比赛后,突然开始 剧烈腹痛、面色苍白,大汗淋漓,经过进一步检查,确诊卵巢黄体破裂…...
colab切换目录的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
基于SSM的生活缴费系统的设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...

【WebLogic】WebLogic 2023年7月补丁导致JVM崩溃的解决方案
受影响版本: Oracle WebLogic 12c(12.2.1.4.0)Oracle WebLogic 14c(14.1.1.0.0) 问题描述: Oracle官方在2023年7月发布的最新版本的OPatch(13.9.4.2.13)存在一个新出现的Bug&#…...

简单OpenSL ES学习
初识OpenSL ES OpenSL ESObjects和Interfaces 所有的Object在OpenSl里面我们拿到的都是一个SLObjectItf:SLObjectItf_创建引擎创建过程要设计得这么麻烦?(object的生命周期)这么多参数,参数类型这么多学习障碍太大&…...
)
Linux网络编程- struct packet_mreq setsockopt()
struct packet_mreq struct packet_mreq 是一个数据结构,用于 Linux 中的原始数据包套接字,当我们想改变套接字的行为以接收特定类型的数据包时,它与 setsockopt() 函数配合使用。 下面是 struct packet_mreq 的定义: struct p…...
C++学习day4
作业: 1> 思维导图 2> 整理代码 1. 拷贝赋值函数课上代码 //拷贝赋值函数课上代码 #include<iostream> using namespace std;//创建类 class Stu { private://私有的string name;int socer;int *age;//此处注意用到指针类型 public://共有的//无参构…...
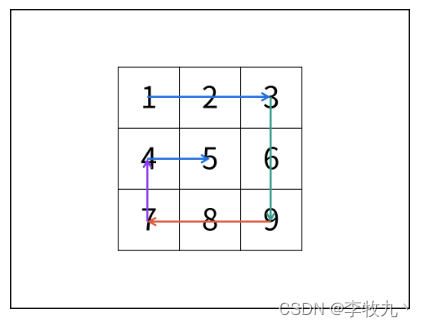
从零学算法54
54.给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 螺旋遍历:从左上角开始,按照 向右、向下、向左、向上 的顺序 依次 提取元素,然后再进入内部一层重复相同的步骤,直到…...
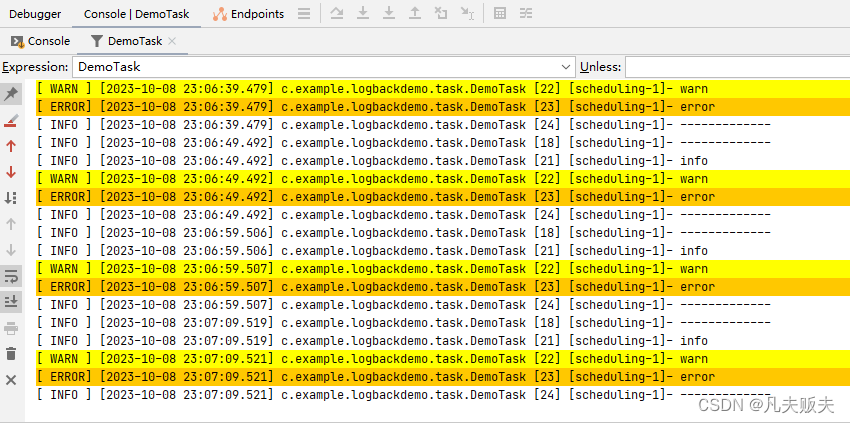
Logback日志框架使用详解以及如何Springboot快速集成
Logback简介 日志系统是用于记录程序的运行过程中产生的运行信息、异常信息等,一般有8个级别,从低到高为All < Trace < Debug < Info < Warn < Error < Fatal < OFF off 最高等级,用于关闭所有日志记录fatal 指出每个…...

Nginx概念
Nginx概念 Nginx 是一款面向性能设计的 HTTP 服务器,相较于 Apache、lighttpd 具有占有内存少,稳定性高等优势,同时也是一个非常高效的反向代理、负载平衡服务器 nginx使用的是反应器模式,主事件循环等待操作系统发出准备事件的信…...
vim基础指令(自用)
这个是自己随便写的,类似于笔记 vim 多模式编辑器 查看指令: gg: 定位光标到最开始行 shift(按)g 定位到最结尾行 nshift(按)g 定位到任意行 shift$ 定位到本行结尾 0 定位到本行开头 w:跨单词移动 h.j.k,l: 左下上右 …...
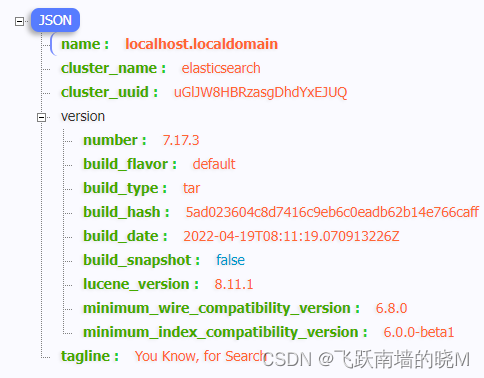
【centos7安装ElasticSearch】
概述 最近工作中有用到ES ,当然少不了自己装一个服务器捣鼓。本文的ElasticSearch 的版本: 7.17.3 一、下载 ElasticSearch 点此下载 下载完成后上传至 Linux 服务器,本文演示放在: /root/ 下,进行解压࿱…...

ElementPlus Switch 开关基础使用
昨天开发用到开关组件 后台返回字段是 can_write 默认是0 or 1 但是Switch 组件绑定的默认值默认是 true or false 直接绑定会导致默认是关闭状态 在页面一加载 值发生变化时 会自己调用 查了文档 需要使用 active-value 和 inactive-value 来指定绑定的数据类型 …...

Spring Boot:自定义注解--annotation
目录 自定义注解的定义和作用范围如何创建自定义注解创建注解接口 如何使用自定义注解进行数据验证创建注解处理器控制器中使用注解 如何为字段添加注解 自定义注解的定义和作用范围 自定义注解可以作用在类、方法、属性、参数、异常、字段或其他注解上。 如何创建自定义注解…...

WIFI频段
问题: 5ghzwifi频段带宽怎么选 智造喵回答: 选择5GHz WiFi频段的带宽取决于你的网络需求和设备兼容性。通常有两种可选的带宽:20MHz和40MHz。 20MHz带宽:这是较为常见的 WiFi 频段带宽设置。它提供较好的穿墙能力和信号稳定性…...

Java的引用详解与示例
引用的作用 在Java中,引用(Reference)是一种重要的概念,它们用于管理对象的生命周期、内存分配和垃圾回收。引用的作用包括以下几个方面: 内存管理:引用帮助Java虚拟机(JVM)管理内存…...
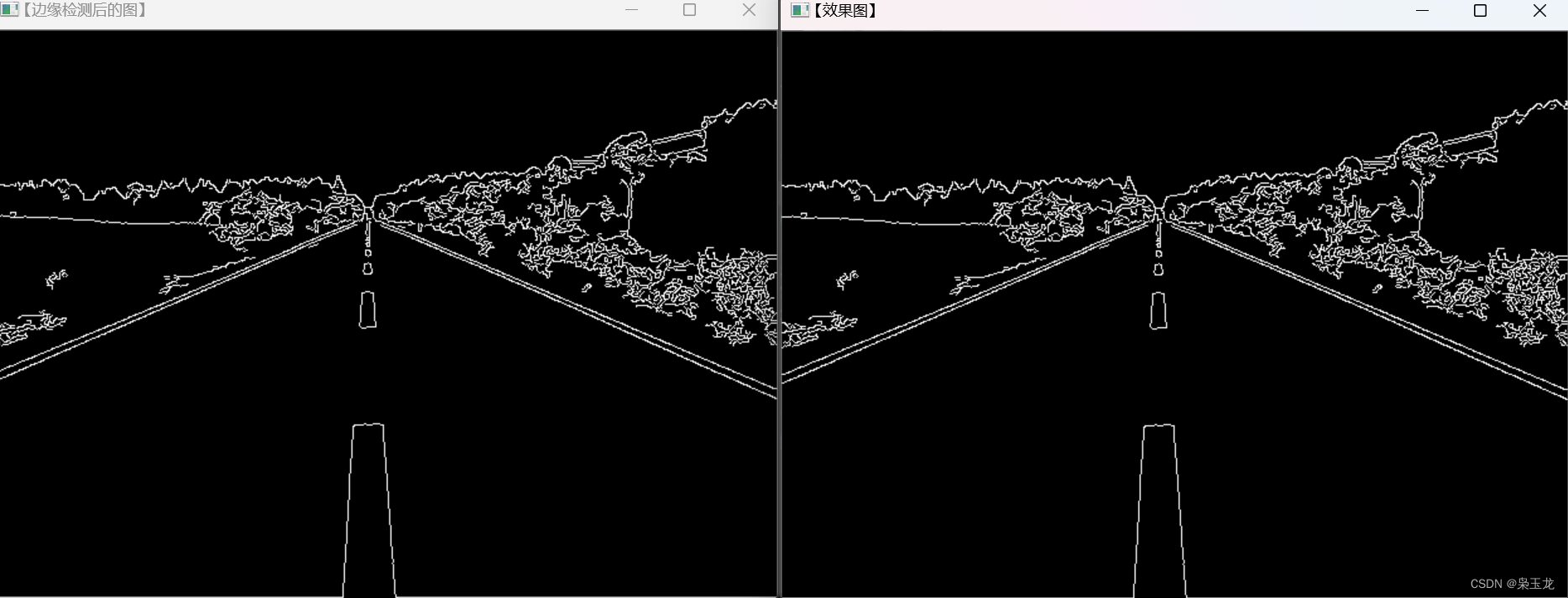
c++视觉处理---霍夫变换
霍夫直线变换的函数 HoughLines 是OpenCV库中用于执行霍夫直线变换的函数。霍夫直线变换用于检测图像中的直线。下面是该函数的基本用法: cv::HoughLines(image, lines, rho, theta, threshold);image: 输入的二值图像,通常是通过边缘检测算法生成的。…...

el-table 边框颜色修改 简单有效!
废话不多说,直接上图 (1)修改前的图如下: 以上是elementUI原组件自带的样式 (2)下面是修改后的边框图如下: 源码如下: <el-table :data"jctableData" border size…...
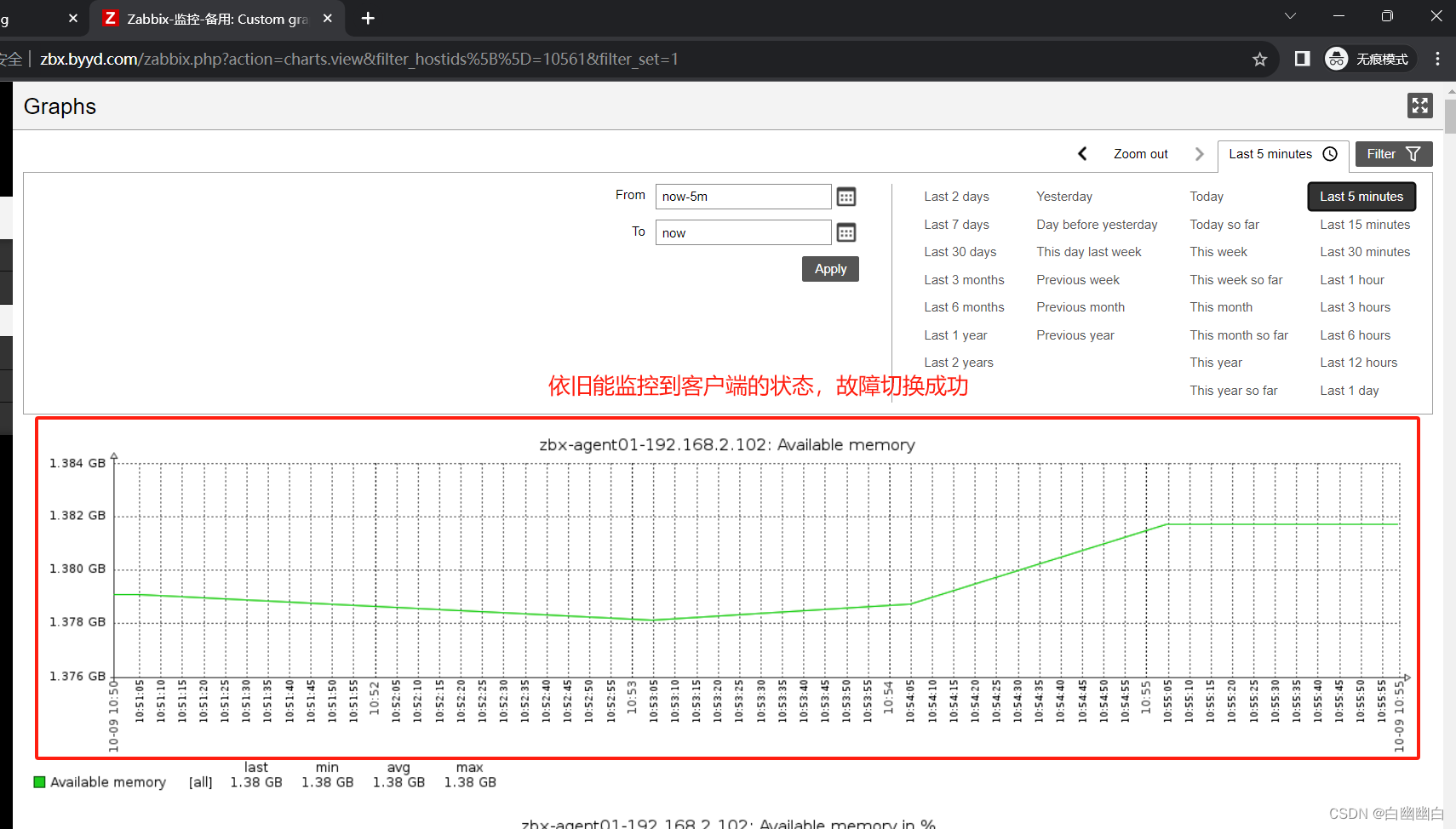
Zabbix第二部分:基于Proxy分布式部署实现Web监控和Zabbix HA集群的搭建
代理和高可用 一、基于zabbix-proxy的分布式监控1.1 分布式监控的作用1.2 数据流向1.3 构成组件 二、部署zabbix代理服务器Step1 前置准备Step2 设置 zabbix 的下载源,安装 zabbix-proxyStep3 部署数据库并将zabbix相关文件导入Step4 修改zabbix-proxy的配置文件&am…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
