学习记忆——数学篇——案例——代数——方程——一元二次方程
重点记忆法
a x 2 + b x + c = 0 ax^2+bx+c=0 ax2+bx+c=0
整体可以由: 根(多少,正负,区间) ⟹ \Longrightarrow ⟹ △ △ △ ⟹ \Longrightarrow ⟹ 求根公式 x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△ ⟹ \Longrightarrow ⟹ 韦达定理 ⟹ \Longrightarrow ⟹ 判断两根符号情况,即根多少由 △ △ △判断,根需要求根公式,求根公式可推导韦达定理,韦达定理可判断两根符号情况。
1.根
⟹ \Longrightarrow ⟹ 根的多少: △ △ △>0,方程有两根, x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△,抛物线与x轴有两个交点 ; △ △ △=0,方程有一根, x x x为 − b 2 a -\frac{b}{2a} −2ab,抛物线与x轴有一个交点; △ △ △<0,方程无根,抛物线与x轴没有交点;
⟹ \Longrightarrow ⟹ 根的正负:两正根( △ ≥ 0 , x 1 + x 2 > 0 , x 1 x 2 > 0 △≥0,x_1+x_2>0,x_1x_2>0 △≥0,x1+x2>0,x1x2>0);两负根( △ ≥ 0 , x 1 + x 2 < 0 , x 1 x 2 > 0 △≥0,x_1+x_2<0,x_1x_2>0 △≥0,x1+x2<0,x1x2>0);异号根( x 1 x 2 < 0 x_1x_2<0 x1x2<0)
⟹ \Longrightarrow ⟹ 根的区间:看顶点(横坐标相当于看对称轴,纵坐标相当于看 △ △ △)、看端点(根所分布区问的端点)。or画图+三要素, △ △ △、对称轴和端点代入。
⟹ \Longrightarrow ⟹ 根与系数关系: x 1 + x 2 = − b a x_1+x_2=-\frac{b}{a} x1+x2=−ab, x 1 ⋅ x 2 = c a x_1·x_2=\frac{c}{a} x1⋅x2=ac。
2. △ △ △判别式
⟹ \Longrightarrow ⟹ b 2 − 4 a c b^2-4ac b2−4ac
⟹ \Longrightarrow ⟹ △ △ △>0,方程有两根, x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△,抛物线与x轴有两个交点
⟹ \Longrightarrow ⟹ △ △ △=0,方程有一根, x x x为 − b 2 a -\frac{b}{2a} −2ab,抛物线与x轴有一个交点
⟹ \Longrightarrow ⟹ △ △ △<0,方程无根,抛物线与x轴没有交点
⟹ \Longrightarrow ⟹ y y y的最值为 4 a c − b 2 4 a \frac{4ac-b^2}{4a} 4a4ac−b2 = -△ 4 a \frac{-△}{4a} 4a-△
⟹ \Longrightarrow ⟹ 弦长公式为 △ ∣ a ∣ \frac{\sqrt{△}}{|a|} ∣a∣△
⟹ \Longrightarrow ⟹ 顶点△面积为 ( △ ) 3 8 a 2 \frac{(\sqrt{△})^3}{8a^2} 8a2(△)3
3.求根公式
x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△
⟹ \Longrightarrow ⟹ 韦达定理为 x 1 + x 2 = − b + △ 2 a + − b − △ 2 a = − b a x_1+x_2=\frac{-b+\sqrt{△}}{2a}+\frac{-b-\sqrt{△}}{2a}=-\frac{b}{a} x1+x2=2a−b+△+2a−b−△=−ab
⟹ \Longrightarrow ⟹ 韦达定理为 x 1 ⋅ x 2 = − b + b 2 − 4 a c 2 a ∗ − b − b 2 − 4 a c 2 a = c a x_1·x_2=\frac{-b+\sqrt{b^2-4ac}}{2a}*\frac{-b-\sqrt{b^2-4ac}}{2a}=\frac{c}{a} x1⋅x2=2a−b+b2−4ac∗2a−b−b2−4ac=ac
⟹ \Longrightarrow ⟹ 弦长公式为 ∣ x 1 − x 2 ∣ = ∣ − b + △ 2 a − − b − △ 2 a ∣ = △ ∣ a ∣ |x_1-x_2|=|\frac{-b+\sqrt{△}}{2a}-\frac{-b-\sqrt{△}}{2a}|=\frac{\sqrt{△}}{|a|} ∣x1−x2∣=∣2a−b+△−2a−b−△∣=∣a∣△
⟹ \Longrightarrow ⟹ 顶点△面积为 1 2 ⋅ ∣ y ∣ ⋅ ∣ x 1 − x 2 ∣ = ∣ -△ 4 a ∣ ∗ △ ∣ a ∣ = ( △ ) 3 8 a 2 \frac{1}{2}·|y|·|x_1-x_2|=|\frac{-△}{4a}|*\frac{\sqrt{△}}{|a|}=\frac{(\sqrt{△})^3}{8a^2} 21⋅∣y∣⋅∣x1−x2∣=∣4a-△∣∗∣a∣△=8a2(△)3
4.韦达定理: x 1 + x 2 = − b a x_1+x_2=-\frac{b}{a} x1+x2=−ab, x 1 ⋅ x 2 = c a x_1·x_2=\frac{c}{a} x1⋅x2=ac, ∣ x 1 − x 2 ∣ = b 2 − 4 a c ∣ a ∣ |x_1-x_2|=\frac{\sqrt{b^2-4ac}}{|a|} ∣x1−x2∣=∣a∣b2−4ac
⟹ \Longrightarrow ⟹ 求出关于两个根的对称轮换式的数值
⟹ \Longrightarrow ⟹ 判断两根符号情况
⟹ \Longrightarrow ⟹ 一元三次方程 a x 3 + b x 2 + c x + d = 0 ax^3+bx^2+cx+d=0 ax3+bx2+cx+d=0的韦达定理: x 1 + x 2 + x 3 = − b a x_1+x_2+x_3=-\frac{b}{a} x1+x2+x3=−ab, x 1 x 2 x 3 = − d a x_1x_2x_3=-\frac{d}{a} x1x2x3=−ad, x 1 x 3 + x 2 x 3 + x 1 x 3 = c a x_1x_3+x_2x_3+x_1x_3=\frac{c}{a} x1x3+x2x3+x1x3=ac
⟹ \Longrightarrow ⟹
理解记忆法
求根公式推导
https://www.bilibili.com/read/cv4538376/
韦达定理、弦长公式、顶点△面积推导
韦达定理、弦长公式、顶点△面积由求根公式推导而来
x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△
⟹ \Longrightarrow ⟹ 韦达定理为 x 1 + x 2 = − b + △ 2 a + − b − △ 2 a = − b a x_1+x_2=\frac{-b+\sqrt{△}}{2a}+\frac{-b-\sqrt{△}}{2a}=-\frac{b}{a} x1+x2=2a−b+△+2a−b−△=−ab
⟹ \Longrightarrow ⟹ 韦达定理为 x 1 ⋅ x 2 = − b + b 2 − 4 a c 2 a ∗ − b − b 2 − 4 a c 2 a = c a x_1·x_2=\frac{-b+\sqrt{b^2-4ac}}{2a}*\frac{-b-\sqrt{b^2-4ac}}{2a}=\frac{c}{a} x1⋅x2=2a−b+b2−4ac∗2a−b−b2−4ac=ac
⟹ \Longrightarrow ⟹ 弦长公式为 ∣ x 1 − x 2 ∣ = ∣ − b + △ 2 a − − b − △ 2 a ∣ = △ ∣ a ∣ |x_1-x_2|=|\frac{-b+\sqrt{△}}{2a}-\frac{-b-\sqrt{△}}{2a}|=\frac{\sqrt{△}}{|a|} ∣x1−x2∣=∣2a−b+△−2a−b−△∣=∣a∣△
⟹ \Longrightarrow ⟹ 顶点△面积为 1 2 ⋅ ∣ y ∣ ⋅ ∣ x 1 − x 2 ∣ = ∣ -△ 4 a ∣ ∗ △ ∣ a ∣ = ( △ ) 3 8 a 2 \frac{1}{2}·|y|·|x_1-x_2|=|\frac{-△}{4a}|*\frac{\sqrt{△}}{|a|}=\frac{(\sqrt{△})^3}{8a^2} 21⋅∣y∣⋅∣x1−x2∣=∣4a-△∣∗∣a∣△=8a2(△)3
or
由韦达定理的结论和完全平方公式可推出:
∣ x 1 − x 2 ∣ = ( x 1 + x 2 ) 2 − 4 x 1 x 2 = b 2 − 4 a c ∣ a ∣ |x_1-x_2|=\sqrt{(x_1+x_2)^2-4x_1x_2}=\frac{\sqrt{b^2-4ac}}{|a|} ∣x1−x2∣=(x1+x2)2−4x1x2=∣a∣b2−4ac = △ ∣ a ∣ =\frac{\sqrt{△}}{|a|} =∣a∣△
根的区间之理解
结合图像,就很容易理解了,所以“根的区间判定”,结合图像,是最快的。

以下是其他角度总结,但是缺少图像,不怎么好快速理解:
区问根问题,常使用 “ 两点式 ” 解题法,即看顶点(横坐标相当于看对称轴,纵坐标相当于看 △ △ △)、看端点(根所分布区问的端点)。
为了讨论方便,只讨论 a > 0 a>0 a>0的情况,考试时,若a的符号不定,则需要讨论开口方向。



归类记忆法
根的分布问题:正负根问题和区间根问题


记忆宫殿法
谐音记忆法
求根公式 x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△很重要
快速秒杀法
图形结合法
结合图像,就很容易理解了,所以“根的区间判定”,结合图像,是最快的。
那怎么记忆住这种方式呢
“根的区间”判定:画图+三要素, △ △ △、对称轴和端点代入。
or
根的区间:看顶点(横坐标相当于看对称轴,纵坐标相当于看 △ △ △)、看端点(根所分布区问的端点)。即:遇到根的区间,就联想到横纵坐标,即需要确定横坐标的位置,纵坐标是否存在,但是有这两个还不够,需要第三者加入,即端点代入后的正负,可以决定整个图像的位置。

转图像记忆法
结合字母编码
学习记忆——英语——字母编码
-
求根公式
x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△,很重要,可以推导出韦达定理等,故事如下:两个苹果(a)上面有个士兵(±),左手拿着香蕉(b)挡住箭(-),右边是一座桥,桥底有一个三角形。

-
一元二次方程的根: x = − b 2 a x=-\frac{b}{2a} x=−2ab:2座桥,桥上有一个香蕉,桥底有两个苹果。
或者:两颗苹果上面有根香蕉,要想托稳香蕉,得有两个横版(一个负号,一个除号)。

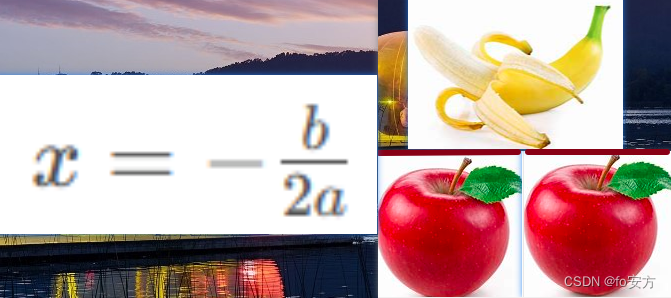
或者两个苹果上面有一座桥和一根香蕉

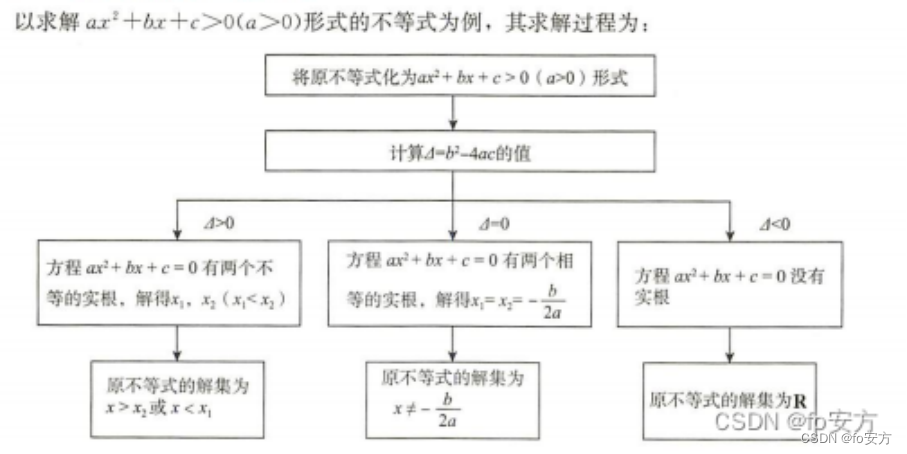
3. y = a x 2 + b x + c y=ax^2+bx+c y=ax2+bx+c的最值: 4 a c − b 2 4 a \frac{4ac-b^2}{4a} 4a4ac−b2 =— △ 4 a \frac{△}{4a} 4a△
4颗苹果上面有两座桥,桥上有一个三角形。


- 韦达定理
x为剪刀,a苹果,b香蕉,c月亮
剪头➕剪刀可以换,苹果顶着负香蕉
剪刀,剪刀,剪刀,可以换,苹果顶着月亮

相关文章:

学习记忆——数学篇——案例——代数——方程——一元二次方程
重点记忆法 a x 2 b x c 0 ax^2bxc0 ax2bxc0 整体可以由: 根(多少,正负,区间) ⟹ \Longrightarrow ⟹ △ △ △ ⟹ \Longrightarrow ⟹ 求根公式 x 1 , 2 x_{1,2} x1,2 − b △ 2 a \frac{-b\sqrt{△}}{2a} 2…...

接口测试及常用接口测试工具
首先,什么是接口呢? 接口一般来说有两种,一种是程序内部的接口,一种是系统对外的接口。 系统对外的接口:比如你要从别的网站或服务器上获取资源或信息,别人肯定不会把数据库共享给你,他只能给你…...
)
【java学习】数组中涉及的常见算法-含冒泡排序(11)
文章目录 1. 最大值、最小值、总和、平均数2. 数组的复制、反转3. 数组元素的排序3.1. 排序方式3.1.1. 冒泡排序 1. 最大值、最小值、总和、平均数 代码如下: public class Test1 {public static void main (String[] args) {int[] arr new int[] {4,2,7,1,3,5};/…...

useEffect Hook使用纠错
React的useEffect Hook是用于处理副作用操作的重要工具。副作用操作通常包括数据获取、订阅、手动DOM操作等。在使用useEffect时,有一些常见的错误和最佳实践需要注意。 以下是一些常见的useEffect使用错误以及如何解决它们的建议: 未清除订阅或定时器…...

LeetCode【739】每日温度
题目: 思路: https://www.bilibili.com/video/BV1PJ411H7P7/?spm_id_from333.337.search-card.all.click&vd_source2f682a60feabf0f730ad09e0f980ce83 单调栈 思考: 解决栈类问题,思考入栈,出栈条件;…...
核桃派walnutpi添加红外遥控器键盘映射(其他的linux板子同理)ir-keytable
01studio终于又发布新品了,全志h616 linux开发板核桃派,正好我也打算学习linux,做为我的启蒙公司,必须支持果断入了一个。 这个板子自带红外接收头,比较少见,一般都需要自己加,看官网文档&…...
-launch-lua的配置)
cartographer(2)-launch-lua的配置
1.了解bag 1roscore2rosbag info rslidar-outdoor-gps.bag了解bag中topic的名称与类型duration: 3:33s types: geometry_msgs?QuaternionStamped nav_msgs_Odometry sensor_msgs/Imu sensor_msgs/IaserScan sensor_msgs/NavSatFix sensor_msgs/PointCloud2 tf2 msgs/TFMe…...
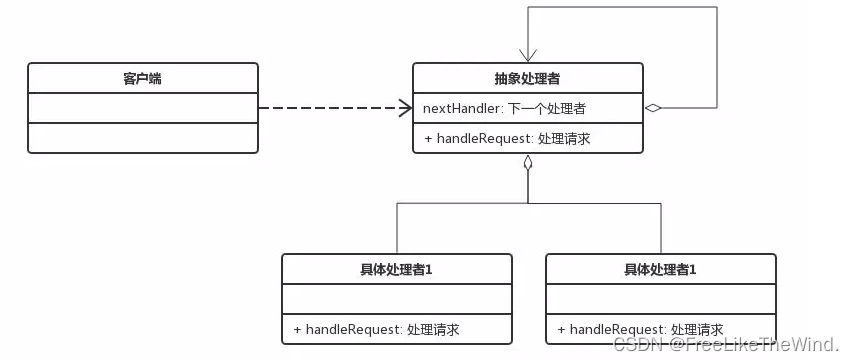
【C++设计模式之责任链模式:行为型】分析及示例
简介 责任链模式是一种行为型设计模式,它允许将请求沿着处理链传递,直到有一个处理器能够处理该请求。这种模式将请求的发送者和接收者解耦,同时提供了更高的灵活性和可扩展性。 描述 责任链模式由多个处理器组成一个处理链,每…...

如何选择编程语言Python Go还是Rust?
选择编程语言需要考虑多个方面,包括语言的特性、社区支持、工作机会、学习曲线等。下面是关于Python Go和Rust的一些介绍。 1.基本语法 1. Python: Python 是一种脚本语言,以简洁、易读的语法著称。以下是 Python 的基本语法示例: # Hello…...
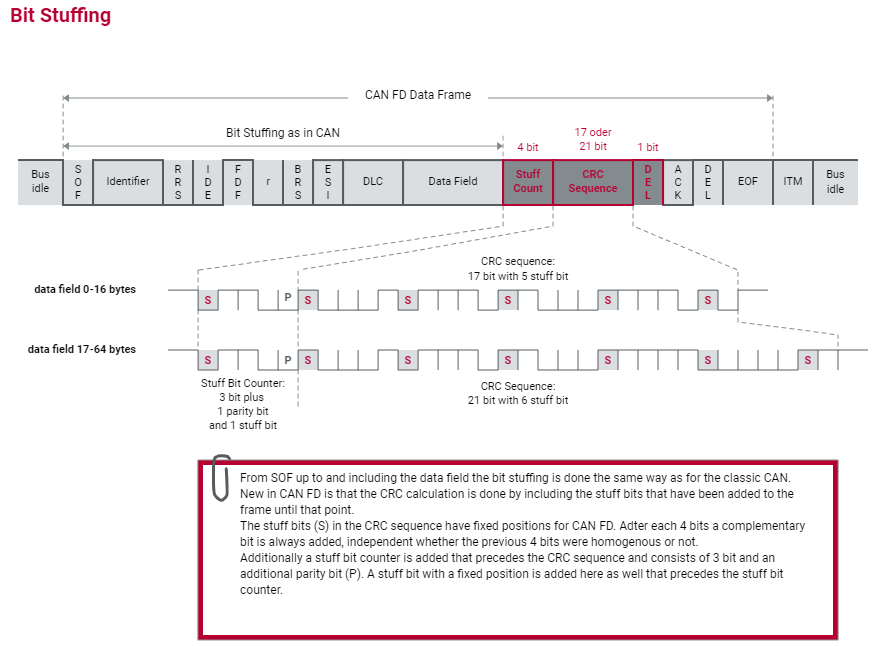
CAN和CANFD通信介绍
CAN(Controller Area Network,控制器局域网)是一种串行通信技术,专门用于在汽车电子控制单元(ECU)之间实现可靠的数据交换。 CAN协议介绍 电子化 汽车近年来的发展呈现出以电子化为主的特点。电子化的主…...

解决网页 H5 对接微信 JSSDK 后自定义分享和跳转APP等没效果
导致的原因 在聊天窗口直接点击一个文本链接,现在微信JSSDK已经不支持这样使用。 解决办法1 将文本链接生成一个二维码,然后微信扫码进入这个链接。 解决办法2 将这个文本链接收藏,然后从收藏打开这个链接。...

基于DeOldify的给黑白照片、视频上色
老照片常常因为当时的技术限制而只有黑白版本。然而现代的 AI 技术,如 DeOldify,可以让这些照片重现色彩。 本教程将详细介绍如何使用 DeOldify 来给老照片上色。 文章目录 准备工作执行代码图片上色视频上色 总结 准备工作 这里用 git clone 命令克隆…...

腾讯云饥荒服务器配置选择和费用价格表
腾讯云饥荒服务器配置选择和费用价格表,腾讯云饥荒服务器配置怎么选择?CPU内存几核几G合适?饥荒服务器配置:建议2核4G起步,可以加载更多的MOD,不会太卡。因为15MOD启动后会占用1GB多内存,这是32…...
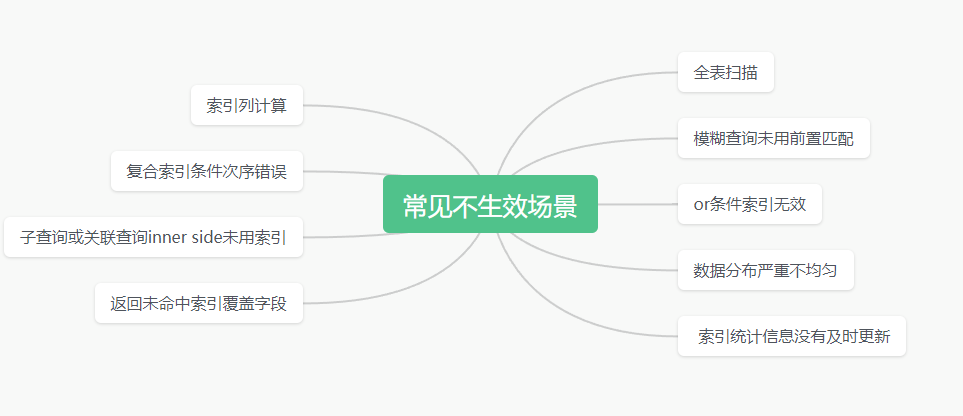
聊聊MySql索引的类型以及失效场景
文章目录 概念常见的索引1.B树索引2.哈希索引3.全文索引4.空间索引5.聚集索引 如何设计合理?1.明确索引需求2.选择索引列3.选择索引类型4.考虑索引维护开销5.设计联合索引6.删除不必要索引7.关注索引统计信息8.测试查询效果 常见不生效场景1.全表扫描2.索引列计算3.…...
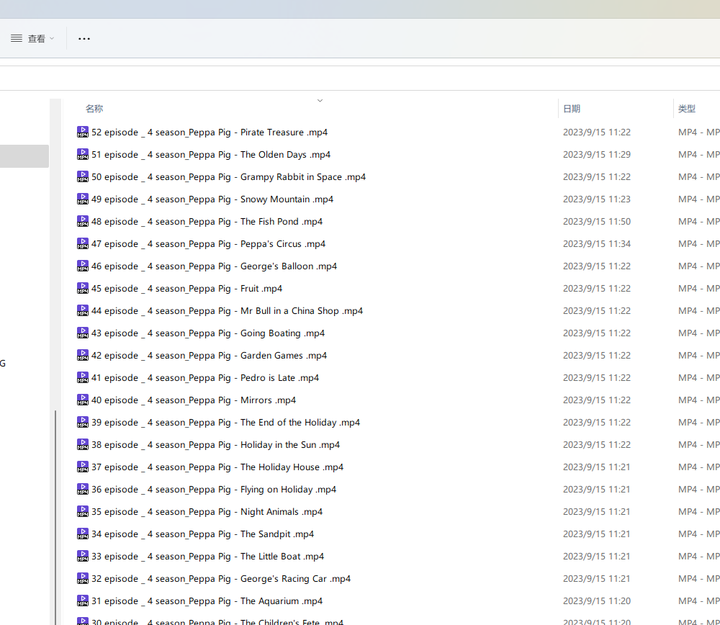
零代码编程:用ChatGPT批量调整文件名称中的词汇顺序
文件夹里面很多文件,需要批量挑战标题中的一些词组顺序:“Peppa Pig - Kylie Kangaroo (14 episode _ 4 season) [HD].mp4”这个文件名改成“14 episode _ 4 season _ Peppa Pig - Kylie Kangaroo.mp4”,可以在ChatGPT中输入提示词࿱…...
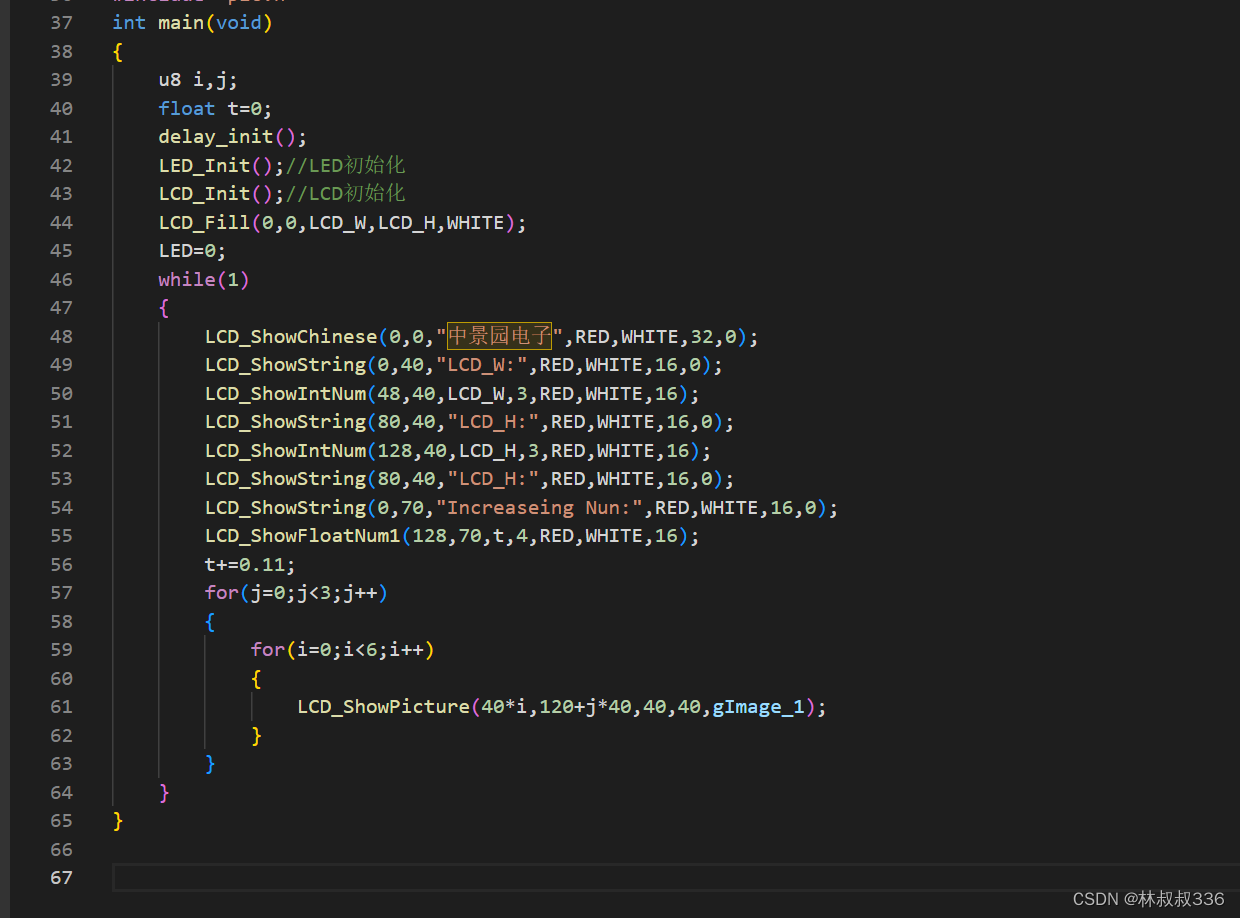
stm32 hal库 st7789 1.54寸lcd
文章目录 前言一、软件spi1.cubemx配置2.源码文件 二、硬件spi1.cubemx配置2.源码文件3.小小修改 总结 前言 1.54寸lcd 240*240 一、软件spi 1.cubemx配置 一定要注意把这几个东西上拉。 使用c8 2.源码文件 我使用的是中景园的源码,他本来是是标准库的稍微修改…...

【arm实验1】GPIO实验-LED灯的流水亮灭
linuxlinux:~/study/01-asm$ cat asm-led.S .text .global _start _start: 1.设置GPIOE寄存器的时钟使能 RCC_MP_AHB4ENSETR[4]->1 0x50000a28 LDR R0,0X50000A28 LDR R1,[R0] 从r0为起始地址的4字节数据取出放在R1 ORR R1,R1,#(0x1<<4) 第4位设置为1 ORR R…...

MySQL关联数据表操作方式
1、准备工作(创建数据表) create table employee( emp_id int primary key, name varchar(20), birth_date date, sex varchar(1), salary int, branch_id int, sup_id int );create table client( client_id int primary key, client_name varchar(20)…...
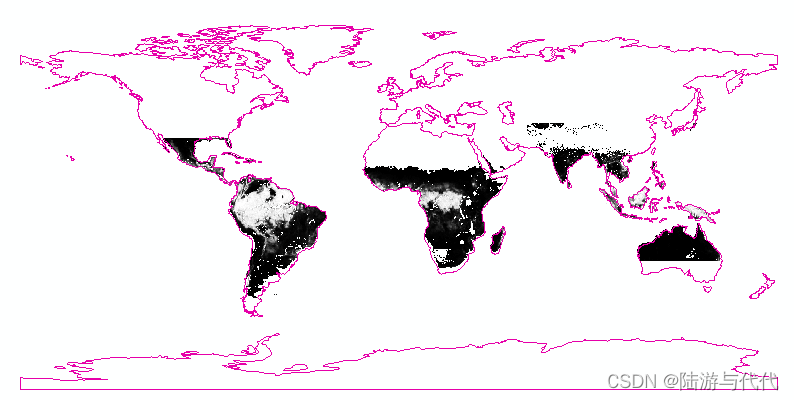
SMOS数据处理,投影变换,‘EPSG:6933‘转为‘EPSG:4326‘
在处理SMOS数据时,遇到了读取nc数据并存为tif后,影像投影无法改变,因此全球数据无法重叠。源数据的投影为EPSG:6933,希望转为EPSG:4326。 解决代码。 python import os import netCDF4 as nc import numpy as np from osgeo impo…...
游戏服务端性能测试实战总结
导语:近期经历了一系列的性能测试,涵盖了Web服务器和游戏服务器的领域。在这篇文章中,我将会对游戏服务端所做的测试进行详细整理和记录。需要注意的是,本文着重于记录,而并非深入的编程讨论。在这里,我将与…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
