2023NOIP A层联测6 数点
题目大意
给你一个排列 p p p,对于每一个 i i i,我们在平面上,放置一个点 ( i , p i ) (i,p_i) (i,pi)。对于坐标上下限都在 1 ∼ n 1\sim n 1∼n内的全体 ( n ( n + 1 ) 2 ) 2 (\frac{n(n+1)}{2})^2 (2n(n+1))2矩形,求每个矩形内部点数的 k k k次方之和。
形式化地,请你计算
∑ 1 ≤ l ≤ r ≤ n ∑ 1 ≤ d ≤ u ≤ n ∣ { i ∣ l ≤ i ≤ r ∨ d ≤ p i ≤ u } ∣ \sum\limits_{1\leq l\leq r\leq n}\sum\limits_{1\leq d\leq u\leq n}|\{i|l\leq i\leq r\vee d\leq p_i\leq u\}| 1≤l≤r≤n∑1≤d≤u≤n∑∣{i∣l≤i≤r∨d≤pi≤u}∣
1 ≤ n ≤ 1 0 5 , 1 ≤ k ≤ 3 1\leq n\leq 10^5,1\leq k\leq 3 1≤n≤105,1≤k≤3
题解
我们可以考虑拆贡献,点数的 k k k次方可以看成选 k k k个点的方案的线性组合。
什么意思呢?就是在这 n n n个点中有序地可重地选择 k k k个点,将所有包含这 k k k个点的矩形的贡献 + 1 +1 +1,注意所有从 n n n个点中有序地可重地选 k k k个点的方案都要被计算贡献。
为什么可以这样呢?对于每个矩形,设这个矩形内的点数为 t t t,在这个矩形中有序地可重地选 k k k个点的方案数为 t k t^k tk,也就是说这个矩形在上面计算贡献的时候将贡献加了 t k t^k tk次一。
下面,我们来求 k k k为不同的值时的答案。
当 k = 1 k=1 k=1时
对每个点 ( x , p x ) (x,p_x) (x,px),答案的贡献增加 x × ( n − x + 1 ) × p x × ( n − p x + 1 ) x\times (n-x+1)\times p_x\times (n-p_x+1) x×(n−x+1)×px×(n−px+1)。
当 k = 2 k=2 k=2时
我们考虑选的两个点相同的情况和两个点不同的情况。
对于两个点相同的情况,这其实就是 k = 1 k=1 k=1的情况,每种情况会被算一次。
对于两个点不同的情况,我们可以分为顺序对和逆序对来考虑:
- 对于顺序对 x < y , p x < p y x<y,p_x<p_y x<y,px<py,其贡献为 x × p x × ( n − y + 1 ) × ( n − p y + 1 ) x\times p_x\times (n-y+1)\times (n-p_y+1) x×px×(n−y+1)×(n−py+1),将 x × p x x\times p_x x×px存入树状数组中,再用 ( n − y + 1 ) × ( n − p y + 1 ) (n-y+1)\times (n-p_y+1) (n−y+1)×(n−py+1)来乘即可
- 对于逆序对 x < y , p x > p y x<y,p_x>p_y x<y,px>py将排列翻转之后按顺序对的方法来做即可
因为选点是有序的,每种顺序对和逆序对都用两种选法被选到,所以两个点不同的情况的贡献要乘 2 2 2。
当 k = 3 k=3 k=3时
将 k = 1 k=1 k=1的贡献计算一次(三次选择同一个点), k = 2 k=2 k=2的贡献计算两次(三次选择两个不同的点),下面再考虑三次选择三个不同的点的贡献。
分为两种本质不同的情况:
情况1
------
|* |
| * |
| * |
------
这种情况出现了 2 2 2次(按 i i i左右翻转,总共有 2 2 2次),用两个树状数组维护即可。
情况2
------
| * |
|* |
| * |
------
这种情况总共出现了 4 4 4次(按 i i i左右翻转,按 p i p_i pi上下翻转,四个角度各一次,总共有 4 4 4次),用线段树来维护即可。可以在加入第一个点时直接在对应位置上加数,在加入第二个点时将其后缀乘上对应的数,再加入第三个点时查询前缀和。
因为选点是有序的,每种顺序对和逆序对都用六种选法被选到,所以两个点不同的情况的贡献要乘 6 6 6。
时间复杂度为 O ( n log n ) O(n\log n) O(nlogn)。
code
#include<bits/stdc++.h>
#define lc k<<1
#define rc k<<1|1
using namespace std;
const long long mod=998244353;
int n,K,p[100005];
long long tr1[100005],tr2[100005];
long long s[500005],hv[500005],ly[500005];
int lb(int i){return i&(-i);
}
void pt1(int i,long long v){while(i<=n){tr1[i]=(tr1[i]+v)%mod;i+=lb(i);}
}
long long find1(int i){long long re=0;while(i){re=(re+tr1[i])%mod;i-=lb(i);}return re;
}
void pt2(int i,long long v){while(i<=n){tr2[i]=(tr2[i]+v)%mod;i+=lb(i);}
}
long long find2(int i){long long re=0;while(i){re=(re+tr2[i])%mod;i-=lb(i);}return re;
}
void build(int k,int l,int r){s[k]=hv[k]=ly[k]=0;if(l==r) return;int mid=l+r>>1;build(lc,l,mid);build(rc,mid+1,r);
}
void down(int k){s[lc]=(s[lc]+hv[lc]*ly[k])%mod;s[rc]=(s[rc]+hv[rc]*ly[k])%mod;ly[lc]=(ly[lc]+ly[k])%mod;ly[rc]=(ly[rc]+ly[k])%mod;ly[k]=0;
}
void ch(int k,int l,int r,int x,long long y){if(l==r&&l==x){hv[k]=y;s[k]=ly[k]=0;return;}if(ly[k]) down(k);int mid=l+r>>1;if(x<=mid) ch(lc,l,mid,x,y);else ch(rc,mid+1,r,x,y);hv[k]=(hv[lc]+hv[rc])%mod;s[k]=(s[lc]+s[rc])%mod;
}
void ts(int k,int l,int r,int x,int y,long long v){if(l>=x&&r<=y){ly[k]=(ly[k]+v)%mod;s[k]=(s[k]+v*hv[k])%mod;return;}if(ly[k]) down(k);int mid=l+r>>1;if(x<=mid) ts(lc,l,mid,x,y,v);if(y>mid) ts(rc,mid+1,r,x,y,v);s[k]=(s[lc]+s[rc])%mod;
}
long long find(int k,int l,int r,int x,int y){if(l>=x&&r<=y) return s[k];if(ly[k]) down(k);int mid=l+r>>1;long long re=0;if(x<=mid) re=(re+find(lc,l,mid,x,y))%mod;if(y>mid) re=(re+find(rc,mid+1,r,x,y))%mod;return re;
}
long long gt(){long long re=0;build(1,1,n);for(int i=1;i<=n;i++){re=(re+find(1,1,n,1,p[i])*(n-i+1)%mod*(n-p[i]+1)%mod)%mod;ts(1,1,n,p[i],n,p[i]);ch(1,1,n,p[i],i);}return re;
}
long long gt1(){long long re=0;for(int i=1;i<=n;i++){re=(re+1ll*i*(n-i+1)%mod*p[i]%mod*(n-p[i]+1)%mod)%mod;}return re;
}
long long gt2(){long long re=0;for(int i=1;i<=n;i++){re=(re+find1(p[i])*(n-i+1)%mod*(n-p[i]+1)%mod)%mod;pt1(p[i],1ll*i*p[i]%mod);}for(int i=1;i<=n;i++){tr1[i]=0;if(i<n-i+1) swap(p[i],p[n-i+1]);}for(int i=1;i<=n;i++){re=(re+find1(p[i])*(n-i+1)%mod*(n-p[i]+1)%mod)%mod;pt1(p[i],1ll*i*p[i]%mod);}for(int i=1;i<=n;i++){tr1[i]=0;if(i<n-i+1) swap(p[i],p[n-i+1]);}return re;
}
long long gt3(){long long re=0;for(int i=1;i<=n;i++){long long now=find1(p[i]);pt1(p[i],1ll*i*p[i]%mod);re=(re+find2(p[i])*(n-i+1)%mod*(n-p[i]+1)%mod)%mod;pt2(p[i],now);}for(int i=1;i<=n;i++){tr1[i]=tr2[i]=0;if(i<n-i+1) swap(p[i],p[n-i+1]);}for(int i=1;i<=n;i++){long long now=find1(p[i]);pt1(p[i],1ll*i*p[i]%mod);re=(re+find2(p[i])*(n-i+1)%mod*(n-p[i]+1)%mod)%mod;pt2(p[i],now);}for(int i=1;i<=n;i++){tr1[i]=tr2[i]=0;if(i<n-i+1) swap(p[i],p[n-i+1]);}re=(re+gt())%mod;for(int i=1;i<=n;i++)if(i<n-i+1) swap(p[i],p[n-i+1]);re=(re+gt())%mod;for(int i=1;i<=n;i++)p[i]=n-p[i]+1;re=(re+gt())%mod;for(int i=1;i<=n;i++)if(i<n-i+1) swap(p[i],p[n-i+1]);re=(re+gt())%mod;return re;
}
int main()
{freopen("points.in","r",stdin);freopen("points.out","w",stdout);scanf("%d%d",&n,&K);for(int i=1;i<=n;i++){scanf("%d",&p[i]);}if(K==1) printf("%lld",gt1());else if(K==2) printf("%lld",(gt1()+2*gt2())%mod);else{printf("%lld",(gt1()+6*gt2()+6*gt3())%mod);}return 0;
}
相关文章:

2023NOIP A层联测6 数点
题目大意 给你一个排列 p p p,对于每一个 i i i,我们在平面上,放置一个点 ( i , p i ) (i,p_i) (i,pi)。对于坐标上下限都在 1 ∼ n 1\sim n 1∼n内的全体 ( n ( n 1 ) 2 ) 2 (\frac{n(n1)}{2})^2 (2n(n1))2矩形,求每个矩形…...
Jmeter 链接MySQL测试
1.环境部署 1.1官网下载MySQL Connector https://dev.mysql.com/downloads/connector/j/ 1.2 解压后,将jar放到jmeter/lib目录下 1.3 在测试计划中添加引用 2.脚本设置 2.1设置JDBC Connection Configuration 先添加一个setUp线程中,在setUp中添加“…...

jwt的了解和使用以及大致代码分析
jwt简介 以下介绍来自官网(https://jwt.io/) SON Web 令牌 (JWT) 是一种开放标准 (RFC 7519),它定义了一种紧凑且独立的方式,用于在各方之间以 JSON 对象的形式安全地传输信息。此信…...

uniapp中videojs、renderjs的使用
在uniapp中使用了某些前端库或iframe,需要操作这些库中的dom的时候, 而uni上又没有document等基础对象。也就无法操作这些dom去实现一些交互逻辑,那么,涉及到这些的前端类库就无法使用,例如html2、canvas、image、vide…...
AIGC AI绘画 Midjourney 参数大全详细列表
AIGC ChatGPT 职场案例 AI 绘画 与 短视频制作, Power BI 商业智能 68集, 数据库Mysql8.0 54集 数据库Oracle21C 142集, Office 2021实战, Python 数据分析, ETL Informatica 案例实战 Excel 2021实操,函数大全,图表大全,大屏可视化制作 加技巧500集 数据分析可视化T…...

安装hadoop,并配置hue
0、说明 对于大数据学习的初始阶段,我也曾尝试搭建相应的集群环境。通过搭建环境了解组件的一些功能、配置、原理。 在实际学习过程中,我更多的还是使用docker来快速搭建环境。 这里记录一下我搭建hadoop的过程。 1、下载hadoop 下载地址:…...
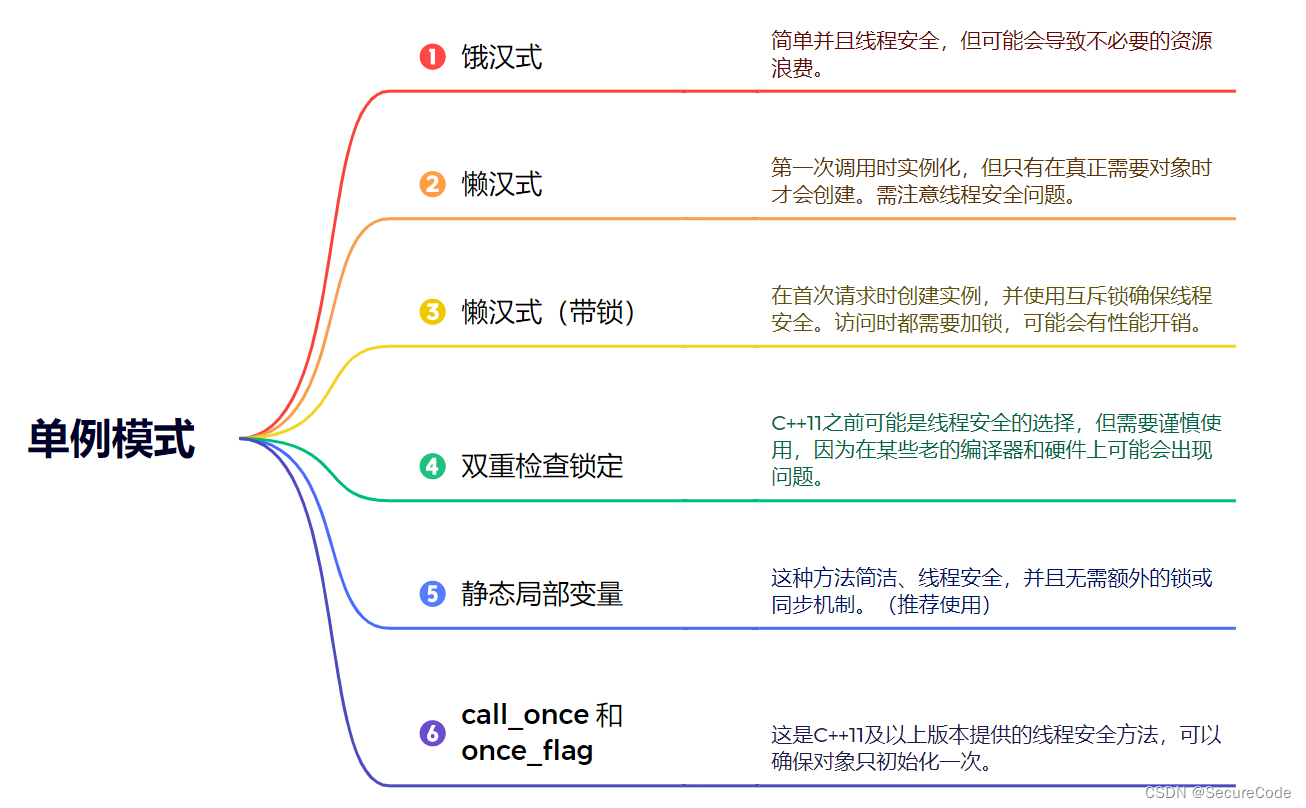
23种经典设计模式:单例模式篇(C++)
前言: 博主将从此篇单例模式开始逐一分享23种经典设计模式,并结合C为大家展示实际应用。内容将持续更新,希望大家持续关注与支持。 什么是单例模式? 单例模式是设计模式的一种(属于创建型模式 (Creational Pa…...

ros中对move_base的调用
move_base包中自带costmap2d, global planner 等功能 也可以直接调用其中make_plan进行路径规划 #include "geometry_msgs/PoseStamped.h" #includde "nav_msgs/GetPlan.h"void fillPathRequest(nav_msgs::GetPlan::Request &request, float start_x…...

Git从本地库撤销已经添加的文件或目录
场景 在提交时, 误将一个目录添加到了暂存区, 而且commit 了本地库,同批次commit 的还有其他需要提交的文件。 commit 之后发现这个目录下所有的文件都不需要提交, 现在需要撤销这个提交, 使这个目录不被push到远端库。 这里以远端服务器github 为例,在Git GUI下看到的…...

百度SEO优化的特点(方式及排名诀窍详解)
百度SEO优化的特点介绍: 百度SEO优化是指对网站进行优化,使其在百度搜索引擎中获得更好的排名,进而获取更多的流量和用户。百度SEO优化的特点是综合性强、效果持久、成本低廉、投资回报高。百度的搜索算法不断更新,所以长期稳定的…...
Gin 文件上传操作(单/多文件操作)
参考地址: 单文件 | Gin Web Framework (gin-gonic.com)https://gin-gonic.com/zh-cn/docs/examples/upload-file/single-file/ 单文件 官方案例: func main() {router := gin.Default()// 为 multipart forms 设置较低的内存限制 (默认是 32 MiB)router.MaxMultipartMem…...

分类预测 | MATLAB实现KOA-CNN-LSTM开普勒算法优化卷积长短期记忆神经网络数据分类预测
分类预测 | MATLAB实现KOA-CNN-LSTM开普勒算法优化卷积长短期记忆神经网络数据分类预测 目录 分类预测 | MATLAB实现KOA-CNN-LSTM开普勒算法优化卷积长短期记忆神经网络数据分类预测分类效果基本描述程序设计参考资料 分类效果 基本描述 1.MATLAB实现KOA-CNN-LSTM开普勒算法优化…...

Qt应用开发(基础篇)——列表视图 QListView
一、前言 QListView类继承于QAbstractItemView类,提供了一个列表或者图标视图的模型。 视图基类 QAbstractItemView QListView效果相当于Windows文件夹右键->查看->图标和列表,使用setViewMode()设置视图模式,并且提供setIconSize()函数…...

vue-6
一、声明式导航-导航链接 1.需求 实现导航高亮效果 如果使用a标签进行跳转的话,需要给当前跳转的导航加样式,同时要移除上一个a标签的样式,太麻烦!!! 2.解决方案 vue-router 提供了一个全局组件 router…...

温度在线检测技术在电力电缆线路的应用
在电力电缆的日常运行检测中,针对电缆温度的状况,所采用的电力温度在线检测技术也得到了大范围的普及。电网系统中,其单位时间内可输送的电力能源受到其温度的变化影响。因此,采用更有效的方式实时检测电缆系统运行温度࿰…...
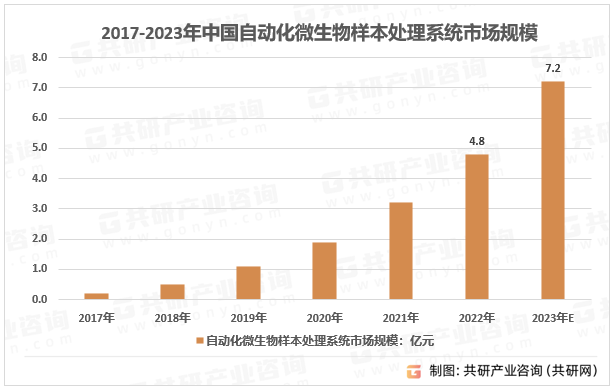
2023年中国自动化微生物样本处理系统竞争现状及行业市场规模分析[图]
微生物检测能够对感染性疾病的病原体或者代谢物进行检测分析,是IVD的细分领域之一。2022年中国体外诊断市场规模1424亿元。 2015-2022年中国体外诊断市场规模 资料来源:共研产业咨询(共研网) 微生物检测由于样本类型多样…...

硬链接和软连接的区别
软链接(也称为软连接或符号链接)是一种特殊的文件,其内容是另一个文件的路径。当你使用软链接时,实际上是在操作另一个文件。软链接的优点是它可以跨文件系统使用,因此可以跨分区或磁盘链接文件。此外,软链…...

保护隐私与增强网络安全之网络代理技术
目录 前言 一、网络代理技术原理 二、网络代理技术类型 1. HTTP代理 2. SOCKS代理 3. DNS代理 4. 加密代理 5. 反向代理 三、网络代理技术应用 1. 加速网络访问速度 2. 绕过网络限制 3. 保护个人隐私 4. 节省带宽 5. 改善网络安全 四、网络代理技术优缺点 网络…...

【每日一题】CF1680C. Binary String | 双指针 | 简单
题目内容 原题链接 给定一个长度为 n n n 的 01 01 01 字符串,对于一个子串 s u b sub sub ,子串内部的 0 0 0 的数量为 x x x ,子串以外的 1 1 1 的数量为 y y y ,子串的代价为 m a x ( x , y ) max(x, y) max(x,y) &…...
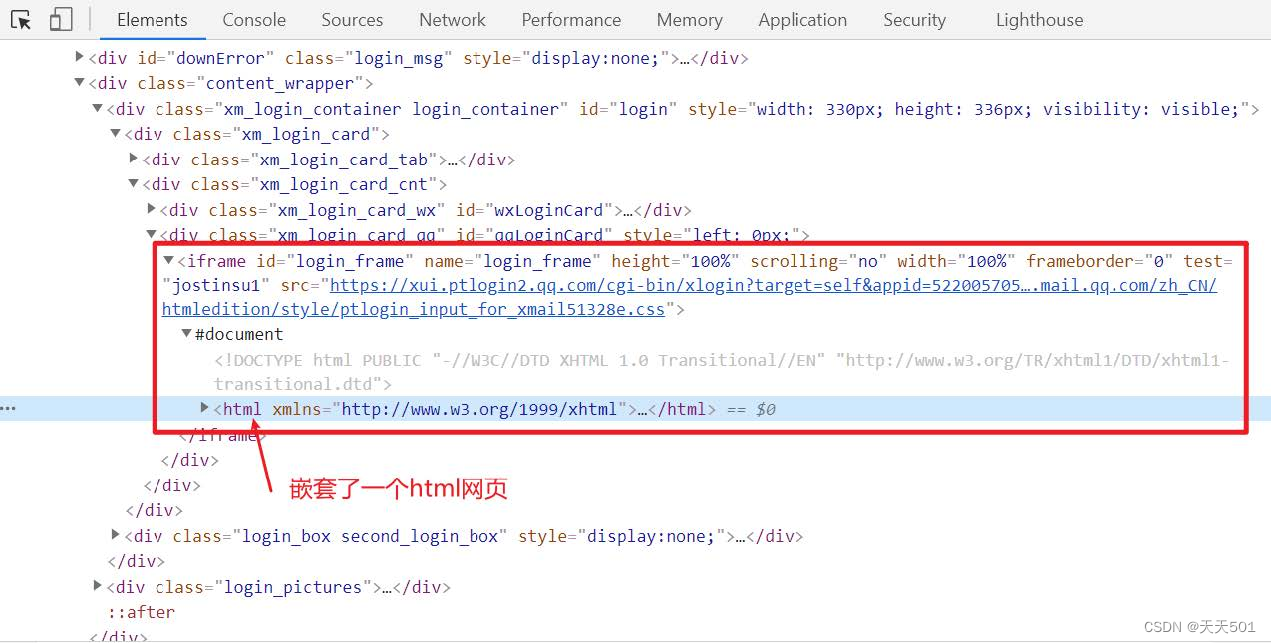
10.selenium进阶
文章目录 1、嵌套网页1、1 什么是嵌套页面1、2 selenium获取嵌套页面的数据 2、执行JavaScript代码3、鼠标动作链4、selenium键盘事件5、其他方法5、1 选择下拉框5、2 弹窗的处理 6、selenium设置无头模式7、selenium应对检测小结 1、嵌套网页 在前端开发中如果有这么一个需…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...
