【数据结构】二叉树的基本概念
1.树概念及结构
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的

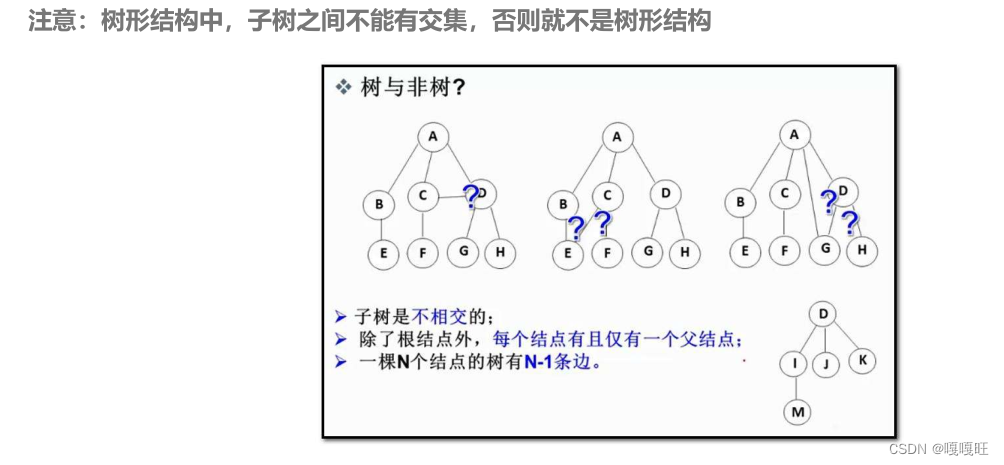
子树不能有交集,就是不能有闭环.N个节点两个一条边,所以是N-1个边,父节点的概念在下面讲.
1.2 树的相关概念

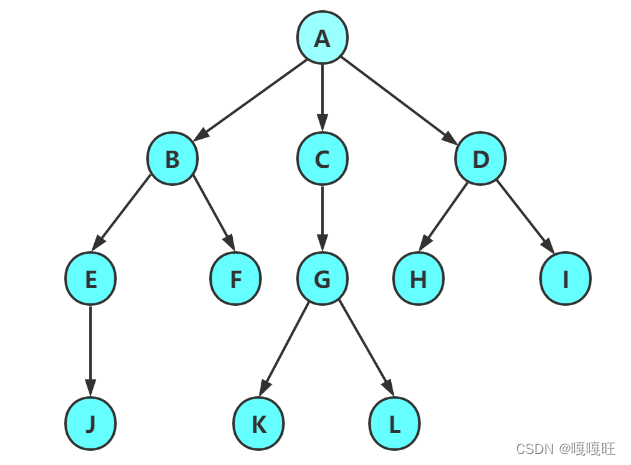
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
1.3 树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
DataType _data; // 结点中的数据域
};
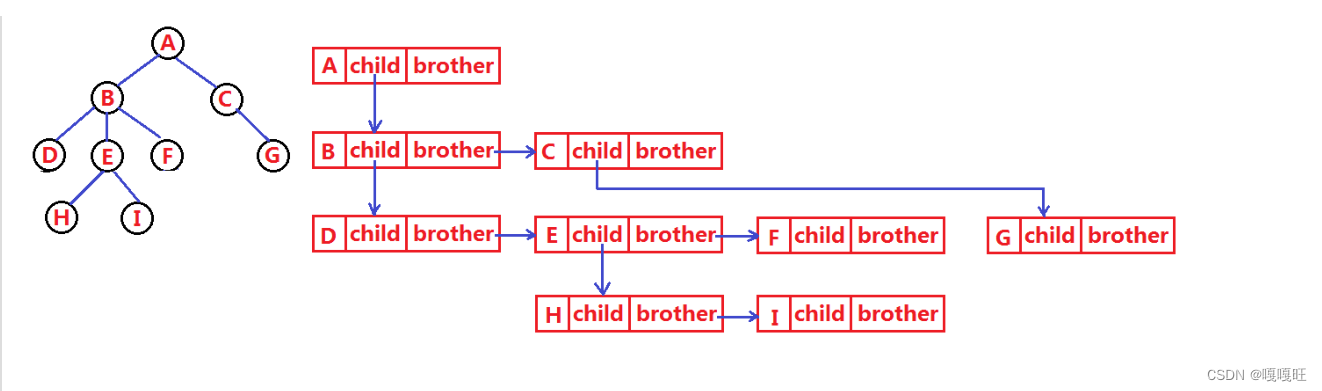
这里父节点只保存第一个孩子的节点,别的孩子由第一个孩子指向,这里c节点也是a的孩子,但是他是由a的第一个孩子b指向的.
2.二叉树概念及结构
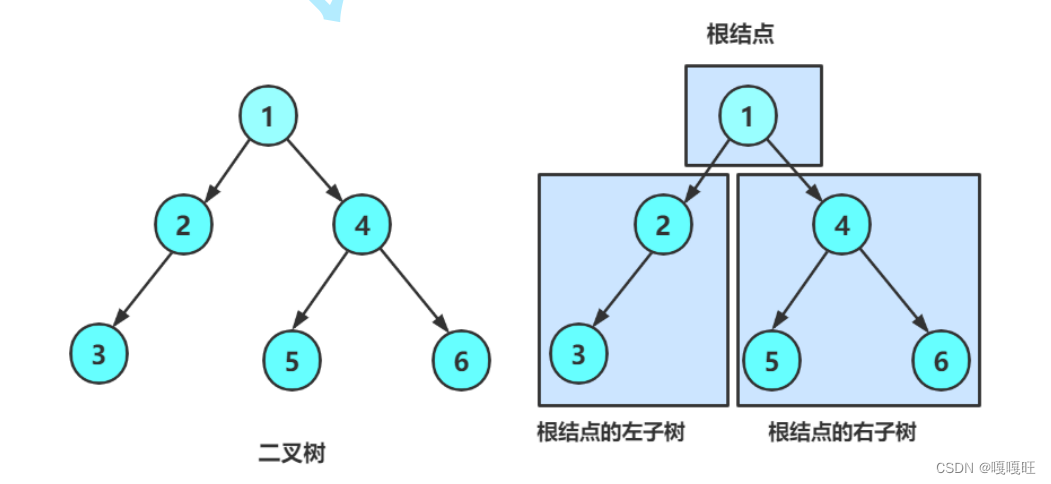
一棵二叉树是结点的一个有限集合,该集合:
-
或者为空
-
由一个根节点加上两棵别称为左子树和右子树的二叉树组成
-
二叉树不存在度大于2的结点//就是不超过两个孩子
-
二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树

这也是个满二叉树,什么是满二叉树呢?
2.3 特殊的二叉树:
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 2的k次方 -1,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
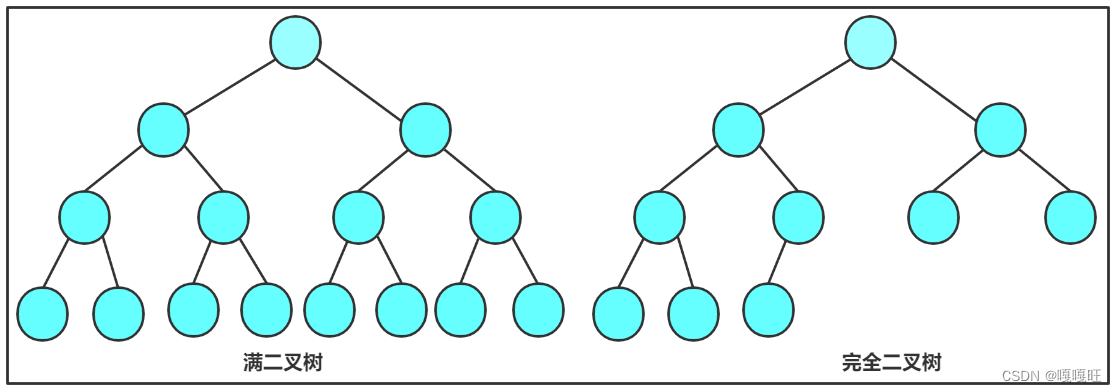

完全二叉树是连续的,不存在上图情况
2.4 二叉树的性质


2.等比数列求和
首项为a1=1,公比为q=2,等比数列求和公式Sn=a1(1-q^n)/(1-q),这里的n取h(深度)
3.

4.根据第二条2^h-1=n
n+1=2^h;
可得第四条
3.二叉树基础计算题
- 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A 不存在这样的二叉树
B 200
C 198
D 199
解析:叶子结点数为度为0的结点数,根据第三条性质,选择b. - 在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
解析:二叉树不存在度大于2的,所以度只有0,1,2,分别记度为0,1,2的结点数目为n0,n1,n2;
n0+n1+n2=2n;n为总结点数,n0=n2+1;度为1的只可能是0,1,因为这个是完全二叉树,有顺序的,不可能出现下图这样
2n0-1+n1=2n;2n0为偶数,2n为偶数,则n1只能取1,则n0=n;选a;
3. 一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
假设树的高度为h,则树的节点范围是最后一行只有一个到最后一行全满,就是2^(h-1)-1+1到全满2的h次方减1;
分别带人选项,选择b.
4. 一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
解析:n0+n1+n2=767;
2n0-1+n1=767
2n0-1为奇数,767为奇数,又因为是完全二叉树,所以n1=0;n0=384,选b;
4. 二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
- 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。

- 链式存储
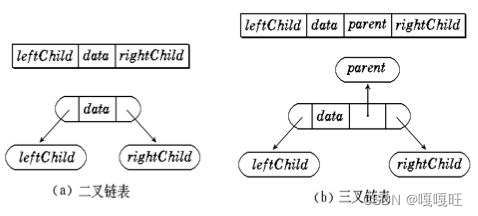
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链.
相关文章:

【数据结构】二叉树的基本概念
1.树概念及结构 1.1树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的 子树不能有交集࿰…...

数据可视化实战:如何给毛*易的歌曲做词云展示?
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据开发、数据分析等。 🐴欢迎小伙伴们点赞👍🏻、收藏⭐️、…...

智能文本纠错API的崭露头角:革命性的写作辅助工具
前言 在数字化时代,文字是我们日常生活和工作中的不可或缺的一部分。不论是在社交媒体上发帖、撰写商务邮件还是完成学术论文,文字表达都是沟通的核心。然而,字词错误、语法错误和敏感信息却是许多人常常面临的挑战,它们不仅会影…...
-3)
读书笔记:多Transformer的双向编码器表示法(Bert)-3
多Transformer的双向编码器表示法 Bidirectional Encoder Representations from Transformers,即Bert; 第3章 Bert实战 学习如何使用预训练的BERT模型: 如何使用预训练的BERT模型作为特征提取器;探究Hugging Face的Transforme…...

jpsall脚本
当一个集群的节点数量增多时,使用jps查看每一个节点的进程这个过程非常繁琐,因此我们可以写一个jpsall脚本,使用循环迭代的方式,在多台远程主机上执行相同的命令,这样就可以节省在每台主机上手动执行命令的时间和精力。…...
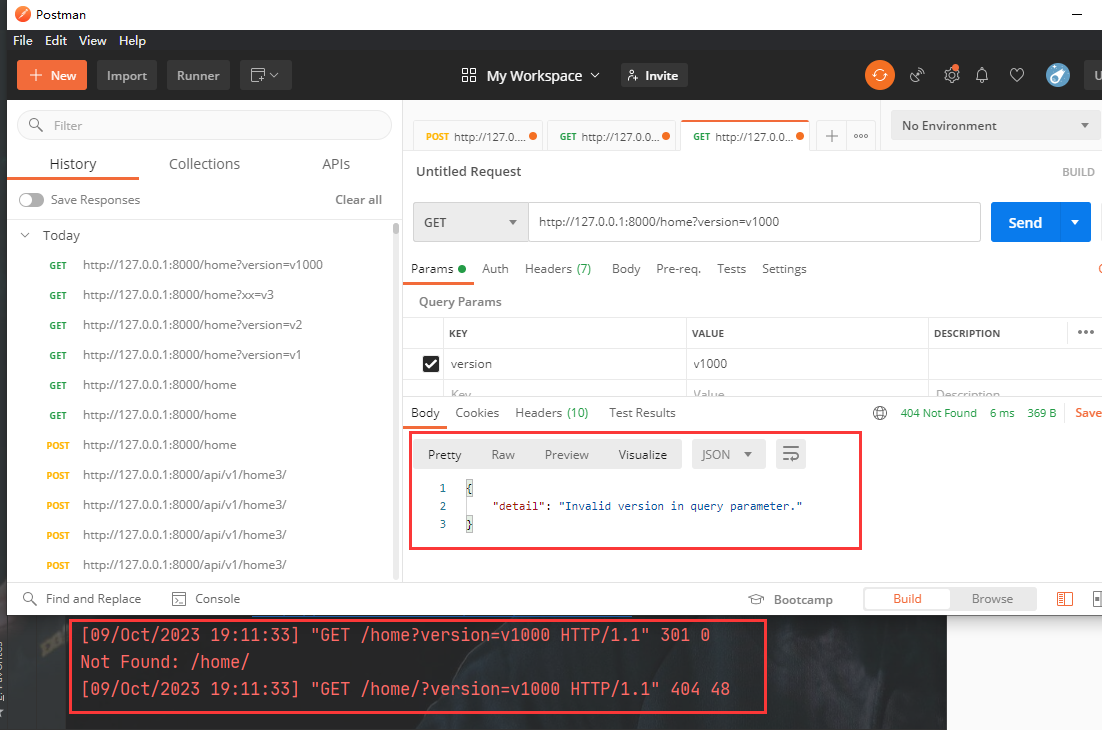
Django REST framework API版本管理【通过GET参数传递】
API版本 在开发过程中可能会有多版本的API,因此需要对API进行管理。django drf中对于版本的管理也很方便。 http://www.example.com/api/v1/info http://www.example.com/api/v2/info 上面这种形式就是很常见的版本管理 在restful规范中,后端的API需…...

归并排序 nO(lgn)
大家好,我是蓝胖子,我一直相信编程是一门实践性的技术,其中算法也不例外,初学者可能往往对它可望而不可及,觉得很难,学了又忘,忘其实是由于没有真正搞懂算法的应用场景,所以我准备出…...
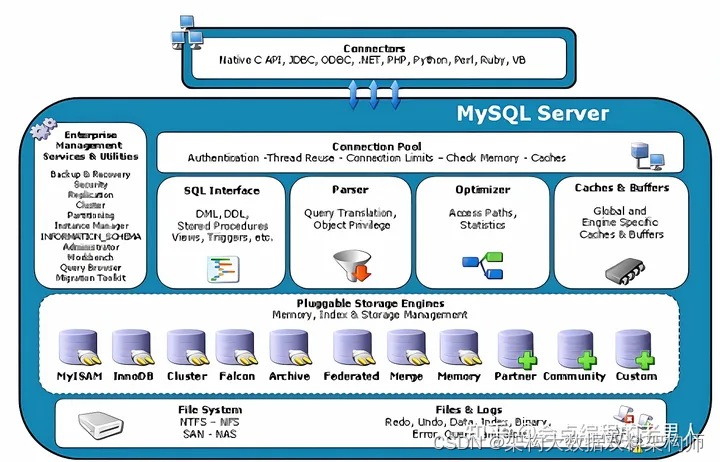
数据库Mysql三大引擎(InnoDB、MyISAM、 Memory)与逻辑架构
MySQL数据库及其分支版本主要的存储引擎有InnoDB、MyISAM、 Memory等。简单地理解,存储引擎就是指表的类型以及表在计算机上的存储方式。存储引擎的概念是MySQL的特色,使用的是一个可插拔存储引擎架构,能够在运行的时候动态加载或者卸载这些存…...
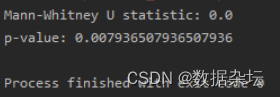
Python数据分析实战-实现Mann-Whitney U检验(附源码和实现效果)
实现功能 使用scipy.stats模块中的mannwhitneyu函数来实现Mann-Whitney U检验,该检验用于比较两个独立样本的分布是否有显著差异。 实现代码 from scipy.stats import mannwhitneyu# 两个独立样本的数据 group1 [1, 2, 3, 4, 5] group2 [6, 7, 8, 9, 10]# 执行…...
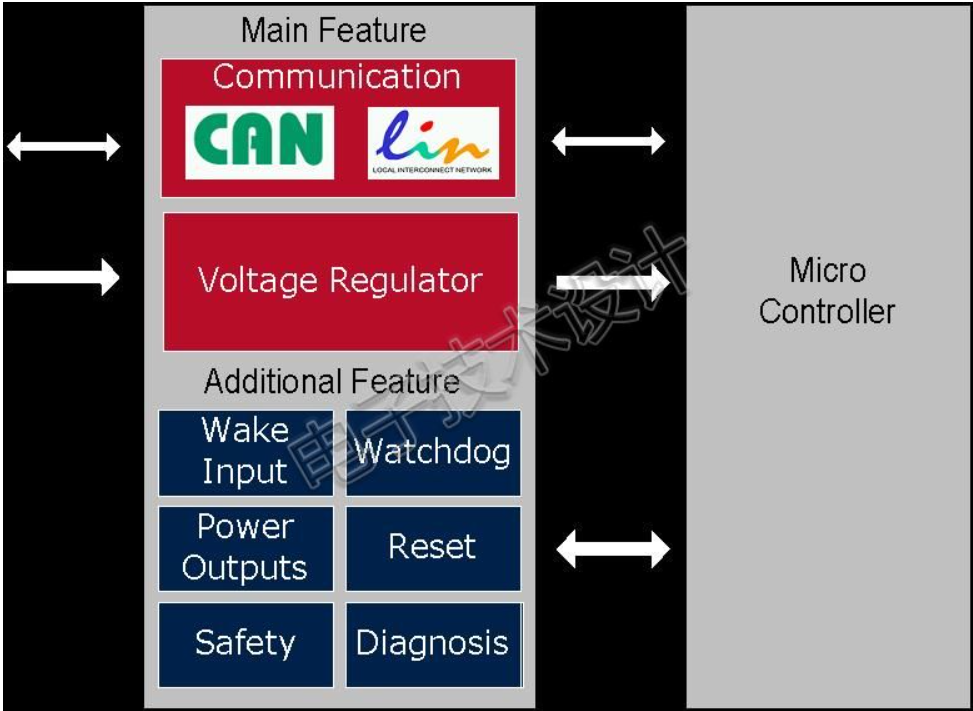
车载SBC芯片概论
+他V hezkz17进数字音频系统研究开发交流答疑群(课题 参考英飞凌SBC官网资料:https://www.infineon.com/cms/cn/product/automotive-system-ic/system-basis-chips-sbc/ SBC芯片在汽车电子领域可谓占一席之地了。那么什么是SBC?怎么用?用在哪里?主要特性? 1.什么是SBC?…...

【ARM AMBA5 CHI 入门 12.1 -- CHI 链路层详细介绍 】
文章目录 CHI 版本介绍1.1 CHI 链路层介绍1.1.1 Flit 切片介绍1.1.2 link layer credit(L-Credit)机制1.1.3 Channel1.1.4 Port1.1. RN Node 接口定义1.1.6 SN Node 接口定义1.2 Channel interface signals1.2.1 Request, REQ, channel1.2.2 Response, RSP, channel1.2.3 Snoop…...

【物联网】Arduino+ESP8266物联网开发(二):控制发光二极管 按钮开关控制开关灯
【物联网】ArduinoESP8266物联网开发(一):开发环境搭建 安装Arduino和驱动 2.ESP8266基础应用 【物联网】ESP8266 开关控制 发光二极管 LED 开发软件下载地址 链接: https://pan.baidu.com/s/1BaOY7kWTvh4Obobj64OHyA?pwd3qv8 提取码: 3qv8 学习过程中会用到的基础…...
WPF向Avalonia迁移(二、一些可能使用到的库)
可能使用到的一些库 1. UI库 开源项目:https://github.com/irihitech/Semi.Avalonia 如果想引用他的DataGrid样式还需要添加Semi.Avalonia.DataGrid 2. 图表库 LiveChartsCore.SkiaSharpView.Avalonia 3.SVG库 开源项目:https://github.com/wieslaw…...
Mac navicat连接mysql出现1045 - Access denied for user ‘root‘
Mac navicat连接mysql出现1045 - Access denied for user ‘root’ 前提:如果你的mac每次开navicat都连接不上,推荐试试我这个方法 1.打开设置–>找到左下角最下面的MySQL–>点击Stop MySQL Server 2.开启一个终端,依次输入以下命令&a…...
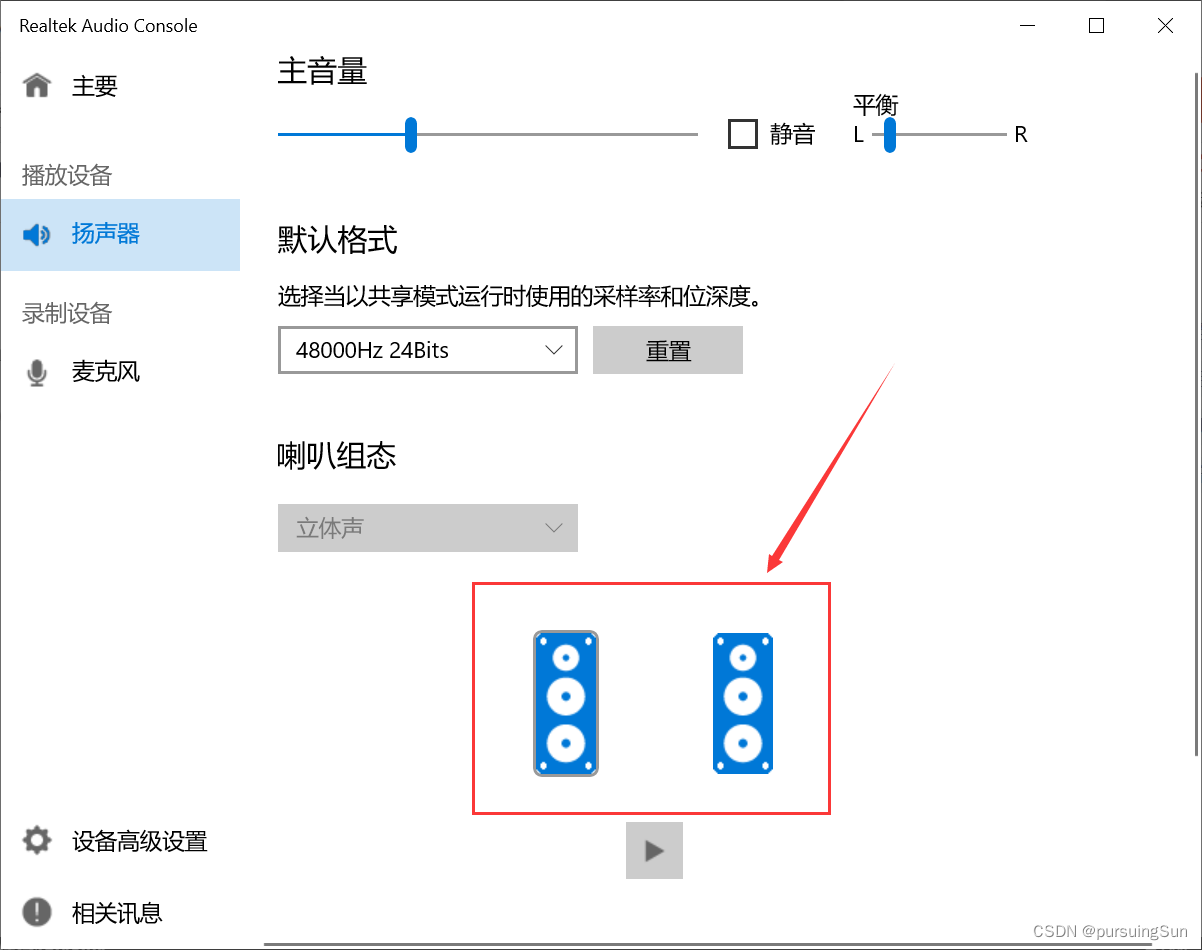
win10电脑插入耳机,右边耳机声音比左边小很多
最近使用笔记本看视频,发现插入耳机(插入式和头戴式)后,右边耳机声音比左边耳机声音小很多很多,几乎是一边很清晰,另一边什么都听不到。 将耳机插到别人电脑上测试耳机正常,那就是电脑的问题。试…...

本文整理了Debian 11在国内的几个软件源。
1.使用说明 一般情况下,将/etc/apt/sources.list文件中Debian默认的软件仓库地址和安全更新仓库地址修改为国内的镜像地址即可,比如将deb.debian.org和security.debian.org改为mirrors.xxx.com,并使用https访问,可使用…...

2023NOIP A层联测6 数点
题目大意 给你一个排列 p p p,对于每一个 i i i,我们在平面上,放置一个点 ( i , p i ) (i,p_i) (i,pi)。对于坐标上下限都在 1 ∼ n 1\sim n 1∼n内的全体 ( n ( n 1 ) 2 ) 2 (\frac{n(n1)}{2})^2 (2n(n1))2矩形,求每个矩形…...
Jmeter 链接MySQL测试
1.环境部署 1.1官网下载MySQL Connector https://dev.mysql.com/downloads/connector/j/ 1.2 解压后,将jar放到jmeter/lib目录下 1.3 在测试计划中添加引用 2.脚本设置 2.1设置JDBC Connection Configuration 先添加一个setUp线程中,在setUp中添加“…...

jwt的了解和使用以及大致代码分析
jwt简介 以下介绍来自官网(https://jwt.io/) SON Web 令牌 (JWT) 是一种开放标准 (RFC 7519),它定义了一种紧凑且独立的方式,用于在各方之间以 JSON 对象的形式安全地传输信息。此信…...

uniapp中videojs、renderjs的使用
在uniapp中使用了某些前端库或iframe,需要操作这些库中的dom的时候, 而uni上又没有document等基础对象。也就无法操作这些dom去实现一些交互逻辑,那么,涉及到这些的前端类库就无法使用,例如html2、canvas、image、vide…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
