动手学强化学习第2章多臂老虎机
2.1简介
多臂老虎机问题可以被看作简化版的强化学习问题。但是其只有动作和奖励没有状态信息,算是简化版的强化学习问题。
2.2问题介绍
2.2.1问题定义
在多臂老虎机(MAB)问题中,有一个有K根拉杆的老虎机,拉动每一根拉杆都对应一个关于奖励的概率分布 R R R。我们每次拉动其中一根拉杆,就可以从该拉杆对应的奖励概率分布中获得一个奖励 r r r。
我们在各个拉杆的奖励概率分布未知的情况下,从头尝试,目标是操作T次拉杆后获得尽可能高的累积奖励。
由于奖励的概率分布是未知的,所以我们需要在探索拉杆的获奖概率和根据经验选择获奖最多的拉杆中进行权衡。采用怎样的操作策略才能使获得的累积奖励最高便是多臂老虎机问题。

2.2.2形式化描述
多臂老虎机问题可以表示为一个元组 < A , R > <A,R> <A,R>,其中:
- A为动作集合,其中一个动作表示拉动一个拉杆。若多臂老虎机一共有K根拉杆,那动作空间就是集合,我们用 a t ∈ A a_t\in A at∈A表示任意一个动作
- R为奖励概率分布,拉动每一根拉杆的动作a都对应一个奖励概率分布R(r|a),不同拉杆的奖励分布通常是不同的。
假设每个时间步只能拉动一个拉杆,多臂老虎机的目标为最大化一段时间步T内累积的奖励: m a x ∑ t = 1 T r t , r t ∼ R ( ⋅ ∣ a t ) max \sum\limits_{t=1}^Tr_t,r_{t} \sim R(\cdot|a_t) maxt=1∑Trt,rt∼R(⋅∣at),其中 a t a_t at表示在第t时间步拉动某一拉杆的动作, r t r_t rt表示动作 a t a_t at获得的奖励。
在 r t ∼ R ( ⋅ ∣ a t ) r_t ∼ R(·|a_t) rt∼R(⋅∣at) 中,符号 ⋅ · ⋅ 表示一个占位符,通常用来表示条件概率的输入或条件。在这个上下文中,它表示奖励 r t r_t rt 是从奖励分布 R 中根据条件 a t a_t at 抽取的。也就是说,它指代了在给定动作 a t a_t at 的条件下,奖励 r t r_t rt 的分布。
这种表示方法用于表达随机性和条件性概率分布,它告诉我们奖励 r t r_t rt 是依赖于代理选择的动作 a t a_t at 而发生的,不同的动作可能导致不同的奖励分布。这对于解释多臂老虎机问题中的随机性和条件性关系非常有用。
2.2.3累积懊悔
对于每一个动作a,我们定义其期望奖励为 Q ( a ) = E r ∼ R ( ⋅ ∣ a ) [ r ] Q(a)=\mathbb{E}_{r \sim R(\cdot|a)}[r] Q(a)=Er∼R(⋅∣a)[r],于是,至少存在一根拉杆,它的期望奖励不小于拉动其他任意一根拉杆,我们将该最优期望奖励表示为 Q ∗ = m a x a ∈ A Q ( a ) Q^*=max_{a\in A}Q(a) Q∗=maxa∈AQ(a)。为了更加直观、方便地观察拉动一根拉杆的期望奖励离最优拉杆期望奖励的差距,我们引入懊悔(regret)概念。
懊悔定义为拉动当前拉杆的动作a与最优拉杆的期望奖励差,即 R ( a ) = Q ∗ − Q ( a ) R(a)=Q^*-Q(a) R(a)=Q∗−Q(a)。
累积懊悔(cumulative regret)即操作T次拉杆后累积的懊悔总量,对于一次完整的T步决策 { a 1 , a 2 , . . . , a T } \{a_1,a_2,...,a_T\} {a1,a2,...,aT},累积懊悔为 σ R = ∑ t = 1 T R ( a t ) \sigma_R=\sum\limits_{t=1}^TR(a_t) σR=t=1∑TR(at),MAB问题的目标为最大化累积奖励,等价于最小化累积懊悔。
符号 E \mathbb{E} E 表示数学期望(Expectation),而不带修饰的 “E” 通常用于表示一般的期望值。它们之间的区别在于:
- E \mathbb{E} E:这是一种数学符号,通常用于表示数学期望操作。在LaTeX等数学标记系统中, E \mathbb{E} E通常用于表示数学期望,表示对随机变量的期望值。数学期望是一个用于描述随机变量平均值的概念。通常,数学期望表示为:
E [ X ] \mathbb{E}[X] E[X]
其中,X 是随机变量, E [ X ] \mathbb{E}[X] E[X] 表示随机变量 X 的期望值。- E:这是字母 “E” 的一般表示,可能用于表示其他数学或物理概念中的变量或符号,不一定表示数学期望。如果没有明确的上下文或标记,它可能表示其他概念,而不是期望操作。
所以, E \mathbb{E} E 是专门用于表示数学期望的符号,而 “E” 可能用于其他用途。当你看到 E [ X ] \mathbb{E}[X] E[X],它明确表示对随机变量 X 的数学期望,而 “E” 会根据上下文的不同而有不同的含义。
Q ( a ) = E r ∼ R ( ⋅ ∣ a ) [ r ] Q(a)=\mathbb{E}_{r \sim R(\cdot|a)}[r] Q(a)=Er∼R(⋅∣a)[r]这个方程表示了动作值函数 Q(a) 的定义,其中 Q(a) 表示对动作 a 的期望奖励值。让我来解释它:
- Q ( a ) Q(a) Q(a):这是动作值函数,表示选择动作 a 后的期望奖励值。动作值函数告诉代理在选择特定动作 a 时,可以预期获得多少奖励。
- E r ∼ R ( ⋅ ∣ a ) [ r ] \mathbb{E}_{r \sim R(\cdot|a)}[r] Er∼R(⋅∣a)[r]:这是期望操作,表示对随机变量 r 的期望,其中 r 来自奖励分布 R(·|a)。这个期望操作告诉我们,在给定动作 a 的情况下,随机抽取的奖励 r 的期望值。
具体来说, Q ( a ) Q(a) Q(a) 是在选择动作 a 后,从奖励分布 R(·|a) 中随机抽取奖励 r 并计算其期望值的结果。这是一种在强化学习中用于估计动作的价值的常见方法。代理使用动作值函数来指导其决策,选择具有最高动作值的动作,以最大化累积奖励。
2.2.4估计期望奖励
为了知道拉动哪一根拉杆能获得更高的奖励,我们需要估计拉动这跟拉杆的期望奖励。由于只拉动一次拉杆获得的奖励存在随机性,所以需要多次拉动一根拉杆,然后计算得到的多次奖励的期望,其算法流程如下所示。
- 对与 ∀ a ∈ A \forall a \in A ∀a∈A,初始化计数器 N ( a ) = 0 N(a)=0 N(a)=0和期望奖励估值 Q ^ ( a ) = 0 \hat Q(a)=0 Q^(a)=0
- for t = 1 → T t=1 →T t=1→Tdo
- 选取某根拉杆,该动作记为 a t a_t at
- 得到奖励 r t r_t rt
- 更新计数器: N ( a t ) = N ( a t ) + 1 N(a_t)=N(a_t)+1 N(at)=N(at)+1
- 更新期望奖励估值: Q ^ ( a t ) = Q ^ ( a t ) + 1 N ( a t ) [ r t − Q ^ ( a t ) ] \hat Q(a_t)=\hat Q(a_t)+\frac{1}{N(a_t)}[r_t-\hat Q(a_t)] Q^(at)=Q^(at)+N(at)1[rt−Q^(at)]
- end for
以上for循环中的第四步如此更新估值,是因为这样可以进行增量式的期望更新,公式如下。
Q k = 1 k ∑ i = 1 k r i = Q_k=\frac{1}{k}\sum\limits_{i=1}^k r_i= Qk=k1i=1∑kri=
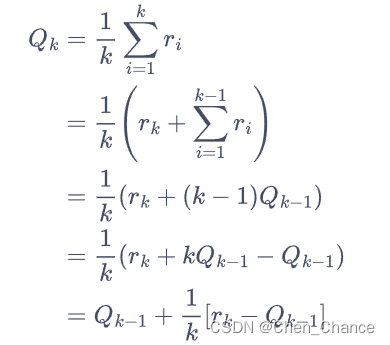
如果将所有数求和再除以次数,其缺点是每次更新的时间复杂度和空间复杂度均为 O ( n ) O(n) O(n)。而采用增量式更新,时间复杂度和空间复杂度均为 O ( 1 ) O(1) O(1)
下面我们编写代码来实现一个拉杆数为 10 的多臂老虎机。其中拉动每根拉杆的奖励服从伯努利分布(Bernoulli distribution),即每次拉下拉杆有p的概率获得的奖励为 1,有1-p的概率获得的奖励为 0。奖励为 1 代表获奖,奖励为 0 代表没有获奖。
# 导入需要使用的库,其中numpy是支持数组和矩阵运算的科学计算库,而matplotlib是绘图库
import numpy as np
import matplotlib.pyplot as pltclass BernoulliBandit:""" 伯努利多臂老虎机,输入K表示拉杆个数 """def __init__(self, K):self.probs = np.random.uniform(size=K) # 随机生成K个0~1的数,作为拉动每根拉杆的获奖概率self.best_idx = np.argmax(self.probs) # 获奖概率最大的拉杆self.best_prob = self.probs[self.best_idx] # 最大的获奖概率self.K = Kdef step(self, k):# 当玩家选择了k号拉杆后,根据拉动该老虎机的k号拉杆获得奖励的概率返回1(获奖)或0(未# 获奖)if np.random.rand() < self.probs[k]:return 1else:return 0np.random.seed(1) # 设定随机种子,使实验具有可重复性
K = 10
bandit_10_arm = BernoulliBandit(K)
print("随机生成了一个%d臂伯努利老虎机" % K)
print("获奖概率最大的拉杆为%d号,其获奖概率为%.4f" %(bandit_10_arm.best_idx, bandit_10_arm.best_prob))
随机生成了一个10臂伯努利老虎机
获奖概率最大的拉杆为1号,其获奖概率为0.7203
相关文章:
动手学强化学习第2章多臂老虎机
2.1简介 多臂老虎机问题可以被看作简化版的强化学习问题。但是其只有动作和奖励没有状态信息,算是简化版的强化学习问题。 2.2问题介绍 2.2.1问题定义 在多臂老虎机(MAB)问题中,有一个有K根拉杆的老虎机,拉动每一根拉杆都对应一个关于奖励…...

钡铼BL124EC实现EtherCAT转Ethernet/IP的优势
钡铼技术的BL124EC是一款用于将EtherCAT从站转换为Ethernet/IP从站的网关设备。它是钡铼技术开发的高性能、可靠的工业自动化通信解决方案之一。 添加图片注释,不超过 140 字(可选) BL124EC网关可以应用于多种工业自动化场景,以下…...

使用IntelliJ Idea必备的插件!
趁手的工具让开发事半功倍,好用的IDEA插件让效率加倍。 今天给大家分享几个优秀的IDEA插件。 插件安装 首先得知道在IDEA哪安装插件? 点击File---->Settings---->找到Plugins标签,即可搜索想要的插件进行安装了。 现在来看下有哪些值…...

代码随想录算法训练营第23期day19| 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
目录 一、(leetcode 654)最大二叉树 二、(leetcode 617)合并二叉树 三、(leetcode 700)二叉搜索树中的搜索 四、(leetcode 98)验证二叉搜索树 一、(leetcode 654&…...
 459. 重复的子字符串)
第四章 字符串part02 28. 实现strStr() 459. 重复的子字符串
第四章 字符串part02 28. 实现strStr() 459. 重复的子字符串 一、28. 实现strStr() 题目链接:https://leetcode.cn/problems/repeated-substring-pattern/ 题目介绍: 给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。…...
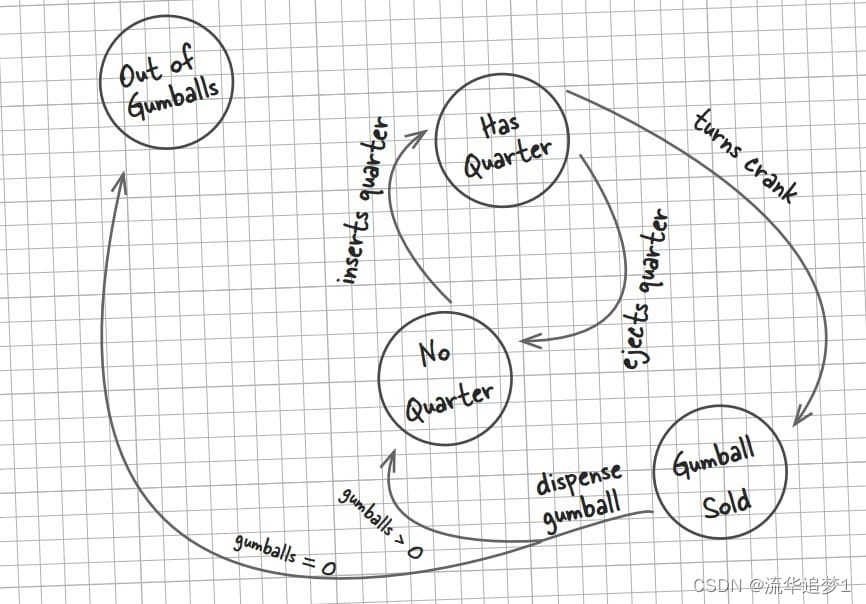
设计模式 - 状态模式
目录 一. 前言 二. 实现 一. 前言 状态模式(State Pattern):它主要用来解决对象在多种状态转换时,需要对外输出不同的行为的问题。状态和行为是一一对应的,状态之间可以相互转换。当一个对象的内在状态改变时&#x…...

【vim 学习系列文章 9 -- .vim 脚本文件开发学习】
文章目录 .vimrc 介绍.vim 脚本文件开发 .vimrc 介绍 在Vim中,你可以将一系列的Vim命令和设置写入一个脚本文件中,并使用:source命令来运行它。这种脚本文件通常被称为vimrc文件,因为它的默认名称是.vimrc。通常,我们将这个文件放…...

NAT模式和桥接模式的区别
NAT模式和桥接模式的区别 NAT模式和桥接模式都是虚拟机网络配置的两种方式,主要区别在于虚拟机与外部网络交互的方式不同。 NAT(Network Address Translation,网络地址转换)模式:在这种模式下,虚拟机和宿主…...

应对出海安全合规挑战,兆珑科技为什么选择了亚马逊云科技?
在中国企业出海进程中,安全合规是企业面临的首要挑战。尤其是当企业业务涉及金融相关领域时,面临着最为严苛的安全合规要求。 深圳兆珑科技有限公司是一家全球化的物联网生态企业,其业务覆盖100多个国家和地区,在欧洲、南美、亚太…...
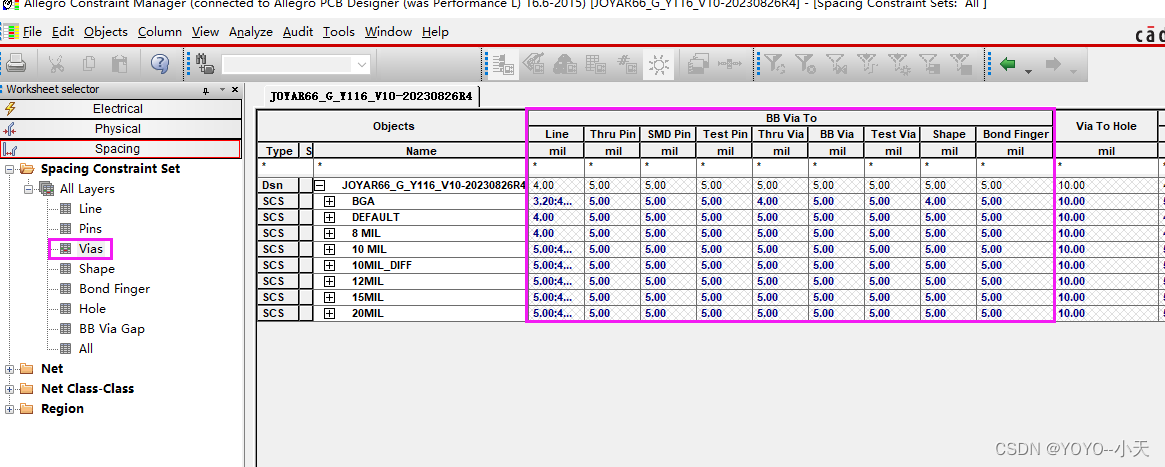
Allegro基本规则设置指导书之Spacing规则设置
进入规则设置界面 1.设置Line 到其他的之间规则: 2.设置Pins 到其他的之间规则: 3.设置Vias 到其他的之间规则:...
使用【Blob、Base64】两种方式显示【文本、图片、视频】 使用 video 组件播放视频
Blob 显示 Blob 对象的类型是由 MIME 类型(Multipurpose Internet Mail Extensions)来确定的。MIME 类型是一种标准,用于表示文档、图像、音频、视频等多媒体文件的类型。以下是一些常见的 Blob 对象类型: text/plain࿱…...

深度学习_1_基本语法
数据结构 代码: import torchx torch.arange(12)##产生长度为12的一维张量print(x)##X x.resize(3, 4)##被弃用##print(X)y torch.reshape(x, (3, 4))##修改向量为矩阵,一维变二维print(y)print(y.size())xx torch.zeros((2, 3, 4))##三维矩阵&…...
c#设计模式-行为型模式 之 中介者模式
🚀简介 又叫调停模式,定义一个中介角色来封装一系列对象之间的交互,使原有对象之间的耦合松散,且可以独立地改变它们之间的交互。 从下右图中可以看到,任何一个类的变 动,只会影响的类本身,以及…...
小程序uView2.X框架upload组件上传方法总结+避坑
呈现效果: 1.1单图片上传 1.2多图片上传 前言:相信很多人写小程序会用到uView框架,总体感觉还算OK吧,只能这么说,肯定也会遇到图片视频上传,如果用到这个upload组件相信你,肯定遇到各种各样的问题,这是我个人总结的单图片和多图片上传方法. uView2.X框架:uView 2.0 - 全面兼容…...

人脸检测及追踪回顾
轻量级人脸检测 代码地址 人脸追踪 代码地址 MNN框架部署文档 文档地址...

虚拟环境和包
目录 12. 虚拟环境和包 12.1. 简介 12.2. 创建虚拟环境 12.3. 使用 pip 管理包 12. 虚拟环境和包 12.1. 简介 Python 应用程序经常会使用一些不属于标准库的包和模块。应用程序有时候需要某个特定版本的库,因为它需要一个特定的 bug 已得到修复的库或者它是使用…...
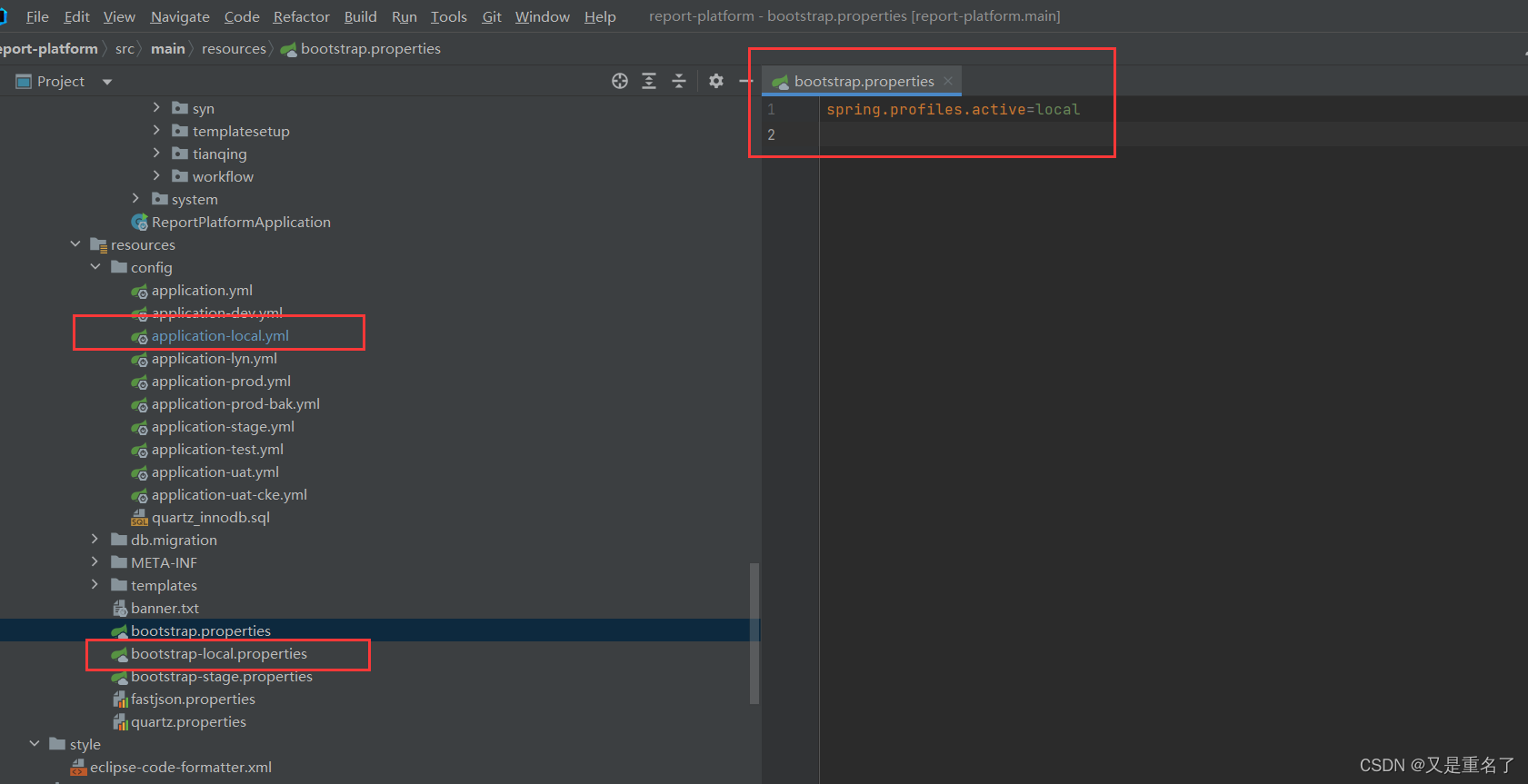
springboot配置文件读取
项目配置文件 怎么说呢,给了个项目,他启动了,然后我看不懂为啥能够启动项目这样 很迷茫,为啥能够成功启动呢项目,为啥项目有properties也要有yml呢? 问题处理 首先,properties的配置的优先级…...

纵享丝滑!Cesium + ffmpegserver 生成高质量动态视频【逐帧生成】
工作中需要提供一些在三维场景下的视频动画素材,屏幕录制会出现掉帧等其他问题,看到 ffmpegserver 后,眼前一亮 Cesium ffmpegserver 生成高质量视频 1.自建 ffmpegserver 首先,克隆 ffmpegserver 仓库代码 git clone https://…...

Linux下C++编程-进度条
引言:本篇主要在linux下的C实现进度条的功能。按照多文件编程,同时使用Makefile文件完成多文件的编译、连接。 首先创建头文件: 1. progress.h #pragma once #include <iostream> #include <cstring> #include <iomanip>…...

C语言常见题目(1)交换两个变量的值,数的逆序输出,猜数游戏,两个数比较大小等
我的个人主页:☆光之梦☆的博客_CSDN博客-C语言基础语法(超详细)领域博主 欢迎各位 👍点赞 ⭐收藏 📝评论 特别标注:本博主将会长期更新c语言的语法知识,初学c语言的朋友们,可以收藏…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
