Fisher辨别分析
- 问题要求
在UCI数据集上的Iris和Sonar数据上验证算法的有效性。训练和测试样本有三种方式(三选一)进行划分:
(一) 将数据随机分训练和测试,多次平均求结果
(二)K折交叉验证
(三)留1法
针对不同维数,画出曲线图。
- 问题分析
(一)数据集
1.Iris数据集是常用的分类实验数据集,由Fisher收集整理。Iris也称鸢尾花卉数据集,是一类多重变量分析的数据集。数据集包含150个数据样本,分为3类,每类50个数据,每个数据包含4个属性。可通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa,Versicolour,Virginica)三个种类中的哪一类。
2.在Sonar数据集中有两类(字母“R”(岩石)和“M”(矿井)),分别有97个和111个数据,每个数据有60维的特征。这个分类任务是为了判断声纳的回传信号是来自金属圆柱还是不规则的圆柱形石头。
(二)Fisher线性判别分析
1.方法总括
Fisher线性判别方法可概括为把 d 维空间的样本投影到一条直线上,形成一维空间,即通过降维去解决两分类问题。如何根据实际数据找到一条最好的、最易于分类的投影方向,是 Fisher 判别方法所要解决的基本问题。
2. 求解过程
(1)核心思想
假设有一集合 D 包含 m 个 n 维样本{x1, x2, …, xm},第一类样本集合记为 D1,规模为 N1,第二类样本集合记为 D2,规模为 N2。若对 xi 的分量做线性组合可得标量:yi = wTxi(i=1,2,…,m)这样便得到 m 个一维样本 yi 组成的集合, 并可分为两个子集 D’1 和 D’2。计算阈值 yo,当 yi>yo 时判断 xi 属于第一类, 当 yi<yo 时判断 xi 属于第二类,当 yi=yo 时 xi 可判给任何一类或者拒收。(2)具体推导
相关书籍或网站上都有具体推导过程,这里不再赘述。
(3)样本划分
采用留1法划分训练集和数据集,该方法是K折法的一种极端情况。
在K折法中,将全部训练集 S分成 k个不相交的子集,假设 S中的训练样例个数为 N,那么每一个子集有 N/k 个训练样例,相应的子集称作 {s1,s2,…,sk}。每次从分好的子集中里面,拿出一个作为测试集,其它k-1个作为训练集,根据训练训练出模型或者假设函数。然后把这个模型放到测试集上,得到分类率,计算k次求得的分类率的平均值,作为该模型或者假设函数的真实分类率。
当取K的值为样本个数N时,即将每一个样本作为测试样本,其它N-1个样本作为训练样本。这样得到N个分类器,N个测试结果。用这N个结果的平均值来衡量模型的性能,这就是留1法。在UCI数据集中,由于数据个数较少,采用留一法可以使样本利用率最高。
- 仿真结果
- 1.Iris数据集
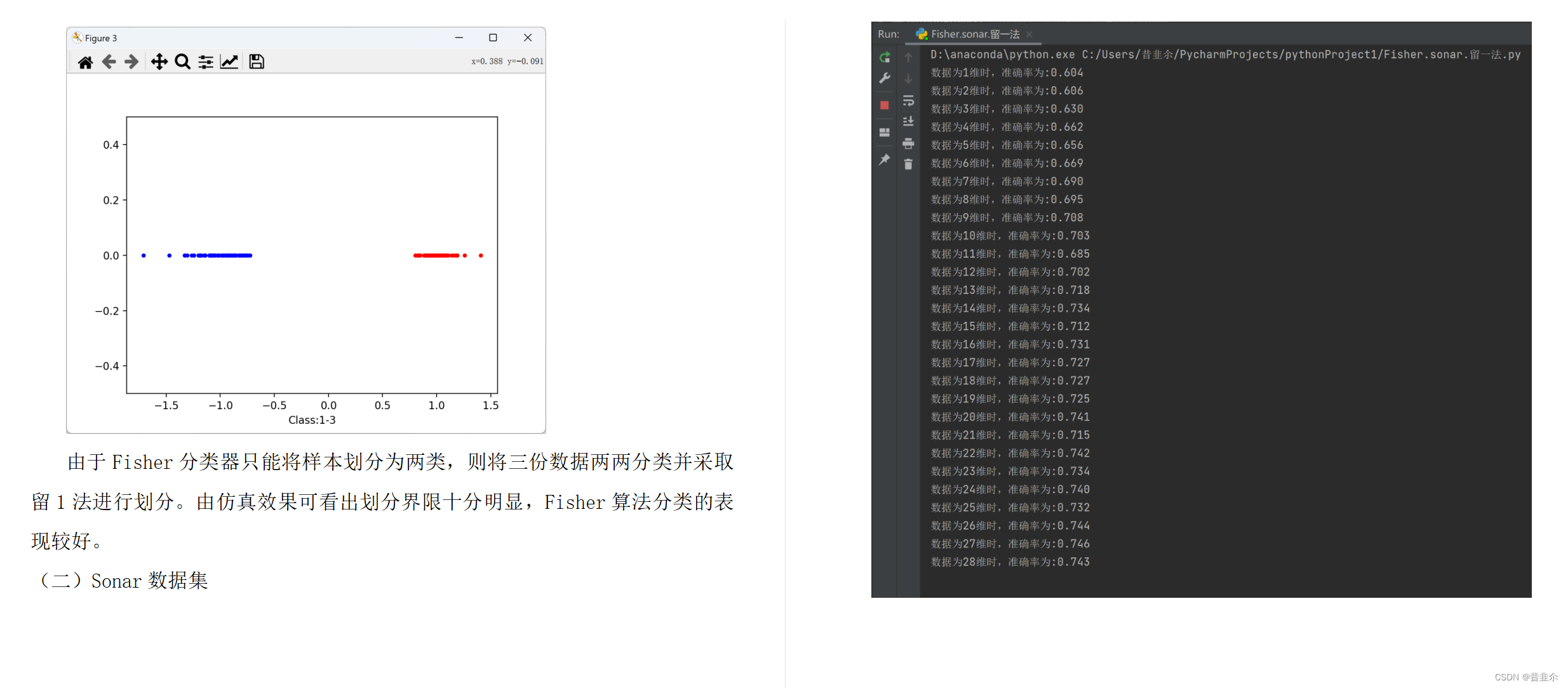
由于Fisher分类器只能将样本划分为两类,则将三份数据两两分类并采取留1法进行划分。由仿真效果可看出划分界限十分明显,Fisher算法分类的表现较好。
- 2.Sonar数据集
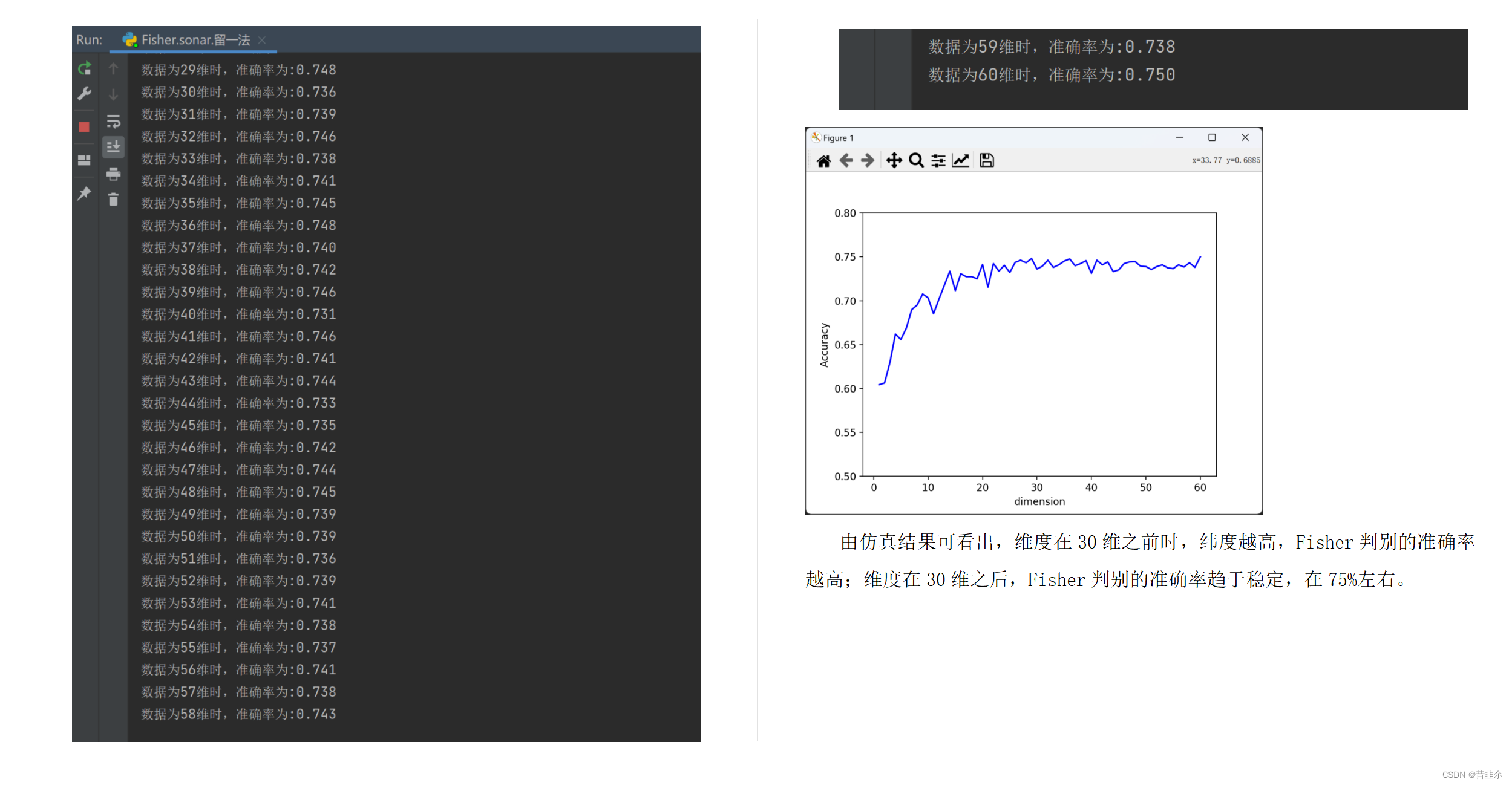
由仿真结果可看出,维度在30维之前时,纬度越高,Fisher判别的准确率越高;维度在30维之后,Fisher判别的准确率趋于稳定,在75%左右。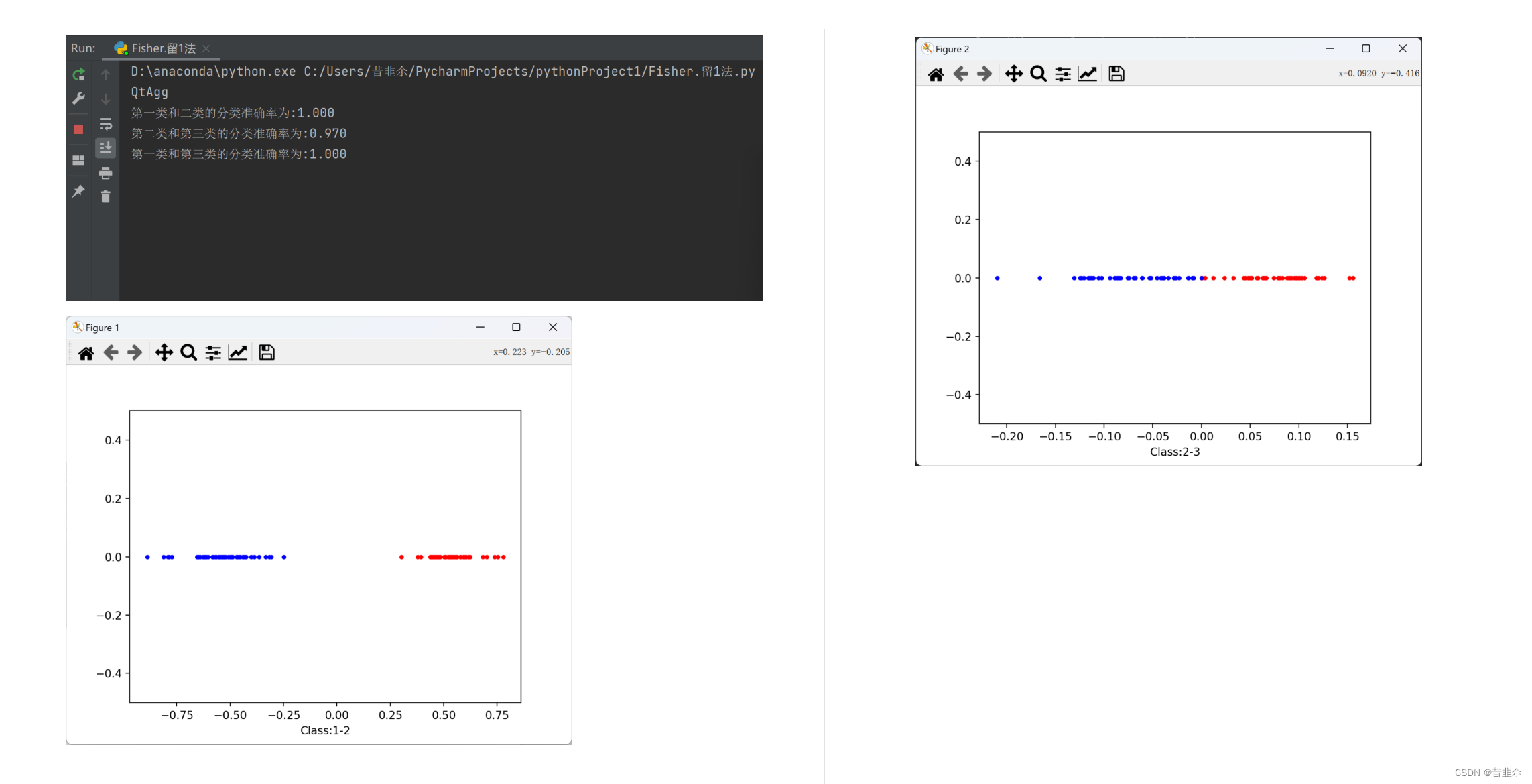
代码如下:
(1)iris数据集
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
print(mpl.get_backend())Iris = pd.read_csv('iris.data', header=None, sep=',')def Fisher(X1, X2, t):# 各类样本均值向量m1 = np.mean(X1, axis=0)m2 = np.mean(X2, axis=0)m1 = m1.reshape(4, 1)m2 = m2.reshape(4, 1)m = m1 - m2# 样本类内离散度矩阵s1 = np.zeros((4, 4)) # s1,s2此时均为数组s2 = np.zeros((4, 4))if t == 0: # 第一种情况for i in range(0, 49):s1 += (X1[i].reshape(4, 1) - m1).dot((X1[i].reshape(4, 1) - m1).T)for i in range(0, 50):s2 += (X2[i].reshape(4, 1) - m2).dot((X2[i].reshape(4, 1) - m2).T)if t == 1: # 第二种情况for i in range(0, 50):s1 += (X1[i].reshape(4, 1) - m1).dot((X1[i].reshape(4, 1) - m1).T)for i in range(0, 49):s2 += (X2[i].reshape(4, 1) - m2).dot((X2[i].reshape(4, 1) - m2).T)# 总类内离散度矩阵sw = s1 + s2sw = np.mat(sw, dtype='float')m = np.mat(m, dtype='float')# 最佳投影方向w = np.linalg.inv(sw).dot(m)# 在投影后的一维空间求两类的均值m1 = np.mat(m1, dtype='float')m2 = np.mat(m2, dtype='float')m_1 = (w.T).dot(m1)m_2 = (w.T).dot(m2)# 计算分类阈值w0w0 = -0.5 * (m_1 + m_2)return w, w0def Classify(X,w,w0):y = (w.T).dot(X) + w0return y#数据预处理
Iris = Iris.iloc[0:150,0:4]
iris = np.mat(Iris)Accuracy = 0iris1 = iris[0:50, 0:4]
iris2 = iris[50:100, 0:4]
iris3 = iris[100:150, 0:4]G121 = np.ones(50)
G122 = np.ones(50)
G131 = np.zeros(50)
G132 = np.zeros(50)
G231 = np.zeros(50)
G232 = np.zeros(50)# 留一法验证准确性
# 第一类和第二类的线性判别
count = 0
for i in range(100):if i <= 49:test = iris1[i]test = test.reshape(4, 1)train = np.delete(iris1, i, axis=0)w, w0 = Fisher(train, iris2, 0)if (Classify(test, w, w0)) >= 0:count += 1G121[i] = Classify(test, w, w0)else:test = iris2[i-50]test = test.reshape(4, 1)train = np.delete(iris2, i-50, axis=0)w, w0 = Fisher(iris1, train, 1)if (Classify(test, w, w0)) < 0:count += 1G122[i-50] = Classify(test, w, w0)
Accuracy12 = count/100
print("第一类和二类的分类准确率为:%.3f"%(Accuracy12))# 第二类和第三类的线性判别
count = 0
for i in range(100):if i <= 49:test = iris2[i]test = test.reshape(4, 1)train = np.delete(iris2, i, axis=0)w, w0 = Fisher(train, iris3, 0)if (Classify(test, w, w0)) >= 0:count += 1G231[i] = Classify(test, w, w0)else:test = iris3[i-50]test = test.reshape(4, 1)train = np.delete(iris3, i-50, axis=0)w, w0 = Fisher(iris2, train, 1)if (Classify(test, w, w0)) < 0:count += 1G232[i-50] = Classify(test, w, w0)
Accuracy23 = count/100
print("第二类和第三类的分类准确率为:%.3f"%(Accuracy23))# 第一类和第三类的线性判别
count = 0
for i in range(100):if i <= 49:test = iris1[i]test = test.reshape(4, 1)train = np.delete(iris1, i, axis=0)w, w0 = Fisher(train, iris3, 0)if (Classify(test, w, w0)) >= 0:count += 1G131[i] = Classify(test, w, w0)else:test = iris3[i-50]test = test.reshape(4, 1)train = np.delete(iris3, i-50, axis=0)w,w0 = Fisher(iris1, train, 1)if (Classify(test, w, w0)) < 0:count += 1G132[i-50] = Classify(test, w, w0)
Accuracy13 = count/100
print("第一类和第三类的分类准确率为:%.3f"%(Accuracy13))# 作图
y1 = np.zeros(50)
y2 = np.zeros(50)
plt.figure(1)
plt.ylim((-0.5, 0.5))# 画散点图
plt.scatter(G121, y1, color='red', marker='.')
plt.scatter(G122, y2, color='blue', marker='.')
plt.xlabel('Class:1-2')
plt.show()plt.figure(2)
plt.ylim((-0.5, 0.5))
# 画散点图
plt.scatter(G231, y1, c='red', marker='.')
plt.scatter(G232, y2, c='blue', marker='.')
plt.xlabel('Class:2-3')
plt.show()plt.figure(3)
plt.ylim((-0.5, 0.5))
# 画散点图
plt.scatter(G131, y1, c='red', marker='.')
plt.scatter(G132, y2, c='blue', marker='.')
plt.xlabel('Class:1-3')
plt.show()(2)Sonar数据集
import numpy
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltpath=r'sonar.all-data.txt'
df = pd.read_csv(path, header=None, sep=',')def Fisher(X1, X2, n, t):# 各类样本均值向量m1 = np.mean(X1, axis=0)m2 = np.mean(X2, axis=0)m1 = m1.reshape(n, 1)m2 = m2.reshape(n, 1)m = m1 - m2# 样本类内离散度矩阵s1 = np.zeros((n, n)) # s1,s2此时均为数组s2 = np.zeros((n, n))if t == 0: # 第一种情况for i in range(0, 96):s1 += (X1[i].reshape(n, 1) - m1).dot((X1[i].reshape(n, 1) - m1).T)for i in range(0, 111):s2 += (X2[i].reshape(n, 1) - m2).dot((X2[i].reshape(n, 1) - m2).T)if t == 1: # 第二种情况for i in range(0, 97):s1 += (X1[i].reshape(n, 1) - m1).dot((X1[i].reshape(n, 1) - m1).T)for i in range(0, 110):s2 += (X2[i].reshape(n, 1) - m2).dot((X2[i].reshape(n, 1) - m2).T)# 总类内离散度矩阵sw = s1 + s2sw = np.mat(sw, dtype='float')m = numpy.mat(m, dtype='float')# 最佳投影方向w = np.linalg.inv(sw).dot(m)# 在投影后的一维空间求两类的均值m_1 = (w.T).dot(m1)m_2 = (w.T).dot(m2)# 计算分类阈值w0w0 = -0.5 * (m_1 + m_2)return w, w0def Classify(X,w,w0):y = (w.T).dot(X) + w0return y# 数据预处理
Sonar = df.iloc[0:208,0:60]
sonar = np.mat(Sonar)# 分十次计算准确率
Accuracy = np.zeros(60)
accuracy_ = np.zeros(10)
for n in range(1,61):for t in range(10):sonar_random = (np.random.permutation(sonar.T)).T # 对原sonar数据进行每列打乱sonar1 = sonar_random[0:97, 0:n]sonar2 = sonar_random[97:208, 0:n]count = 0# 留一法验证准确性for i in range(208): # 取每一维度进行测试if i <= 96:test = sonar1[i]test = test.reshape(n, 1)train = np.delete(sonar1, i, axis=0)w, w0 = Fisher(train, sonar2, n, 0)if (Classify(test, w, w0)) >= 0:count += 1else:test = sonar2[i-97]test = test.reshape(n, 1)train = np.delete(sonar2, i-97, axis=0)w, w0 = Fisher(sonar1, train, n, 1)if (Classify(test, w, w0)) < 0:count += 1accuracy_[t] = count / 208for k in range(10):Accuracy[n - 1] += accuracy_[k]Accuracy[n - 1] = Accuracy[n - 1] / 10print("数据为%d维时,准确率为:%.3f" % (n, Accuracy[n - 1]))# 作图
x = np.arange(1, 61, 1)
plt.xlabel('dimension')
plt.ylabel('Accuracy')
plt.ylim((0.5, 0.8)) # y坐标的范围
plt.plot(x, Accuracy, 'b')
plt.show()相关文章:

Fisher辨别分析
问题要求 在UCI数据集上的Iris和Sonar数据上验证算法的有效性。训练和测试样本有三种方式(三选一)进行划分: (一) 将数据随机分训练和测试,多次平均求结果 (二)K折交叉验证 &…...
【Zookeeper专题】Zookeeper选举Leader源码解析
目录 前言阅读建议课程内容一、ZK Leader选举流程回顾二、源码流程图三、Leader选举模型图 学习总结 前言 为什么要看源码?说实在博主之前看Spring源码之前没想过这个问题。因为我在看之前就曾听闻大佬们说过【JavaCoder三板斧:Java,Mysql&a…...
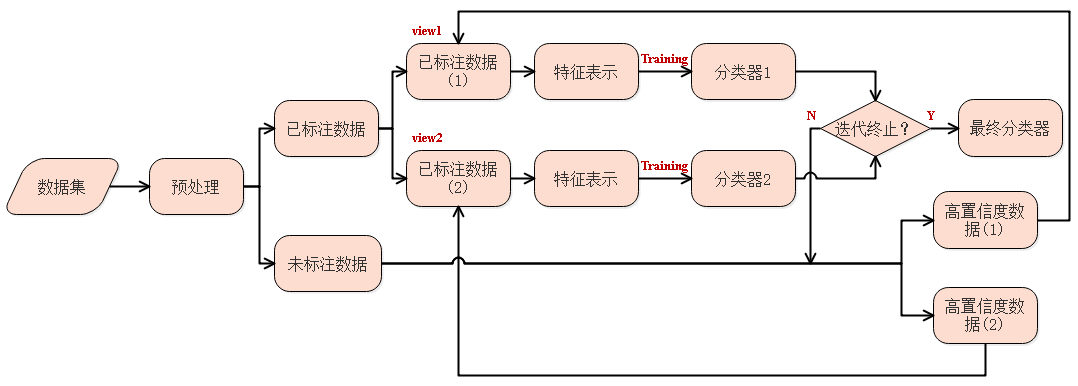
机器学习之自训练协同训练
前言 监督学习往往需要大量的标注数据, 而标注数据的成本比较高 . 因此 , 利用大量的无标注数据来提高监督学习的效果有着十分重要的意义. 这种利用少量标注数据和大量无标注数据进行学习的方式称为 半监督学习 ( Semi…...

ubuntu 通过apt-get快速安装 docker
在使用 apt-get 安装 Docker 之前,你需要确保你的系统已经准备好并且已经更新了软件包列表。以下是在 Ubuntu 系统上使用 apt-get 安装 Docker 的步骤: 更新软件包列表: sudo apt-get update 安装依赖软件包,以确保可以通过 HTTPS 使用存储库: sudo apt-get install apt-t…...
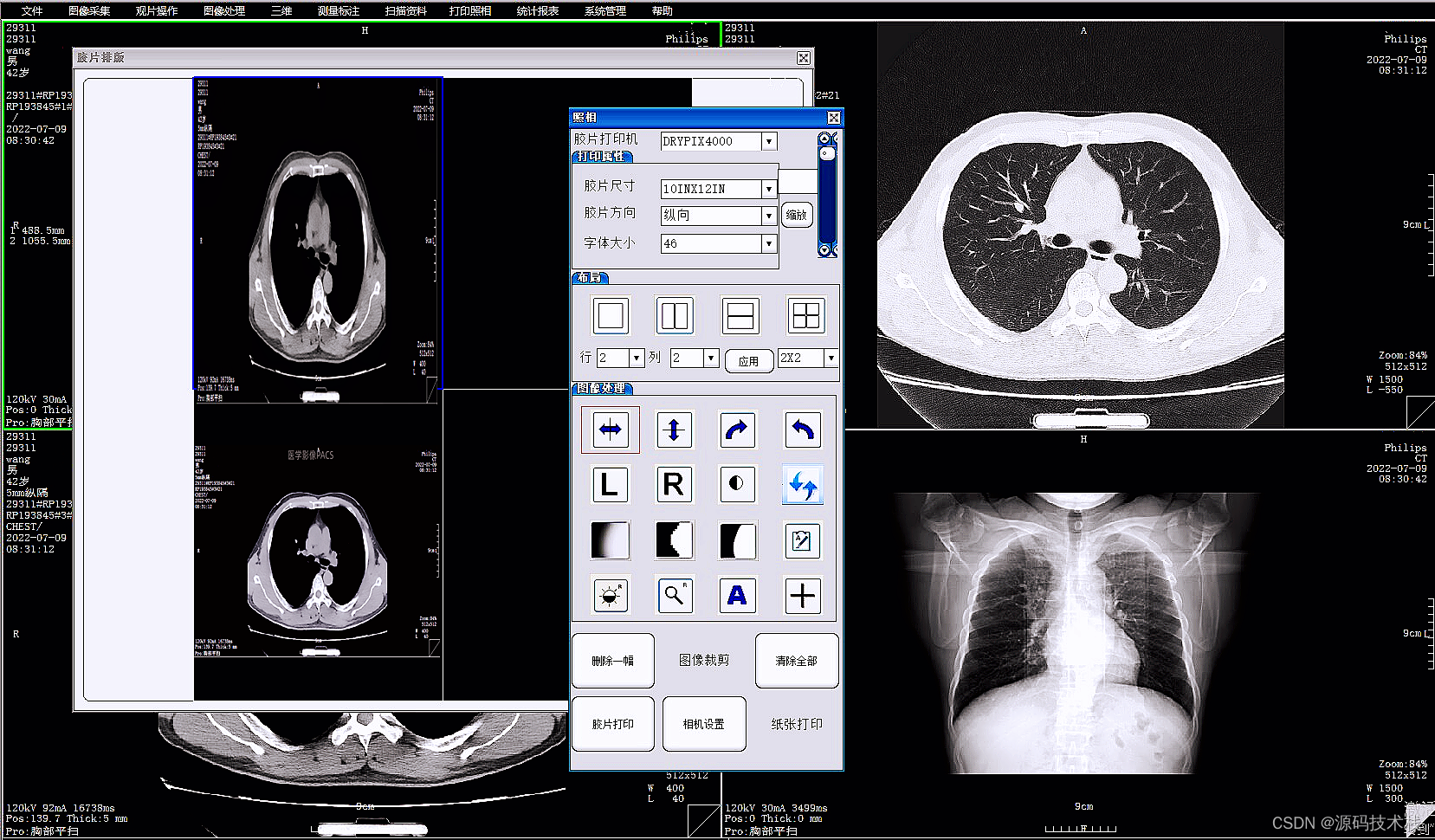
C++医院影像科PACS源码:三维重建、检查预约、胶片打印、图像处理、测量分析等
PACS连接DICOM接口的医疗器械(如CT、MRI、CR、DR、DSA、各种窥镜成像系统设备等),实现图像无损传输,实现DICOM胶片打印机回传打印功能,支持各种图像处理,可以进行窗技术调节,与登记台管理系统共…...

企业聊天应用程序使用 Kubernetes
1. 客户端-服务器工作流程 客户端:在我们的架构中,客户端可以分为三种类型:iOS 和 Android 移动应用程序以及 Web 聊天。移动应用程序首先通过 API 网关服务与服务器进行通信,其中客户端会生成一个访问令牌,该令牌将授…...
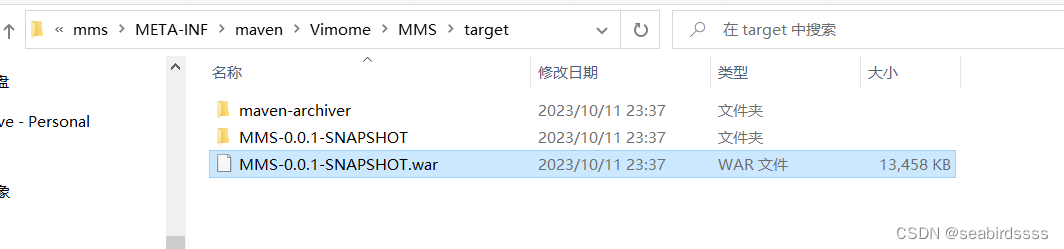
记录用命令行将项目打包成war包
记录用命令行将项目打包成war包 找到项目的pom.xml 在当前路径下进入cmd 输入命令 mvn clean package 发现报错了 Failed to execute goal org.apache.maven.plugins:maven-war-plugin:2.2:war (default-war) on project MMS: Error assembling WAR: webxml attribute is req…...

Linux基础知识笔记
Linux基础知识笔记 介绍/dev/null作用2>&1作用 介绍 记录linux基础知识,持续更新中… /dev/null作用 /dev/null 是一个特殊的设备文件,可以将数据重定向到这个文件中,从而实现将输出或错误信息丢弃的效果。在 Linux 系统中…...

Laya3.0 入门教程
点击play箭头 点击右边的开发者工具 就会弹出 chrome的调试窗口 然后定位到你自己的ts文件 直接在ts里断点即可 不需要js文件 如何自动生成代码? 比如你打开一个新项目 里面显示的是当前场景 只需要点击 UI运行时 右边的框就可以了 他会自动弹窗提示你 创建一个文…...

3D全景虚拟样板间展销系统扩展用户市场范围
VR样板间,能够真实还原现场,定制需要的场景。让一切比真实更真实。用户可以720度看房,自由行走在空间里,直观感受各空间的大小,看到自己家中的“未来样子”,同时通过操控手柄,控制整个智能家居系…...

如何编写lua扩展库
很多人都听过lua,也见过lua脚本,但可能不理解为什么lua脚本里面会有这么多没见过的函数, 而且这些函数功能是如此强大,能上天入地,无所不能 其实这些函数并不是lua自带的,都是由程序作者造出来的隐藏在了他们的主程序里 一般运行lua脚本,我们会使用自带的解释器,当你拿到一份…...
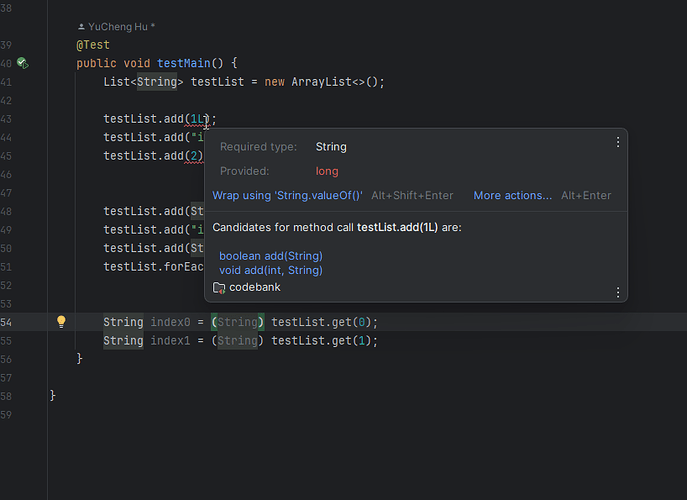
Java List 中存不同的数据类型
在最近的实践中,有人突然问了一个问题: 在 Java 的 List 中可以存不同的数据类型吗? 这个问题突然给问到了,我们都知道 Java 中的 List 中存的是对象,通常我们定义都会这样的定义: List<String> t…...

pyqt5:openpyxl 读取 Excel文件,显示在 QTableWidget 中
pip install openpyxl openpyxl-3.1.2-py2.py3-none-any.whl (249 kB) et_xmlfile-1.1.0-py3-none-any.whl (4.7 kB) 摘要:A Python library to read/write Excel 2010 xlsx/xlsm files pip install pyqt5; pip install pyqt5-tools; 编写 openpyxl_pyqt5.py 如…...

在RabbitMQ中使用新的MQTT 5.0功能
MQTT是物联网(IoT)的标准协议,是轻量级的,协议头很小,可以节省网络带宽。MQTT也很有效,与其他消息传递协议相比,客户端通过更短的握手进行连接和身份验证。 以下是本文介绍的MQTT 5.0功能列表&…...

flinkcdc 体验
0 flink版本 踩雷 java代码操作 flink Table/SQL API 和 DataStream API 编写程序后,打成jar包丢到flink集群运行,报错首选需要考虑flink集群版本和 jar包中maven依赖的版本是否一致。 目前网上flink、flinkcdc相关博文绝大部分是基于flink1.13、1.14编…...

Kafka知识补充
如何避免 Rebalance 最简单粗暴的就是 : 减少组成员数量发生变化 每个 Consumer 实例都会定期地向 Coordinator 发送心跳请求,表明它还存活着。如果某个 Consumer 实例不能及时地发送这些心跳请求,Coordinator 就会认为该 Consumer 已经“死…...

【MAC】升级 Mac os 后报错
背景 17 年买的 mac,发现很多软件都无法安装,于是升级 mac os 到 10.13,从官网下载 10.13 版本,之后升级,升级还算顺利。但使用 git 的时候发现出现问题了。 问题 使用 git 出现如下错误 xcrun: error: invalid ac…...

LeetCode(力扣)416. 分割等和子集Python
LeetCode416. 分割等和子集 题目链接代码 题目链接 https://leetcode.cn/problems/partition-equal-subset-sum/ 代码 class Solution:def canPartition(self, nums: List[int]) -> bool:sum 0dp [0]*10001for num in nums:sum numif sum % 2 1:return Falsetarget …...

Redis之缓存一致性
Redis之缓存一致性 1 缓存更新策略1.1 内存淘汰1.2 过期删除1.3 主动更新1.4 三种缓存更新策略的对比 2 更新缓存的两种方式3 缓存更新策略的实现方式3.1 先更新DB,后更新缓存3.2 先更新DB,后删除缓存3.3 先更新缓存,后更新DB3.4 先删除缓存&…...
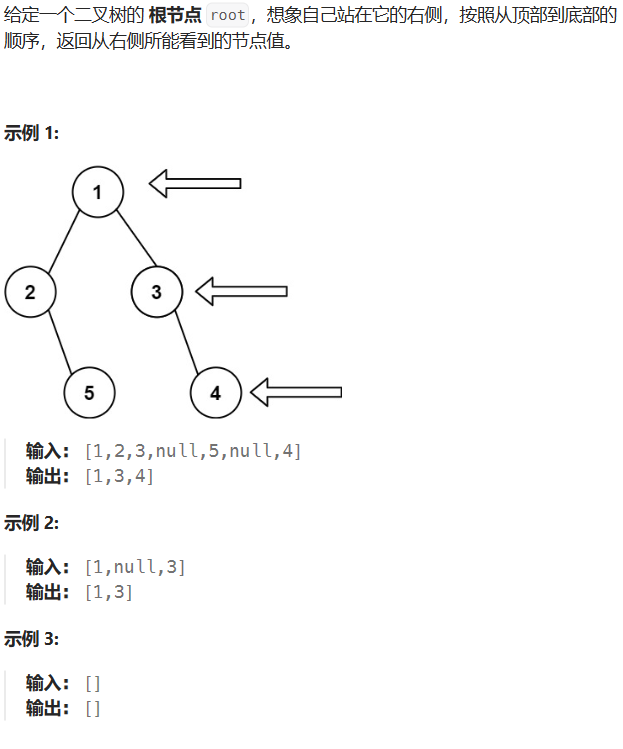
LeetCode-199-二叉树的右视图
题目描述: 题目链接:LeetCode-199-二叉树的右视图 解题思路: 在 102 的基础之上进行改进,一维数组每次只保存 size1 时候的值 代码实现: class Solution {public List<Integer> rightSideView(TreeNode root) {i…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
