python学习笔记2-数字转化为String
题目链接
- str() 强制转换， sorted() 转换为有序列表，join() 将列表中的元素连接到字符串中，然后奇偶位组合成数字
class Solution:def splitNum(self, num: int) -> int:stnum = "".join(sorted(str(num)))num1, num2 = int(stnum[0::2]), int(stnum[1::2])return num1 + num2
相关文章：
python学习笔记2-数字转化为String
题目链接 str() 强制转换， sorted() 转换为有序列表，join() 将列表中的元素连接到字符串中，然后奇偶位组合成数字 class Solution:def splitNum(self, num: int) -> int:stnum "".join(sorted(str(num)))num1, num2 int(stn…...
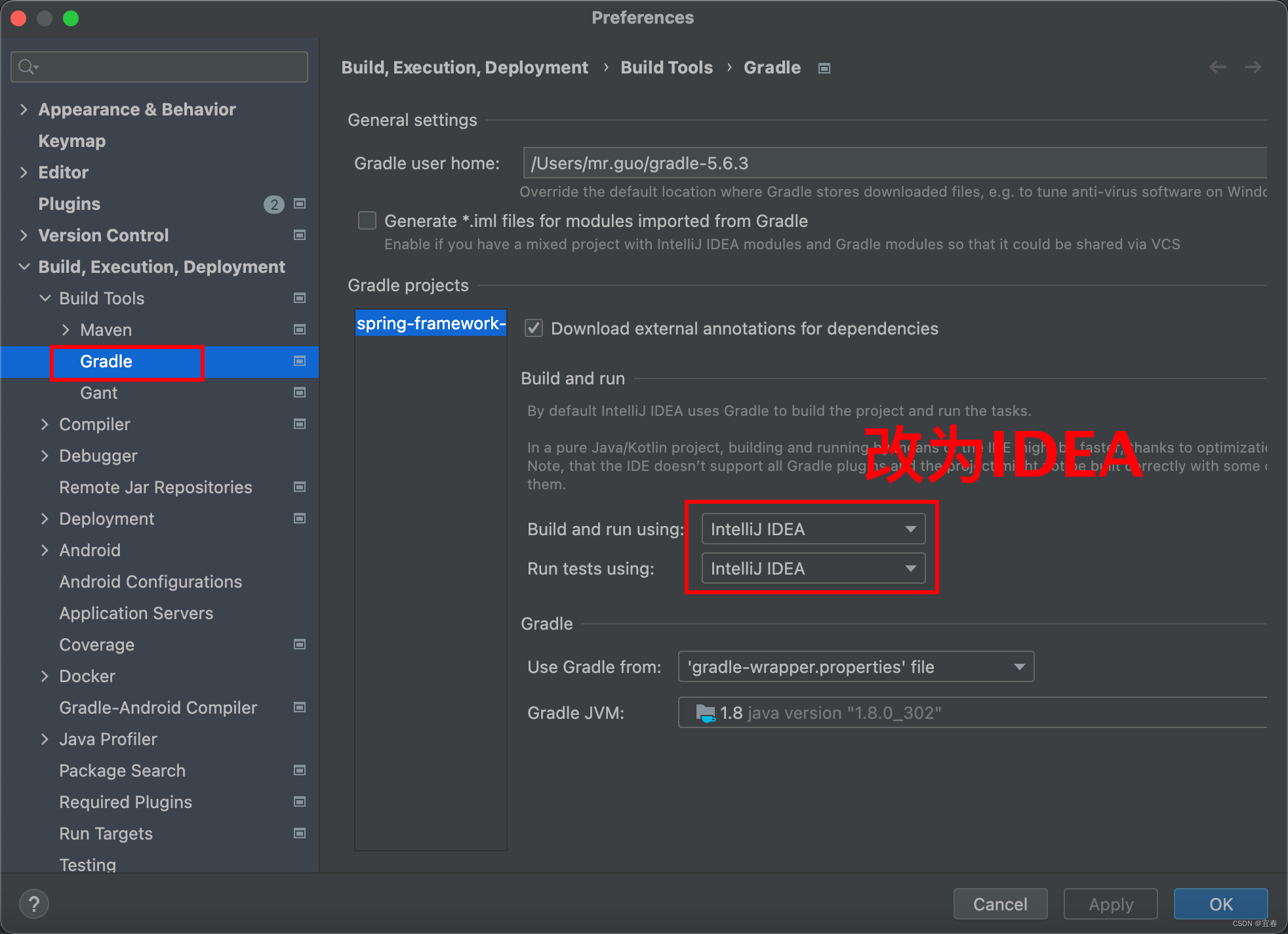
MAC版Gradle构建Spring5.X源码阅读环境
前言： 三年前鄙人有幸在现已几乎报废的Window的DELL中搭建过Spring源码环境，今天，Mac版的搭建，来了。 本篇文章环境搭建：Spring5.2.1 Gradle5.6.3-all jdk8 IDEA2022.3版本 文章目录 1、Spring源码下载2、Gradle下载…...
Linux 常用通配符
通配符是一种特殊语句，主要有星号（*）和问号（？），用来模糊搜索文件。当查找文件夹时，可以使用它来代替一个或多个真正字符；当不知道真正字符或者懒得输入完整名字时&#x…...
Python皮卡丘
系列文章 序号文章目录直达链接1浪漫520表白代码https://want595.blog.csdn.net/article/details/1306668812满屏表白代码https://want595.blog.csdn.net/article/details/1297945183跳动的爱心https://want595.blog.csdn.net/article/details/1295031234漂浮爱心https://want…...
【数据结构与算法】三种简单排序算法，包括冒泡排序、选择排序、插入排序算法
冒泡排序算法 冒泡排序他是通过双重循环对每一个值进行比较，将小的值向后移动，以达到最终排序的结果，他的时间复杂度为O(n^2)。 /*** 冒泡排序* param arr*/public static void bubbleSort(int[] arr){int l arr.length;for (int i 0; i <…...
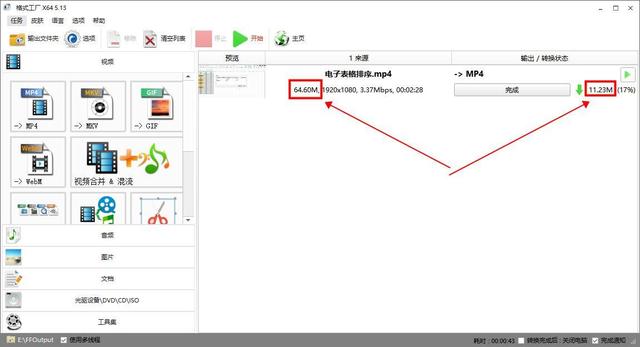
视频太大怎么压缩变小？超过1G的视频这样压缩
视频已经成为了我们日常生活中不可或缺的一部分，然而，很多时候，我们可能会遇到视频文件过大，无法在某些平台上传或保存的问题。那么，如何将过大的视频文件压缩变小呢？ 下面就给大家分享三款实用的工具&…...
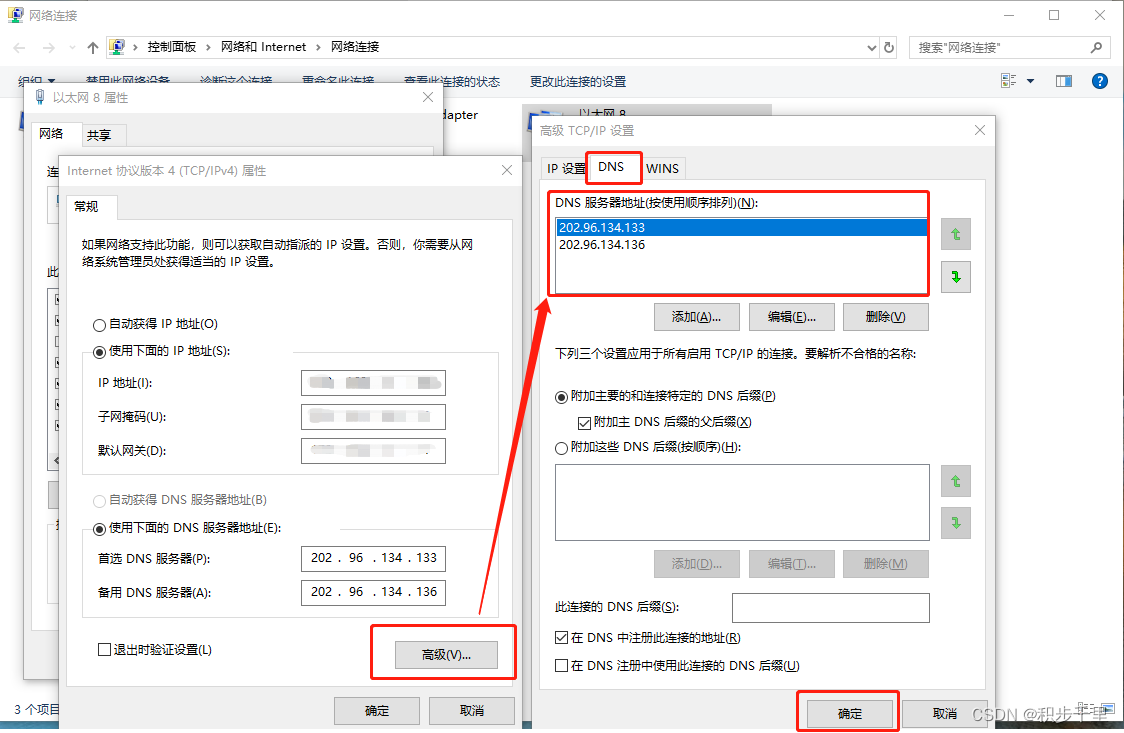
Edge 无法登录/同步问题【一招搞定】
目录 前言 一、打开 Edge 浏览器显示未同步，点击同步无效 二、Edge 登录报错 0x801901f4 或 0x80190001 解决方法 2.1 报错 0x801901f4 解决方法 2.1.0 Edge 登陆报错图示 2.1.1 添加 Edge 推荐的 DNS 地址 2.1.2 重新登录 Edge 账号成功 2.2 报错 0x801…...
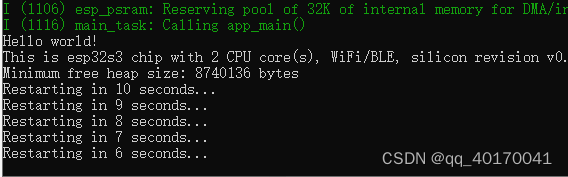
ESP32-S3上手开发
1、搭建开发环境 首先搭建开发环境，这里采用了windows下集成开发环境ide进行开发，具体的安装方法：ESP-IDF安装配置 这里使用的乐鑫的esp32s3，N16R8 2、esp32s3模块 从上面图中可以看到，N16R8这里使用了外扩16M的fl…...
UE4和C++ 开发-编程基础记录（UE4+代码基础知识）
1、UE4基础元素 ①Actor 我们又见面了Actor，Actor是在一个关卡中持续存在的，通常他包含几个Actor组件。支持网络复制和多人游戏。 Actor不包含位置，方向。这些东西在Root Component中存储。对于UE3 中的Pawn也由PlayerCharacter继承了…...
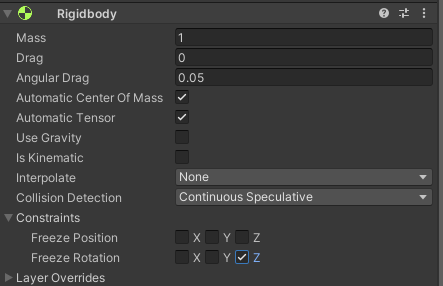
【Unity】【VR】如何让Distance Grab抓取物品时限制物品的Rotation
【背景】 遇到这样的场景，希望抓取Canvas时，Canvas不会沿Z轴旋转。 【问题】 发现Freeze Canvas的Rigid Body没有用。 【分析】 应该是RigidBody的限制仅在物理互动下生效，抓取可能不属于物理互动（比如碰撞），所以不生效。 【思路】 还是得写脚本挂载在Interacta…...
为什么3ds max渲染效果图有噪点？点进来，CG Magic告诉您！
大家在使用3ds max渲染效果图时，可能渲染结果往往会出现的都是不真实，有小伙伴会问如何使3dmax渲染效果图真实呢？ 不真实就算了，渲染过程中，会出现3Dmax渲染噪点多这类问题。 什么原因3ds max渲染效果图有噪点呢&a…...
Element UI怎么安装呢？
安装 :::warning 注意 后续演示将会在 Vue CLI 搭建的 Vue 项目上进行操作。如需要请查看 Vue CLI 安装 ::: 通过 YARN 命令安装 $ yarn add element-ui完整引入 代表一次性引入所有组件，比较省心省事，但是项目的打包体积也会跟着变大。 // main.js…...
redis批量删除命令
./redis-cli -h 127.0.0.1 -p 6379 -n 2 KEYS "170*:redisKeyStr" | xargs ./redis-cli -h 127.0.0.1 -p 6379 -n 2 DEL...
kubernetes环境 搭建
1、准备2台机器 2、安装docker环境（参考官网） 1、 sudo apt-get update sudo apt-get install ca-certificates curl gnupg2、 sudo install -m 0755 -d /etc/apt/keyrings curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo gpg --dea…...
TCP习题总结
1、在采用TCP连接的数据传输阶段，如果发送端的发送窗口值由1000变为2000，那么发送端在收到一个确认之前可以发送（）。 A. 2000个TCP报文段 B. 2000B C. 1000B D. 1000 个 TCP 报文 这道题考察的是TCP的基本…...
华为发布LampSite X室内数字化创新解决方案，释放数字世界无限潜能
【阿联酋，迪拜，2023年10月11日】2023全球移动宽带论坛（Global MBB Forum 2022）期间，华为董事、ICT产品与解决方案总裁杨超斌重磅发布了全新一代5G室内数字化产品解决方案LampSite X系列，助力运营商打开商业…...
麒麟操作系统设置QT程序开机自启动有效方法
在麒麟操作系统上设置QT程序开机自启动的两种简单有效的方法。支持请点赞！ 一、QT程序打包 1.设置环境变量 设置QT和linuxdeployqt的环境变量，已设置可忽略该步骤。 在/etc/profile文件末尾添加一下内容： export PATH/usr/local/Qt-5.15.…...
Python数组删除元素pop与remove对比
pop()和remove()函数都可以用来删除列表中的函数，pop()是按索引来删除的，remove()是按元素来删除的。 1、pop()默认删除列表中最后一个元素，而且会返回删除的元素。此时的时间复杂度为O（1） 下面的例子中，…...
【Java 进阶篇】Java Web 编写注册页面案例
当涉及到创建一个Java Web注册页面时，你将需要涵盖很多不同的主题，包括HTML、CSS、Java Servlet和数据库连接。在这篇文章中，我们将详细介绍每个步骤，以帮助你创建一个完整的注册页面。 1. 介绍 注册页面是许多Web应用程序的关键…...
7.5 SpringBoot 拦截器Interceptor实战 统一角色权限校验
前言 在【7.1】管理员图书录入和修改API，当时预告过：并没有写【校验是否是管理员】的逻辑，因为是通用逻辑，会单写一篇来细讲，那么今天就来安排！ 角色权限校验，是保证接口安全必备的能力：有权限才可以操作！所以，一般对于这种通用逻辑，推荐不与主业务逻辑耦合，那么…...
通过Wrangler CLI在worker中创建数据库和表
官方使用文档：Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后，会在本地和远程创建数据库： npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库： 现在，您的Cloudfla…...
python爬虫：Newspaper3k 的详细使用（好用的新闻网站文章抓取和解析的Python库）
更多内容请见： 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...
Caliper 配置文件解析：config.yaml
Caliper 是一个区块链性能基准测试工具，用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构，并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件，主要包含以下几个部…...
是否存在路径（FIFOBB算法）
题目描述 一个具有 n 个顶点e条边的无向图，该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序，确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数，分别表示n 和 e 的值（1…...
DeepSeek 技术赋能无人农场协同作业：用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言： 在Java编程中，类的生命周期是指类从被加载到内存中开始，到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期，让读者对此有深刻印象。 目录 …...
代码规范和架构【立芯理论一】（2025.06.08）
1、代码规范的目标 代码简洁精炼、美观，可持续性好高效率高复用，可移植性好高内聚，低耦合没有冗余规范性，代码有规可循，可以看出自己当时的思考过程特殊排版，特殊语法，特殊指令，必须…...
Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一：使用Read()读取文件2.3、方式二：bufio读取文件2.4、方式三：os.ReadFile读取2.5、写…...
作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作：验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化：测试aof和aof持久化机制，确保数据在开启后正确恢复。 事务：检查事务的原子性和回滚机制。 发布订阅：确保消息正确传递。 2、性…...