Practical Memory Leak Detection using Guarded Value-Flow Analysis 论文阅读
本文于 2007 年投稿于 ACM-SIGPLAN 会议1。
概述
指针在代码编写过程中可能出现以下两种问题:
-
存在一条执行路径,指针未成功释放(内存泄漏),如下面代码中注释部分所表明的:
int foo() {int *p = malloc(4 * sizeof(int));if (p == NULL)return -1;int *q = malloc(4 * sizeof(int));if (q == NULL)return -1; // 注意这里,q为NULL时p一定不为NULL,但是函数直接返回,导致p所指向的区域未释放// some code to executefree(p);free(q);return 0; } -
存在一条执行路径,指针被重复释放(未定义行为),如
free一个空指针。int *p = (int *)malloc(4 * sizeof(int));int *q = p;free(q);q = p;free(q);
最笨拙的方法是枚举每一条可能的路径,依次判断。但是这显然是不切实际的。因而本文的主要工作是提出一个能够发现未释放指针或重复释放指针的高效算法,并进行了代码实现,提示编写者具体可能的错误原因。即给定一个程序,找到其中可能存在的这种问题。
首先进行控制流图(Condition-Flow Graph,CFG)的约定:
- 赋值(运算节点): e = e ′ e=e' e=e′。
- 函数调用: e = f ( p 1 , p 2 , ⋯ , p m ) e=f(p_1,p_2,\cdots,p_m) e=f(p1,p2,⋯,pm)。
- 返回: return e \texttt{return}\ e return e。
- 分支节点: switch e ( c 1 , n 1 ; c 2 , n 2 ; ⋯ ; c k , n k ; n t ) \texttt{switch}_e(c_1,n_1;c_2,n_2;\cdots;c_k,n_k;n_t) switche(c1,n1;c2,n2;⋯;ck,nk;nt)。即一个节点根据表达式 e e e 的值不同可以有 k + 1 k+1 k+1 个分支跳转地址,分别记作 I n = { n 1 , n 2 , ⋯ , n k , n t } I_n=\{n_1,n_2,\cdots,n_k,n_t\} In={n1,n2,⋯,nk,nt},最后一个为默认跳转地址。
此外,本文将问题进行了规约:定义 s o u r c e − s i n k [ n , m ] {\rm source-sink}[n,m] source−sink[n,m] 问题为从 s r c \rm src src 会流入到 [ n , m ] [n,m] [n,m] 个 s i n k \rm sink sink 的条件可满足性问题。对于未释放,则是 s o u r c e − s i n k [ 0 , 0 ] {\rm source-sink}[0,0] source−sink[0,0] 问题,而多次释放则是 s o u r c e − s i n k [ 2 , ∞ ] {\rm source-sink}[2,\infty] source−sink[2,∞] 问题,而合法性判断是 s o u r c e − s i n k [ 1 , 1 ] {\rm source-sink}[1,1] source−sink[1,1] 问题。
算法流程
整体算法流程图如下所示:

- 利用编译器前端搭建 CFG。
- 到达定值点分析
- 值流图构建
- 无条件可达性分析,即不考虑具体控制流图上条件进行的分析
- 条件可达性分析,即考虑控制流图上条件进行的分析。
在实现该算法的同时还需要调用:
- 指针区域分析,即分析流图中每个指针所指向的内存区域。
- 条件分析。
- SAT(可满足性问题)解决器,即给定一组条件约束,返回一组可满足所有条件的初始值或报告无解。下文会将本论文中提出的问题规约到可满足性问题。
到达-定值分析(Reaching-Definition Analysis)
编译原理中经典的数据流分析方法。下文中用 p d o m ( x , n , m ) pdom(x,n,m) pdom(x,n,m) 来描述变量 x x x 能不能从 CFG 上流图节点 n n n 值不发生改变的到节点 m m m。论文中的 S S S 仅为一个记忆化的集合,不做具体参数使用。 p d o m pdom pdom 的计算使用逆向数据流分析方法:
p d o m ( x , n , m ) = { t r u e , m = n f a l s e , n 没有出边(返回节点) ⋀ i ∈ I n p d o m ( x , i , m ) ∧ ¬ d e f i n e ( x , i ) , 其他情况 pdom(x,n,m)= \begin{cases} true, m=n\\ false,\text{$n$ 没有出边(返回节点)}\\ \bigwedge_{i \in I_n} pdom(x,i,m) \wedge ^\lnot{define}(x,i),\text{其他情况} \end{cases} pdom(x,n,m)=⎩ ⎨ ⎧true,m=nfalse,n 没有出边(返回节点)⋀i∈Inpdom(x,i,m)∧¬define(x,i),其他情况
其中 d e f i n e ( x , i ) define(x,i) define(x,i) 表示 i i i 节点没有进行对变量 x x x 的赋值操作。
构建值流图(Value-Flow Graph)
在构建值流图之前首先需要介绍 free 函数的工作原理或特性。它释放传入参数给定的指针所指向的区域,也就是说它是针对内存区域而非指针的。例如下面的两个例子:
- 下面代码中
p1和p2指针所指向的区域都被释放了。
int *p1 = malloc(4 * sizeof(int)), *p2 = malloc(6 * sizeof(int));int *q = p1;free(q);q = p2;free(q);
- 下面代码中
p指针指向区域并未完全释放——p指针所指向的区域仍有一个int大小的空间未释放。
int *p = malloc(4 * sizeof(int));int *q = p + 1;free(q);
基于以上两个特性,构建如下的节点:
-
赋值(运算)节点。针对 CFG 上每个形如 x = y x=y x=y 形式的赋值语句都对应一个 VFG 的节点。
-
内存区域节点。由于
free是针对区域而非指针型变量,因而需要用一个单独的节点描述它是否有被释放的途径。该部分节点用 n r n_r nr 表示,可以使用这篇论文2中的方法快速描述代码中每个指针可能对应的内存区域集合。这里还需要注意的是,由于指针存在加减法操作,因而这里需要额外使用一个偏移量来去衡量该内存地址的具体使用情况。
-
释放节点。每个
free函数调用的节点都对应一个 VFG 上的汇(sink)点。 -
函数调用实参节点。由于进行函数调用,可以视为进行一次变量的值使用,记为 x @ n x_{@}n x@n。
-
函数调用形参节点。在被调用函数(callee)中该函数作为新变量使用,同时它对应于调用函数(caller)的一个变量。为避免函数多次调用导致边关系混乱,因而新建一个形参节点以解决图过于混乱的问题,记为 [ p ] [p] [p]。
-
函数返回节点。函数的返回值可能在 caller 中作为一个新变量继续存在,并涉及后续赋值和计算。
遍历 CFG,按如下规则建图(假设当前节点为 n n n):
- 赋值语句 y = x y=x y=x、释放节点 f r e e ( x ) free(x) free(x)、返回节点 r e t u r n ( x ) return(x) return(x):将所有 x x x 的定值点集合 n x n_x nx 建立一条边连到 n n n 节点。
- y = f ( x 1 , x 2 , ⋯ , x m ) y=f(x_1,x_2,\cdots,x_m) y=f(x1,x2,⋯,xm):对于每个函数实参 x i x_i xi,首先将 x i x_i xi 的定值点集合连接一条边到对应的实参节点( n x i → x i @ n n_{x_i} \to {x_i}_@n nxi→xi@n),然后每个实参节点连接到形参节点 x i @ n → p i {x_i}_{@}n \to p_i xi@n→pi,最后将 callee 函数的返回节点 n r e t f n_{\rm ret}^f nretf 连接到当前函数调用节点(该语句可以视为一种特殊类型的赋值语句) n r e t f → n n_{\rm ret}^f \to n nretf→n。
- 对于赋值变量中 x x x 或 y y y 不是一个有效节点的(如
malloc函数返回的堆区域指针),调用内存区域查询函数返回对应的内存区域节点。
无条件可达性分析(Unguarded Reachability Detection)
该步骤中忽略了程序流图中的条件,即认为所有的边都是可走到的,在这种情况下先简单分析是否每个 malloc 函数都有至少一个 free 与之对应。
- 枚举一个起始点 s r c src src,首先找到 VFG 顺向流图中可到达节点集合 F s r c F_{src} Fsrc
- 找到 F s r c F_{src} Fsrc 中所有的
free语句对应节点,记为 K K K。 - 分类讨论:
- 如果 K K K 为空,则该
malloc语句无对应free语句,直接报告内存泄漏。 - 如果从该 s r c src src 节点可以到达一个内存区域节点,则说明该代码片段中存在全局变量,暂时不继续分析该代码的内存泄漏问题,直接退出。
- 找到能从 s r c src src 到并且能到达 K K K 的集合 R R R,并将 R R R 集合传递到下一步继续分析。
- 如果 K K K 为空,则该
条件可达性分析(Guarded Reachability Detection)
预处理
首先在 CFG 上进行条件分析。考虑每个分支节点 n n n 需要满足其分支出口唯一,即对于分支节点 n n n: switch e ( c 1 , n 1 ; c 2 , n 2 ; c k , n k ; n t ) \texttt{switch}_e(c_1,n_1;c_2,n_2;c_k,n_k;n_t) switche(c1,n1;c2,n2;ck,nk;nt),需要满足:
C n = [ ⋁ i ( e = c i ) n ] ∧ [ ⋀ i ≠ j ( e = c i ) n ∧ ( e = c j ) n ‾ ] C_n=\left [\bigvee_{i}(e=c_i)_n\right] \wedge \left[\bigwedge_{i \ne j} \overline{(e=c_i)_n \wedge (e=c_j)_n}\right] Cn=[i⋁(e=ci)n]∧ i=j⋀(e=ci)n∧(e=cj)n
即存在一条出路,且不存在一个条件同时满足两条出路。
定义函数 c g ( x , n , m ) cg(x,n,m) cg(x,n,m)(下简写成 c g u a r d ( n → m ) cguard(n \to m) cguard(n→m),其中程序点 n n n 为形如 x = e x=e x=e 的赋值语句)表示变量 x x x 从程序点 n n n 到 m m m 需要满足的输入条件集合,有如下递推:
c g ( x , n , m , E ) = { t r u e , 如果满足支配关系即 p d o m ( x , n , m ) c g ( x , n 1 , m , E ) , n 处无分支, n 1 为 n 语句的唯一后续语句 ⋁ i ∈ I n , x , E c o n d ( n , n i , E ) ∧ c g ( x , n i , m , E ∪ { ⟨ n , n i ⟩ } ) , 其他情况 cg(x,n,m,E)= \begin{cases} true,\texttt{如果满足支配关系即 $pdom(x,n,m)$}\\ cg(x,n_1,m,E),\texttt{$n$ 处无分支,$n_1$ 为 $n$ 语句的唯一后续语句}\\ \bigvee_{i \in I_{n,x,E}} cond(n,n_i,E) \wedge cg(x,n_i,m,E \cup \{\langle n,n_i\rangle\}),\texttt{其他情况} \end{cases} cg(x,n,m,E)=⎩ ⎨ ⎧true,如果满足支配关系即 pdom(x,n,m)cg(x,n1,m,E),n 处无分支,n1 为 n 语句的唯一后续语句⋁i∈In,x,Econd(n,ni,E)∧cg(x,ni,m,E∪{⟨n,ni⟩}),其他情况
其中 I n , x , E I_{n,x,E} In,x,E 表示满足后续节点不是形如 d e f i n e ( n i , x ) define(n_i,x) define(ni,x) 且 ⟨ n , n i ⟩ \langle n,n_i \rangle ⟨n,ni⟩ 不在 E E E 中的后续节点集合 { n i } \{n_i\} {ni}。 c o n d ( n , n i , E ) cond(n,n_i,E) cond(n,ni,E) 函数表示从 n n n 节点走到 n i n_i ni 节点所需要满足的条件,并且要求 n n n 节点后续不能有 E E E 中的边:
c o n d ( n , n i , E ) = { ( e = c i ) n , n 是一个分支节点,且 n 的后续集合不在 E 集合中 t r u e , 其他情况 cond(n,n_i,E)= \begin{cases} (e=c_i)_n,\texttt{$n$ 是一个分支节点,且 $n$ 的后续集合不在 $E$ 集合中}\\ true,\texttt{其他情况}\\ \end{cases} cond(n,ni,E)={(e=ci)n,n 是一个分支节点,且 n 的后续集合不在 E 集合中true,其他情况
这里 ( e = c i ) n (e=c_i)_n (e=ci)n 表示在程序分支判断点 n n n 处进行条件判断 e = c i e=c_i e=ci。
这里加入 E E E 集合(已遍历的边集合)作为参数是方便代码实现上的,由于流图中可能有环存在,因而不能重复遍历同一条边,通过在状态中多维护一个 E E E 集合可以有效防止重复遍历到同一条边。在 c o n d cond cond 中,显然要进入循环然后退出该循环需要同时满足在循环的出口判断中 e = c i e=c_i e=ci 和 e ≠ c i e \ne c_i e=ci,这显然是永假的。因而这里加入了边的限制条件以防止上述情况的出现。当然这里会存在一个小漏洞就是仅判断了循环入口点的条件,未判断出口点的。这里会对未释放问题的判定产生一定的影响,但是对多重释放不会。
接下来就是考虑利用这些条件在 VFG 上进行条件判断。同样定义 v g u a r d ( n , m ) = v g ( n , m ) vguard(n,m)=vg(n,m) vguard(n,m)=vg(n,m) 函数表示从 VFG 图上 n n n 节点走到 m m m 的约束条件集合,有:
v g ( n , m , E ) = { t r u e , n = m ⋁ n → n ′ ∈ E c g u a r d ( n → n ′ ) ∪ v g ( n ′ , m , E ∪ { n → n ′ } ) , 其他情况 vg(n,m,E)= \begin{cases} true,n=m\\ \bigvee_{n \to n' \in E} cguard(n \to n') \cup vg(n',m,E \cup \{n \to n'\}),\texttt{其他情况} \end{cases} vg(n,m,E)={true,n=m⋁n→n′∈Ecguard(n→n′)∪vg(n′,m,E∪{n→n′}),其他情况
和在 CFG 上的情况类似,这里只需要在 VFG 图上再加入 CFG 上的信息即可。
分析过程
考虑对于一个确定的 s r c src src 节点和所有该指针的释放操作汇点 K K K,在 2.3 节中阐述的 R R R 集合上进行分析。定义 G k = v g u a r d ( s r c , k ) G_k=vguard(src,k) Gk=vguard(src,k), C C C 为 R R R 上所有的分支节点需要满足的 C n C_n Cn 的与集合。此时就满足了一个 SAT 问题的框架:
- 如果此处存在一组初值指派满足 ∨ k ∈ K G k ‾ ∧ C \overline{\vee_{k \in K} {G_k}} \wedge C ∨k∈KGk∧C,则表明存在某种初值指派,使得从该 s r c src src 语句无法走到任何一个汇点,即发生了内存泄漏。
- 如果存在一组初值指派,满足 ∃ i ≠ j , G i ∧ G j ∧ C \exists i \ne j,G_i \wedge G_j \wedge C ∃i=j,Gi∧Gj∧C,则表明某组初值指派可以到达两个不同的
free语句,进行多次释放操作,因而发生未定义行为(Undefined Behavior)。
可以注意到上述的操作时间复杂度是比较高的,特别是对于有大量 malloc 语句存在的时候。因而本文中仅对操作数不超过阈值 30 30 30 的代码进行分析。
本文同时实现了代码,将所有的错误种类分成以下几类:
- 从未释放。又分为:a)指针作为局部变量在 main 函数或其他函数未释放;b)指针作为全局变量或存在于数组等结构中未释放。
- 释放。又分为:a)一切条件下都能释放;b)某些情况下能释放,有些情况未释放。
- 不能判定,认为释放了。这种情况通常因为分析语句过多导致超过阈值停止分析。
Cherem S, Princehouse L, Rugina R. Practical memory leak detection using guarded value-flow analysis[C]//Proceedings of the 28th ACM SIGPLAN Conference on Programming Language Design and Implementation. 2007: 480-491. ↩︎
Bjarne Steensgaard. Points-to analysis in almost linear time. In Proceedings of the ACM Symposium on the Principles of Programming Languages, St. Petersburg Beach, FL, January 1996. ↩︎
相关文章:

Practical Memory Leak Detection using Guarded Value-Flow Analysis 论文阅读
本文于 2007 年投稿于 ACM-SIGPLAN 会议1。 概述 指针在代码编写过程中可能出现以下两种问题: 存在一条执行路径,指针未成功释放(内存泄漏),如下面代码中注释部分所表明的: int foo() {int *p malloc(4 …...
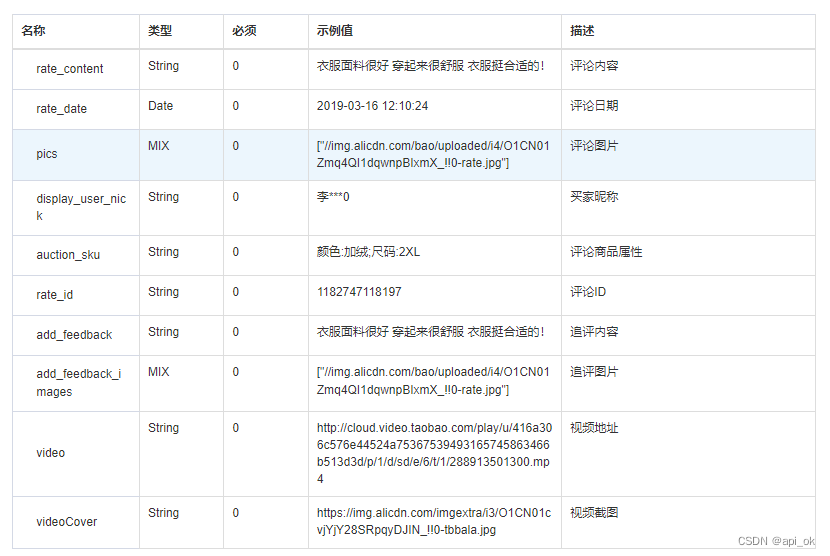
淘宝天猫商品历史价格API接口
获取淘宝商品历史价格接口的步骤如下: 注册淘宝开放平台:首先在淘宝开放平台上注册一个账号,并进行登录。创建应用:在淘宝开放平台上创建一个应用,并获取该应用的App Key和App Secret,用于后续的接口调用。…...

从0开始学go第七天
gin获取表单from中的数据 模拟简单登录页面: <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><title>login</title> </head><body><form action"/login" method&q…...

【牛客面试必刷TOP101】Day7.BM31 对称的二叉树和BM32 合并二叉树
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:牛客面试必刷TOP101 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!&…...
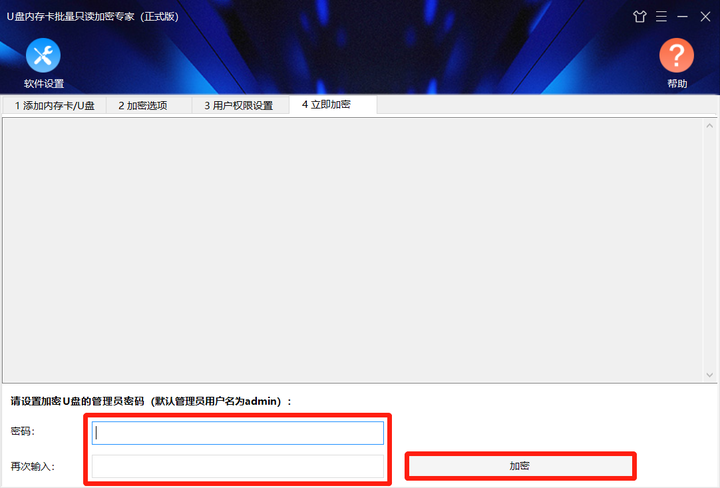
U盘怎么设置为只读?U盘怎么只读加密?
当将U盘设置为只读模式时,将只能查看其中数据,无法对其中数据进行编辑、复制、删除等操作。那么,怎么将U盘设置成只读呢? U盘如何设置成只读? 有些U盘带有写保护开关,当打开时,U盘就会处于只读…...

为什么MyBatis是Java数据库持久层的明智选择
在Java应用程序的开发中,选择合适的数据库持久层框架至关重要。一个明智的选择可以帮助开发人员更好地管理数据库交互、提高性能和简化开发工作。 (一)为什么要选MyBatis JDBCHibernate / JPAMyBatis简单直接ORM轻量动态SQL关联查询开发效率…...
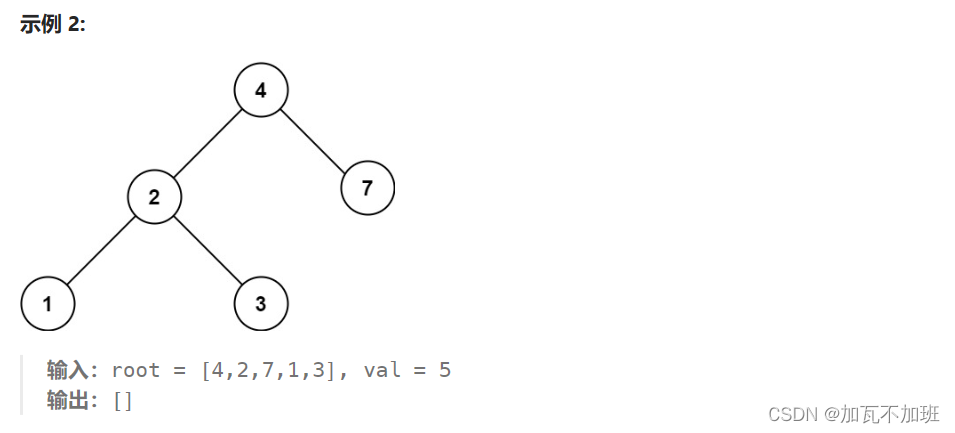
二叉搜索树--查询节点-力扣 700 题
例题细节讲过(二叉搜索树的基础操作-CSDN博客),下面给出递归实现 public TreeNode searchBST(TreeNode node, int val) {if(node null) {return null;}if(val < node.val) {return searchBST(node.left, val);} else if(node.val < val) {return searchBST(…...
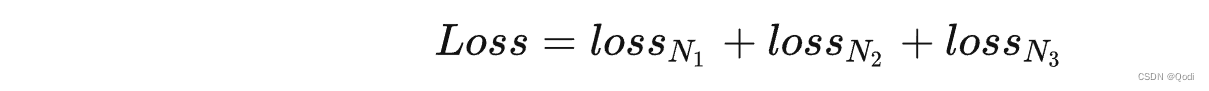
YOLOv3 | 核心主干网络,特征图解码,多类损失函数详解
https://zhuanlan.zhihu.com/p/76802514) 文章目录 1. 核心改进1.1主干网络1.2 特征图解码1.2.1 检测框(位置,宽高)解码1.2.2 检测置信度解码1.2.3 类别解码 1.3 训练损失函数1.3.1 正负样本定义1.3.2 损失函数 1. 核心改进 1.1主干网络 更…...

Java架构师API设计
目录 1 导学2 架构师的角度来审视API2.1 API狭隘理解2.2 API广义理解2.3 API的用途不同定义2.4 面向抽象编程的Java开发2.5 API在提高系统的可维护性和可扩展性方面的作用3 架构师必备的API设计原则3.1 标准化原则3.2 易用性原则3.3 扩展性原则3.4 兼容性原则3.5 抽象性原则3.6…...

.net也能写内存挂
最近在研究.net的内存挂。 写了很久的c,发现c#写出来的东西实在太香。 折腾c#外挂已经有很长时间了。都是用socket和c配合。 这个模式其实蛮成功的,用rpc调用的方式加上c#的天生await 非常好写逻辑 类似这样 最近想换个口味。注入托管dll到非托管进程 这样做只…...

python学习笔记2-数字转化为String
题目链接 str() 强制转换, sorted() 转换为有序列表,join() 将列表中的元素连接到字符串中,然后奇偶位组合成数字 class Solution:def splitNum(self, num: int) -> int:stnum "".join(sorted(str(num)))num1, num2 int(stn…...
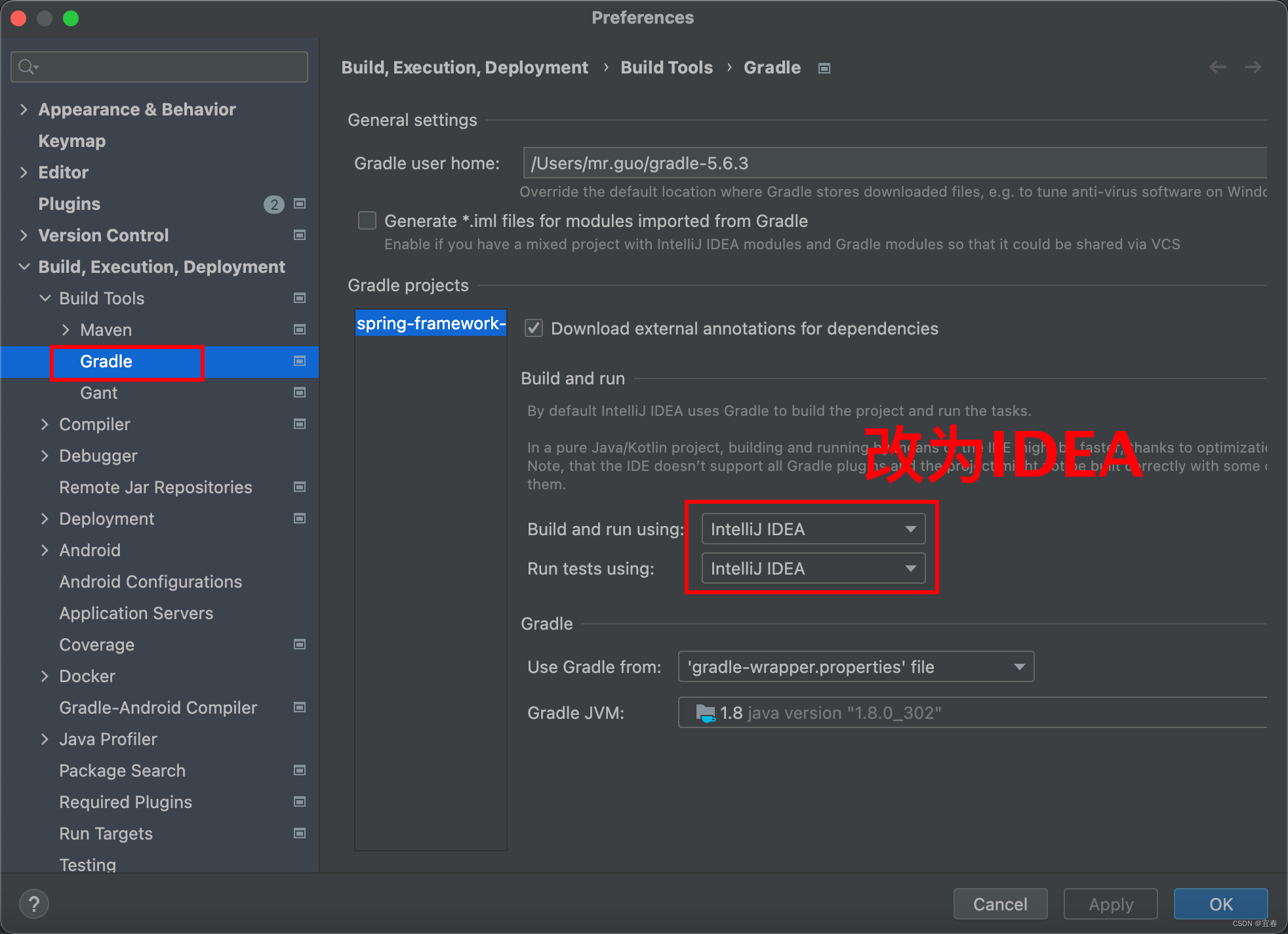
MAC版Gradle构建Spring5.X源码阅读环境
前言: 三年前鄙人有幸在现已几乎报废的Window的DELL中搭建过Spring源码环境,今天,Mac版的搭建,来了。 本篇文章环境搭建:Spring5.2.1 Gradle5.6.3-all jdk8 IDEA2022.3版本 文章目录 1、Spring源码下载2、Gradle下载…...

Linux 常用通配符
通配符是一种特殊语句,主要有星号(*)和问号(?),用来模糊搜索文件。当查找文件夹时,可以使用它来代替一个或多个真正字符;当不知道真正字符或者懒得输入完整名字时&#x…...

Python皮卡丘
系列文章 序号文章目录直达链接1浪漫520表白代码https://want595.blog.csdn.net/article/details/1306668812满屏表白代码https://want595.blog.csdn.net/article/details/1297945183跳动的爱心https://want595.blog.csdn.net/article/details/1295031234漂浮爱心https://want…...

【数据结构与算法】三种简单排序算法,包括冒泡排序、选择排序、插入排序算法
冒泡排序算法 冒泡排序他是通过双重循环对每一个值进行比较,将小的值向后移动,以达到最终排序的结果,他的时间复杂度为O(n^2)。 /*** 冒泡排序* param arr*/public static void bubbleSort(int[] arr){int l arr.length;for (int i 0; i <…...
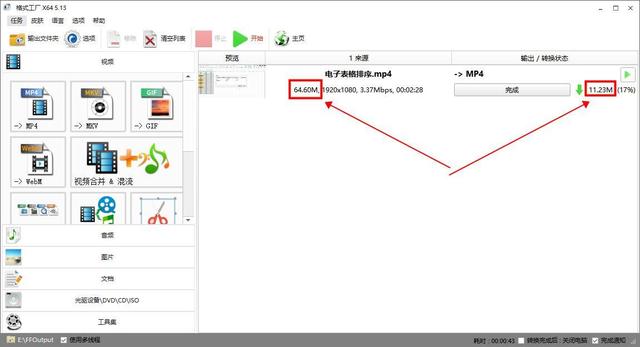
视频太大怎么压缩变小?超过1G的视频这样压缩
视频已经成为了我们日常生活中不可或缺的一部分,然而,很多时候,我们可能会遇到视频文件过大,无法在某些平台上传或保存的问题。那么,如何将过大的视频文件压缩变小呢? 下面就给大家分享三款实用的工具&…...
Edge 无法登录/同步问题【一招搞定】
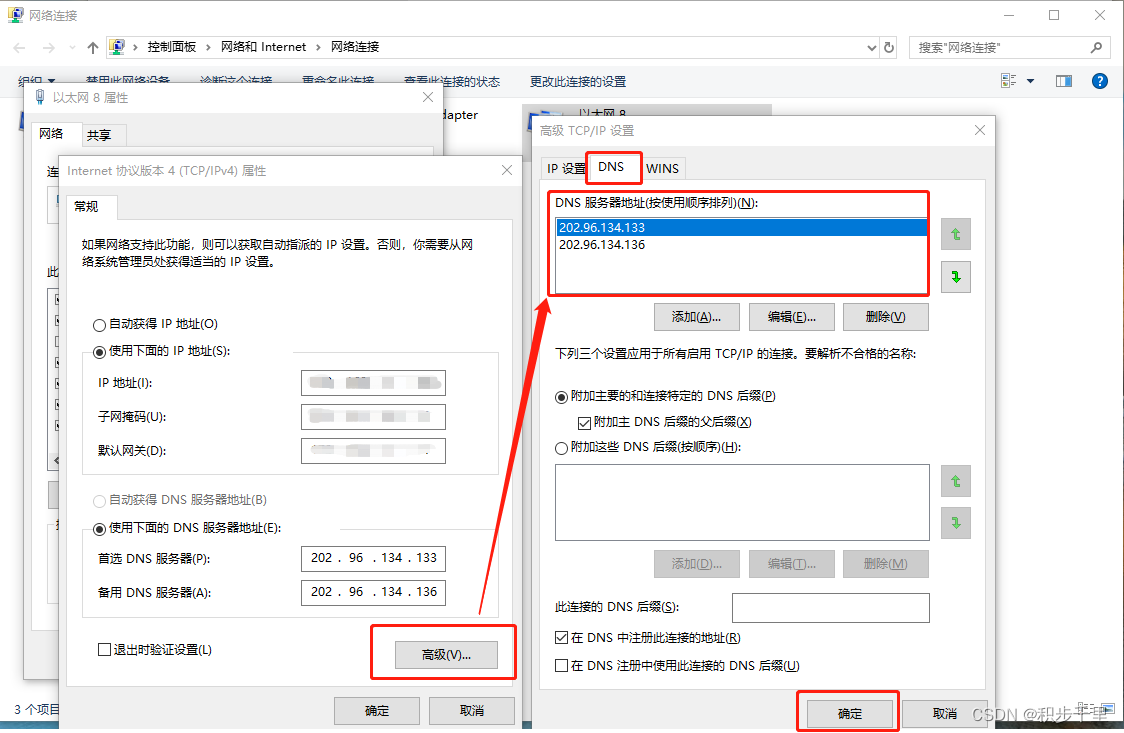
目录 前言 一、打开 Edge 浏览器显示未同步,点击同步无效 二、Edge 登录报错 0x801901f4 或 0x80190001 解决方法 2.1 报错 0x801901f4 解决方法 2.1.0 Edge 登陆报错图示 2.1.1 添加 Edge 推荐的 DNS 地址 2.1.2 重新登录 Edge 账号成功 2.2 报错 0x801…...
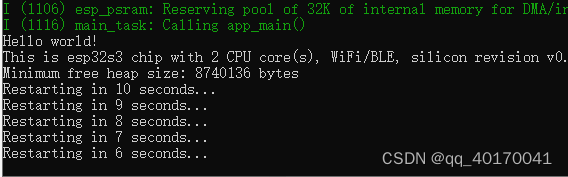
ESP32-S3上手开发
1、搭建开发环境 首先搭建开发环境,这里采用了windows下集成开发环境ide进行开发,具体的安装方法:ESP-IDF安装配置 这里使用的乐鑫的esp32s3,N16R8 2、esp32s3模块 从上面图中可以看到,N16R8这里使用了外扩16M的fl…...

UE4和C++ 开发-编程基础记录(UE4+代码基础知识)
1、UE4基础元素 ①Actor 我们又见面了Actor,Actor是在一个关卡中持续存在的,通常他包含几个Actor组件。支持网络复制和多人游戏。 Actor不包含位置,方向。这些东西在Root Component中存储。对于UE3 中的Pawn也由PlayerCharacter继承了…...
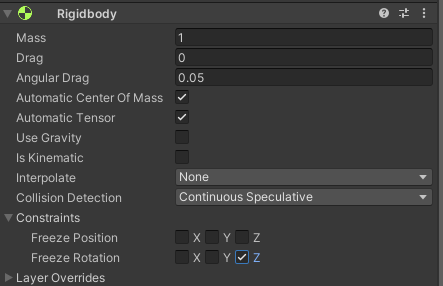
【Unity】【VR】如何让Distance Grab抓取物品时限制物品的Rotation
【背景】 遇到这样的场景,希望抓取Canvas时,Canvas不会沿Z轴旋转。 【问题】 发现Freeze Canvas的Rigid Body没有用。 【分析】 应该是RigidBody的限制仅在物理互动下生效,抓取可能不属于物理互动(比如碰撞),所以不生效。 【思路】 还是得写脚本挂载在Interacta…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
