[NOIP 2022] 建造军营 题解
题目
P1 边双缩点
观察样例二,可以发现边双内的边可选可不选。由此考虑边双缩点,Tarjan 找桥即可,缩点后变成一棵树。
P2 设计状态
用最终合法答案形态截这颗树,设计 f u f_u fu 表示 u u u 子树内非空,且子树内军营到 u u u 的边均被保护的方案数。
P3 转移
为方便转移,记 g u g_u gu 表示 u u u 子树空的方案数,遍历 u u u 的儿子 v v v:
- v v v 不选,则 v v v 之前非空, f u × 2 × g v f_u \times 2\times g_v fu×2×gv。
- v v v 选, ( f u + g u ) × f v (f_u+g_u) \times f_v (fu+gu)×fv。
g u = ∏ ( 2 × g v ) g_u = \prod(2 \times g_v) gu=∏(2×gv)。
记 u u u 所在边双点数为 V u V_u Vu,边数为 E u E_u Eu。初值: f u = 2 V u + E u − 2 E u , g u = 2 E u f_u=2^{V_u+E_u}-2^{E_u},g_u=2^{E_u} fu=2Vu+Eu−2Eu,gu=2Eu。
P4 统计答案
假定只选 i i i 子树内的点,此时子树外的边均可选可不选。然而这样在 i i i 祖先处统计会重复计算 i i i 的贡献,强制不选 i → f a i i \to fa_i i→fai 这条边即可,其余子树外的边任意。
P5
#include <iostream>
#include <vector>
#define int long longusing namespace std;const int N = 5e5 + 5;
const int M = 1e6 + 5;
const int mod = 1e9 + 7;int n, m, pw[N + M];struct Edge{int to, nxt;
}e1[M << 1], e2[M << 1];int tot1 = 1, head1[N];
void add1(int u, int v)
{e1[++tot1] = {v, head1[u]}; head1[u] = tot1;
}int tot2 = 1, head2[N];
void add2(int u, int v)
{e2[++tot2] = {v, head2[u]}; head2[u] = tot2;
}int low[N], dfn[N], idx;
bool bridge[M << 1];
void Tarjan(int u, int from)
{low[u] = dfn[u] = ++idx;for(int i=head1[u]; i; i=e1[i].nxt){if((i ^ 1) == from) continue;int v = e1[i].to;if(!dfn[v]) // tree edge{Tarjan(v, i);low[u] = min(low[u], low[v]);if(low[v] >= dfn[v])bridge[i] = bridge[i ^ 1] = 1;}else low[u] = min(low[u], dfn[v]); // back edge}
}int cnt, belong[N], V[N], E[N];
void dfs0(int u)
{belong[u] = cnt, V[cnt] ++ ;for(int i = head1[u]; i; i = e1[i].nxt){int v = e1[i].to;if(belong[v] or bridge[i]) continue;dfs0(v);}
}int ans, siz[N], f[N], g[N];
void dfs(int u, int from)
{f[u] = pw[E[u]] * (pw[V[u]] - 1) % mod,g[u] = pw[E[u]], siz[u] = E[u];for(int i = head2[u]; i; i=e2[i].nxt){if((i ^ 1) == from) continue;int v = e2[i].to;dfs(v, i);siz[u] += siz[v] + 1;f[u] = f[u] * 2 * g[v] % mod + (f[u] + g[u]) * f[v] % mod; f[u] %= mod;g[u] *= 2 * g[v]; g[u] %= mod;}if(u == 1) ans += f[u], ans %= mod;else ans += f[u] * pw[m - siz[u] - 1] % mod, ans %= mod;
}signed main()
{cin >> n >> m;pw[0] = 1; for(int i=1; i<=m; i++) pw[i] = (pw[i-1] << 1) % mod;for(int i=1; i<=m; i++){int u, v;cin >> u >> v;add1(u, v); add1(v, u);}Tarjan(1, 0);for(int i=1; i<=n; i++){if(!belong[i]) ++ cnt, dfs0(i);}for(int i=2; i<=tot1; i++){int u = e1[i].to, v = e1[i ^ 1].to;if(belong[u] == belong[v]) E[belong[u]] ++ ;else add2(belong[u], belong[v]);}for(int i=1; i<=cnt; i++) E[i] >>= 1;dfs(1, 0);cout << ans;
}
相关文章:

[NOIP 2022] 建造军营 题解
题目 P1 边双缩点 观察样例二,可以发现边双内的边可选可不选。由此考虑边双缩点,Tarjan 找桥即可,缩点后变成一棵树。 P2 设计状态 用最终合法答案形态截这颗树,设计 f u f_u fu 表示 u u u 子树内非空,且子树…...
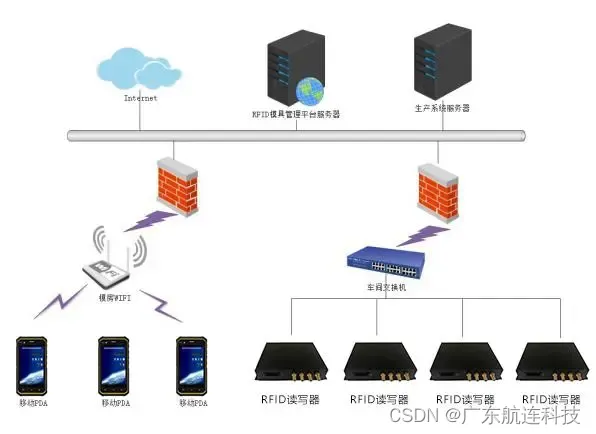
射频识别技术(RFID)在智能制造模具管理中的应用
背景介绍 模具是工业生产的核心装备,被誉为“工业之母”,广泛应用于机械、汽车、轻工、电子、化工、冶金、建材等各个行业,是制造加工企业的重要资产,然而,传统的人工纸质记录方式已无法满足模具管理的需求࿰…...
奖品定制经营商城小程序的作用是什么
奖品是激励人员团体很好的方式,也是荣誉象征,奖牌、奖杯、高端礼盒等,同时市场中团体非常多,其需求也是很多,尤其定制方面,就更是不用说。 对奖品定制企业来说,除了线下门店获客经营外…...

深度学习常用脚本总结
👨💻个人简介: 深度学习图像领域工作者 🎉工作总结链接:https://blog.csdn.net/qq_28949847/article/details/128552785 链接中主要是个人工作的总结,每个链接都是一些常用demo,…...
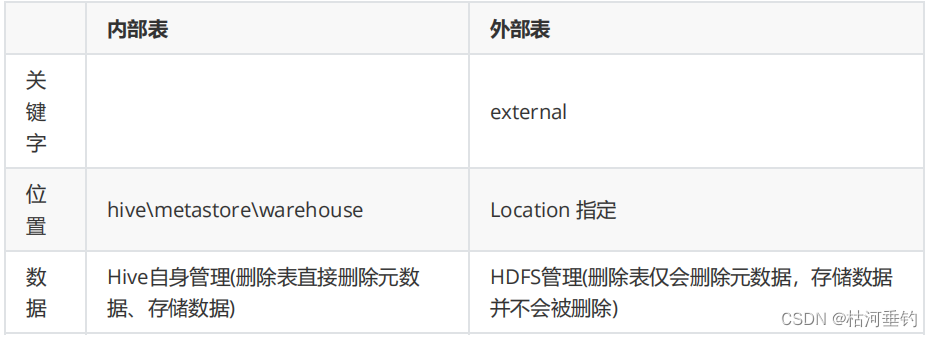
hive数据表创建
目录 分隔符 分区表 二级分区 分桶表 外部表 分隔符 CREATE TABLE emp( userid bigint, emp_name array<string>, emp_date map<string,date>, other_info struct<deptname:string, gender:string>) ROW FORMAT DELIMITED FIELDS TERMINATED BY \t COL…...
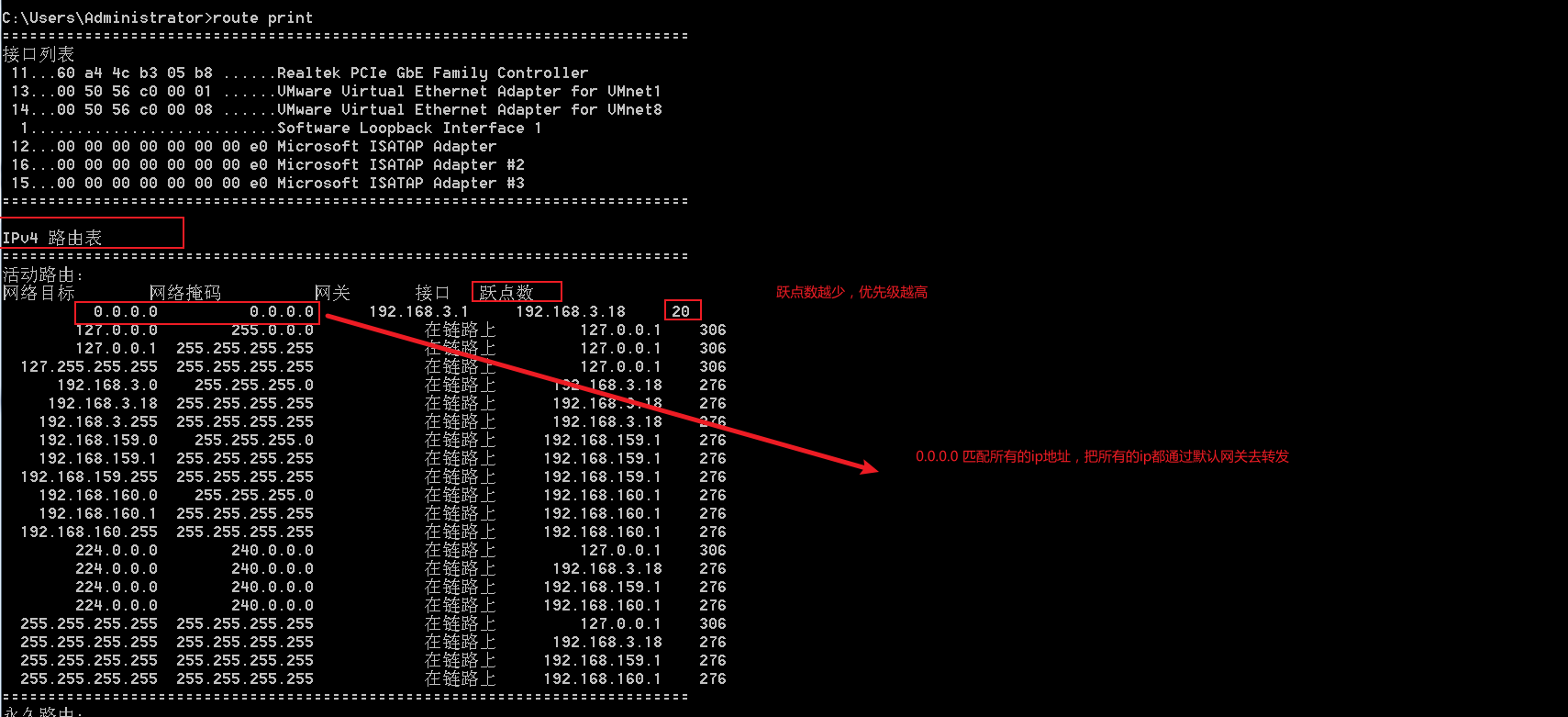
查看本机Arp缓存,以及清除arp缓存
查看Arp缓存目录 Windows 系统使用 winR,输入cmd 在命令窗口输入 arp -a 删除Arp缓存目录 在命令窗口输入 arp -d * 查看主机路由表...
Unity MRTK Hololens2眼动交互
/** ** UnityVersion : 2021.3.6f1* Description : 眼部交互基类* Author: * CreateTime : 2023-10-11 09:43:20* Version : V1.0.0* * */using System.Collections.Generic; using Microsoft.MixedReality.Toolkit.Input; using UnityEngine;namespace MRTKExtend.EyeTrackin…...
接口自动化测试 —— 协议、请求流程
一、架构 CRM客户关系管理系统 SAAS Software As A Service 软件即服务 PAAS Platform AS A Service 平台即服务 快速交付→ 快:自己去干、有结果、事事有回音、持续改进 单体架构——》垂直架构——》面向服务架构——》微服务架构(分布式…...

JDK安装详细教程
JDK安装详细教程 国内大多数使用的是1.8的版本,对于初学者来说这个版本很友善,不过由于我安装过了1.8,所以我这里演示JDK21 的安装,过程并无区别,只在下载时注意选择1.8版本。1.8就是JDK8. 文章目录 JDK安装详细教程一…...
vulnhub_Fowsniff靶机渗透测试
Fowsniff靶机 靶机地址:https://www.vulnhub.com/entry/fowsniff-1,262/ 文章目录 Fowsniff靶机信息收集web渗透密码碰撞POP3邮件服务器渗透获取权限权限提升靶机总结 信息收集 通过nmap扫描,靶机开放22 80 110 143端口,110是pop3邮件服务…...

FPGA面试题(3)
一.FPGA和CPLD区别 FPGA:现场可编程门阵列CPLD:复杂可编程逻辑器件 二.多位异步信号如何同步 单比特异步信号 慢时钟域->快时钟域:同步打拍快时钟域->慢时钟域:先拓展位宽再同步打拍 多比特异步信号 1.异步FIFO2.保持…...
Avalonia常用小控件Menu
1.项目下载地址:https://gitee.com/confusedkitten/avalonia-demo 2.UI库Semi.Avalonia,项目地址 https://github.com/irihitech/Semi.Avalonia 样式预览: axaml代码 : <UserControl xmlns"https://github.com/avalo…...

steam游戏服务器如何选择
steam游戏平台现在在国内市场很吃香,当我们自己开发的游戏想要上架steam我们需要准备什么,在选择服务器的时候我们又需要考虑哪些因素呢,该怎样选择一款适合自己游戏的服务器是很关键的。 Steam专用服务器通常是指由游戏开发商提供的服务器&…...
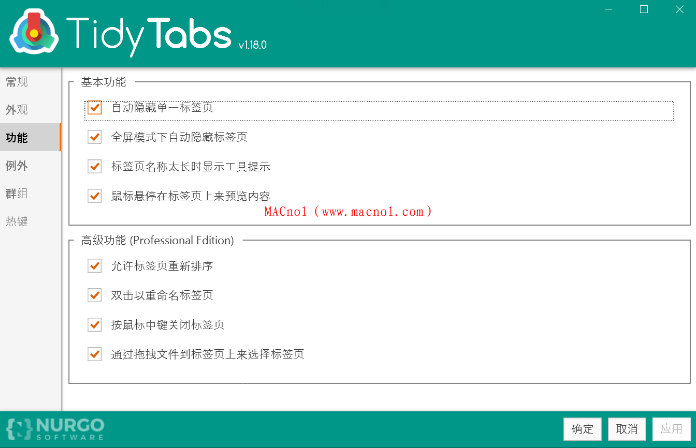
电脑技巧:推荐一款桌面整理神器TidyTabs
目录 1、软件简介 2、软件功能介绍 3、总结 1、软件简介 TidyTabs是一款Windows应用程序,它可以将多个打开的窗口整理成一个选项卡式的界面,使得用户可以更加方便地切换和管理不同的窗口。 TidyTabs可以将多个窗口整合到一个主窗口中,类似…...
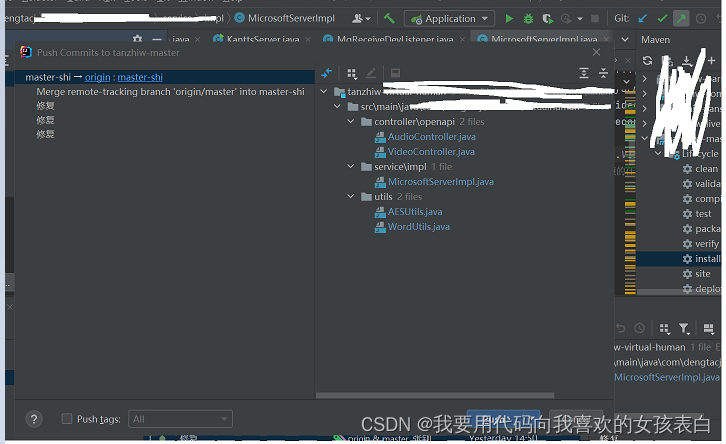
git合并分支-IDEA
有1个主分支,我从主分支拉取过来了,数据然后改好了,现在想合并到主分支上,并且将主分支的内容更新到我的分支下。用git怎么操作? 1.将主分支(master)的内容合并到我的分支(master-shi)中 在我的分支下执行 git merge master ID…...

winscope使用方法
Ubuntu下Android T的winscope工具使用方法 1. 在Android的项目源码中,prebuilts/misc/common/winscope目录下 直接使用chrome浏览器打开文件winscope.html 2. 可能会提示adb问题 进入目录development/tools/winscope/adb_proxy,有文件winscope_proxy.…...
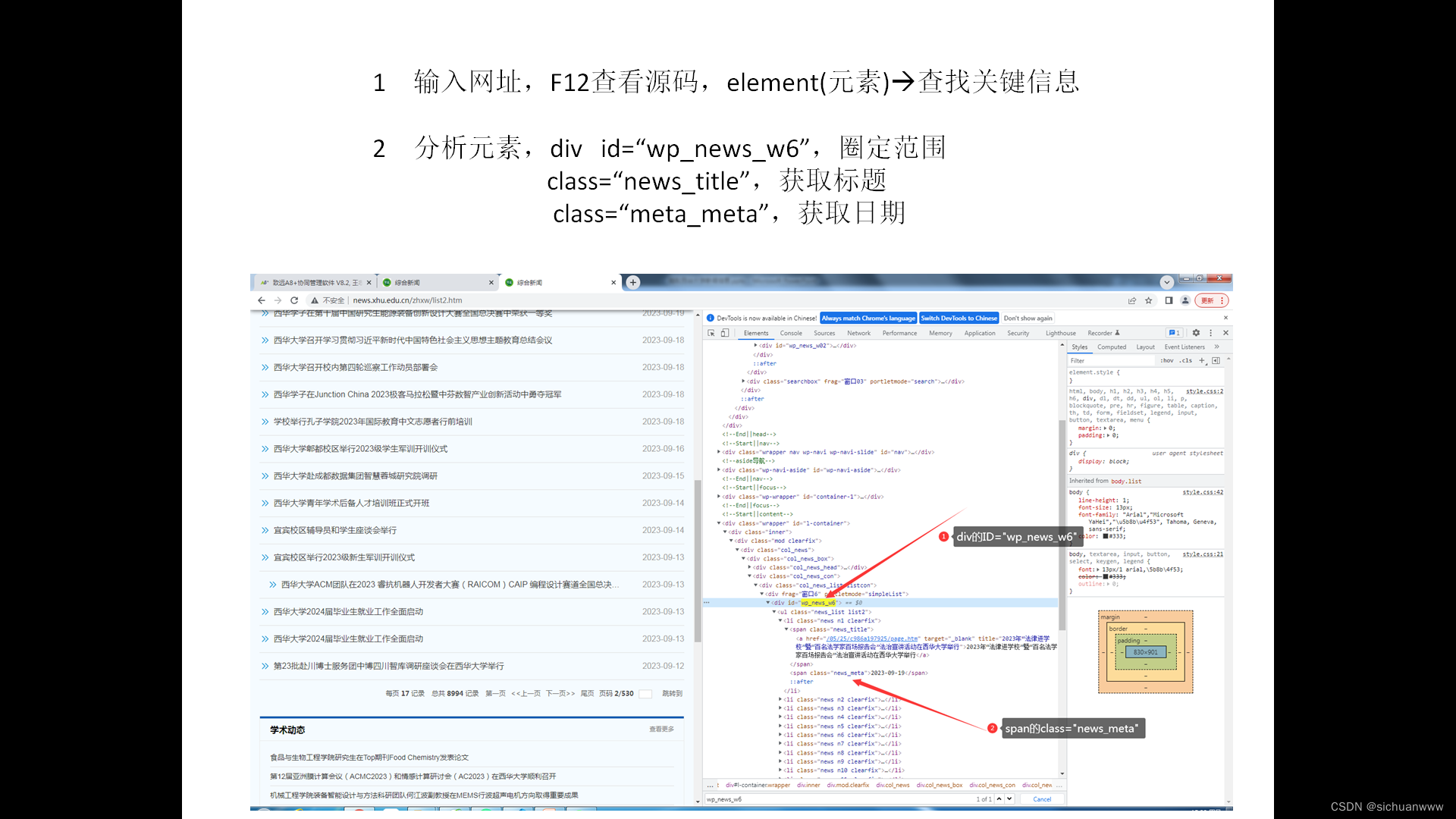
获取西华大学新闻网站信息(爬虫样例)
利用python的爬虫功能进行信息爬取,关键在于源码分析,代码相对简单。 1 源代码分析 访问网站,按下F12,进行元素查找分析。 2 代码实现 from requests import get from bs4 import BeautifulSoupdef getXhuNews(pageNum1):&qu…...

【Linux】https协议
文章目录 📖 前言1. 引入https协议2. 常见的加密方式2.1 对称加密:2.2 非对称加密:2.3 数据摘要&&数据指纹: 3. 对加密方式的探究3.1 只使用对称加密:3.2 只使用非对称加密:3.3 双方都使用非对称加…...

基于工业5G网关的工业机器人监测控制方案
随着智能制造、自动化生产的发展进步,工业机器人的身影越来越多地出现在工厂现场,成为新型无人化、智能化生产制造的中坚力量。 工业机器人的运行伴生着海量的数据采集、传输、分析和反馈执行,因此也需要高速、低延迟的5G网络,支撑…...

[Machine learning][Part4] 线性回归模型技巧
目录 正规方程法 梯度下降法 缩放特征 学习率选择 正规方程法 这种方法可以不多次迭代梯度下降函数就能得到w,b。但是缺点是在大量数据训练情况下效率较低,其次是这种算法仅仅在线性回归中实现了,并没有在其他模型中实现,因此,…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
