量子力学(4) 全同粒子
如果势能与时间无关,那么Ψ=ψe−iEt/ℏ\Psi=\psi e^{-iEt/\hbar}Ψ=ψe−iEt/ℏ,EEE是系统的总能量。
全同粒子分为玻色子和费米子。所有电子是全同的费米子。所有质子是全同的费米子。全同就是说不可能区分出其中的一个,比如说你摇了五个骰子,在掀开盖子之前我们好像没必要区分出其中的一个骰子(这是好例子还是坏例子?)。
两个全同的费米子不能有相同的波函数,这是泡利不相容原则。
如果两个粒子全同,那么哈密顿算符对于他们是一样的,就是说质量相等,并且V(r1,r2)=V(r2,r1)V(\bm{r_1},\bm{r_2})=V(\bm{r_2},\bm{r_1})V(r1,r2)=V(r2,r1)。PPP是交换算符,它的本征值是±1\pm 1±1。然后PPP和HHH对易。这很重要。我们知道HHH的本征函数就是薛定谔方程的解了。那么它们也要是PPP的本征函数,就是说ψ(r1,r2)=±ψ(r2,r1)\psi(\bm{r_1},\bm{r_2})=\pm\psi (\bm{r_2},\bm{r_1})ψ(r1,r2)=±ψ(r2,r1)。这里,玻色子取正号,费米子取负号。这是一般情况;可以分开的情况是特殊的(可以看见特殊满足一般)。
对于电子,总的波函数还要乘上自旋,即ψχ\psi\chiψχ。如果我们希望这个一共是反对称的,而如果要ψ\psiψ是对称的,就必须χ\chiχ是反对称的,所以现实里1,1合成中选择0,0合成态。
20:40
可以找到不对称也不反对称的薛定谔方程的解。如果要构造属于全同粒子的解,可以构造。
自旋波函数和位置波函数必须一个对称一个反对称。
角动量的合成也和自旋角动量一样,范围是差的绝对值到和。
正氦因为自旋波函数是对称的,所以位置波函数是反对称的,所以电子之间离得远,排斥势能低。Parahelium反之。
相关文章:
 全同粒子)
量子力学(4) 全同粒子
如果势能与时间无关,那么Ψψe−iEt/ℏ\Psi\psi e^{-iEt/\hbar}Ψψe−iEt/ℏ,EEE是系统的总能量。 全同粒子分为玻色子和费米子。所有电子是全同的费米子。所有质子是全同的费米子。全同就是说不可能区分出其中的一个,比如说你摇了五个骰子…...
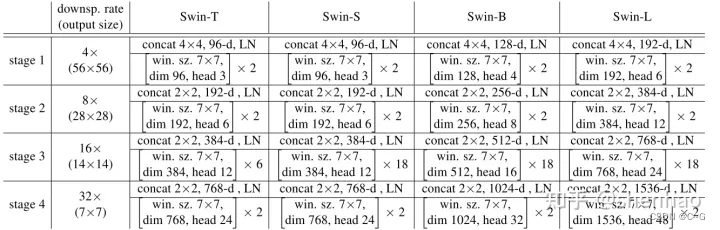
13、Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
简介 主页:https://github. com/microsoft/Swin-Transformer. Swin Transformer 是 2021 ICCV最佳论文,屠榜了各大CV任务,性能优于DeiT、ViT和EfficientNet等主干网络,已经替代经典的CNN架构,成为了计算机视觉领域通用…...

C++基础入门丨8. 结构体——还需要知道这些
Author:AXYZdong 硕士在读 工科男 有一点思考,有一点想法,有一点理性! 定个小小目标,努力成为习惯!在最美的年华遇见更好的自己! CSDNAXYZdong,CSDN首发,AXYZdong原创 唯…...
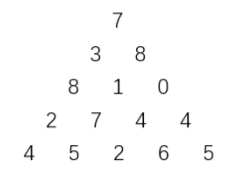
算法第十六期——动态规划(DP)之线性DP
【概述】 线性动态规划,是较常见的一类动态规划问题,其是在线性结构上进行状态转移,这类问题不像背包问题、区间DP等有固定的模板。 线性动态规划的目标函数为特定变量的线性函数,约束是这些变量的线性不等式或等式,目…...
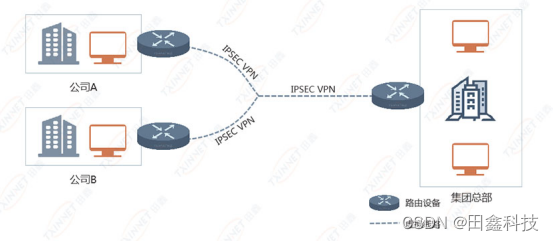
智慧新零售网络解决方案,助力新零售企业数智化转型
随着数字化时代的不断发展,新零售连锁业务模式“线上线下”融合发展,数据、设备在逐渐增加,门店数量也会随着企业规模的扩大而增加,但由于传统网络架构不稳定、延时、容量小影响服务质量(QoS)、分支设备数量…...

Go语言规范中的可赋值
了解可赋值规范的重要性当使用type关键字定义类型的时候,会遇到一些问题,如下:func main(){var i int 2pushInt(i) } type MyInt int //基于int定义MyInt func pushInt(i MyInt){}结果:调用函数pushInt报错 cannot use i (variab…...

外盘国际期货招商:原油市场热点话题
原油市场热点话题 问:目前美国原油库存如何? 答:EIA原油库存数据显示,由于美国炼油厂季节性检修,开工率继续下降,原油库存连续九周增长至2021年5月份以来最高水平,同期美国汽油库存减少而精炼…...
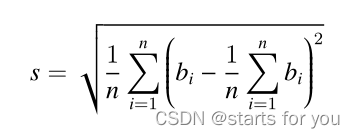
[蓝桥杯 2018 省 A] 付账问题 贪心题
几个人一起出去吃饭是常有的事。但在结帐的时候,常常会出现一些争执。现在有 n 个人出去吃饭,他们总共消费了 S 元。其中第 i 个人带了 ai 元。幸运的是,所有人带的钱的总数是足够付账的,但现在问题来了:每个人分别要出…...
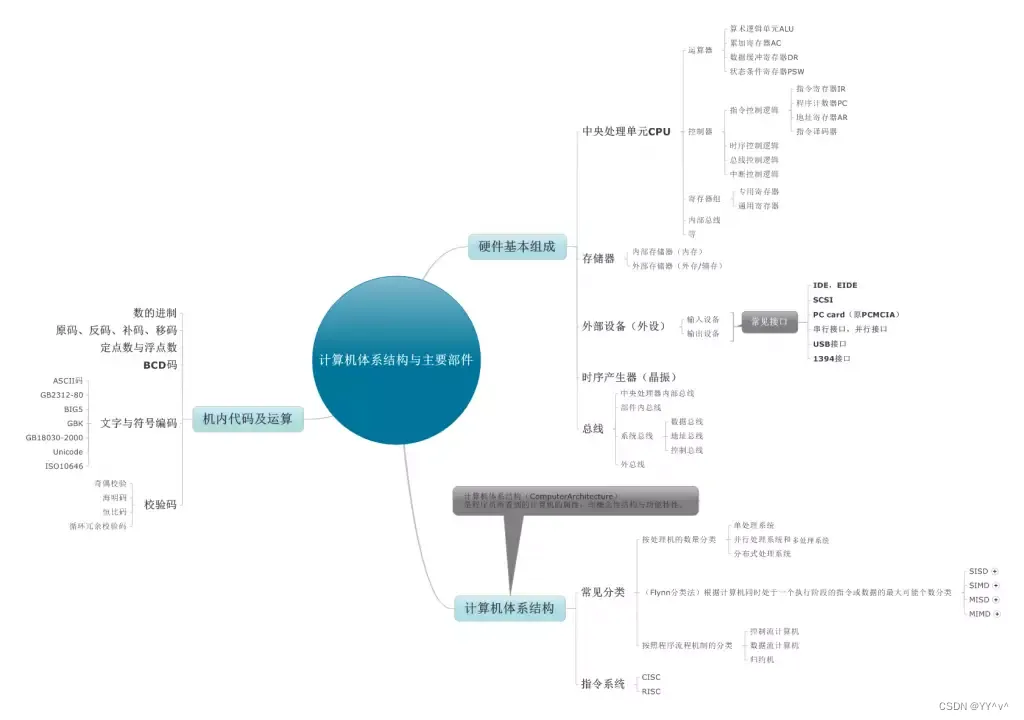
微机原理复习(周五),计算机组成原理图
1.计算机由运算器,控制器,存储器,输入设备,输出设备等5大基本部件组成。 2.冯诺依曼提出存储设计思想是:数字计算机的数制采用二进制,存储程序,程序控制。 3.计算机的基本组成框图:…...

用了10年Postman,意想不到它的Mock功能也如此强大
最近在做一些app,前后端分离的开发模式是必须的。一直用的python flask做后端的快速POC,python本身就是一门胶水语言,开发起来方便快捷,而flask又是一个极简的webserver框架(比Django简洁)。但在这里推荐的…...

项目重构,从零开始搭建一套新的后台管理系统
背景 应公司发展需求,我决定重构公司的后台管理系统,从提出需求建议到现在的实施,期间花了将近半个月的时间,决定把这些都记录下来。 之前的后台管理系统实在是为了实现功能而实现的,没有考虑到后期的扩展性…...

day20_Map
今日内容 上课同步视频:CuteN饕餮的个人空间_哔哩哔哩_bilibili 同步笔记沐沐霸的博客_CSDN博客-Java2301 零、 复习昨日 一、作业 二、比较器排序 三、Collections 四、Map 五、HashMap 六、TreeMap 零、 复习昨日 HashSet 不允许重复元素,无序 HashSet去重原理: 先比较hashco…...
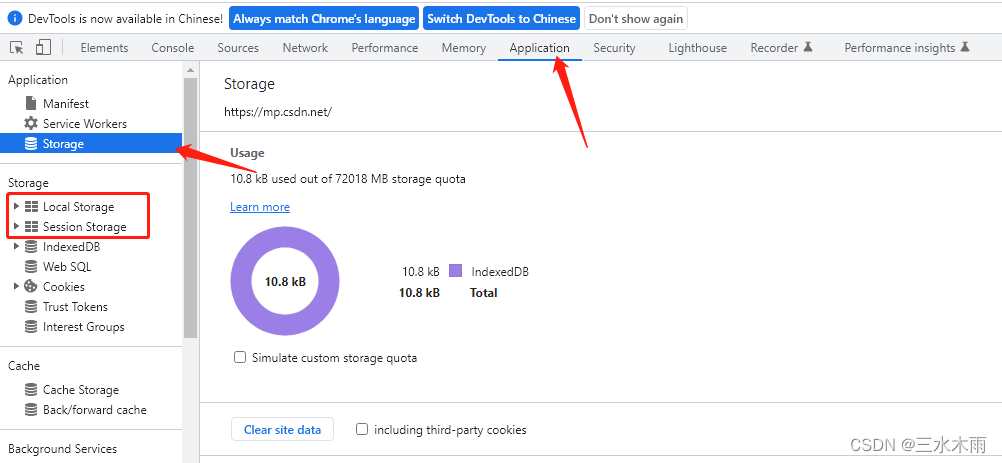
localStorage和sessionStorage
目录 一、localStorage和SessionStorage在哪里,是什么 二、localStorage和sessionStorage区别 三、localStorage常用方法 四、sessionStorage常用方法 一、localStorage和SessionStorage在哪里,是什么 【1】在浏览器开发者工具的Application栏目里&…...
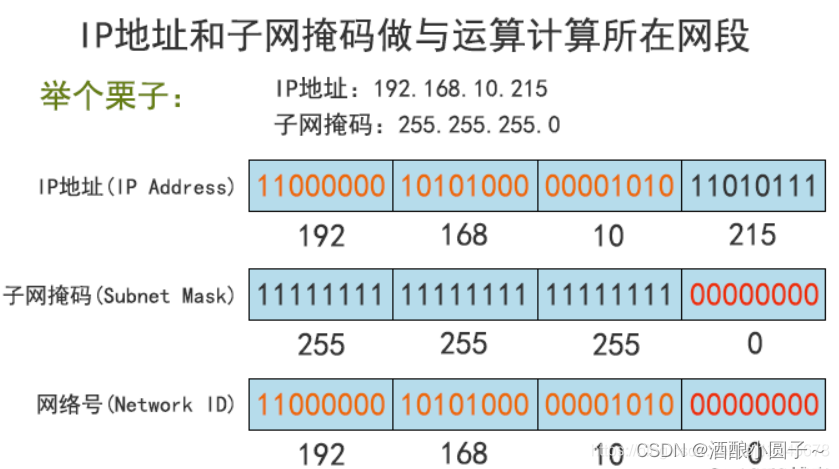
IP地址,子网掩码,网段 概念详解
文章目录1. 子网掩码1.1 子网掩码的概念及作用1.2 子网掩码的组成1.3 子网掩码的表示方法1.4 为什么要使用子网掩码?1.5 子网掩码的分类2. 子网掩码和IP地址的关系2.1 根据掩码确定网段IP地址是以 网络号和 主机号来标示网络上的主机的,我们把网络号相同…...

数影周报:动视暴雪疑似数据泄露,数据出境安全评估申报最新进展
本周看点:动视暴雪疑似员工敏感信息及游戏数据泄露;谷歌云计算部门:两名员工合用一个工位;数据出境安全评估申报最新进展;TikTok Shop东南亚商城在泰国和菲律宾公布;智己汽车获九大金融机构50亿元贷款签约.…...

Web安全最详细学习路线指南,从入门到入职(含书籍、工具包)
在这个圈子技术门类中,工作岗位主要有以下三个方向: 安全研发 安全研究:二进制方向 安全研究:网络渗透方向 下面逐一说明一下. 第一个方向:安全研发 你可以把网络安全理解成电商行业、教育行业等其他行业一样&#x…...

ChatGPT?听说Biying把它下架了
ChatGPT被玩疯了,开始放飞自我 ChatGPT版微软必应上线不到10天…就被网友玩坏了 先说这个词,放飞自我,什么东西才会放飞自我? 人放飞自我,人?你确定是人? 所以让我们来把上面的句子改写一下。…...
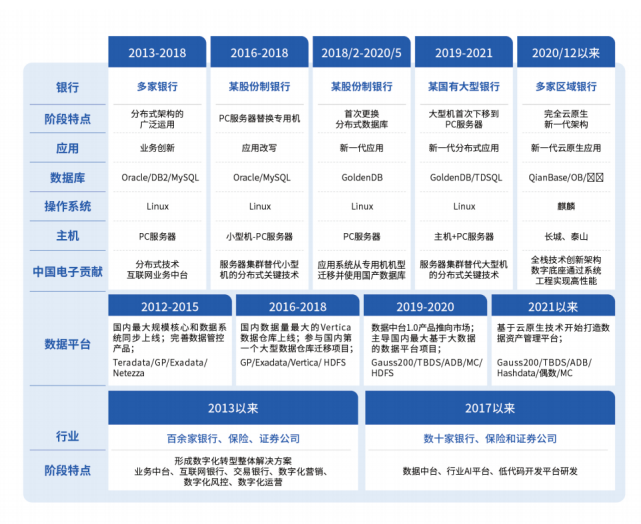
中电金信:金融数字化转型路在何方?这里有答案
近期,媒体大数网整合了业内10份研究报告,详解金融数字化转型的思路、方法与路径。其中「中国电子金融级数字底座“源启”白皮书」也被收录其中。让我们一同阅读文章,探究金融数字化转型相关问题的答案吧。 当前,金融科技正在回归…...

【Leedcode】数据结构中链表必备的面试题(第五期)
【Leedcode】数据结构中链表必备的面试题(第五期) 文章目录【Leedcode】数据结构中链表必备的面试题(第五期)1.题目2.思路图解(1)第一步:复制每一个结点,插入到原结点和下一个结点之…...

ECDH secp256k1 集成
在Android 原生api是不支持secp256k1算法的,所以要先集成以下库:implementation com.madgag.spongycastle:core:1.58.0.0compile com.madgag.spongycastle:prov:1.54.0.0compile com.madgag.spongycastle:pkix:1.54.0.0compile com.madgag.spongycastle:…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...
