创新学习方式,电大搜题助您迈向成功之路

近年来,随着信息技术的发展,互联网在教育领域发挥的作用越来越显著。贵州开放大学作为国内首家电视大学,一直致力于创新教学模式,帮助学生更好地获取知识。在学习过程中,学生常常遇到疑难问题,而解决这些问题既需要时间精力,也需要准确的答案支持。幸运的是,电大搜题微信公众号的出现,为广大贵州开放大学的学生提供了一个便捷高效的解题平台。
作为电大搜题微信公众号的用户,您将享受到无与伦比的学习体验。电大搜题凭借其强大的题库资源和智能算法,能够帮助学生快速找到答案,并提供详细而清晰的解题思路。不论是复习备考还是课程知识点的理解,都能在电大搜题中找到理想的解决方案。而且,通过电大搜题,学生们之间也能够进行互助交流,分享学习心得,共同提高。
贵州开放大学以其优质的教育资源而闻名于世。然而,传统的学习模式却存在一定的局限性。学生们往往需要手动整理资料和答案,耗费大量的时间和精力。而有了电大搜题,一切都变得简单起来。通过智能搜索功能,学生们只需输入关键词,便能快速找到相关的解题答案。这种高效的学习方式不仅有助于提高学习效率,而且对节约学习时间也起到了重要的作用。
电大搜题微信公众号的便捷性也为学生们带来了极大的方便。只需打开微信,扫码关注电大搜题公众号,便能随时随地进行解题搜索。不再需要借助笔记本电脑或纸质学习资料,学生们可以在手机上轻松查找答案,进行多次反复的学习演练。这种便利的学习方式不论是在宿舍还是在外出旅行时,都能够满足学生的学习需求。
除了强大的学习功能,电大搜题微信公众号还定期更新学习资讯和技巧,为学生们提供更多的学业辅导和指导。通过关注公众号,学生们能够了解到最新的学习动态和资源分享,以及一些学习技巧和心得。这种学习交流平台不仅丰富了学生们的学习内容,还增强了学生之间的交流和互动。
在电大搜题微信公众号的帮助下,贵州开放大学的学生们能够更加高效地学习,更好地解决学习难题,为顺利完成学业打下坚实的基础。电大搜题的搭建不仅为学生们提供了学习的利器,也彰显了贵州开放大学的创新精神和教育理念。
让我们一起加入电大搜题微信公众号,共同迈向成功之路!让学习变得简单、高效!
相关文章:

创新学习方式,电大搜题助您迈向成功之路
近年来,随着信息技术的发展,互联网在教育领域发挥的作用越来越显著。贵州开放大学作为国内首家电视大学,一直致力于创新教学模式,帮助学生更好地获取知识。在学习过程中,学生常常遇到疑难问题,而解决这些问…...

Mybatis整理
Mybatis 定义 Mybatis是一个半ORM(对象关系映射)框架,它内部封装了JDBC,加载驱动、创建连接、创建statement等繁杂的过程,开发者开发时只需要关注如何编写SQL语句,可以严格控制sql执行性能,灵…...

pytorch定义datase多次重复采样
有的时候训练需要对样本重复抽样为一个batch,可以按如下格式定义: class TrainLoader(Dataset):def __init__(self, fns, repeat1):super(TrainLoader, self).__init__()self.length len(fns) # 数据数量self.repeat repeat # 数据重复次数def __getitem__(self,…...
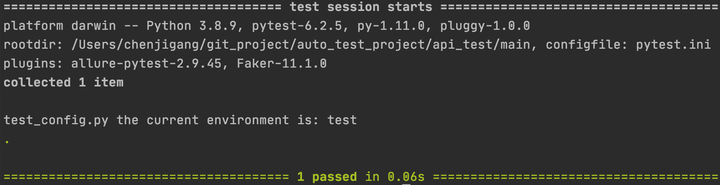
自动化测试 —— Pytest fixture及conftest详解!
前言 fixture是在测试函数运行前后,由pytest执行的外壳函数。fixture中的代码可以定制,满足多变的测试需求,包括定义传入测试中的数据集、配置测试前系统的初始状态、为批量测试提供数据源等等。fixture是pytest的精髓所在,类似u…...

Nginx解析漏洞
常见的解析漏洞: IIS 5.x/6.0解析漏洞 IIS 7.0/IIS 7.5/ Nginx <0.8.3畸形解析漏洞 Nginx <8.03 空字节代码执行漏洞 Apache解析漏洞 Nginx文件解析漏洞 对于任意文件名,例如:cd.jpg在后面添加/x.php后,即可将文件作为php解析。 原理…...
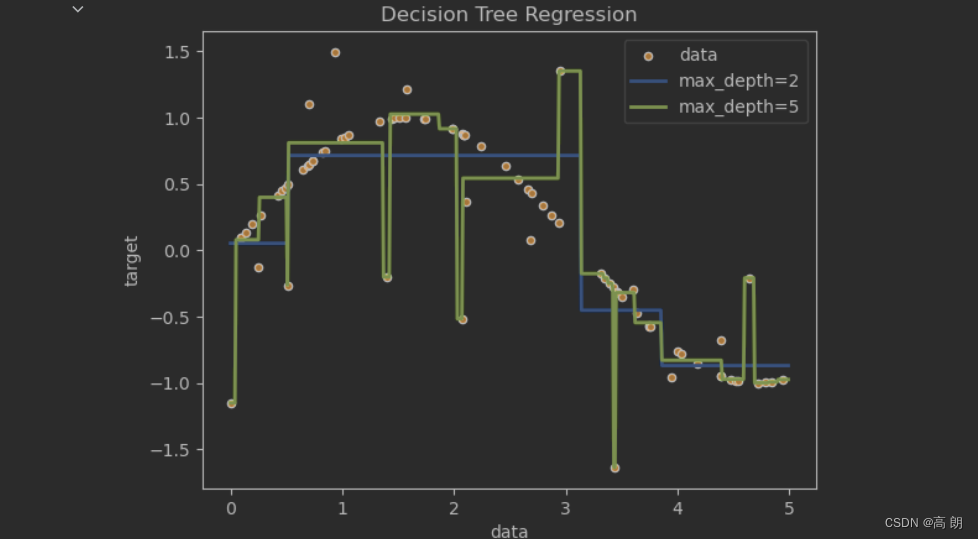
【机器学习】决策树原理及scikit-learn使用
文章目录 决策树详解ID3 算法C4.5算法CART 算法 scikit-learn使用分类树剪枝参数重要属性和接口 回归树重要参数,属性及接口交叉验证代码示例 一维回归的图像绘制 决策树详解 决策树(Decision Tree)是一种非参数的有监督学习方法,…...
系统时钟)
#基于一个小车项目的FREERTOS分析(一)系统时钟
系统时钟 //初始化延迟函数 //SYSTICK的时钟固定为AHB时钟,基础例程里面SYSTICK时钟频率为AHB/8 //这里为了兼容FreeRTOS,所以将SYSTICK的时钟频率改为AHB的频率! //SYSCLK:系统时钟频率 /* 系统定时器是一个 24bit 的向下递减的计数器&…...
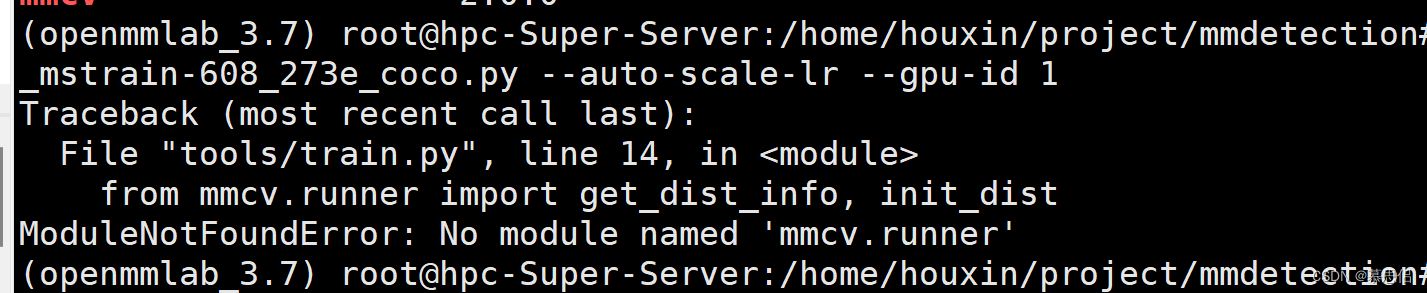
ubuntu mmdetection配置
mmdetection配置最重要的是版本匹配,特别是cuda,torch与mmcv-full 本项目以mmdetection v2.28.2为例介绍 1.查看显卡算力 因为gpu的算力需要与Pytorch依赖的CUDA算力匹配,低版本GPU可在相对高的CUDA版本下运行,相反则不行 算力…...

嵌入式面试常见问题(一)
目录 1.什么情况下会出现段错误? 2.swap() 函数为什么不能交换两个变量的值 3.一个函数有六个参数 分别放在哪个区? 4.定义一个变量,赋初值和不赋初值分别保存在哪个区? 5.linux查看端口状态的命令 6.结构体中->和.的区…...

docker批量删除本地镜像
docker rmi -f $(docker images|grep docker|awk {print $3})...
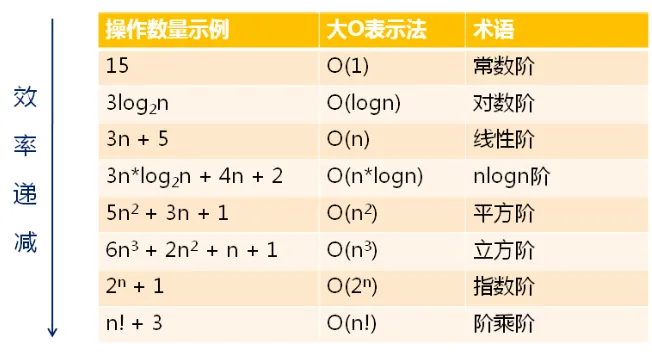
数据结构(一)—— 数据结构简介
文章目录 一、基本概念和术语?1.1、数据1.2、数据元素1.3、数据项(属性、字段)1.4、数据对象1.5、数据结构 二、逻辑结构和物理结构(存储结构)2.1、逻辑结构1、定义2、分类(线性结构和非线性结构࿰…...
Ubuntu输入正确密码重新跳到登录界面
Ubuntu输入正确密码重新跳到登录界面 问题描述 输入正确的密码登录后闪一下又回到锁屏界面 输入正确的密码后还是回到这个界面 产生的原因 /etc/profile或者/etc/enviroment出现了问题,导致无法正常登录 该错误产生的原因不止一个 这里是因为/etc/profile或者/etc/enviromen出…...

TCP/IP(十四)流量控制
一 流量控制 说明: 本文只是原理铺垫,没有用tcpdumpwiresahrk鲜活的案例讲解,后续补充 ① 基本概念 流量控制: TCP 通过接受方实际能接收的数据量来控制发送方的窗口大小 ② 正常传输过程 背景:1、客户端是接收方,服务端是发送方 --> 下载2、假设接收窗…...

CSS网页标题图案和LOGO SEO优化
favicon图标 将网页的头名字旁边放入一个图案 想将想要的图案切成png图片 然后把png图片转换成ico图案可以借助进行访问 将语法引用到head里面 SEO译为搜索引擎优化。是一种利用搜索引擎的规则提高网站有关搜索引擎的自然排名的方式 SEO的目的是对网站进行深度的优化&…...

机器人制作开源方案 | 双轮提升搬运小车
1. 功能描述 双轮提升搬运小车是一种用于搬运和移动物体的机械设备,它通常采用双轮驱动和提升装置。一般具备以下特点: ① 双轮驱动:该小车配备两个驱动轮,通过电动机或其它动力源驱动,提供足够的动力和扭矩࿰…...

5G安卓核心板-MT6833/MT6853核心板规格参数
随着智能手机的不断发展,芯片技术在推动手机性能和功能方面发挥着关键作用。MT6833和MT6853安卓核心板是两款高度集成的基带平台,为LTE/5G/NR和C2K智能手机应用提供强大的处理能力和多样化的接口。 这两款安卓核心板都集成了蓝牙、FM、WLAN和GPS模块&…...
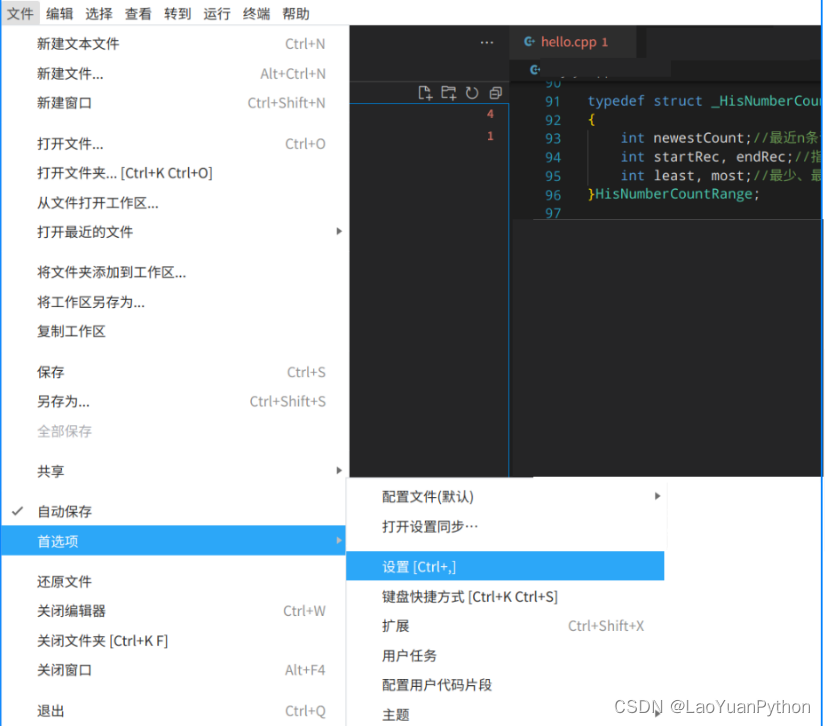
信创之国产浪潮电脑+统信UOS操作系统体验4:visual studio code中怎么显示中文
☞ ░ 前往老猿Python博客 ░ https://blog.csdn.net/LaoYuanPython 一、引言 今天在vscode中打开以前的一段C代码,其中的中文显示为乱码,如图所示: 而在统信文本编辑器打开是正常的,打开所有菜单,没有找到相关配置…...
Magica Cloth 使用方法笔记
Magica Cloth 使用方法笔记 效果展示: 参考资料: 1、官方使用文档链接: インストールガイド – Magica Soft 2、鱼儿效果案例: https://www.patreon.com/posts/69459293 3、插件工具链接:版本() 目录:…...

c++ 学习之 强制类型转换运算符 const_cast
看例子怎么用 int main() {int a 1;int* p a;// 会发生报错// 如果学着 c的风格类型转换int* pp (int*)a;*pp 1; // 编译不报错,但是运行报错// const_castconst int n 5;const std::string s "lalal";// const cast 只针对指针,引用&…...
)
Ceph相关部署应用(博客)
这里写目录标题 Ceph相关部署应用一.存储基础1.单机存储设备2.商业存储解决方案3.分布式存储(软件定义的存储 SDS) 二.Ceph 简介1.Ceph2.Ceph 优势3.Ceph 架构4.Ceph 核心组件5.OSD 存储后端6.Ceph 数据的存储过程7.Ceph 版本发行生命周期8.Ceph 集群部署…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
