简单多状态dp【动态规划】
目录
一、按摩师
二、打家劫舍
三、删除并获得点数
四、粉刷房子
五、买卖股票的最佳时机
六、买卖股票的最佳时机(含手续费)
七、买卖股票的最佳时机III
八、买卖股票的最佳时机IV
一、按摩师

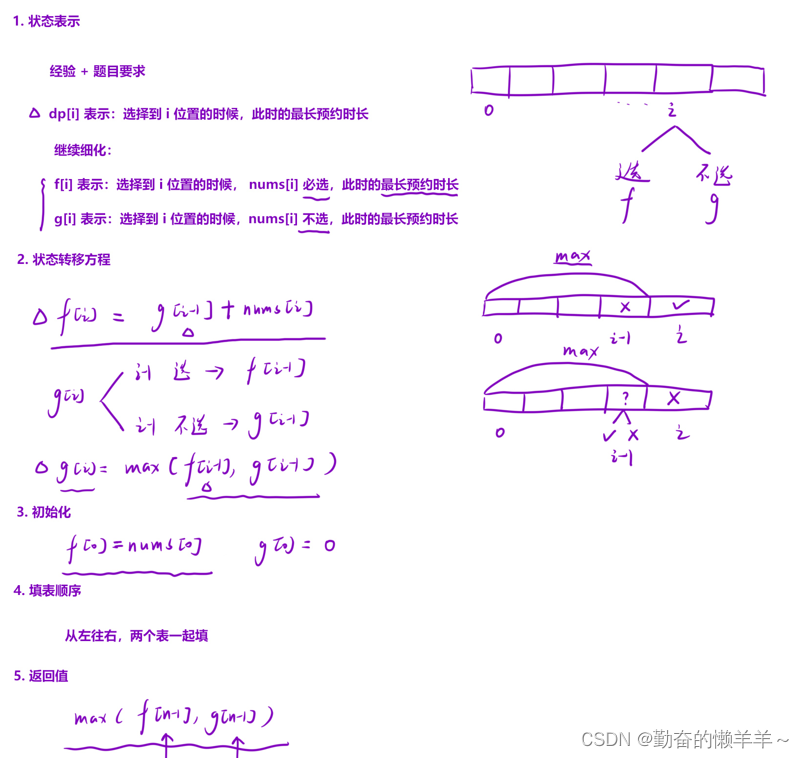
class Solution { public:int massage(vector<int>& nums) {int n =nums.size();if(n == 0) return 0;vector<int> f(n);auto g = f;f[0] = nums[0];for(int i = 1;i < n;i++){f[i] = g[i-1] + nums[i];g[i] = max(f[i-1],g[i-1]);}return max(f[n-1],g[n-1]);} };
二、打家劫舍


class Solution {
public:int rob1(vector<int>& nums,int l,int r) {if(l>r) return 0;int n =nums.size();if(n == 0) return 0;vector<int> f(n);auto g = f;f[l] = nums[l];for(int i = l;i <= r;i++){f[i] = g[i-1] + nums[i];g[i] = max(f[i-1],g[i-1]);}return max(f[r],g[r]);}int rob(vector<int>& nums) {int n = nums.size();int ret1 = rob1(nums,2,n-2)+nums[0];int ret2 = rob1(nums,1,n-1);return max(ret1,ret2);}
};三、删除并获得点数

class Solution {
public:int deleteAndEarn(vector<int>& nums) {int n = nums.size();const int N = 10001;int arr[N] = {0}; for(auto e : nums){arr[e] += e;}vector<int> f(N);auto g = f;for(int i = 1;i < N;i++){f[i] = g[i-1] + arr[i];g[i] = max(f[i-1],g[i-1]);}return max(f[N-1],g[N-1]);}
};四、粉刷房子



class Solution {
public:int minCost(vector<vector<int>>& costs) {int n = costs.size();vector<vector<int>> dp(n+1,vector<int>(3));for(int i = 1;i <= n;i++){dp[i][0] = costs[i-1][0] + min(dp[i-1][1],dp[i-1][2]);dp[i][1] = costs[i-1][1] + min(dp[i-1][0],dp[i-1][2]);dp[i][2] = costs[i-1][2] + min(dp[i-1][0],dp[i-1][1]);}return min(dp[n][0],min(dp[n][1],dp[n][2]));}
};五、买卖股票的最佳时机




class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n,vector<int>(3));dp[0][0] = -prices[0];for(int i = 1;i < n;i++){dp[i][0] = max(dp[i-1][0],dp[i-1][1] - prices[i]);dp[i][1] = max(dp[i-1][1],dp[i-1][2]);dp[i][2] = dp[i-1][0]+prices[i];}return max(dp[n-1][1],dp[n-1][2]);}
};六、买卖股票的最佳时机(含手续费)
上一题用的是二维数组的第二维来表示多种状态,是因为状态比较多,如果像此题只有两种状态,就可以用两个函数,本质上是一样的。



class Solution {
public:int maxProfit(vector<int>& prices, int fee) {int n = prices.size();vector<int> f(n);auto g = f;f[0] = -prices[0];for(int i = 1;i < n;i++){f[i] = max(f[i-1],g[i-1] - prices[i]);g[i] = max(g[i-1],f[i-1]+prices[i]- fee);}return g[n-1];}
};七、买卖股票的最佳时机III


class Solution {
public:const int INF = 0x3f3f3f3f;int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> f(n,vector<int>(3,-INF));auto g = f;f[0][0] = -prices[0];g[0][0] = 0;for(int i = 1;i < n;i++){for(int j = 0;j < 3;j++){f[i][j] = max(f[i-1][j],g[i-1][j] - prices[i]);g[i][j] = g[i-1][j];if(j >= 1)g[i][j] = max(g[i-1][j],f[i-1][j-1]+prices[i]);}} int ret = 0;for(int i = 0;i < 3;i++){ret = max(ret,g[n-1][i]);}return ret;}
};八、买卖股票的最佳时机IV

class Solution {
public:int maxProfit(int k, vector<int>& prices) {int n = prices.size();k = min(k,n/2); const int INF = 0x3f3f3f3f;vector<vector<int>> f(n,vector<int>(k+1,-INF));//注意是k+1auto g = f;f[0][0] = -prices[0];g[0][0] = 0;for(int i = 1;i < n;i++){for(int j = 0;j <= k;j++){f[i][j] = max(f[i-1][j],g[i-1][j]-prices[i]);g[i][j] = g[i-1][j];if(j >= 1)g[i][j] = max(g[i-1][j],f[i-1][j-1]+prices[i]);}}int ret = 0;for(int j = 0;j <= k;j++){ret = max(ret,g[n-1][j]);}return ret;}
};相关文章:

简单多状态dp【动态规划】
目录 一、按摩师 二、打家劫舍 三、删除并获得点数 四、粉刷房子 五、买卖股票的最佳时机 六、买卖股票的最佳时机(含手续费) 七、买卖股票的最佳时机III 八、买卖股票的最佳时机IV 一、按摩师 class Solution { public:int massage(vector<int>…...

OpenCV中initUndistortRectifyMap ()函数与十四讲中去畸变公式的区别探究
文章目录 1.十四讲中的去畸变公式2. OpenCV中的去畸变公式3. 4个参数和8个参数之间的区别4.initUndistortRectifyMap()函数源码 最近在使用OpenCV对鱼眼相机图像去畸变时发现一个问题,基于针孔模型去畸变时所使用的参数和之前十四讲以及视觉SLAM中的畸变系数有一点不…...

【C++】C++11——智能指针、内存泄漏、智能指针的使用和原理、RAII、auto_ptr、unique_ptr、shared_ptr、weak_ptr
文章目录 C117.智能指针7.1内存泄漏7.2智能指针的概念7.3智能指针的使用7.3.1 auto_ptr7.3.2 unique_ptr7.3.3 shared_ptr7.3.4 weak_ptr C11 7.智能指针 7.1内存泄漏 什么是内存泄漏: 内存泄漏指因为疏忽或错误造成程序未能释放已经不再使用的内存的情况。内存泄漏…...

EDUSRC-记某擎未授权与sql注入
目录 360天擎 - 未授权与sql注入 信息收集 FOFA语法 鹰图搜索 360天擎未授权访问 - 数据库信息泄露 漏洞复现 修复方案 360天擎终端安全管理系统ccid处SQL注入 漏洞复现 手动测试方法 修复方案 360天擎 - 未授权与sql注入 通常访问的页面如下,存在登录框…...

1688拍立淘API接口分享
拍立淘接口,顾名思义,就是通过图片搜索到相关商品列表。通过此接口,可以实现图片搜索爆款商品等功能。 接口地址:1688.item_search_img 公共参数 名称类型必须描述keyString是调用key(必须以GET方式拼接在URL中&…...

昇腾910使用记录
一. 压缩文件和解压文件 1. 压缩文件 tar -czvf UNITE-main.tar.gz ./UNITE-main/2. 解压文件 tar -xvf ./UNITE-main/二. CUDA更改为NPU data[label] data[label].cuda() data[instance] data[instance].cuda() data[image] data[image].cuda()更改为 data[label] da…...
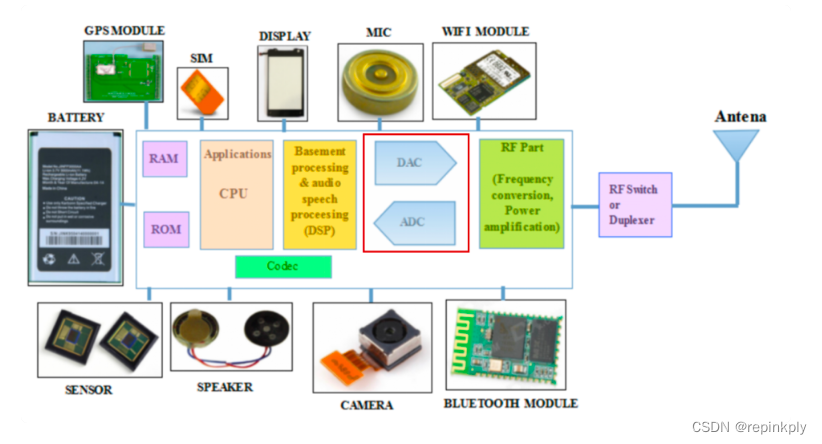
从一部iPhone手机看芯片的分类
目录 问题 iPhone X 手机处理器:A11 iPhone X 的两大存储芯片 数字 IC CPU:计算设备的运算核心和控制核心 GPU:图形处理器 ASIC:为解决特定应用问题而定制设计的集成电路 存储芯片:DRAM 和 NAND Flash iPhone…...

arm day 7
完成字符串收发函数的封装并且验证现象,一个字符串发送接受后会有‘\n’ \r src/uart.c #include"uart.h"void uart4_init() {//设置UART4的RCc时钟使能//RCC_MP_APB1ENSETR[16]->1RCC->MP_APB1ENSETR | (0x1<<16);//设置GPIOB和GPIOG的时钟…...

Java基础面试-面向对象
什么是面向对象? 对比面向过程,是两种不同的处理问题角度 面向过程更注重事情的每一个步骤及顺序,面向对象更注重事情有哪些参与者(对象),及各自需要做什么 比如洗衣机洗衣服 面向过程会将任务拆解成一系…...

GCC vs. G++:C 与 C++ 编译器的差异和比较
本文将介绍 GCC(GNU Compiler Collection)和 G 编译器的区别,并对它们在 C 和 C 程序开发中的特性和用法进行比较和总结。 引言 在 C 和 C 程序开发中,选择合适的编译器是至关重要的。GCC(GNU Compiler Collection&a…...

MAC m系列docker login报错
错误:ERROR: failed to solve: XXX error getting credentials - err: exit status 1, out: 解决: vi ~/.docker/config.jsonzsxzsx [15时55分55秒] [~] { {"auths": {"harbor-g42c.corp.matrx.team": {"auth": "…...

Redis通用指令和五大基本数据类型常用指令总结
通用指令 keys parttern 查询key (parttern即通配符,不是正则表达式,例如 keys a? 匹配以a开头的长度为2的key) del key 删除key exists key 获取key是否存在 type key 获取key的类型 expire key seconds 为指定key设置有效期,单位秒 …...

uCharts常用图表组件demo
带渐变阴影的曲线图 <view class"charts-box"><qiun-data-charts type"area" :opts"opts" :chartData"chartData" :ontouch"true":background"rgba(256,256,256,0)" /> </view>data(){return{…...
VNC:Timed out waiting for a response from the computer
VNC的服务端使用的是TigerVNC,客户端使用的是RealVNC TigerVNC按其他博客配好后,防火墙ip什么的都配了,vnc客户端怎么连都是超时。 这里建议大家可以尝试一下重启服务器。我的是CentOS的 shutdown -r now 配了2天,最后服务器重启…...

Kotlin 协程 知识点
Android 上的 Kotlin 协程 | Android Developers (google.cn) 官方网址 1.什么是协程? 我觉得协程就是kotlin中一种优雅的实现异步请求 协程(Coroutines)是一种轻量级的并发编程概念,旨在简化异步编程和并发任务的处理。它是…...

简单大方的自我介绍 PPT 格式
自我介绍是展示自己的机会,同时也是展现自信和魅力的重要时刻。通过简单大方的PPT格式,可以更好地展示自己的个性和才华。下面是一些建议,帮助你在自我介绍中展现自信和魅力。 1. 打造简洁而有吸引力的PPT布局: - 选择简洁大方的背…...
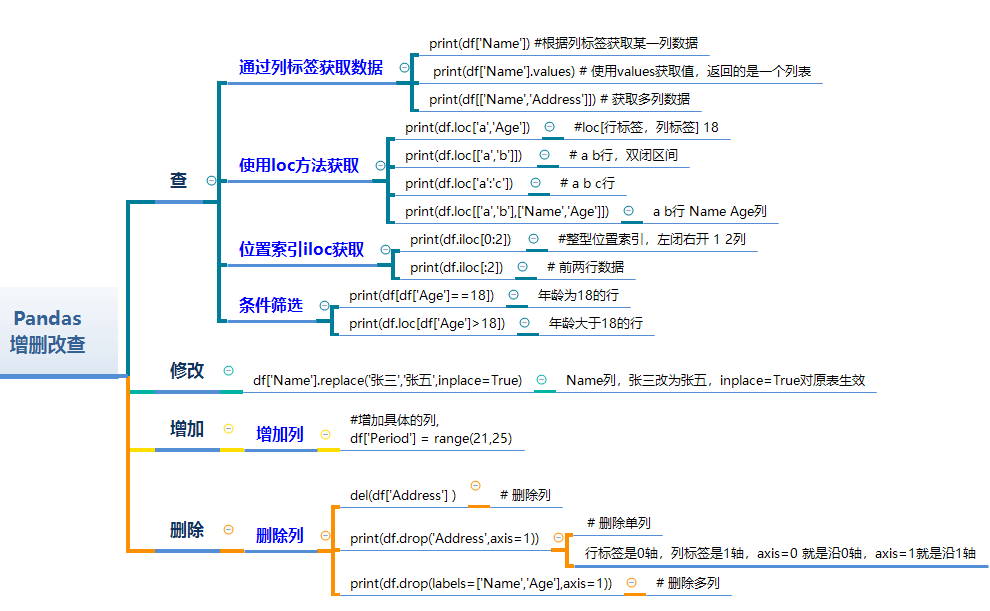
panads操作excel
panads简介 pandas是基于Numpy创建的Python包,内置了大量标准函数,能够高效地解决数据分析数据处理和分析任务,pandas支持多种文件的操作,比如Excel,csv,json,txt 文件等,读取文件之…...

【MySQL】联合查询、子查询、合并查询
这里提供了三个表: 表1: mysql> select * from class; -------------- | id | name | -------------- | 1 | 一班 | | 2 | 二班 | | 3 | 三班 | -------------- 3 rows in set (0.01 sec) 表2: mysql> select * fro…...
小程序中如何设置所服务地区的时区
在全球化的背景下,小程序除了在中国使用外,还为海外的华人地区提供服务。例如我们采云小程序为泰国、阿根廷、缅甸等国家的商家就提供过微信小程序。这些商家开通小程序,为本地的华人提供服务。但通常小程序的开发者/服务商位于中国ÿ…...

Linux环境安装mysql8.0
1个人习惯我喜欢给软件安装在/use/local下,我使用的finalshell软件,直接手动新建一个文件夹名字为mysql 2下载mysql wget https://dev.mysql.com/get/Downloads/MySQL-8.0/mysql-8.0.20-linux-glibc2.12-x86_64.tar.xz 3解压文件 tar -xvf mysql-8.0.2…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
