【算法优选】 二分查找专题——贰
文章目录
- 😎前言
- 🌲[山脉数组的峰顶索引](https://leetcode.cn/problems/peak-index-in-a-mountain-array/)
- 🚩题目描述:
- 🚩算法思路
- 🚩代码实现:
- 🌴[寻找峰值](https://leetcode.cn/problems/find-peak-element/submissions/)
- 🚩题目描述
- 🚩算法思路:
- 🚩代码实现
- 🍀[寻找旋转排序数组中的最小值](https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array/)
- 🚩题目描述
- 🚩算法思路
- 🚩代码实现
- 🎍[点名](https://leetcode.cn/problems/que-shi-de-shu-zi-lcof/)
- 🚩题目描述
- 🚩思路解析
- 🚩代码实现
- ⭕总结
😎前言
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
查找过程:
首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
算法要求:
1.必须采用顺序存储结构。
2.必须按关键字大小有序排列。
比较次数:
计算公式:
当顺序表有n个关键字时:
查找失败时,至少比较a次关键字;
查找成功时,最多比较关键字次数是b。
注意:a,b,n均为正整数。
算法复杂度:
二分查找的基本思想是将n个元素分成大致相等的两部分,取a[n/2]与x做比较,如果x=a[n/2],则找到x,算法中止;如果x<a[n/2],则只要在数组a的左半部分继续搜索x,如果x>a[n/2],则只要在数组a的右半部搜索x.
时间复杂度即是while循环的次数。
总共有n个元素,
渐渐跟下去就是n,n/2,n/4,…n/2^k(接下来操作元素的剩余个数),其中k就是循环的次数
由于你n/2^k取整后>=1
即令n/2^k=1
可得k=log2n,(是以2为底,n的对数)
所以时间复杂度可以表示O(h)=O(log2n)
🌲山脉数组的峰顶索引
🚩题目描述:
符合下列属性的数组 arr 称为 山脉数组 :
arr.length >= 3
存在 i(0 < i < arr.length - 1)使得:
-
arr[0] < arr[1] < … arr[i-1] < arr[i]
-
arr[i] > arr[i+1] > … > arr[arr.length - 1]
给你由整数组成的山脉数组 arr ,返回满足 arr[0] < arr[1] < … arr[i - 1] < arr[i] > arr[i + 1] > … > arr[arr.length - 1] 的下标 i 。
你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。
-
示例 1:
输入:arr = [0,1,0]
输出:1 -
示例 2:
输入:arr = [0,2,1,0]
输出:1 -
示例 3:
输入:arr = [0,10,5,2]
输出:1
class Solution {public int peakIndexInMountainArray(int[] arr) {}
}
🚩算法思路
1、分析峰顶位置的数据特点,以及⼭峰两旁的数据的特点:
-
峰顶数据特点: arr[i] > arr[i - 1] && arr[i] > arr[i + 1] ;
-
峰顶左边的数据特点: arr[i] > arr[i - 1] && arr[i] < arr[i + 1] ,也就是呈现上升趋势
-
峰顶右边数据的特点: arr[i] < arr[i - 1] && arr[i] > arr[i + 1] ,也就是呈现下降趋势
2.、因此,根据 mid 位置的信息,我们可以分为下⾯三种情况:
-
如果 mid 位置呈现上升趋势,说明我们接下来要在 [mid + 1, right] 区间继续搜索;
-
如果 mid 位置呈现下降趋势,说明我们接下来要在 [left, mid - 1] 区间搜索;
-
如果 mid 位置就是⼭峰,直接返回结果
🚩代码实现:
class Solution {public int peakIndexInMountainArray(int[] arr) {int left = 1;int right = arr.length - 2;while(left < right) {int mid = left + (right - left + 1) / 2;if(arr[mid] > arr[mid - 1]) {left = mid;} else {right = mid - 1;}}return left;}
}
🌴寻找峰值
🚩题目描述
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
- 示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。 - 示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;或者返回索引 5, 其峰值元素为 6。
class Solution {public int findPeakElement(int[] nums) {}
}
🚩算法思路:
寻找⼆段性:
任取⼀个点 i ,与下⼀个点 i + 1 ,会有如下两种情况:
-
arr[i] > arr[i + 1] :此时「左侧区域」⼀定会存在⼭峰(因为最左侧是负⽆穷),那么我们可以去左侧去寻找结果;
-
arr[i] < arr[i + 1] :此时「右侧区域」⼀定会存在⼭峰(因为最右侧是负⽆穷),那么我们可以去右侧去寻找结果
当我们找到「⼆段性」的时候,就可以尝试⽤「⼆分查找」算法来解决问题
🚩代码实现
class Solution {public int findPeakElement(int[] nums) {int left = 0;int right = nums.length - 1;if(right < 1) {return 0;}while(left < right) {int cmd = (left + right + 1) / 2;if(nums[cmd -1] <= nums[cmd] ) {left = cmd;} else {right = cmd -1;}}return left;}
}
🍀寻找旋转排序数组中的最小值
🚩题目描述
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
- 若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
-
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。 -
示例 2:
输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。 -
示例 3:
输入:nums = [11,13,15,17]
输出:11
解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组
class Solution {public int findMin(int[] nums) {}
}
🚩算法思路
题⽬中的数组规则如下图所⽰:
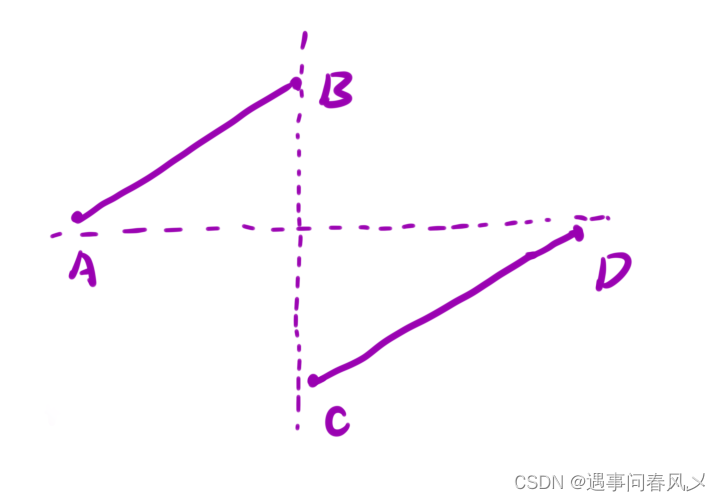
其中 C 点就是我们要求的点。
⼆分的本质:找到⼀个判断标准,使得查找区间能够⼀分为⼆。
通过图像我们可以发现, [A,B] 区间内的点都是严格⼤于 D 点的值的, C 点的值是严格⼩于 D 点的值的。但是当 [C,D] 区间只有⼀个元素的时候, C 点的值是可能等于 D 点的值的。
因此,初始化左右两个指针 left , right :
然后根据 mid 的落点,我们可以这样划分下⼀次查询的区间:
- 当 mid 在 [A,B] 区间的时候,也就是 mid 位置的值严格⼤于 D 点的值,下⼀次查询区间在 [mid + 1,right] 上;
- 当 mid 在 [C,D] 区间的时候,也就是 mid 位置的值严格⼩于等于 D 点的值,下次
查询区间在 [left,mid] 上。
当区间⻓度变成 1 的时候,就是我们要找的结果
🚩代码实现
class Solution {public int findMin(int[] nums) {int left = 0;int right = nums.length - 1;int cmp = nums[right];while(left < right) {int cmd = (left + right ) / 2;if(nums[cmd] > cmp) {left = cmd + 1;} else {right = cmd;}}return nums[left];}
}
🎍点名
🚩题目描述
某班级 n 位同学的学号为 0 ~ n-1。点名结果记录于升序数组 records。假定仅有一位同学缺席,请返回他的学号。
-
示例 1:
输入: records = [0,1,2,3,5]
输出: 4 -
示例 2:
输入: records = [0, 1, 2, 3, 4, 5, 6, 8]
输出: 7
🚩思路解析
关于这道题中,时间复杂度为 O(N) 的解法有很多种,⽽且也是⽐较好想的,这⾥就不再赘述。
本题只讲解⼀个最优的⼆分法,来解决这个问题。
在这个升序的数组中,我们发现:
-
在第⼀个缺失位置的左边,数组内的元素都是与数组的下标相等的;
-
在第⼀个缺失位置的右边,数组内的元素与数组下标是不相等的。
因此,我们可以利⽤这个「⼆段性」,来使⽤「⼆分查找」算法。
🚩代码实现
class Solution {public int missingNumber(int[] nums) {int left = 0;int right = nums.length - 1;while(left < right) {int mid = left + (right - left) / 2;if(nums[mid] == mid) {left = mid + 1;} else {right = mid;}}return left == nums[left] ? left + 1 : left;}
}
⭕总结
关于《【算法优选】 二分查找专题——贰》就讲解到这儿,感谢大家的支持,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下!
相关文章:

【算法优选】 二分查找专题——贰
文章目录 😎前言🌲[山脉数组的峰顶索引](https://leetcode.cn/problems/peak-index-in-a-mountain-array/)🚩题目描述:🚩算法思路🚩代码实现: 🌴[寻找峰值](https://leetcode.cn/pro…...

SQL 的优化
SQL 优化是指对数据库查询语句进行优化,以提高查询性能和效率。下面列出了一些常见的 SQL 优化技巧: 1、索引优化 (1)使用适当的索引来加速查询操作。在频繁用于查询的列上创建索引,特别是在 WHERE 条件、JOIN 条件和…...

华为云云耀云服务器L实例评测|华为云上的CentOS性能监测与调优指南
目录 引言 编辑1 性能调优的基本要素 2 性能监控功能 2.1 监控数据指标 2.2 数据历史记录 2.3 多种统计指标 3 性能优化策略 3.1 资源分配 3.2 磁盘性能优化 3.3 网络性能优化 3.4 操作系统参数和内核优化 结论 引言 在云计算时代,性能优化和调优对于…...

Go If流程控制与快乐路径原则
Go if流程控制与快乐路径原则 文章目录 Go if流程控制与快乐路径原则一、流程控制基本介绍二、if 语句2.1 if 语句介绍2.2 单分支结构的 if 语句形式2.3 Go 的 if 语句的特点2.3.1 分支代码块左大括号与if同行2.3.2 条件表达式不需要括号 三、操作符3.1 逻辑操作符3.2 操作符的…...

yolov8 strongSORT多目标跟踪工具箱BOXMOT
1 引言 多目标跟踪MOT项目在Github中比较完整有:BOXMOT , 由mikel brostrom提供。在以前的版本中,有yolov5deepsort(版本v3-v5), yolov8strongsort(版本v6-v9),直至演变…...

如何开发一款跑酷游戏?
跑酷游戏(Parkour Game)是一种流行的视频游戏类型,玩家需要在游戏中控制角色进行极限动作、跳跃、爬墙和各种动作,以完成各种挑战和任务。如果你有兴趣开发一款跑酷游戏,以下是一些关键步骤和考虑事项: 游…...
使用宝塔面板在Linux上搭建网站,并通过内网穿透实现公网访问
文章目录 前言1. 环境安装2. 安装cpolar内网穿透3. 内网穿透4. 固定http地址5. 配置二级子域名6. 创建一个测试页面 前言 宝塔面板作为简单好用的服务器运维管理面板,它支持Linux/Windows系统,我们可用它来一键配置LAMP/LNMP环境、网站、数据库、FTP等&…...

Unity可视化Shader工具ASE介绍——6、通过例子说明ASE节点的连接方式
大家好,我是阿赵。继续介绍Unity可视化Shader编辑插件ASE的用法。上一篇已经介绍了很多ASE常用的节点。这一篇通过几个小例子,来看看这些节点是怎样连接使用的。 这篇的内容可能会比较长,最终是做了一个遮挡X光的效果,不过把这…...
VUE3基础知识梳理
VUE3基础知识梳理 一、vue了解和环境搭建1.vue是什么:cn.vuejs.org/vuejs.org2.渐进式框架3.vue的版本4.vueAPI的风格5.准备环境5.1.创建vue项目5.2.vue的目录结构 二、vue3语法1.干净的vue项目2.模板语法2.1 文本插值2.2属性绑定2.3条件渲染2.4列表渲染2.5通过key管…...

Java架构师缓存通用设计方案
目录 1 采用多级缓存2 缓存数据尽量前移3 静态化4 数据平衡策略5 jvm缓存的问题6 redis存放数据解决7 redis垂直拆分8 总结1 采用多级缓存 在实际应用中需要考虑的实际问题。首先,前端页面可以做缓存,虽然图上没有显示,但在现实应用中这是提高性能的一个重要方面。前端页面缓…...
2023年【危险化学品生产单位安全生产管理人员】及危险化学品生产单位安全生产管理人员模拟考试题
题库来源:安全生产模拟考试一点通公众号小程序 危险化学品生产单位安全生产管理人员考前必练!安全生产模拟考试一点通每个月更新危险化学品生产单位安全生产管理人员模拟考试题题目及答案!多做几遍,其实通过危险化学品生产单位安…...
微信小程序 在bindscroll事件中监听scroll-view滚动到底
scroll-view其实提供了一个 bindscrolltolower 事件 这个事件的作用是直接监听scroll-view滚动到底部 但是 总有不太一样的情况 公司的项目 scroll-view 内部 最下面有一个 类名叫 bottombj 的元素 我希望 滚动到这个 bottombj 上面的时候就开始加载滚动分页 简单说 bottombj这…...
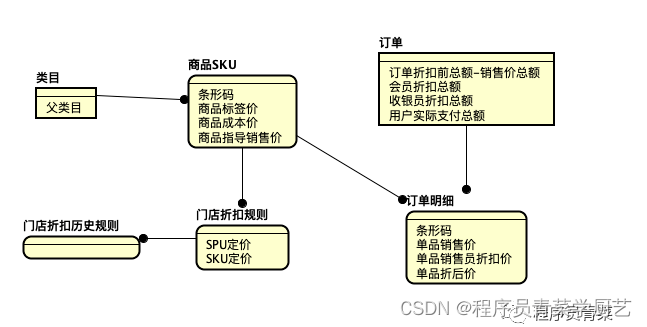
收银系统商品定价设计思考
一、背景 因为门店系统里商品总共也就几万款,一直以来都是根据条码由总部统一定价销售,现在有加盟店,各门店也有进行各自促销活动的需求,这就需要放开门店自主定价权,所以近段时间系统在商品定价上做了扩展。 二、商…...
Kotlin函数作为参数指向不同逻辑
Kotlin函数作为参数指向不同逻辑 fun sum(): (Int, Int) -> Int {return { a, b -> (a b) } }fun multiplication(): (Int, Int) -> Int {return { a, b -> (a * b) } }fun main(args: Array<String>) {var math: (Int, Int) -> Intmath sum()println(m…...

读书笔记—《如何阅读一本书》
读书笔记—《如何阅读一本书》 一、阅读的层次1、主动阅读的基础一个阅读者要提出的四个基本问题 2、基础阅读(第一层)3、检视阅读(第二层)4、分析阅读(第三层) 二、阅读不同读物的方法三、阅读的最终目标1…...

Kafka数据同步原理详解
Kafka数据同步原理详解 Kafka是一种分布式的消息队列系统,它具有高吞吐量、可扩展性和分布式特性等优势。在Kafka中,数据按照主题进行分区,每个主题都有一组分区。每个分区都有自己的生产者和消费者,生产者负责向分区中写入消息&…...

C++课程总复习
一、c的第一条程序 1.cout cout >输出类对象,用来输出的,可以自动识别类型,所以不需要加格式符号 << 插入符(输出符号) endl 换行>\n #include <iostream> //#预处理 //include 包含 相应的头…...

数据结构—顺序表
目录 1.线性表 2.顺序表概念 3.实现顺序表 (1)声明结构体 (2)初始化 (3)打印数据 (4) 销毁 (5)尾插&头插 尾插 判断是否扩容 头插 (6)尾删&头删 尾删 头删 (7)指定位置插入元素 (8)删除指定位置元素 (9)查找指定元素位置 (10)修改指定位置元素 完整版…...

企业服务器租用对性能有什么要求呢?
企业租用服务器租用首要的是稳定,其次是安全,稳定是为了让企业的工作能够顺利进行,只有性能稳定的服务器才能保证网站之类的正常工作,就让小编带大家看一看有什么要求吧! 服务器简单介绍。服务器是在网络上为其它客户机…...

2731.移动机器人
2731. 移动机器人 - 力扣(LeetCode) 有一些机器人分布在一条无限长的数轴上,他们初始坐标用一个下标从 0 开始的整数数组 nums 表示。当你给机器人下达命令时,它们以每秒钟一单位的速度开始移动。 给你一个字符串 s ,…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
