Beam Focusing for Near-Field Multi-User MIMO Communications阅读笔记
abstract
大天线阵列和高频段是未来无线通信系统的两个关键特征。大规模天线与高传输频率的组合通常导致通信设备在近场(菲涅耳)区域中操作。在本文中,我们研究了潜在的波束聚焦,可行的近场操作,在促进高速率多用户下行链路多输入多输出(MIMO)系统。由于实现波束聚焦的能力是由发射天线决定的,我们研究了考虑不同的天线结构的近场信令,包括全数字架构,混合移相器为基础的预编码器,和新兴的动态元表面天线(DMA)架构的大规模MIMO阵列。我们首先提供了一个数学模型来表征近场无线信道以及所考虑的天线架构的传输模式。然后,我们制定波束聚焦问题的目标,最大化可实现的和速率在多用户网络。我们提出了有效的解决方案的基础上的和速率最大化任务的全数字,(基于移相器的)混合和DMA架构。仿真结果表明,所提出的波束聚焦方案的单用户和多用户场景的可行性。特别地,所设计的聚焦波束提供了新的自由度以减轻角度域和距离域两者中的干扰,这是使用常规远场波束转向无法实现的,从而允许甚至驻留在相同角度方向上的使用的可靠通信。
system model
在本节中,我们描述所考虑的近场多用户MIMO通信系统。我们首先在第II-A节中介绍近场传输的概念。然后,我们在第II-B节中制定了近场无线信道的数学模型。之后,我们在第II-C节中提出了三种类型的天线架构及其对应的信号模型。最后,在第II-D节中,我们制定了设计传输波束方向图的优化问题,以最大化近场通信的总速率。
近场域
根据常规符号,如果发射器和接收器之间的距离大于夫琅和费距离,则认为发射发生在远场中,由 d F = 2 D 2 λ d_{\mathrm{F}}=\frac{2 D^{2}}{\lambda} dF=λ2D2表示,其中 D D D是天线直径, λ \lambda λ是波长。对于大于 d F d_{\mathrm{F}} dF的距离,信号波前可以被faithfully近似为平面。当距离短于 d F d_{\mathrm{F}} dF但大于菲涅耳距离(通常由 d N = D 4 8 λ 3 d_{\mathrm{N}}=\sqrt[3]{\frac{D^{4}}{8 \lambda}} dN=38λD4表示)时,接收器被认为位于辐射近场菲涅耳区域中,此后称为近场区域 。近场占 d F d_{\mathrm{F}} dF和 d N d_{\mathrm{N}} dN之间的距离。边界 d N d_{\mathrm{N}} dN构成来自天线本身的无功场分量(reactive field components)可以被忽略的最小距离。
传统的无线通信由于所需的距离、天线尺寸和频率而处于远场中。例如,对于在5GHz的载波频率下直径 D = 0.1 D = 0.1 D=0.1米的天线,位于大于 d F = 0.33 d_{\mathrm{F}} = 0.33 dF=0.33米的距离处的任何接收器被认为位于远场中。然而,对于毫米波频带,特别是当与相对大的物理尺寸的天线阵列组合时,这种近似不再成立,并且必须考虑球面波阵面形状。这一点在Fig1中得到了证明, 其示出了用于不同天线直径 D D D和载波频率 f 0 f_0 f0的 d F d_{\mathrm{F}} dF(上限)和 d N d_{\mathrm{N}} dN(下限)的值,其一起界定预期的近场操作区域。从图1中,我们可以清楚地看到,当系统工作在毫米波频段时,对于相对较小的天线/表面,近场距离可以高达几十米。例如,对于在载波频率28 GHz处配备有直径D = 0.5米的天线的BS,距离天线小于47米的任何用户驻留在其近场中。因此,研究如何利用近场不可忽略的球面波阵面来提高通信速率是很有意义的。特别地,这产生了产生聚焦波束的可能性,并通过减轻多用户干扰来增强无线网络的通信性能。
近场信道模型
为了评估利用MIMO通信中的近场操作的能力,我们专注于下行链路多用户系统。特别地,我们考虑下行链路多用户MIMO系统,其中BS采用均匀平面阵列(UPA),即,二维天线表面,在水平方向上具有 N e N_e Ne个均匀间隔的辐射元件,在垂直方向上具有 N d N_d Nd个元件。因此,天线元件的总数为 N = N d × N e N = N_d × N_e N=Nd×Ne。我们将第i行的第l个元素的笛卡尔坐标表示为 p i , l = ( x l , y i , 0 ) , l = 1 , 2 ⋯ N e , i = 1 , 2 , ⋯ , N d \mathbf{p}_{i,l} =(x_l,y_i,0), l = 1,2 \cdots N_e, i = 1, 2, \cdots, N_d pi,l=(xl,yi,0),l=1,2⋯Ne,i=1,2,⋯,Nd。BS与 M M M个单天线接收机通信,如图2所示。我们认为接收器的定位信息在BS处通过高精度无线定位技术已知[3]。我们专注于近场通信,即其中BS和用户之间的距离不大于夫琅和费距离 d F d_F dF并且不小于菲涅耳极限 d N d_N dN。近场球面波的性质允许产生聚焦波束以促进通信。
首先,我们按照辐射近场中的EM传播的现有建模技术对近场无线信道进行建模,例如,[30]第30段。第 m m m个用户在自由空间条件下接收的信号, m ∈ M ≜ { 1 , 2 , … , M } m \in \mathcal{M} \triangleq\{1,2, \ldots, M\} m∈M≜{1,2,…,M},位于 p m = ( x m , y m , z m ) \mathbf{p}_{m}=\left(x_{m}, y_{m}, z_{m}\right) pm=(xm,ym,zm)处,由下式给出:
r ( p m ) = ∑ i = 1 N d ∑ l = 1 N e A i , l ( p m ) e − ȷ k ∣ p m − p i , l ∣ s i , l + n m (1) r\left(\mathbf{p}_{m}\right)=\sum_{i=1}^{N_{d}} \sum_{l=1}^{N_{e}} A_{i, l}\left(\mathbf{p}_{m}\right) e^{-\jmath k\left|\mathbf{p}_{m}-\mathbf{p}_{i, l}\right|} s_{i, l}+n_{m} \tag{1} r(pm)=i=1∑Ndl=1∑NeAi,l(pm)e−k∣pm−pi,l∣si,l+nm(1)
其中 s i , l s_{i, l} si,l表示由位置 p i , l \mathbf{p}_{i, l} pi,l处的天线发射的信号;术语 e − ȷ k ∣ p m − p i , l ∣ e^{-\jmath k\left|\mathbf{p}_{m}-\mathbf{p}_{i, l}\right|} e−k∣pm−pi,l∣包含由于波从 p i , l \mathbf{p}_{i, l} pi,l到 p m \mathbf{p}_{m} pm行进的距离而产生的相位; k = 2 π / λ k=2 \pi / \lambda k=2π/λ为波数( wave number); A i , l ( p m ) A_{i, l}\left(\mathbf{p}_{m}\right) Ai,l(pm)表示信道增益系数;并且, n m ∼ C N ( 0 , σ 2 ) n_{m} \sim \mathcal{C N}\left(0, \sigma^{2}\right) nm∼CN(0,σ2)是用户 m m m处的加性高斯白噪声(AWGN)。在[30]之后,我们写
A i , l ( p m ) = F ( Θ i , l , m ) λ 4 π ∣ p m − p i , l ∣ (2) A_{i, l}\left(\mathbf{p}_{m}\right)=\sqrt{F\left(\Theta_{i, l, m}\right)} \frac{\lambda}{4 \pi\left|\mathbf{p}_{m}-\mathbf{p}_{i, l}\right|} \tag{2} Ai,l(pm)=F(Θi,l,m)4π∣pm−pi,l∣λ(2)
其中 Θ i , l , m = ( θ i , l , m , ϕ i , l , m ) \Theta_{i, l, m}=\left(\theta_{i, l, m}, \phi_{i, l, m}\right) Θi,l,m=(θi,l,m,ϕi,l,m)是从第 i i i行的第 l l l个元素到第 m m m个用户的仰角-方位角对,而 F ( Θ i , l , m ) F\left(\Theta_{i, l, m}\right) F(Θi,l,m)是每个元素的辐射分布,建模为
F ( Θ i , l , m ) = { 2 ( b + 1 ) cos b ( θ i , l , m ) θ i , l , m ∈ [ 0 , π / 2 ] 0 otherwise. (3) F\left(\Theta_{i, l, m}\right)=\left\{\begin{array}{ll} 2(b+1) \cos ^{b}\left(\theta_{i, l, m}\right) & \theta_{i, l, m} \in[0, \pi / 2] \\ 0 & \text { otherwise. } \end{array}\right. \tag{3} F(Θi,l,m)={2(b+1)cosb(θi,l,m)0θi,l,m∈[0,π/2] otherwise. (3)
在(3)中,参数 b b b确定瞄准线增益(Boresight gain),其值取决于所采用的特定技术[30]。作为示例,对于偶极子情况,我们具有 b = 2 b = 2 b=2,其产生(服从) F ( Θ i , l , m ) = 6 cos 2 θ i , l , m F\left(\Theta_{i, l, m}\right)=6 \cos ^{2} \theta_{i, l, m} F(Θi,l,m)=6cos2θi,l,m。在这里,该模型考虑了发射功率被天线后面的反射面加倍的事实。
为了获得(1)中接收信号的更紧凑的公式,我们定义向量:
a m = [ A 1 , 1 ( p m ) e − ȷ k ∣ p m − p 1 , 1 ∣ , A 1 , 2 ( p m ) e − ȷ k ∣ p m − p 1 , 2 ∣ ⋯ , A N d , N e ( p m ) e − ȷ k ∣ p m − p N d , N e ∣ ] H (4) \begin{aligned} \mathbf{a}_{m}=[ & A_{1,1}\left(\mathbf{p}_{m}\right) e^{-\jmath k\left|\mathbf{p}_{m}-\mathbf{p}_{1,1}\right|}, A_{1,2}\left(\mathbf{p}_{m}\right) e^{-\jmath k\left|\mathbf{p}_{m}-\mathbf{p}_{1,2}\right|} \\ & \left.\cdots, A_{N_{d}, N_{e}}\left(\mathbf{p}_{m}\right) e^{-\jmath k\left|\mathbf{p}_{m}-\mathbf{p}_{N_{d}, N_{e}}\right|}\right]^{H} \end{aligned} \tag{4} am=[A1,1(pm)e−k∣pm−p1,1∣,A1,2(pm)e−k∣pm−p1,2∣⋯,ANd,Ne(pm)e−k∣pm−pNd,Ne∣]H(4)
为了方便起见,我们在本文的其余部分省略了 a m ( p m ) \mathbf{a}_m(\mathbf{p}_m) am(pm)中的位置索引 p m \mathbf{p}_m pm。使用(4),我们然后可以将在第 m m m个用户处接收到的信号写为
r ( p m ) = a m H s + n m , m ∈ M (5) r\left(\mathbf{p}_{m}\right)=\mathbf{a}_{m}^{H} \mathbf{s}+n_{m}, \quad m \in \mathcal{M} \tag{5} r(pm)=amHs+nm,m∈M(5)
其中 s = [ s 1 , 1 , s 1 , 2 ⋯ , s N d , N e ] \mathbf{s}=\left[s_{1,1}, s_{1,2} \cdots, s_{N_{d}, N_{e}}\right] s=[s1,1,s1,2⋯,sNd,Ne]收集所有天线的发射信号。
近场操作被封装在(4)中定义的向量 a m \mathbf{a}_m am中。当远场近似成立时,所有元件的输出经历相同的路径损耗(例如, A ( p m ) = A i , l ( p m ) ∀ i , l A\left(\mathbf{p}_{m}\right)=A_{i, l}\left(\mathbf{p}_{m}\right) \forall i, l A(pm)=Ai,l(pm)∀i,l),以及沿着阵列孔径具有恒定梯度的相移,其中 Θ i , l , m = Θ m ∀ i , l \Theta_{i, l, m}=\Theta_{m} \forall i, l Θi,l,m=Θm∀i,l。更具体地, a m \mathbf{a}_m am变成由 a m = A ( p m ) [ e − j k Ψ 1 , 1 ( Θ m ) , … , e − j k Ψ i , l ( Θ m ) , … , e − j k Ψ N d , N e ( Θ m ) ] \mathbf{a}_m = A\left(\mathbf{p}_{m}\right)\left[e^{-j k \Psi_{1,1}\left(\Theta_{m}\right)}, \ldots, e^{-j k \Psi_{i, l}\left(\Theta_{m}\right)}, \ldots, e^{-j k \Psi_{N_{d}, N_{e}}\left(\Theta_{m}\right)}\right] am=A(pm)[e−jkΨ1,1(Θm),…,e−jkΨi,l(Θm),…,e−jkΨNd,Ne(Θm)]给出的传统波束控制向量,其中 Ψ i , 1 ( Θ m ) \Psi_{i, 1}\left(\Theta_{m}\right) Ψi,1(Θm)仅取决于第 m m m个用户的方向和辐射元件之间的间距。近场中 a m \mathbf{a}_m am的元素之间的多样性产生了将波束朝向空间中的预期位置聚焦的可能性,而不是如在远场中所实现的那样仅以给定角度操纵波束。
天线结构
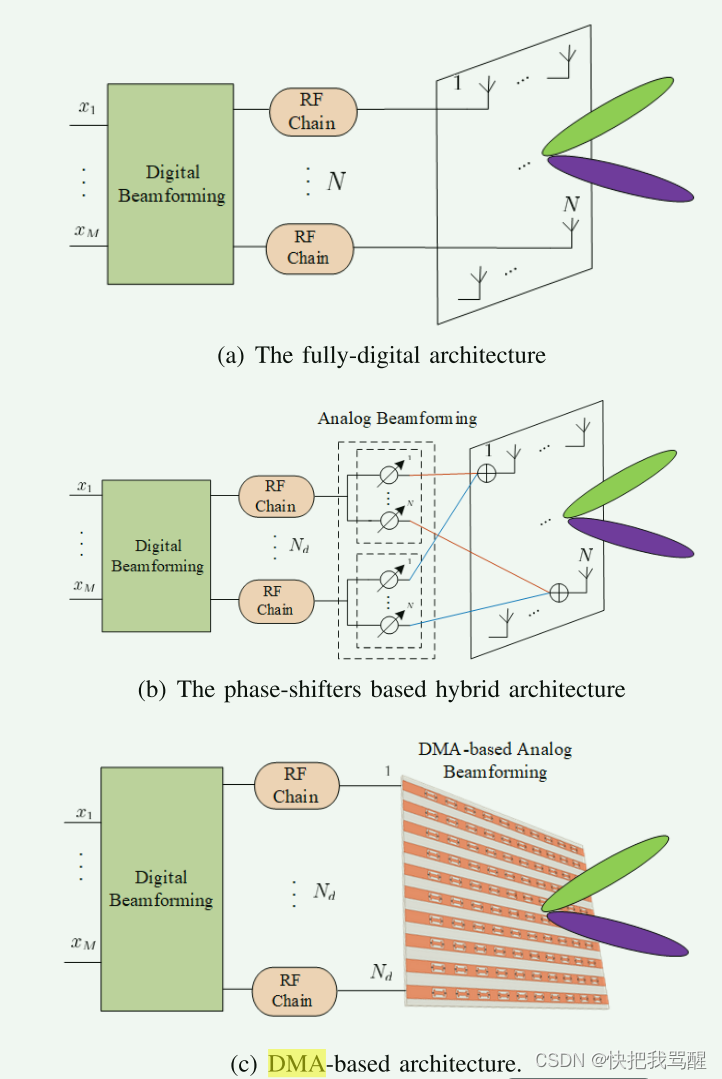
全数字天线
在全数字天线中,每个元件都连接到专用射频链,如图 3(a) 所示。这种架构提供了最灵活的信号处理能力,因为每个元件的输入都可以单独处理。尽管如此,全数字天线通常成本高昂,特别是在大规模 MIMO 系统中,因为射频链的数量等于天线元件的数量 [19]、[20]。因此,我们将全数字架构视为基线系统,代表在具有无约束线性预编码的近场多用户通信中可实现的波束聚焦能力。在这种情况下,BS发送的信号可以写为
s = ∑ m = 1 M w ~ m x m (6) \mathbf{s}=\sum_{m=1}^{M} \tilde{\mathbf{w}}_{m} x_{m} \tag{6} s=m=1∑Mw~mxm(6)
where x m x_{m} xm is the normalized data symbol intended for the m m m th user, i.e., E [ x m 2 ] = 1 \mathbb{E}\left[x_{m}^{2}\right]=1 E[xm2]=1 , and w ~ m ∈ C N \tilde{\mathbf{w}}_{m} \in \mathbb{C}^{N} w~m∈CN is the precoding vector for x m x_{m} xm .
通过(6)表示信道输入 s \mathbf{s} s,第 m m m个用户的接收信号为:
r ( p m ) = a m H ∑ j = 1 M w ~ j x j + n m , m ∈ M (7) r\left(\mathbf{p}_{m}\right)=\mathbf{a}_{m}^{H} \sum_{j=1}^{M} \tilde{\mathbf{w}}_{j} x_{j}+n_{m}, \quad m \in \mathcal{M} \tag{7} r(pm)=amHj=1∑Mw~jxj+nm,m∈M(7)
根据 (7),全数字天线情况下第 m m m 个用户的可实现速率由下式给出
R m ( { w ~ m } ) = log 2 ( 1 + ∣ a m H w ~ m ∣ 2 ∑ j ≠ m ∣ a m H w ~ j ∣ 2 + σ 2 ) , m ∈ M (8) R_{m}\left(\left\{\tilde{\mathbf{w}}_{m}\right\}\right)=\log _{2}\left(1+\frac{\left|\mathbf{a}_{m}^{H} \tilde{\mathbf{w}}_{m}\right|^{2}}{\sum_{j \neq m}\left|\mathbf{a}_{m}^{H} \tilde{\mathbf{w}}_{j}\right|^{2}+\sigma^{2}}\right), \quad m \in \mathcal{M} \tag{8} Rm({w~m})=log2(1+∑j=m∣amHw~j∣2+σ2 amHw~m 2),m∈M(8)
表达式(8)表征了给定预编码配置下每个用户可实现的速率,并且假设用户将干扰视为噪声来计算。虽然在某些场景中可以通过解码干扰来实现更高的速率[31],但下行链路大规模 MIMO 系统的常见做法是将其视为噪声[32],从而得到(8)中的速率。
基于相移的混合天线
DMA(dynamic metasurface antennas)
DMA利用嵌入到波导表面上的辐射超材料元件来实现低成本和功耗的可重构天线[24]。典型的DMA架构由多个波导组成,例如在一些实施例中,微带包括多个超材料元件,并且每个微带包含多个超材料元件。元件通常是亚波长间隔开的,这意味着与基于例如贴片阵列[24]。每个单独元件的频率响应可以通过改变其局部电气特性来外部调节[33]。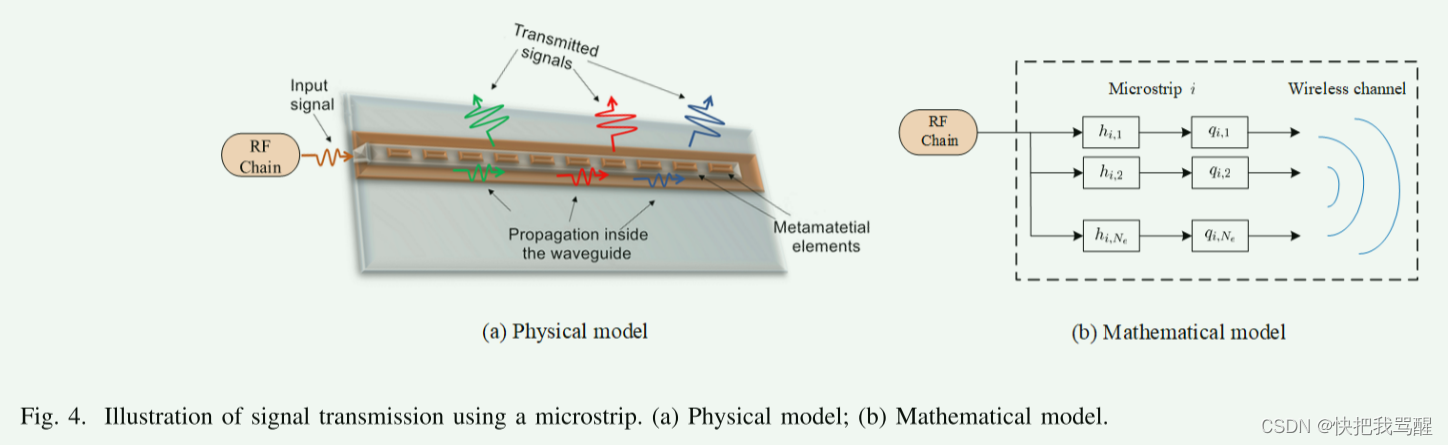
对于基于DMA的发射架构,每个微带由一个RF链馈电,并且输入信号由位于微带上的所有元件辐射,如Fig3c所示。图4示出了使用具有多个元件的单个微带传输信号的示例。为了用公式表示其输入-输出关系,考虑由 N = N d ⋅ N e N = N_d · N_e N=Nd⋅Ne超材料元件组成的DMA,其中 N d N_d Nd和 N e N_e Ne分别是微带和每个微带中的元件的数量。从第 i i i个微带的第 l l l个元件辐射的等效基带信号是 s i , l = h i , l q i , l z i s_{i, l}=h_{i, l} q_{i, l} z_{i} si,l=hi,lqi,lzi,其中 z i z_i zi是馈送到第 i i i个微带的基带信号, q i , l q_{i,l} qi,l表示第 i i i个微带的第 l l l个元件的可调谐响应,并且 h i , l h_{i,l} hi,l封装了微带内部的信号传播的影响。我们考虑元件的响应是频率平坦的情况,如[21]中所示,并且关注超材料元件频率响应的洛伦兹约束相位模型[34]、[35],即,
q i , l ∈ Q ≜ { j + e j ϕ 2 ∣ ϕ ∈ [ 0 , 2 π ] } , ∀ i , l (11) q_{i, l} \in \mathcal{Q} \triangleq\left\{\frac{j+e^{j \phi}}{2} \mid \phi \in[0,2 \pi]\right\}, \forall i, l \tag{11} qi,l∈Q≜{2j+ejϕ∣ϕ∈[0,2π]},∀i,l(11)
微带内的信号传播公式为:
h i , l = e − ρ i , l ( α i + j β i ) , ∀ i , l (12) h_{i, l}=e^{-\rho_{i, l}\left(\alpha_{i}+j \beta_{i}\right)}, \forall i, l \tag{12} hi,l=e−ρi,l(αi+jβi),∀i,l(12)
其中, α i \alpha_i αi是波导衰减系数, β i \beta_i βi是波数, ρ i , l \rho_{i,l} ρi,l表示第 i i i个微带中第 l l l个元件的位置。
Letting z = [ z 1 , … , z N d ] T \mathbf{z}=\left[z_{1}, \ldots, z_{N_{d}}\right]^{T} z=[z1,…,zNd]T be the microstrips input, the baseband representation of the signal transmitted by the DMA output is given by s = H Q z \mathbf{s}=\mathbf{H} \mathbf{Q} \mathbf{z} s=HQz , where H \mathbf{H} H is a N × N N \times N N×N diagonal matrix with elements H ( ( i − 1 ) N e + l , ( i − 1 ) N e + l ) = h i , l \mathbf{H}_{\left((i-1) N_{e}+l,(i-1) N_{e}+l\right)}=h_{i, l} H((i−1)Ne+l,(i−1)Ne+l)=hi,l , and Q ∈ C N × N d \mathbf{Q} \in \mathbb{C}^{N \times N_{d}} Q∈CN×Nd denotes the configurable weights of the DMAs, with each element given by
Q ( i − 1 ) N e + l , n = { q i , l i = n 0 i ≠ n (13) \mathbf{Q}_{(i-1) N_{e}+l, n}=\left\{\begin{array}{ll} q_{i, l} & i=n \\ 0 & i \neq n \end{array}\right. \tag{13} Q(i−1)Ne+l,n={qi,l0i=ni=n(13)
The DMA input signal is given by z = ∑ m = 1 M w m x m \mathbf{z}=\sum_{m=1}^{M} \mathbf{w}_{m} x_{m} z=∑m=1Mwmxm , where w m ∈ C N d \mathbf{w}_{m} \in \mathbb{C}^{N_{d}} wm∈CNd is the digital precoding vector for x m x_{m} xm . The baseband channel input transmitted by the DMA is thus given by s = ∑ m = 1 M H Q w m x m \mathbf{s}=\sum_{m=1}^{M} \mathbf{H Q w}_{m} x_{m} s=∑m=1MHQwmxm . We again note that the transmitted signal is formally equal to that of a fully-digital architecture with precoding vectors w ~ m = H Q w m \tilde{\mathbf{w}}_{m}=\mathbf{H Q w}_{m} w~m=HQwm for each m ∈ M m \in \mathcal{M} m∈M . Consequently, the resulting achievable rate of the m m m th user for a given DMA configuration matrix Q \mathbf{Q} Q and digital precoding vectors { w j } \left\{\mathbf{w}_{j}\right\} {wj} is computed as R m ( { H Q w j } ) R_{m}\left(\left\{\mathbf{H Q} \mathbf{w}_{j}\right\}\right) Rm({HQwj}) using (8).
问题构架
基于上述模型,我们调查多用户通信在近场,考虑到实现可靠的通信的可能性时,不同的用户共享相似的方向,但位于不同的到BS距离。这里的目的是设计传输波束图案以最大化可实现的和速率,反映每个信道使用可以可靠地传送的比特的总数。基于不同的天线架构,对于给定的发射功率约束 P m a x > 0 P_{max} > 0 Pmax>0,感兴趣的任务可以写为:
max { w ~ m } ∑ m = 1 M R m ( { w ~ j } j ∈ M ) s.t. ∑ m = 1 M ∥ w ~ m ∥ 2 ≤ P max , { w ~ m } ∈ W , (14) \begin{array}{ll} \max _{\left\{\tilde{\mathbf{w}}_{m}\right\}} & \sum_{m=1}^{M} R_{m}\left(\left\{\tilde{\mathbf{w}}_{j}\right\}_{j \in \mathcal{M}}\right) \\ \text { s.t. } & \sum_{m=1}^{M}\left\|\tilde{\mathbf{w}}_{m}\right\|^{2} \leq P_{\max }, \quad\left\{\tilde{\mathbf{w}}_{m}\right\} \in \mathcal{W}, \end{array} \tag{14} max{w~m} s.t. ∑m=1MRm({w~j}j∈M)∑m=1M∥w~m∥2≤Pmax,{w~m}∈W,(14)
其中: R m ( { w ~ j } j ∈ M ) = log 2 ( 1 + ∣ a m H w ~ m ∣ 2 ∑ j ≠ m ∣ a m H w ~ j ∣ 2 + σ 2 ) . R_{m}\left(\left\{\tilde{\mathbf{w}}_{j}\right\}_{j \in \mathcal{M}}\right)=\log _{2}\left(1+\frac{\left|\mathbf{a}_{m}^{H} \tilde{\mathbf{w}}_{m}\right|^{2}}{\sum_{j \neq m}\left|\mathbf{a}_{m}^{H} \tilde{\mathbf{w}}_{j}\right|^{2}+\sigma^{2}}\right) . Rm({w~j}j∈M)=log2(1+∑j=m∣amHw~j∣2+σ2∣amHw~m∣2).
在(14)中公式化的问题类似于在远场通信中遇到的相应问题。在近场中执行通信的事实被封装在向量 { a m } \{\mathbf{a}_m\} {am}中。因此,在续集中用于解决这个问题的一些工具是从考虑远场通信的研究中采用的。
(14)中的可行预编码向量的集合 W \mathcal{W} W捕获由天线架构施加的唯一约束:对于全数字UPA, W F D \mathcal{W}_{FD} WFD是 C N \mathbb{C}^{N} CN中所有M-向量元组的集合;对于混合波束形成器,可行集合 W H B \mathcal{W}_{HB} WHB表示为
W H B = { { w ~ m } m ∈ M ∣ w ~ m = Q w m ; Q ∈ F N × N d } (15) \mathcal{W}_{\mathrm{HB}}=\left\{\left\{\tilde{\mathbf{w}}_{m}\right\}_{m \in \mathcal{M}} \mid \tilde{\mathbf{w}}_{m}=\mathbf{Q} \mathbf{w}_{m} ; \mathbf{Q} \in \mathcal{F}^{N \times N_{d}}\right\} \tag{15} WHB={{w~m}m∈M∣w~m=Qwm;Q∈FN×Nd}(15)
For DMAs, the set of feasible precoders can be written as
W D M A = { { w ~ m } m ∈ M ∣ w ~ m = H Q w m } (16) \mathcal{W}_{\mathrm{DMA}}=\left\{\left\{\tilde{\mathbf{w}}_{m}\right\}_{m \in \mathcal{M}} \mid \tilde{\mathbf{w}}_{m}=\mathbf{H Q} \mathbf{\mathbf { w } _ { m }}\right\} \tag{16} WDMA={{w~m}m∈M∣w~m=HQwm}(16)
其中 H \mathbf{H} H是表示微带内传播的固定对角矩阵,而 Q \mathbf{Q} Q可以写成(13)中,其中非零元素取(11)中定义的 Q \mathcal{Q} Q中的值。
For both the hybrid antenna and the DMA architectures, we optimize the corresponding { w m } \left\{\mathbf{w}_{m}\right\} {wm} and Q \mathbf{Q} Q to obtain the feasible precoders { w ~ m } \left\{\tilde{\mathbf{w}}_{m}\right\} {w~m} . For the hybrid antenna, each element of Q \mathbf{Q} Q need to satisfy the unit modulus constraint in (10), whereas for the DMA, the non-zero elements of Q \mathbf{Q} Q should satisfy the Lorentzian constraint in (11).
虽然(14)的公式没有明确地考虑传输发生在近场中的事实,但是该属性被嵌入在等效信道向量 { a m } \{\mathbf{a}_m\} {am}中。如我们在后续中所示,虽然(14)中的目标函数看起来与所得波束的形状不变,但最大化近场中可实现的和速率产生聚焦光束,从而允许减轻位于相同角度方向上的用户之间的干扰。
BEAM FOCUSING AWARE PRECODING DESIGN
在本节中,我们研究波束聚焦感知预编码设计以最大化总速率。我们从第III-A节中的无约束全数字天线开始。然后,我们在第III-B节中导出混合移相器设置,并在第III-C节中考虑基于DMA的天线架构。最后,我们将在第III-D节中进行讨论。
Fully-Digital Beam Focusing
Beam Focusing via Phase-Shifters Based Hybrid Precoding
DMA-Based Beam Focusing
在这里,我们考虑用于最大化近场下行链路通信中的总速率的DMA的配置。我们注意到,在前面的小节中考虑的架构在无线通信文献中相对较好地研究,并且因此我们能够利用先前针对类似设置导出的方法来优化预编码器。然而,由于DMA用于无线通信的应用是相对新的研究领域,因此在下文中,我们基于(14)导出用于配置它们的权重的专用算法。特别地,我们首先针对 W = W D M A \mathcal{W} = \mathcal{W}_{\mathrm{DMA}} W=WDMA的情况将(14)重新表述为:
max { w m } , Q ∑ m = 1 M log 2 ( 1 + ∣ a m H H Q w m ∣ 2 ∑ j ≠ m ∣ a m H H Q w j ∣ 2 + σ 2 ) s.t. ( 13 ) , q i , l ∈ Q , ∀ i , l , ∑ M ∥ w m ∥ 2 ≤ P max . (25) \begin{array}{l} \max _{\left\{\mathbf{w}_{m}\right\}, \mathbf{Q}} \sum_{m=1}^{M} \log _{2}\left(1+\frac{\left|\mathbf{a}_{m}^{H} \mathbf{H Q} \mathbf{w}_{m}\right|^{2}}{\sum_{j \neq m}\left|\mathbf{a}_{m}^{H} \mathbf{H Q} \mathbf{w}_{j}\right|^{2}+\sigma^{2}}\right) \\ \text { s.t. } \quad(13), \quad q_{i, l} \in \mathcal{Q}, \forall i, l, \quad \sum^{M}\left\|\mathbf{w}_{m}\right\|^{2} \leq P_{\max } . \end{array} \tag{25} max{wm},Q∑m=1Mlog2(1+∑j=m∣amHHQwj∣2+σ2∣amHHQwm∣2) s.t. (13),qi,l∈Q,∀i,l,∑M∥wm∥2≤Pmax.(25)
我们注意到,(25)与(14)略有不同,因为这里的功率约束被施加在数字输出上,而不是被施加在发送的信号上。尽管如此,如前一小节中所讨论的,可以基于(25)导出整个系统,并且缩放数字预编码器,使得满足(14)中的功率约束。由于基于非凸问题(25)的DMA权重和数字预编码向量的配置的联合设计是具有挑战性的,因此我们开始考虑单用户设置以获得更多的设计见解。然后,我们的研究扩展到多用户的情况下, M > 1 M > 1 M>1,并提出了一个交替算法来处理所产生的非凸优化问题。
单用户场景
对于单用户情况,不存在用户间干扰。因此,可实现的速率由 R = log 2 ( 1 + 1 σ 2 ∣ a H H Q w ∣ 2 ) R=\log _{2}\left(1+\frac{1}{\sigma^{2}}\left|\mathbf{a}^{H} \mathbf{H Q} \mathbf{w}\right|^{2}\right) R=log2(1+σ21 aHHQw 2)给出,其中我们已经丢弃了用户索引下标 m m m。由于对数函数的单调性,优化问题(25)被等效地重写为
max w , Q ∣ a H H Q w ∣ 2 s.t. ( 13 ) , q i , l ∈ Q , ∀ i , l , ∥ w ∥ 2 ≤ P max . (26) \begin{aligned} \max _{\mathbf{w}, \mathbf{Q}} & \left|\mathbf{a}^{H} \mathbf{H Q} \mathbf{w}\right|^{2} \\ \text { s.t. } & (13), \quad q_{i, l} \in \mathcal{Q}, \forall i, l, \quad\|\mathbf{w}\|^{2} \leq P_{\max } . \end{aligned} \tag{26} w,Qmax s.t. aHHQw 2(13),qi,l∈Q,∀i,l,∥w∥2≤Pmax.(26)
尽管与(25)相比,(26)明显更容易处理,但它仍然涉及目标函数中的耦合优化变量以及非平凡的逐元素约束 Q \mathcal{Q} Q。具体地,每个元件响应 q i , l q_{i,l} qi,l应该采取(11)中的洛伦兹约束形式,其由复平面的上半部分中的圆(图11中的内圆)表示。(五)。因此, q i , l q_{i,l} qi,l的相位和振幅被耦合,这使得求解(26)具有挑战性。为了解决这个问题,我们采用[35]中提出的恒定振幅方法将洛伦兹约束放宽到具有恒定振幅和任意相位的仅相位权重约束,由 q i , l ∈ F q_{i,l} ∈ \mathcal{F} qi,l∈F给出,如(10)中定义的,对于每个 i , l i,l i,l。可行集 F \mathcal{F} F是一个以原点为中心的单位半径的圆(图五中的外圆)。
我们接下来关注问题(26),其中 Q \mathcal{Q} Q被 F \mathcal{F} F替换,并且然后使用该解决方案经由投影来调谐洛伦兹约束权重,如图5所示。由于耦合优化变量的存在,该问题仍然是非凸的。然而,我们能够以封闭形式解决它,如下面的定理所述。
Theorem 1. Let ( Q ∗ , w ∗ ) \left(\mathbf{Q}^{*}, \mathbf{w}^{*}\right) (Q∗,w∗) be the solution to (26) with Q = F \mathcal{Q}= \mathcal{F} Q=F . According to the structure constraint (13), each
non-zero element of Q ∗ \mathbf{Q}^{*} Q∗ is q i , l ∗ = e ȷ ψ i , l ∗ q_{i, l}^{*}=e^{\jmath \psi_{i, l}^{*}} qi,l∗=eψi,l∗
with ψ i , l ∗ = k ∣ p m − p i , l ∣ + β i ρ i , l \psi_{i, l}^{*}=k\left|\mathbf{p}_{m}-\mathbf{p}_{i, l}\right|+\beta_{i} \rho_{i, l} ψi,l∗=k∣pm−pi,l∣+βiρi,l and w ∗ = P max ( a H H Q ∗ ) H ∥ a H H Q ∗ ∥ \mathbf{w}^{*}=\frac{\sqrt{P_{\max }}\left(\mathbf{a}^{H} \mathbf{H} \mathbf{Q}^{*}\right)^{H}}{\left\|\mathbf{a}^{H} \mathbf{H} \mathbf{Q}^{*}\right\|} w∗=∥aHHQ∗∥Pmax(aHHQ∗)H .
从定理1中,我们可以看到,每个超材料元件的优化相位 ψ i , l ∗ \psi_{i, l}^{*} ψi,l∗包括两个部分:第一个是术语 k ∣ p − p i , l ∣ k\left|\mathbf{p}-\mathbf{p}_{i, l}\right| k∣p−pi,l∣为了实现近场聚焦,即,位置 p \mathbf{p} p中的信号分量的相干和;另一部分补偿微带中由 β i ρ i , l \beta_{i} \rho_{i, l} βiρi,l给出的传输延迟(12),使得信号被同步传输。应注意,使用全息设计过程[41]将发现类似的相位分布。
相关文章:

Beam Focusing for Near-Field Multi-User MIMO Communications阅读笔记
abstract 大天线阵列和高频段是未来无线通信系统的两个关键特征。大规模天线与高传输频率的组合通常导致通信设备在近场(菲涅耳)区域中操作。在本文中,我们研究了潜在的波束聚焦,可行的近场操作,在促进高速率多用户下…...
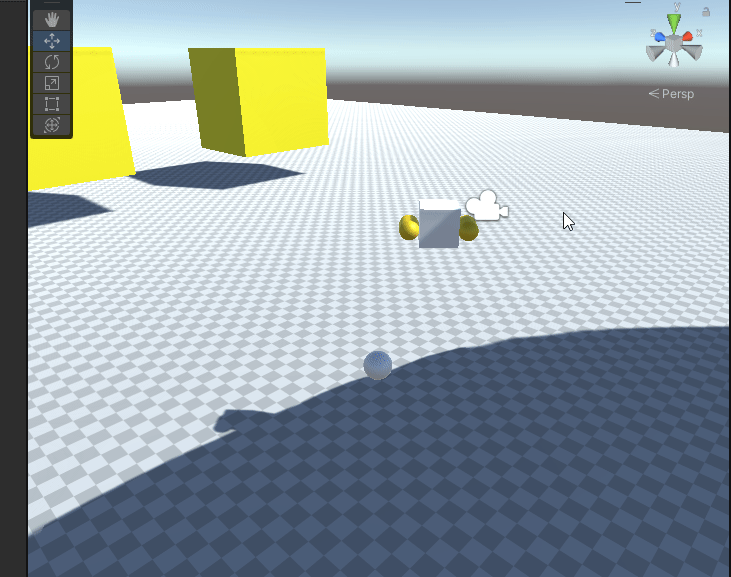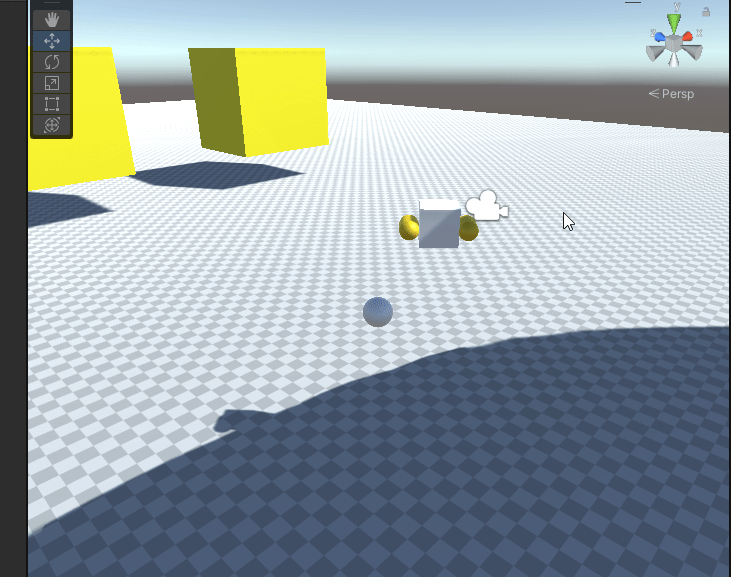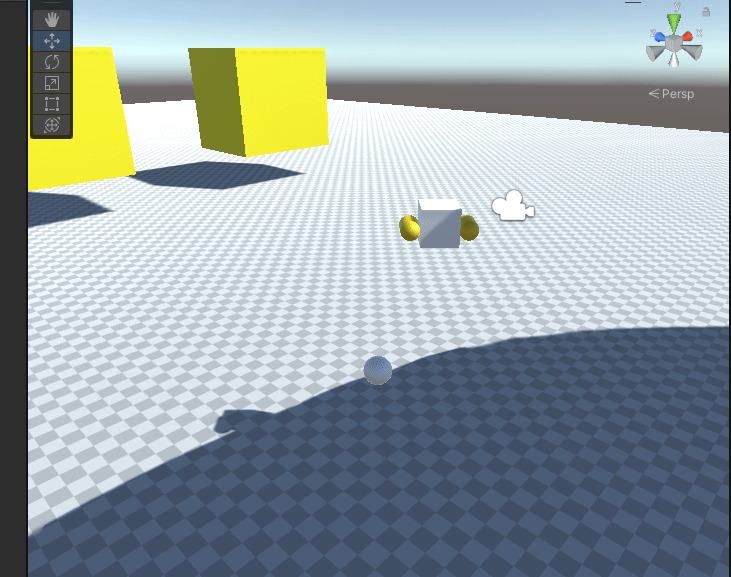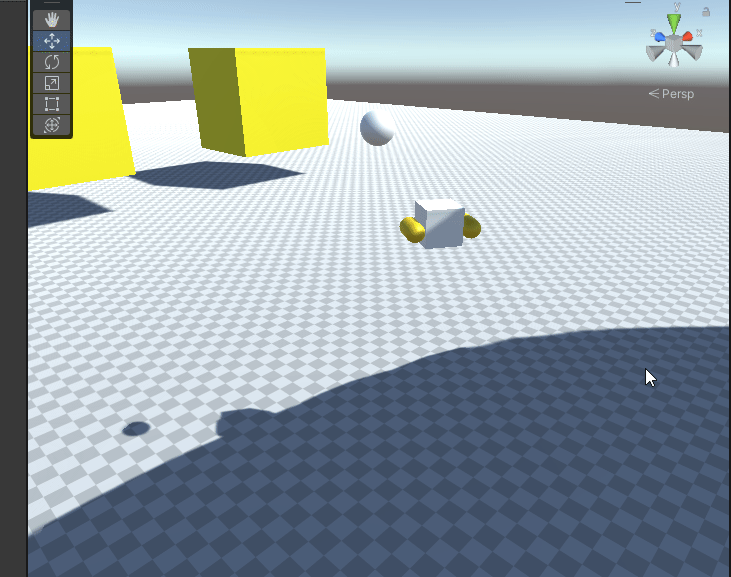
Unity基础课程之物理引擎6-关于物理材质的使用和理解
每个物体都有着不同的摩擦力。光滑的冰面摩擦力很小,而地毯表面的摩擦力则很大。另外每种材料也有着不同的弹性,橡皮表面的弹性大,硬质地面的弹性小。在Unity中这些现象都符合日常的理念。虽然从原理上讲,物体的摩擦力和弹性有着更…...

用c语言写一个剪刀石头布小游戏
用简单的生成随机数,来对电脑进行的选择。再用if else和swtich语句实现输出和输赢的判断 test.c: #define _CRT_SECURE_NO_WARNINGS#include "game.h"void menu() {printf("There can be choose for you,type:\n");printf("0 for rock\n&…...

【MySQL入门到精通-黑马程序员】MySQL基础篇-DCL
文章目录 前言一、DCL-介绍二、DCL-管理用户二、DCL-权限控制总结 前言 本专栏文章为观看黑马程序员《MySQL入门到精通》所做笔记,课程地址在这。如有侵权,立即删除。 一、DCL-介绍 DCL英文全称是Data Control Language(数据控制语言&#x…...
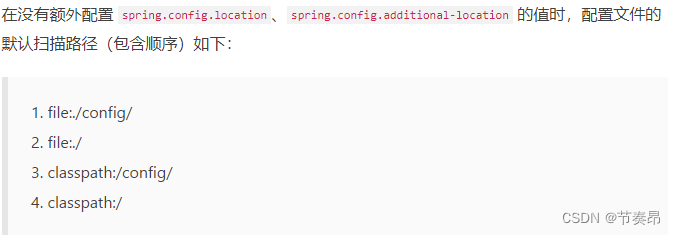
SpringBoot配置文件加载顺序
结论 参考文章: 链接: SpringBoot配置加载顺序 证明 下面是自己本地做的测试 每个配置里面是不同的端口号, 然后启动项目依次输入不同端口号看哪个能访问成功, 或者看启动日志的端口号是哪一个。 最终结果是 8204 —> 8205 —> 8202…...
github小记(一):清除github在add或者commit之后缓存区
github清除在add或者commit之后缓存区 前言1. 第一步之后想要撤销2. 第二步之后想要撤销a. 改变一下rrr.txt的内容b. 想提交本地文件的test文件夹c. 我后悔了突然不想提交了 前言 github自用 一般github上代码提交顺序: 第一步: git add . or git ad…...
【Debian系统】:安装debian系统之后,很多命令找不到,需要添加sudo之后才能使用,以下解决方法
项目场景: 问题描述 解决方案: 1.临时解决方案 2.永久解决方案 1.首先打开编辑: 2.打开之后最后一行添加代码: 3.最后运行一遍 .bashrc 4.已经可以了,可以试试reboot,重启一下机子 一点一滴才能成长 …...
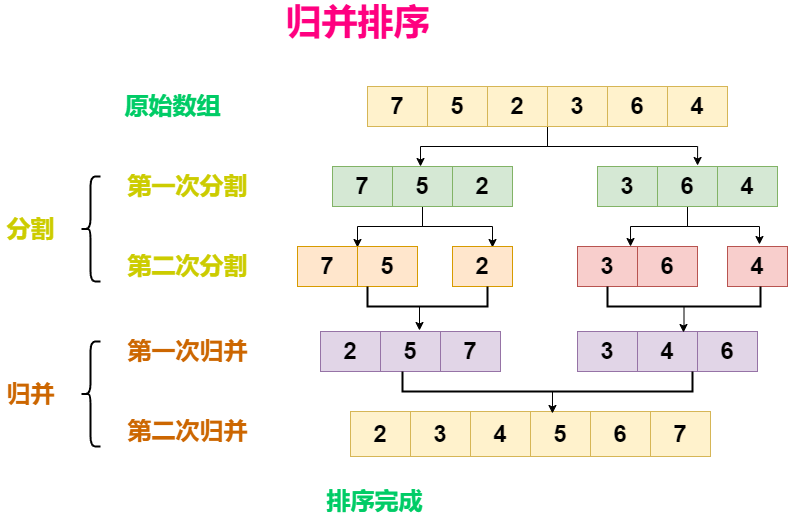
深入了解归并排序:原理、性能分析与 Java 实现
归并排序(Merge Sort)是一种高效且稳定的排序算法,其优雅的分治策略使它成为排序领域的一颗明珠。它的核心思想是将一个未排序的数组分割成两个子数组,然后递归地对子数组进行排序,最后将这些排好序的子数组合并起来。…...

docker stop了一个docker exec容器,要怎么再启动呢
docker restart <容器ID>...
【总结】kubernates 插件工具总结
在此记录工作中用到的关于 kubernates 的插件小工具,以防以后忘记 1、能显示 kubernates 所处上下文的插件 kube-ps1 github 地址: https://github.com/jonmosco/kube-ps1 效果 2、能方便切换 kubernates 上下文的插件 kubecm github 地址࿱…...

RK3588平台产测之ArmSoM-W3 DDR带宽监控
1. 简介 专栏总目录 ArmSoM团队在产品量产之前都会对产品做几次专业化的功能测试以及性能压力测试,以此来保证产品的质量以及稳定性 优秀的产品都要进行多次全方位的功能测试以及性能压力测试才能够经得起市场的检验 2. 环境介绍 硬件环境: ArmSoM-W…...
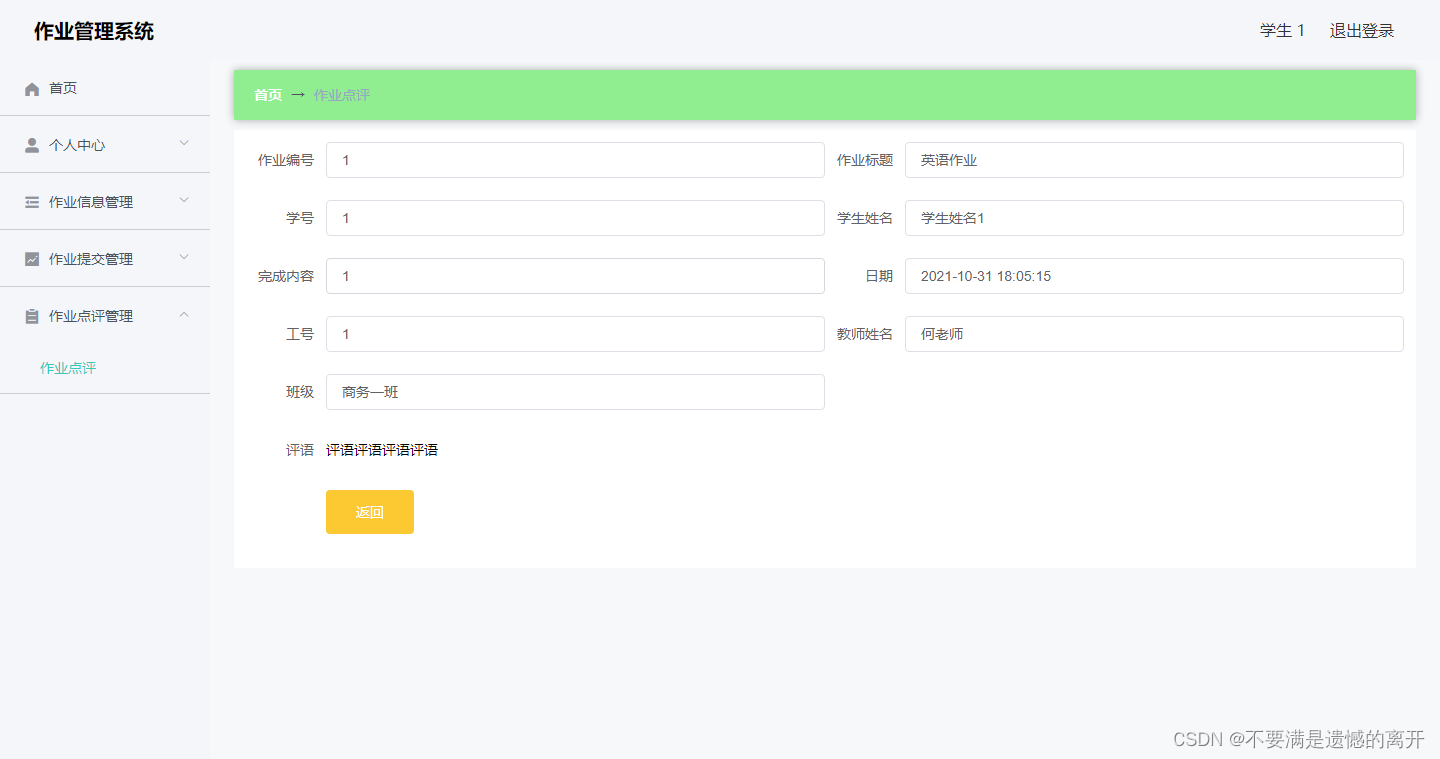
基于SpringBoot的作业管理系统设计与实现
目录 前言 一、技术栈 二、系统功能介绍 学生管理 教师管理 班级管理 作业管理 作业提交管理 作业点评管理 教师作业发布 学生作业提交 学生作业点评 三、核心代码 1、登录模块 2、文件上传模块 3、代码封装 前言 使用旧方法对作业管理信息进行系统化管理已经不再…...

TailwindCss Functions Directives
一般都写在一个 css 文件。 Directives tailwindlayerapplyconfig 【一般放在最后面,import 导入其他 css 文件后】 tailwind base; tailwind components; tailwind utilities;layer base {h1 {apply text-2xl;}h2 {apply text-xl;} }layer components {.btn-blu…...
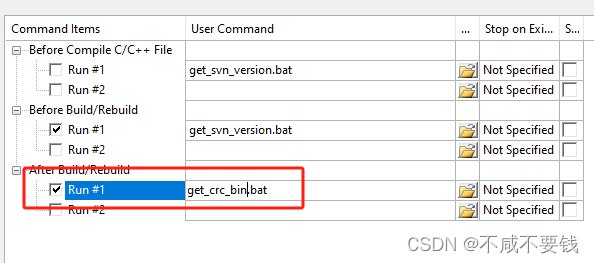
MDK自动生成带校验带SVN版本号的升级文件
MDK自动生成带校验带SVN版本号的升级文件 获取SVN版本信息 确保SVN安装了命令行工具,默认安装时不会安装命令行工具 编写一个模板头文件 svn_version.temp.h, 版本号格式为 1_0_0_SVN版本号 #ifndef __SVN_VERSION_H #define __SVN_VERSION_H#define SVN_REVISIO…...

如何打造一个网络框架模块对接服务器
一、了解网络框架的基本原理 在开始打造网络框架模块之前,首先需要了解网络框架的基本原理。网络框架是一个软件模块,用于处理网络通信的各种细节,包括数据传输、协议解析、错误处理等。常见的网络框架有HTTP、TCP/IP、WebSocket等。 对啦&…...
)
装饰器模式和 AOP 面向切片编程(设计模式与开发实践 P15)
文章目录 示例AOP 很多时候我们不希望一个类变得非常庞大,生来就包含很多职责。装饰器模式可以动态地给某个对象添加职责,而不会影响从这个类中派生的其他对象 为什么不用继承解决这个问题呢?如果用继承有可能会创造出数量庞大的子类&#x…...

Git迁移新仓库并保存历史提交记录
Git迁移新仓库并保存历史提交记录 第一步,从远程仓库克隆到本地 git clone https://gitee.com/oldxxx/oldxxx.git第二步,删除需要迁移的本地项目所关联的远程仓库地址 git remote remove origin第三步,关联新仓库的地址 git remote add o…...

MySql逗号分割的字段数据分解为多行
在 MySQL 中,你可以使用函数 REPLACE 和 SUBSTRING_INDEX 来将一行逗号分隔的数据分解为多行。 例如,假设你有一个表,其中包含一列 items,该列包含逗号分隔的字符串,如下所示: -------------------------…...
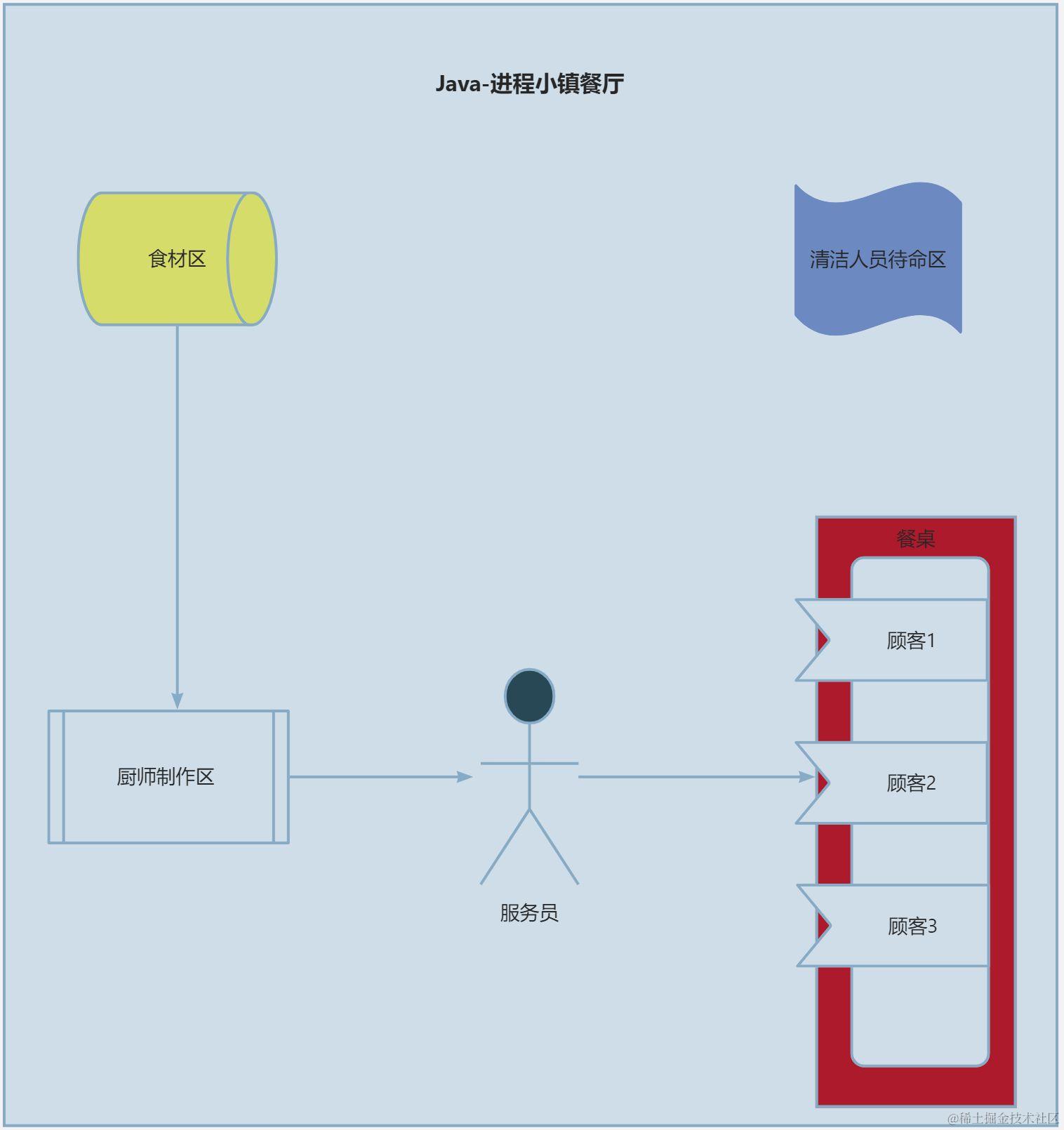
共生与共享:线程与进程的关系
🌍前言 在计算机科学和操作系统领域,线程(Thread)和进程(Process)是两个关键概念。它们之间存在密切的关系,但又有着明显的区别。本文将深入探讨线程和进程之间的关系,以及它们在并…...

uniapp app或微信小程序项目使用gite仓库中的图片
注意:以下不适用于浏览器 第一步:新建仓库并上传图片 第二步:设置开源 第三步:复制图片地址如: https://gitee.com/jiaomingyu/project-img/blob/master/xkmb/haibao/moban/BB_474x707_0_da.png 第四步࿱…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
