代码随想录算法训练营day41 | 动态规划 01背包问题基础 01背包问题之滚动数组
01背包问题基础
问题描述
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
举个栗子
背包最大重量为4。
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
二维dp数组01背包
动归五部曲
1.确定dp数组以及下标的含义
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
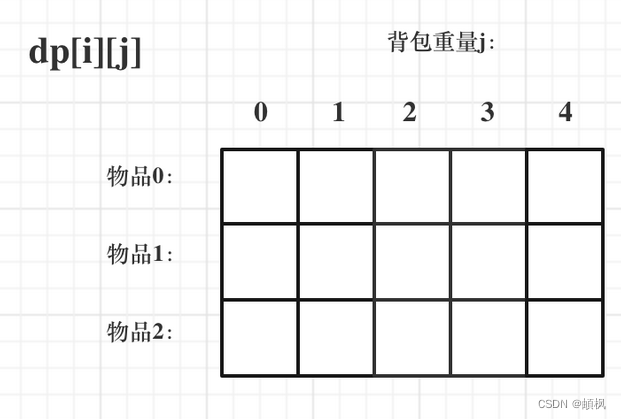
2.确定递推公式
可以有两个方向推出来dp[i][j],
- 不放物品i:由
dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以被背包内的价值依然和前面相同。) - 放物品i:由
dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]]为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i](物品i的价值),就是背包放物品i得到的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
3.dp数组如何初始化
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
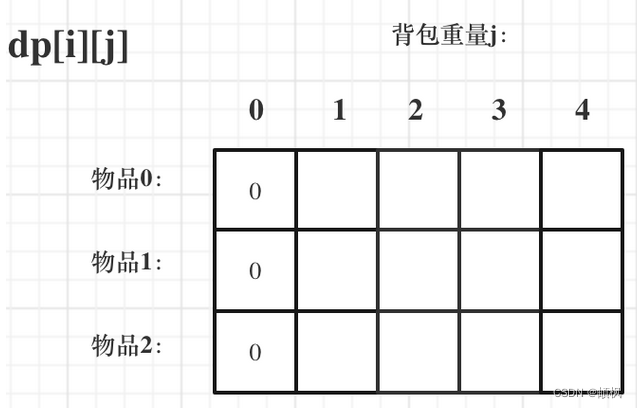
其次是其他情况。状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
代码初始化如下:
for (int j = 0 ; j < weight[0]; j++) { // 当然这一步,如果把dp数组预先初始化为0了,这一步就可以省略,但很多同学应该没有想清楚这一点。dp[0][j] = 0;
}
// 正序遍历
for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];
}
此时dp数组初始化情况如图所示:
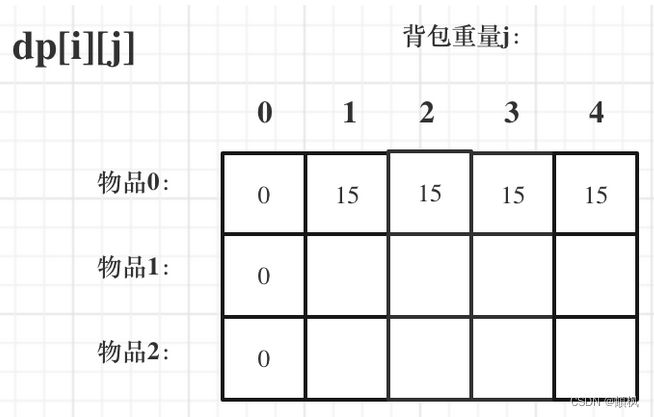
dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
其实从递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出dp[i][j] 是由左上方数值推导出来了,那么 其他下标初始为什么数值都可以,因为都会被覆盖。
所以为了方便,可以初始化为0。

最后初始化代码如下:
// 初始化 dp
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];
}
4.确定遍历顺序
先遍历 物品还是先遍历背包重量呢?其实都可以,但是先遍历物品更好理解。
那么我先给出先遍历物品,然后遍历背包重量的代码。
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品for(int j = 0; j <= bagweight; j++) { // 遍历背包容量if (j < weight[i]) dp[i][j] = dp[i - 1][j]; else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}
}
5.举例推导dp数组
对应的dp数组的数值,如图:
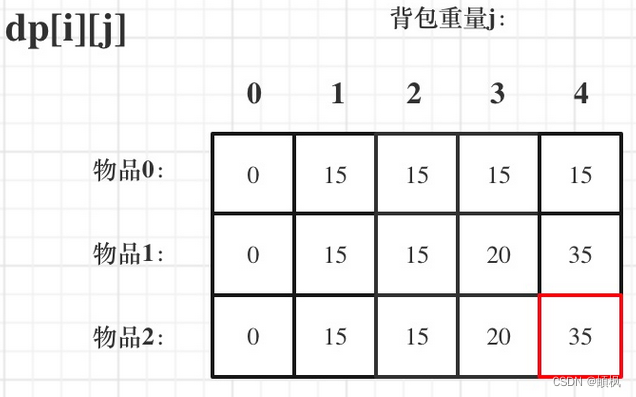
void test_2_wei_bag_problem1() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagweight = 4;// 二维数组vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));// 初始化for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];}// weight数组的大小 就是物品个数for(int i = 1; i < weight.size(); i++) { // 遍历物品for(int j = 0; j <= bagweight; j++) { // 遍历背包容量if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}cout << dp[weight.size() - 1][bagweight] << endl;
}int main() {test_2_wei_bag_problem1();
}01背包问题之滚动数组(二维转化成一维)
动规五部曲分析如下:
1.确定dp数组的定义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
2.一维dp数组的递推公式
dp[j]为 容量为j的背包所背的最大价值,那么如何推导dp[j]呢?
dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])
此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值,
所以递归公式为:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
可以看出相对于二维dp数组的写法,就是把dp[i][j]中i的维度去掉了。
3.一维dp数组如何初始化
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?
看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
那么我假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0就可以了。
4.一维dp数组遍历顺序
代码如下:
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
这里大家发现和二维dp的写法中,遍历背包的顺序是不一样的!
二维dp遍历的时候,背包容量是从小到大,而一维dp遍历的时候,背包是从大到小。
为什么呢?
倒序遍历是为了保证物品i只被放入一次!。但如果一旦正序遍历了,那么物品0就会被重复加入多次!
举一个例子:物品0的重量weight[0] = 1,价值value[0] = 15
如果正序遍历
dp[1] = dp[1 - weight[0]] + value[0] = 15dp[2] = dp[2 - weight[0]] + value[0] = 30
此时dp[2]就已经是30了,意味着物品0,被放入了两次,所以不能正序遍历。
为什么倒序遍历,就可以保证物品只放入一次呢?
倒序就是先算dp[2]
dp[2] = dp[2 - weight[0]] + value[0] = 15 (dp数组已经都初始化为0)dp[1] = dp[1 - weight[0]] + value[0] = 15
所以从后往前循环,每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
那么问题又来了,为什么二维dp数组历的时候不用倒序呢?
因为对于二维dp,dp[i][j]都是通过上一层即dp[i - 1][j]计算而来,本层的dp[i][j]并不会被覆盖!
再来看看两个嵌套for循环的顺序,代码中是先遍历物品嵌套遍历背包容量,那可不可以先遍历背包容量嵌套遍历物品呢?
不可以!
因为一维dp的写法,背包容量一定是要倒序遍历(原因上面已经讲了),如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品,即:背包里只放入了一个物品。
倒序遍历的原因是,本质上还是一个对二维数组的遍历,并且右下角的值依赖上一层左上角的值,因此需要保证左边的值仍然是上一层的,从右向左覆盖。
所以一维dp数组的背包在遍历顺序上和二维其实是有很大差异的!,这一点大家一定要注意。
5.举例推导dp数组
一维dp,分别用物品0,物品1,物品2 来遍历背包,最终得到结果如下:
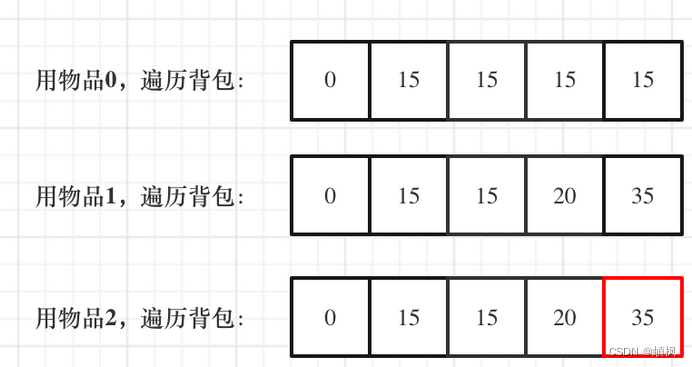
void test_1_wei_bag_problem() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagWeight = 4;// 初始化vector<int> dp(bagWeight + 1, 0);for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bagWeight] << endl;
}int main() {test_1_wei_bag_problem();
}
相关文章:

代码随想录算法训练营day41 | 动态规划 01背包问题基础 01背包问题之滚动数组
01背包问题基础 问题描述 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 举个栗子 背包最大重量为4。 物品为: 重量价值…...
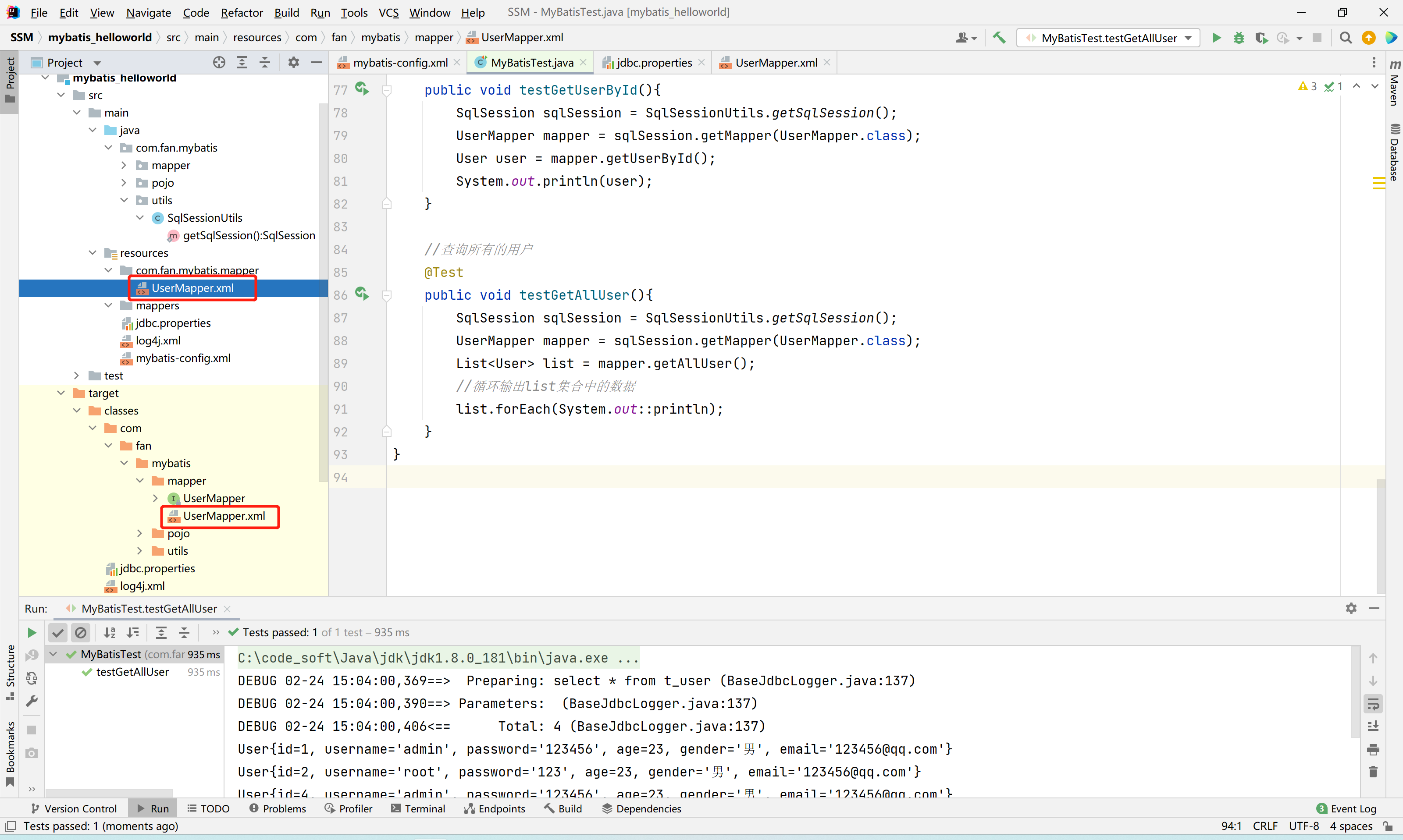
MyBatis学习笔记(三) —— MyBatis核心配置文件详解
3、核心配置文件详解 id是唯一标识,不能重复,但是在真正开发过程中,不可能一个项目中同时使用两个环境,肯定会使用其中的某一个,这时候它的default就比较重要了。 default是设置我们当前使用的默认环境的id <?x…...
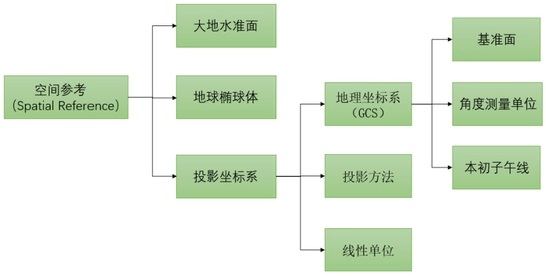
使用GDAL进行坐标转换
1、地理坐标系与投影坐标系空间参考中主要包含大地水准面、地球椭球体、投影坐标系等几部分内容。地图投影就是把地球表面的任意点,利用一定数学法则,转换到地图平面上的理论和方法,一般有两种坐标系来进行表示,分别是地理坐标系和…...

日常编程中和日期相关的代码和bug
本文主要是Java中和日期时间相隔的几个常用代码函数代码,做了总结,希望在日常编码中,可以帮到大家。 1.计算闰年 记住一个短语,“四年一润,百年不闰,四百再润”,不管换啥语言,相信…...

ATT与Intel汇编语法区别
寄存器、变量(常量)与立即数 在Intel汇编中,无论是寄存器、变量(常量)还是立即数,都是直接使用的,例如下列例子中分别加载一个变量(常量)与立即数到寄存器中:…...

Spring Cloud Alibaba全家桶(一)——Spring Cloud Alibaba介绍
前言 本文为 Spring Cloud Alibaba介绍 相关知识,下边将对微服务介绍(包括:系统架构演变、微服务架构介绍、常见微服务架构),Spring Cloud Alibaba介绍(包括:Spring Cloud Alibaba 的定位、Spri…...
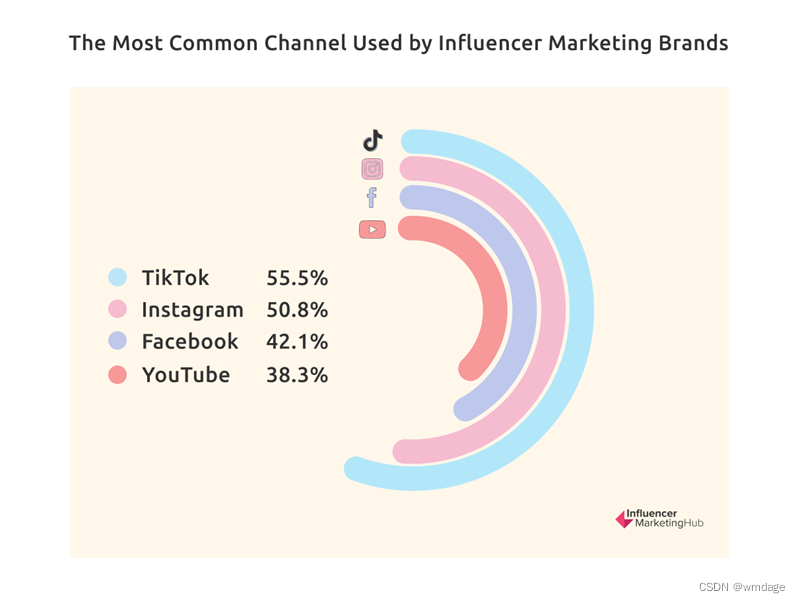
2023年网红营销10大趋势解读:品牌出海必看
前不久influencermarketinghub发布了《2023年影响者营销基准报告》,报告总结了3500多家营销机构、品牌和其他相关专业人士对当前网红营销现状的看法,以及预测了未来网红营销的一个发展趋势。本期Nox聚星就带领大家详细解读关于2023年网红营销的10大趋势。…...

Java学习笔记 --- 正则表达式
一、体验正则表达式 package com.javase.regexp;import java.util.regex.Matcher; import java.util.regex.Pattern;/*** 体验正则表达式,给文本处理带来哪些便利*/ public class Regexp_ {public static void main(String[] args) {//假设,编写了爬虫&…...

【基础算法】字符串哈希
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

unity 多个模型或物体无限循环拖拽 类似无限列表循环
using System.Collections; using System.Collections.Generic; using UnityEngine; public class ModelAnimal : MonoBehaviour { //需滑动的物体 public GameObject m_objA; //音乐 public GameObject m_objB; //电话 public GameObject m_objC; //导航 public GameObject m…...

GroupDocs.Merger for Java
GroupDocs.Merger for Java GroupDocs.Merger for Java是一个文档操作API,可帮助您合并、拆分、交换或删除文档页面。API通过启用或禁用密码提供保护,并允许开发人员加入PDF、Microsoft Word、Excel和Powerpoint文档。 支持的文件格式 Microsoft Office格…...
04--WXML
1、什么是WXML什么是Wxml呢?我们首先要介绍一下Html,Html的全称为HyperTextMarkup Language,翻译过来就是超文本标记语言,这种语言目前已经普遍用于前端开发,而wxml正是从html演变而来,它基于微信这个平台&…...

一篇五分生信临床模型预测文章代码复现——FIgure 9.列线图构建,ROC分析,DCA分析 (五)
之前讲过临床模型预测的专栏,但那只是基础版本,下面我们以自噬相关基因为例子,模仿一篇五分文章,将图和代码复现出来,学会本专栏课程,可以具备发一篇五分左右文章的水平: 本专栏目录如下: Figure 1:差异表达基因及预后基因筛选(图片仅供参考) Figure 2. 生存分析,…...
《狂飙》)
每月一书(202302)《狂飙》
文章目录剧情内容观看收获正菜很硬配菜很足食物还有喻义又到了每月一书的时间,本月没有阅读书籍,不过看了一部叫《狂飙》的电视剧,因为该电视剧热度高,所以我也凑个热闹。下面分享一下我看完后的体会。 剧情内容 这是一部扫黑和…...

wsl2 docker 安装
一. 更换镜像源 备份默认源: cp /etc/apt/sources.list /etc/apt/sourses.list.bak 编辑文件: vim /etc/apt/sources.list 删除原有内容并替换为: # 默认注释了源码镜像以提高 apt update 速度,如有需要可自行取消注释 deb …...
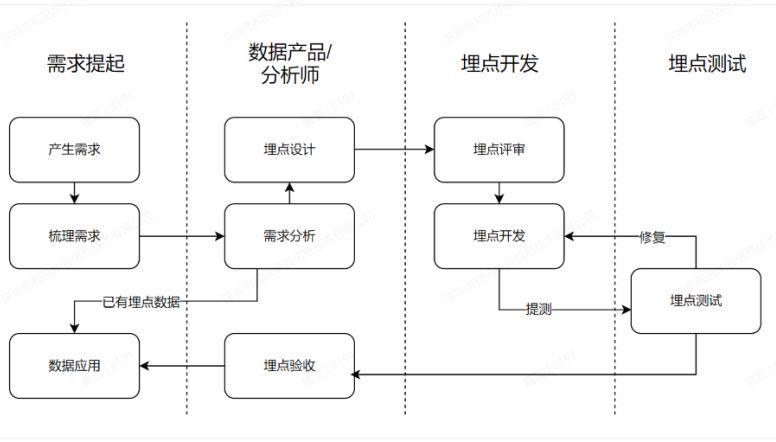
极光笔记 | 埋点体系建设与实施方法论
PART 01 前 言随着网络技术的发展,从粗犷型到精细化运营型,再到现在的数字化运营,数据变得越来越细分和重要,不仅可以进行策略调整,还可以实现自动化的精细化运营。而数据价值的起点就是埋点,只有合理地埋点…...

SpringMVC中的各注解类理解
目录 一、概念 二、springmvc注解详解 (一)控制层注解 1.Controller 2.RequestMapping 3.ResponseBody (二)配置类(bean类)注解 4.configuration 5.Bean 一、概念 在学习springmvc的时候&#x…...

DNF搭建服务器服务端搭建教程
DNF搭建服务器服务端搭建教程 我是艾西,今天给大家分享下怎么样自己搭建一个DNF。 前阵子体验了下其他GM搭建的服,那么对于自己搭建的好处在于出道即巅峰! 想要什么武器就是一串代码命令的事情。 下面我跟大家说一下需要准备那些东西&#x…...

【论文简述】Learning Optical Flow with Adaptive Graph Reasoning(AAAI 2022)
一、论文简述 1. 第一作者:Haofei Xu 2. 发表年份:2022 3. 发表期刊:AAAI 4. 关键词:光流、图神经网络、自适应 5. 探索动机:现有光流估计方法主要解决基于特征相似性的匹配问题,少有工作研究如何显式…...
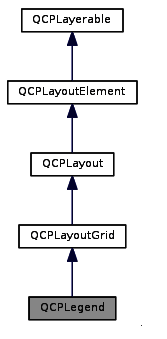
qt QCustomPlot学习
QCustomPlot 是一个基于Qt的画图和数据可视化C控件。QCustomPlot 致力于提供美观的界面,高质量的2D画图、图画和图表,同时为实时数据可视化应用提供良好的解决方案。 该绘图库专注于制作美观、出版物质量高的2D绘图、图形和图表,并为实时可视…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...
