Leetcode.1801 积压订单中的订单总数
题目链接
Leetcode.1801 积压订单中的订单总数 Rating : 1711
题目描述
给你一个二维整数数组 orders,其中每个 orders[i] = [pricei, amounti, orderTypei]表示有 amounti笔类型为 orderTypei、价格为 pricei的订单。
订单类型 orderTypei 可以分为两种:
0表示这是一批采购订单buy1表示这是一批销售订单sell
注意,orders[i]表示一批共计 amounti笔的独立订单,这些订单的价格和类型相同。对于所有有效的 i,由 orders[i]表示的所有订单提交时间均早于 orders[i+1]表示的所有订单。
存在由未执行订单组成的 积压订单 。积压订单最初是空的。提交订单时,会发生以下情况:
- 如果该订单是一笔采购订单
buy,则可以查看积压订单中价格 最低 的销售订单sell。如果该销售订单sell的价格 低于或等于 当前采购订单buy的价格,则匹配并执行这两笔订单,并将销售订单sell从积压订单中删除。否则,采购订单buy将会添加到积压订单中。 - 反之亦然,如果该订单是一笔销售订单
sell,则可以查看积压订单中价格 最高 的采购订单buy。如果该采购订单buy的价格 高于或等于 当前销售订单sell的价格,则匹配并执行这两笔订单,并将采购订单buy从积压订单中删除。否则,销售订单sell将会添加到积压订单中。
输入所有订单后,返回积压订单中的 订单总数 。由于数字可能很大,所以需要返回对 109+710^9 + 7109+7 取余的结果。
示例 1:
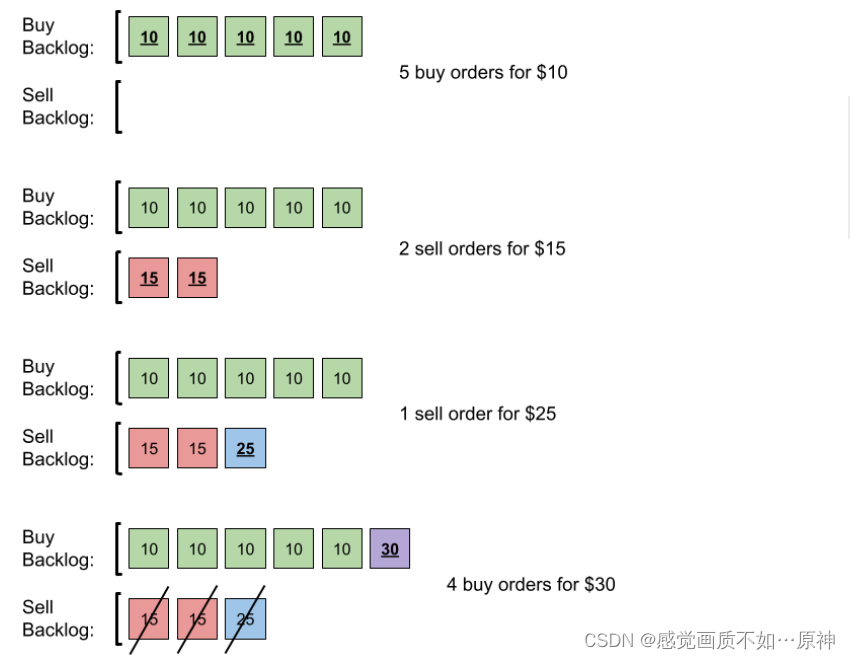
输入:orders = [[10,5,0],[15,2,1],[25,1,1],[30,4,0]]
输出:6
解释:输入订单后会发生下述情况:
提交 5 笔采购订单,价格为 10 。没有销售订单,所以这 5 笔订单添加到积压订单中。
提交 2 笔销售订单,价格为 15 。没有采购订单的价格大于或等于 15 ,所以这 2 笔订单添加到积压订单中。
提交 1 笔销售订单,价格为 25 。没有采购订单的价格大于或等于 25 ,所以这 1 笔订单添加到积压订单中。
提交 4 笔采购订单,价格为 30 。前 2 笔采购订单与价格最低(价格为 15)的 2 笔销售订单匹配,从积压订单中删除这 2 笔销售订单。第 3 笔采购订单与价格最低的 1 笔销售订单匹配,销售订单价格为 25 ,从积压订单中删除这 1
笔销售订单。积压订单中不存在更多销售订单,所以第 4 笔采购订单需要添加到积压订单中。 最终,积压订单中有 5 笔价格为 10
的采购订单,和 1 笔价格为 30 的采购订单。所以积压订单中的订单总数为 6 。
示例 2:
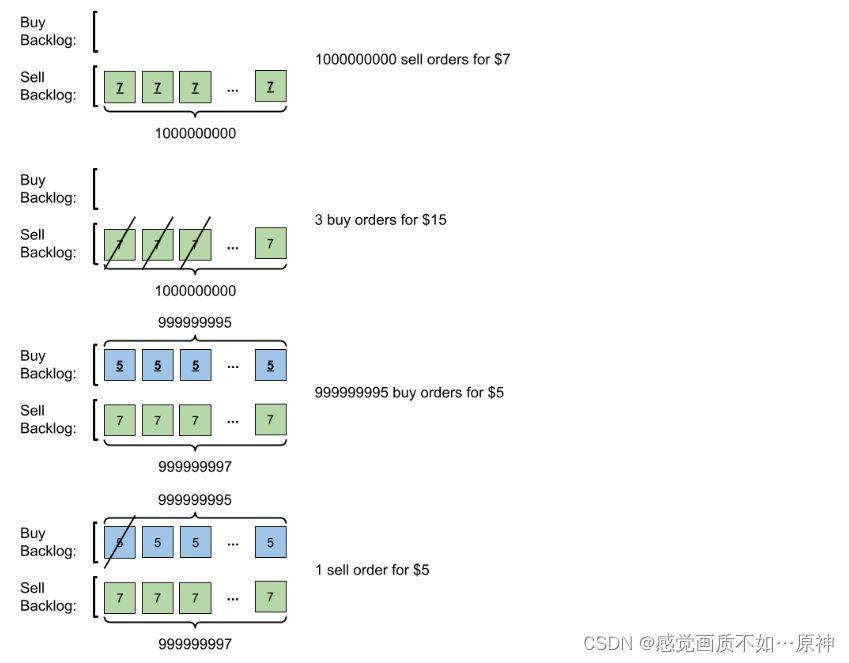
输入:orders = [[7,1000000000,1],[15,3,0],[5,999999995,0],[5,1,1]]
输出:999999984
解释:输入订单后会发生下述情况:
提交 109 笔销售订单,价格为 7 。没有采购订单,所以这 109 笔订单添加到积压订单中。
提交 3 笔采购订单,价格为 15 。这些采购订单与价格最低(价格为 7 )的 3 笔销售订单匹配,从积压订单中删除这 3 笔销售订单。
提交 999999995 笔采购订单,价格为 5 。销售订单的最低价为 7 ,所以这 999999995 笔订单添加到积压订单中。
提交 1 笔销售订单,价格为 5 。这笔销售订单与价格最高(价格为 5 )的 1 笔采购订单匹配,从积压订单中删除这 1 笔采购订单。 最终,积压订单中有 (1000000000-3) 笔价格为 7 的销售订单,和 (999999995-1) 笔价格为 5
的采购订单。所以积压订单中的订单总数为 1999999991 ,等于 999999984 % (10^9 + 7) 。
提示:
- 1<=orders.length<=1051 <= orders.length <= 10^51<=orders.length<=105
- orders[i].length==3orders[i].length == 3orders[i].length==3
- 1<=pricei,amounti<=1091 <= pricei, amounti <= 10^91<=pricei,amounti<=109
orderTypei为0或1
分析:
我们用两个 堆 来模拟这个过程。堆里面存的是 (price,amount)这样的二元组。
对于 buy订单,用一个 大顶堆 来存储,因为每次要选择最大的 buy订单。
对于 sell订单,用一个 小顶堆 来存储,因为每次要选择最小的 sell订单。
直接模拟这个过程即可。
时间复杂度:O(nlogn)O(nlogn)O(nlogn)
代码:
const int MOD = 1e9+7;
using PII = pair<int,int>;
class Solution {
public:int getNumberOfBacklogOrders(vector<vector<int>>& orders) {priority_queue<PII,vector<PII>,greater<PII>> sell;priority_queue<PII> buy;for(auto o:orders){int price = o[0] , amount = o[1] , type = o[2];//buyif(type == 0){while(!sell.empty() && sell.top().first <= price){if(amount == 0) break;auto [p,cnt] = sell.top();sell.pop();if(cnt <= amount) amount -= cnt;else{cnt -= amount;amount = 0;sell.push({p,cnt});}}if(amount > 0) buy.push({price,amount}); }//sellelse{while(!buy.empty() && buy.top().first >= price){if(amount == 0) break;auto [p,cnt] = buy.top();buy.pop();if(cnt <= amount) amount -= cnt;else{cnt -= amount;amount = 0;buy.push({p,cnt});}}if(amount > 0) sell.push({price,amount});}}int ans = 0;while(!sell.empty()){auto[_,cnt] = sell.top();ans = (ans + cnt) % MOD;sell.pop();}while(!buy.empty()){auto[_,cnt] = buy.top();ans = (ans + cnt) % MOD;buy.pop();} return ans; }
};
相关文章:

Leetcode.1801 积压订单中的订单总数
题目链接 Leetcode.1801 积压订单中的订单总数 Rating : 1711 题目描述 给你一个二维整数数组 orders,其中每个 orders[i] [pricei, amounti, orderTypei]表示有 amounti笔类型为 orderTypei、价格为 pricei的订单。 订单类型 orderTypei 可以分为两种…...

红帽Linux技术-cp命令
cp是一个复制文件或者目录的命令,其作用是将一个或多个文件或目录从源位置复制到目标位置。 格式:cp [选项] 源文件或目录 目标文件或目录 常用选项: -r:复制目录及其子目录下的所有文件和目录; -p:保留…...
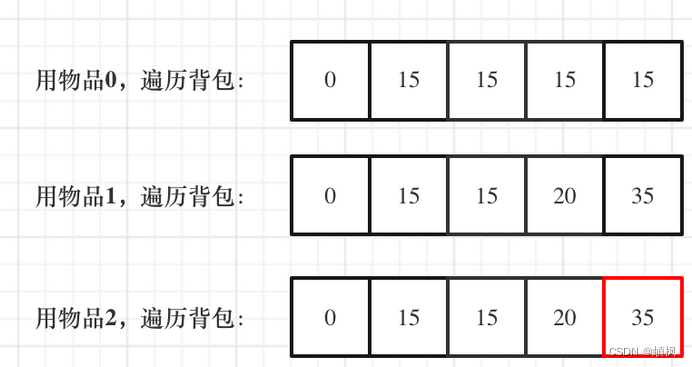
代码随想录算法训练营day41 | 动态规划 01背包问题基础 01背包问题之滚动数组
01背包问题基础 问题描述 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 举个栗子 背包最大重量为4。 物品为: 重量价值…...
MyBatis学习笔记(三) —— MyBatis核心配置文件详解
3、核心配置文件详解 id是唯一标识,不能重复,但是在真正开发过程中,不可能一个项目中同时使用两个环境,肯定会使用其中的某一个,这时候它的default就比较重要了。 default是设置我们当前使用的默认环境的id <?x…...
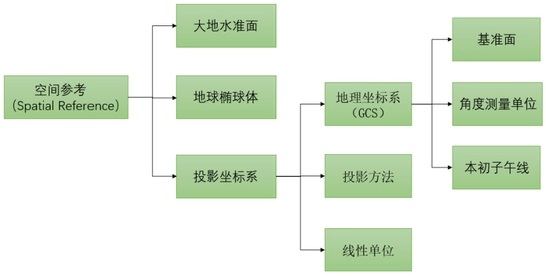
使用GDAL进行坐标转换
1、地理坐标系与投影坐标系空间参考中主要包含大地水准面、地球椭球体、投影坐标系等几部分内容。地图投影就是把地球表面的任意点,利用一定数学法则,转换到地图平面上的理论和方法,一般有两种坐标系来进行表示,分别是地理坐标系和…...

日常编程中和日期相关的代码和bug
本文主要是Java中和日期时间相隔的几个常用代码函数代码,做了总结,希望在日常编码中,可以帮到大家。 1.计算闰年 记住一个短语,“四年一润,百年不闰,四百再润”,不管换啥语言,相信…...

ATT与Intel汇编语法区别
寄存器、变量(常量)与立即数 在Intel汇编中,无论是寄存器、变量(常量)还是立即数,都是直接使用的,例如下列例子中分别加载一个变量(常量)与立即数到寄存器中:…...

Spring Cloud Alibaba全家桶(一)——Spring Cloud Alibaba介绍
前言 本文为 Spring Cloud Alibaba介绍 相关知识,下边将对微服务介绍(包括:系统架构演变、微服务架构介绍、常见微服务架构),Spring Cloud Alibaba介绍(包括:Spring Cloud Alibaba 的定位、Spri…...
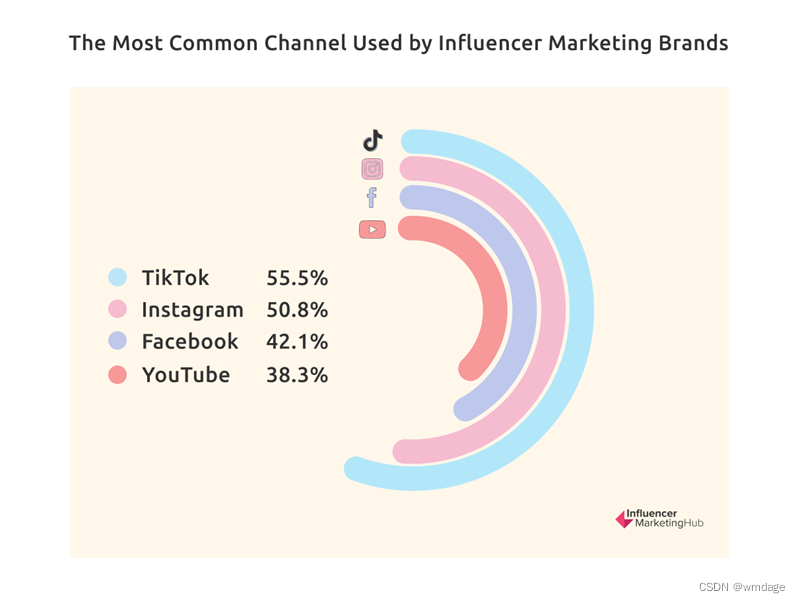
2023年网红营销10大趋势解读:品牌出海必看
前不久influencermarketinghub发布了《2023年影响者营销基准报告》,报告总结了3500多家营销机构、品牌和其他相关专业人士对当前网红营销现状的看法,以及预测了未来网红营销的一个发展趋势。本期Nox聚星就带领大家详细解读关于2023年网红营销的10大趋势。…...

Java学习笔记 --- 正则表达式
一、体验正则表达式 package com.javase.regexp;import java.util.regex.Matcher; import java.util.regex.Pattern;/*** 体验正则表达式,给文本处理带来哪些便利*/ public class Regexp_ {public static void main(String[] args) {//假设,编写了爬虫&…...

【基础算法】字符串哈希
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

unity 多个模型或物体无限循环拖拽 类似无限列表循环
using System.Collections; using System.Collections.Generic; using UnityEngine; public class ModelAnimal : MonoBehaviour { //需滑动的物体 public GameObject m_objA; //音乐 public GameObject m_objB; //电话 public GameObject m_objC; //导航 public GameObject m…...

GroupDocs.Merger for Java
GroupDocs.Merger for Java GroupDocs.Merger for Java是一个文档操作API,可帮助您合并、拆分、交换或删除文档页面。API通过启用或禁用密码提供保护,并允许开发人员加入PDF、Microsoft Word、Excel和Powerpoint文档。 支持的文件格式 Microsoft Office格…...
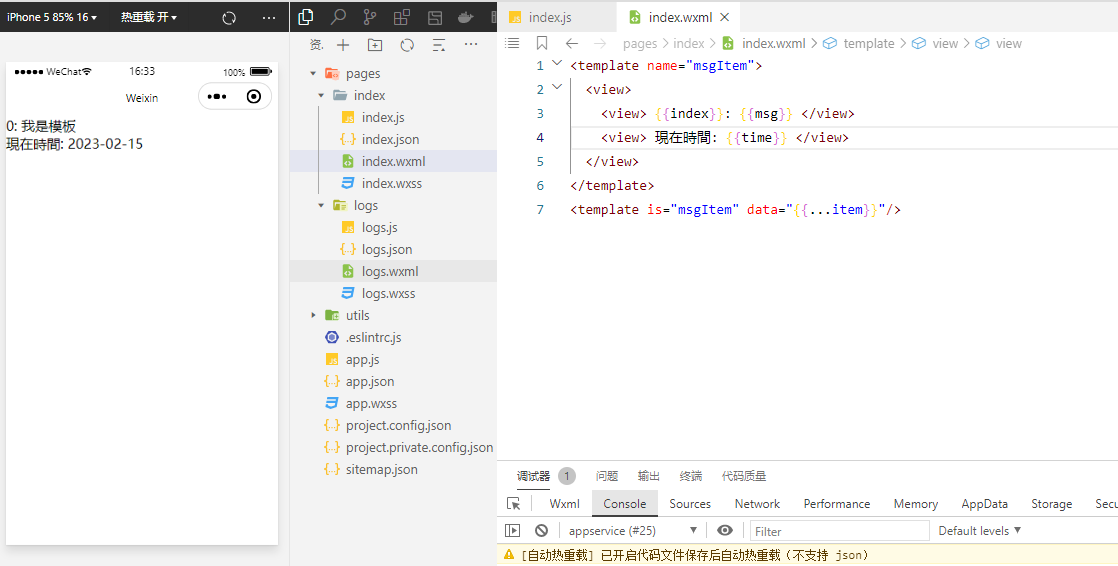
04--WXML
1、什么是WXML什么是Wxml呢?我们首先要介绍一下Html,Html的全称为HyperTextMarkup Language,翻译过来就是超文本标记语言,这种语言目前已经普遍用于前端开发,而wxml正是从html演变而来,它基于微信这个平台&…...

一篇五分生信临床模型预测文章代码复现——FIgure 9.列线图构建,ROC分析,DCA分析 (五)
之前讲过临床模型预测的专栏,但那只是基础版本,下面我们以自噬相关基因为例子,模仿一篇五分文章,将图和代码复现出来,学会本专栏课程,可以具备发一篇五分左右文章的水平: 本专栏目录如下: Figure 1:差异表达基因及预后基因筛选(图片仅供参考) Figure 2. 生存分析,…...
《狂飙》)
每月一书(202302)《狂飙》
文章目录剧情内容观看收获正菜很硬配菜很足食物还有喻义又到了每月一书的时间,本月没有阅读书籍,不过看了一部叫《狂飙》的电视剧,因为该电视剧热度高,所以我也凑个热闹。下面分享一下我看完后的体会。 剧情内容 这是一部扫黑和…...

wsl2 docker 安装
一. 更换镜像源 备份默认源: cp /etc/apt/sources.list /etc/apt/sourses.list.bak 编辑文件: vim /etc/apt/sources.list 删除原有内容并替换为: # 默认注释了源码镜像以提高 apt update 速度,如有需要可自行取消注释 deb …...
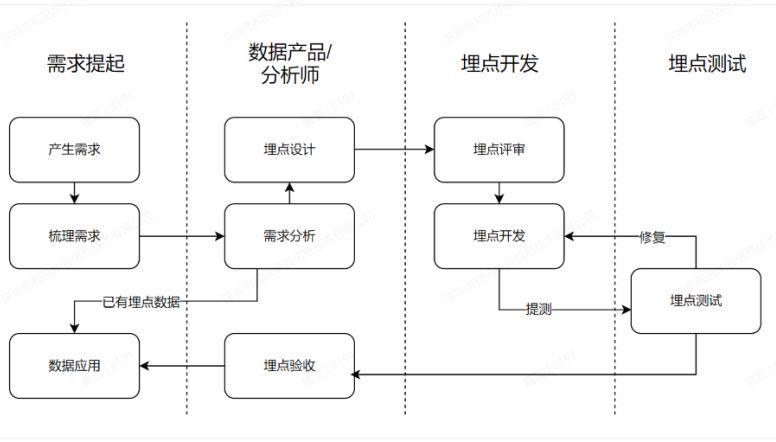
极光笔记 | 埋点体系建设与实施方法论
PART 01 前 言随着网络技术的发展,从粗犷型到精细化运营型,再到现在的数字化运营,数据变得越来越细分和重要,不仅可以进行策略调整,还可以实现自动化的精细化运营。而数据价值的起点就是埋点,只有合理地埋点…...

SpringMVC中的各注解类理解
目录 一、概念 二、springmvc注解详解 (一)控制层注解 1.Controller 2.RequestMapping 3.ResponseBody (二)配置类(bean类)注解 4.configuration 5.Bean 一、概念 在学习springmvc的时候&#x…...

DNF搭建服务器服务端搭建教程
DNF搭建服务器服务端搭建教程 我是艾西,今天给大家分享下怎么样自己搭建一个DNF。 前阵子体验了下其他GM搭建的服,那么对于自己搭建的好处在于出道即巅峰! 想要什么武器就是一串代码命令的事情。 下面我跟大家说一下需要准备那些东西&#x…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...
