《3D 数学基础》几何检测-相交性检测
目录
1. 2D直线相交
2. 3D射线相交点
3. 射线和平面的交点
4. 3个平面的交点
5. 射线和圆或者球交点
6. 两个圆或者球是否相交
7. 球和平面的相交性检测
8. 射线和AABB的相交性(13.17)
9. 射线和三角形的相交性(13.16)
10. 两个AABB的相交性(也叫碰撞检测)
1. 2D直线相交

直线方程,求交点(x,y)。
(1)分母不为0,则有唯一一个解;
(2)分母为0,则平行。
2. 3D射线相交点
其实是求t,知道相交点的t值,利用射线公式就知道相交点坐标。

3. 射线和平面的交点
把射线方程代入平面方程中,求出自变量t即可。

4. 3个平面的交点

交点p,以向量表示(x,y,z)。
5. 射线和圆或者球交点
求射线参数t.
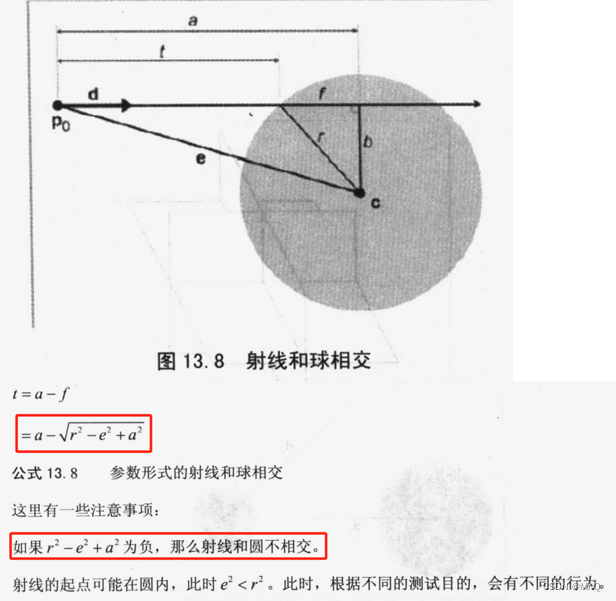
其中a是将e投影到d,这个向量的长度是a, 投影公式是a=e·d; e=c-p0
6. 两个圆或者球是否相交
(1)静态相交性
圆心距离d < r1+r2时,不相交;为避免求d是开方,一般使用d^2 < (r1+r2)^2.
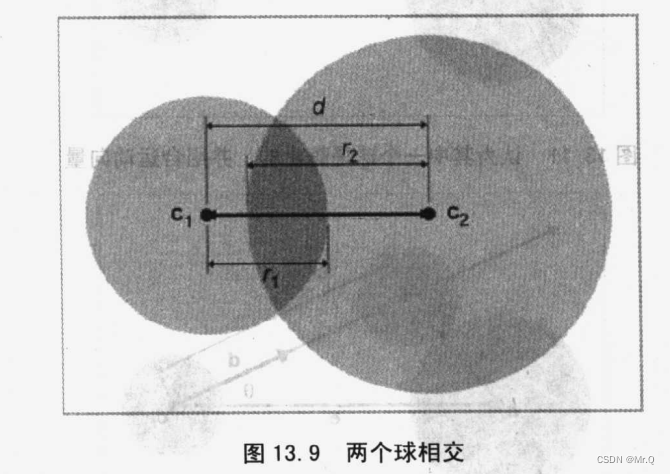
(2)动态相交性
两个球在分别移动d1和d2的过程中是否会相交的,如下,d1和d2是移动向量
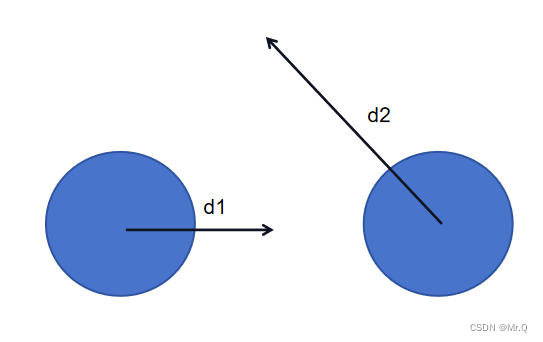
因为移动是相对的,所以可以将左边的球设置为静止的,右边的移动方向就变成d,如下。

以c_m为原点,d为移动的方向向量,t为自变量的射线p(t) = c_m + td。变成了求射线自变量t值。
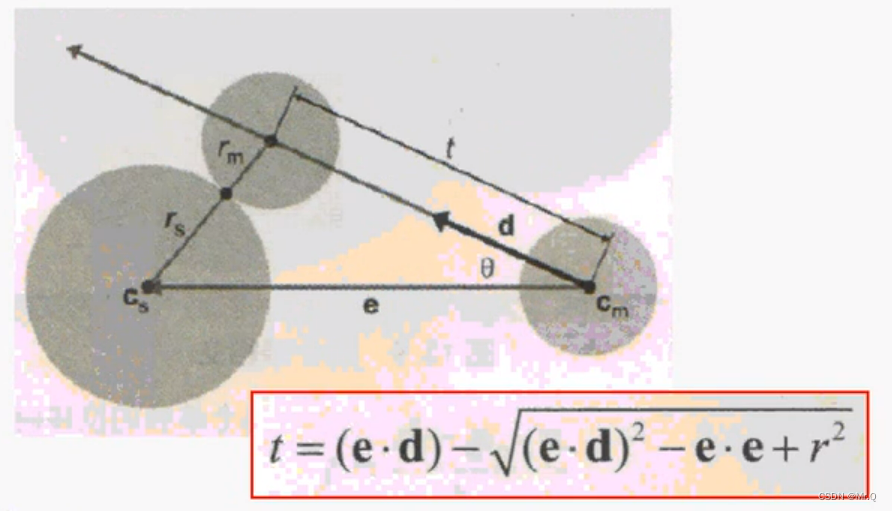
其r=r_s + r_m。

7. 球和平面的相交性检测
(1)静态相交性
平面公式: p·n = d,n是单位向量; 球:由半径r和球心初始位置c表示。
计算球心到平面的距离:dis = n·c - d
- dis >= r,球完全在平面的前面;
- dis<= -r,在平面的背面;
- 否则,球横跨平面(即相交)。
(2)动态相交性
如果两个都在运动,则换成一个静止,一个做相对运动(如上面的两个圆或者球是否相交)
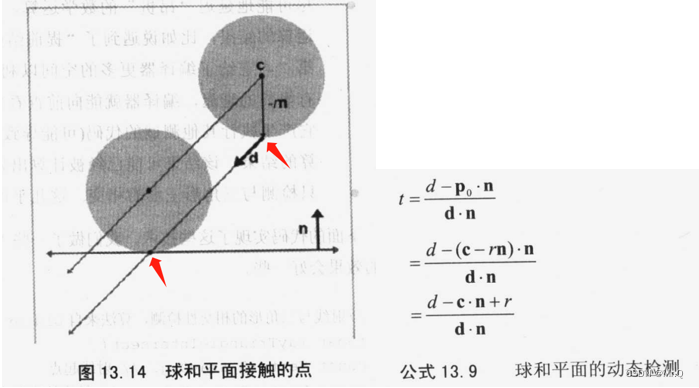
单位向量d指明方向,使用射线方程c+td记录球心运动轨迹。平面公式是p·n=d,n是单位向量。球心运动t时,会与平面相交。
交点是c - r n
后面几个较为复杂
8. 射线和AABB的相交性(13.17)
附录有实现
9. 射线和三角形的相交性(13.16)
书上有实现。
10. 两个AABB的相交性(也叫碰撞检测)
静止相交性检测是简单的,需要在每个维度上单独检测他们的相交性即可。

动态的很复杂。且实际情况中,很少有轴对齐于同一个坐标系空间中的。
参考:37.几何检测_哔哩哔哩_bilibili
相关文章:

《3D 数学基础》几何检测-相交性检测
目录 1. 2D直线相交 2. 3D射线相交点 3. 射线和平面的交点 4. 3个平面的交点 5. 射线和圆或者球交点 6. 两个圆或者球是否相交 7. 球和平面的相交性检测 8. 射线和AABB的相交性(13.17) 9. 射线和三角形的相交性(13.16) …...

文字与视频结合效果
效果展示 CSS 知识点 mix-blend-mode 属性的运用 实现整体页面布局 <section class"sec"><video autoplay muted loop><source src"./video.mp4" type"video/mp4" /></video><h2>Run</h2><!-- 用于切…...

大数据Doris(九):配置BE步骤
文章目录 配置BE步骤 一、配置be节点...

BuyVM 纽约 VPS 测评
description: 发布于 2023-07-05 BuyVM 纽约 VPS 测评 产品链接:https://my.frantech.ca/cart.php?gid38 G口不限流量,抗一般投诉,不抗版权投诉。 CPU很快,硬盘不错。 无大陆优化,但大陆连通性很不错,…...

H3C交换机的40G堆叠线 ,可以插在普通光口做堆叠吗?
环境: S6520X-24ST-SI交换机 H3C LSWM1QSTK2万兆40G堆叠线QSFP 问题描述: H3C交换机的40G堆叠线 ,可以插在普通光口做堆叠吗? 解答: 1.H3C交换机的40G堆叠线通常是用于连接堆叠模块或堆叠端口的。这些堆叠线通常使…...

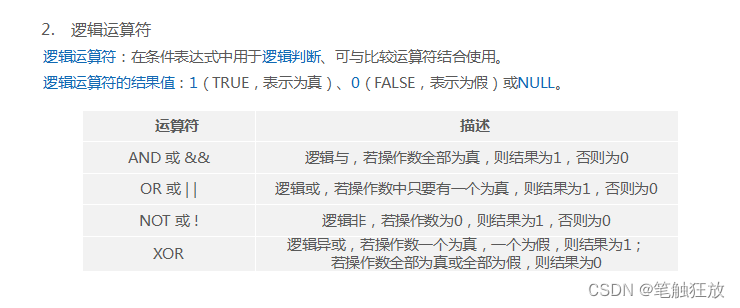
【Java 进阶篇】JavaScript三元运算符详解
JavaScript是一门广泛用于前端和后端开发的编程语言,具备强大的表达式和运算符。本篇博客将重点介绍JavaScript中的三元运算符,解释其语法、用法和示例。如果您是JavaScript初学者,或者希望更深入了解这门语言的运算符,那么这篇博…...
MySQL数据库技术笔记(4)
关系型数据库需要使用设计范式: 第一范式:遵从原子性,属性不可再分,数据库表的每一列都是不可分割的基本数据项,同一列中不能有多个值。 例如:需要创建一张地址表,存储地址信息。将地址信息划…...
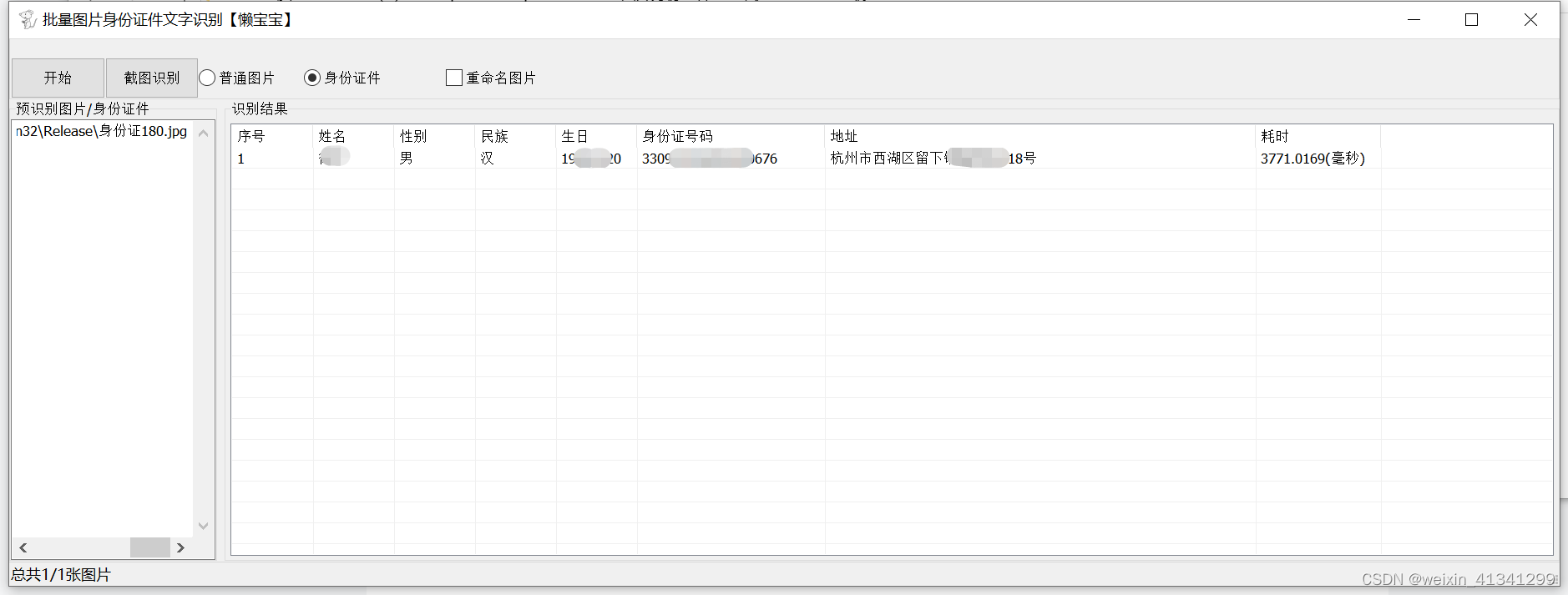
批量图片转文字识别OCR身份证件信息提取软件
现在的OCR软件很多,有在线的也有本地的,单识别文字功能还行,不过能批量识别的好像不多,网上搜了几个都不怎么好用。尤其是识别身份证件之类的软件,并且还能提取出识别到的信息,比如姓名 名族地址等等更少。…...
Mac/Wins Matlab如何查看APPs源码
查看Apps方法一样,点击HOME-preferences-MATLAB-Apps查看你的Apps安装路径。 你的Apps文件就安装在该目录下,直接进入这个目录就可以看到你自己写的APPs文件,...

Web应用-Thinkphp框架-开发指南
Thinkphp框架 二级导航分类,模板继承,内置标签Public 修改MVC模块化 ——访问机制传参加载模版模版引入 分离Runtime 缓存文件管理员添加数据验证及验证场景 控制器 validate 在sql执行(敏感操作)之前验证数据模板 分页数据表连接…...
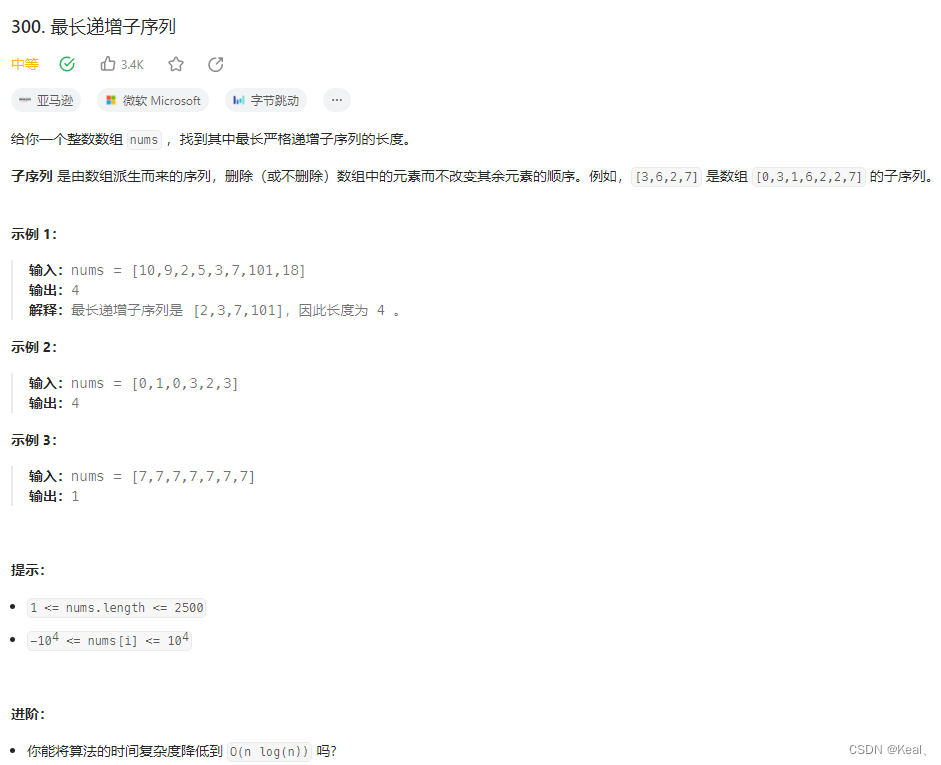
LeetCode【300】最长递增子序列
题目: 思路: 通常来说,子序列不要求连续,而子数组或子字符串必须连续;对于子序列问题,第一种动态规划方法是,定义 dp 数组,其中 dp[i] 表示以 i 结尾的子序列的性质。在处理好每个…...
JRebel在IDEA中实现热部署 (JRebel实用版)
JRebel简介: JRebel是与应用程序服务器集成的JVM Java代理,可使用现有的类加载器重新加载类。只有更改的类会重新编译并立即重新加载到正在运行的应用程序中,JRebel特别不依赖任何IDE或开发工具(除编译器外)。但是&…...

uniapp微信小程序之分包异步化之组件分包
一、组件分包异步化解决的问题 日渐增加的通用组件造成的主包空间不足; 提升小程序访问速度,降低白屏率; 二、开启组件分包异步化过程中遇到的问题 如何进行占位组件配置; 如何解决通过$refs访问异步组件报错; 如何判断所有异步组件都已加载完毕; 多分包组件之间互相调用…...
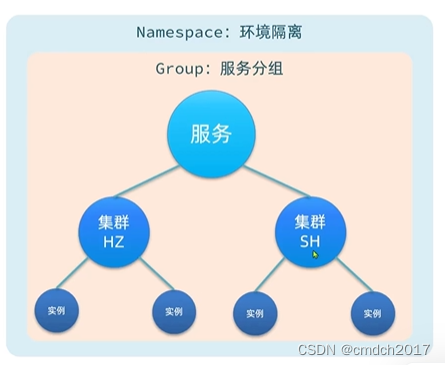
Nacos(替代Eureka)注册中心
Nacos初步学习 Nacos 是一个开源的服务注册和配置中心,它允许您注册、注销和发现服务实例,并提供了配置管理的功能。下面是Nacos的最基础用法: 1. 服务注册和发现: 首先,您需要将您的应用程序或服务注册到Nacos中。…...
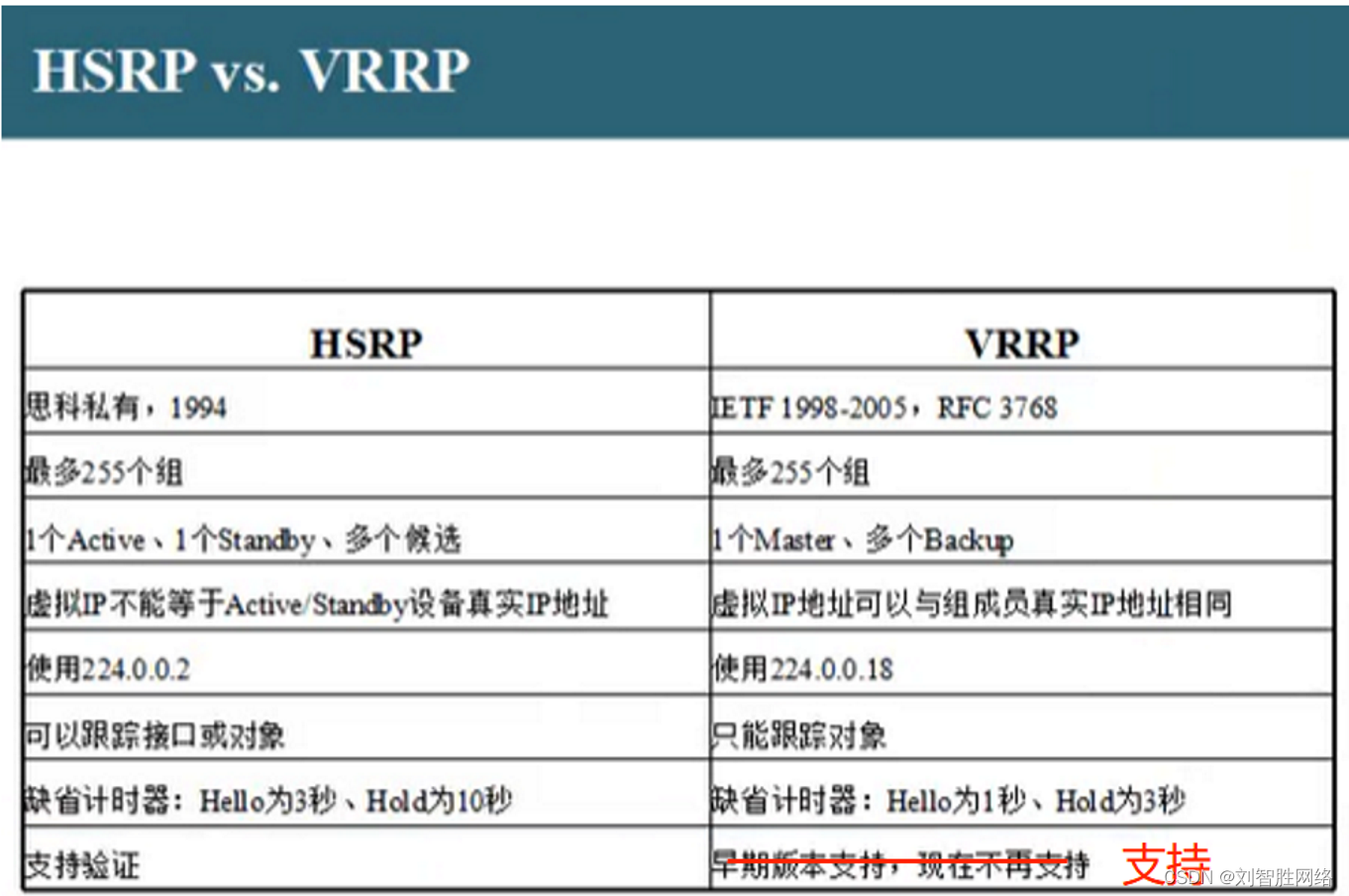
FHRP首跳冗余的解析
首跳冗余的解析 个人简介 HSRP hot standby router protocol 热备份路由协议 思科设备上 HSRP VRRP 华为设备上 VRRP HSRP v1 version 1 HSRP v2 version 2 虚拟一个HSRP虚拟IP地址 192.168.1.1 开启HSRP的抢占功能 通过其他参数 人为调整谁是主 谁是从 &a…...

垂直分表为什么能够加快查询效率?
前言 垂直分表是分库分表中分表操作上一个重要的实现方式,利用垂直分表可以提高数据的处理效率和查询速度,本节主要围绕 垂直分表为什么能够加快查询速度 展开说明,以mysql查询的底层流程为例。 垂直分表是将一张表按列分为多张表,…...

Linux网络基础知识全面总结
文章目录 linux网络基础知识1.1 IP地址和子网掩码1.2 网关和路由1.3 域名系统 (DNS)1.4 端口和协议 Linux网络配置2.1 ifconfig命令2.2 网络接口配置文件2.3 DHCP自动获取IP地址2.4 静态IP地址配置2.5 网络重启和应用配置3. 网络工具和命令3.1 ping命令3.2 traceroute和mtr命令…...

【arm实验2】按键中断事件控制实验
设置按键中断,按键1按下,LED亮,再次按下,灭 按键2按下,蜂鸣器叫,再次按下,停 按键3按下,风扇转,再次按下,停 主函数: linuxlinux:~/study/08-c$…...
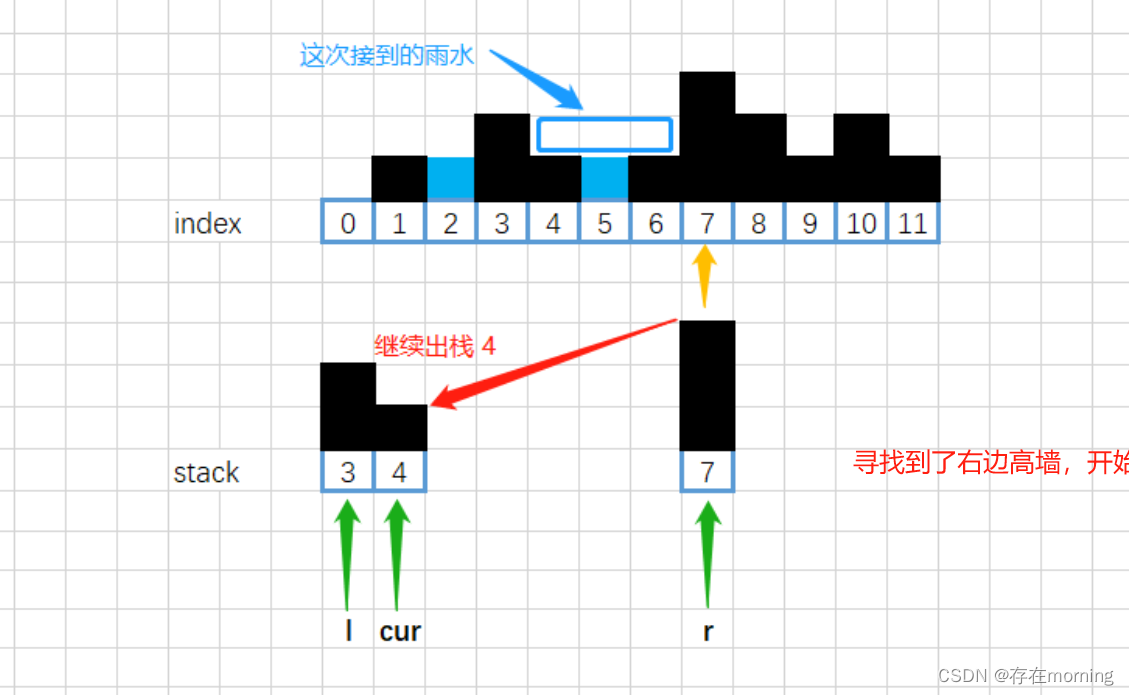
【数据结构-栈 二】【单调栈】每日温度、接雨水
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【单调栈的应用】,使用【栈】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&am…...

基于Keil a51汇编 —— 控制语句
ALIGN ALIGN expression ALIGN 语句将位置计数器设置为下一个地址模 2^表达式。 这可用于确保下一条语句在 2^n 边界上对齐。例如,对齐缓存行中的代码或数据。如有必要,汇编程序会创建一个间隙。间隔字节的内容因各个部分而异: 在data中未定…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
