数据结构与算法系列之插入排序

💗 💗 博客:小怡同学
💗 💗 个人简介:编程小萌新
💗 💗 如果博客对大家有用的话,请点赞关注再收藏 🌞
什么是插入排序
有一个已经有序的数据序列,要求在这个已经排好的数据序列中插入一个数,但要求插入后此数据序列仍然有序,这个时候就要用到一种新的排序方法–插入排序法
好比可以用打牌时对摸起的牌根据牌的点数来对其进行插入排列来描述。

实现思想
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与
array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移。 例如:
有一个有序区间,选其中一个数插入其中,这个数依次比较如果匹配失败则,换到下一个数比较。
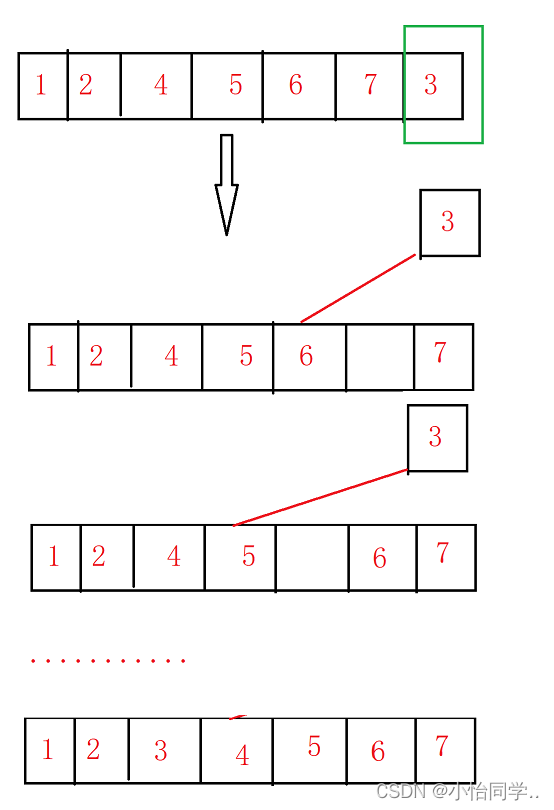
插入排序的时间复杂度
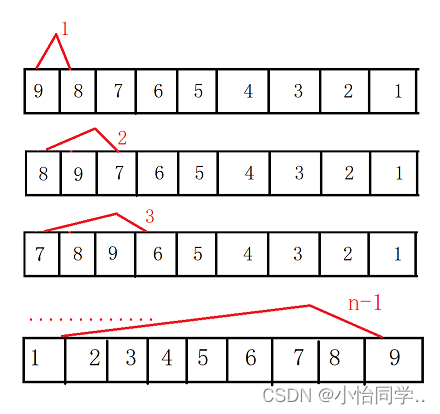
时间复杂度是O(n^2) 在最坏情况下逆序需要每个数轮流插入 根据等差数列 1+2+3+…+n-1
所以时间复杂度是O(n^2) 在最好情况下只需要轮一遍 所以时间复杂度为O(n^2)
插入排序的稳定性
稳定性意思是两个元素之间的相对位置没有改变 如 44 与 44 相等, 44在左 44在右,插入排序之后
44 仍在左 44 仍在右,这两个元素的相对位置没有改变。

代码实现
#include <stdio.h>
void InsertSort(int* arr, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = arr[end + 1];while (end >= 0){if (tmp <= arr[end]){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp;}}int main()
{int arr[] = { 1,2,4,5,6,7,8,9,3 };int n = (sizeof(arr) / sizeof(arr[0]));InsertSort(arr, n);for (int i = 0; i < n; i++){printf("%d ", arr[i]);}return 0;
}
插入排序的优化——希尔排序
什么是希尔排序
希尔排序又称缩小增量排序,它通过比较相距一定间隔的元素来进行,各趟比较所用的距离随着算法的进行而减小,直到只比较相邻元素的最后一趟排序为止。
通俗大意是:把原本一组的数组间断性分为几个数组,在对已经分完的数组进行插入排序。
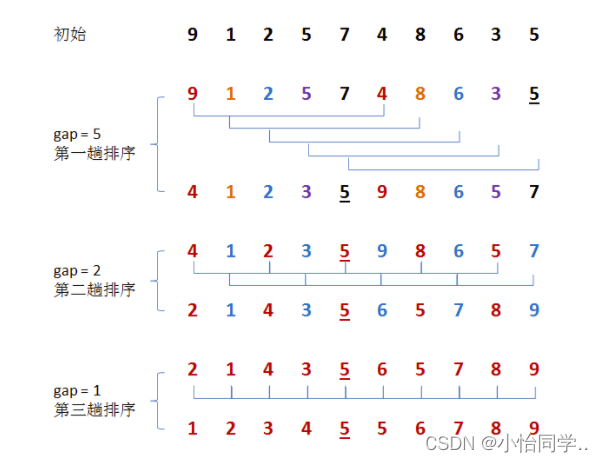
希尔排序的时间复杂度及稳定性
因为希尔排序的时间复杂度不好计算,因为gap的取值 方法很多,导致很难去计算。 时间复杂度;O(logNN)或者O(log3NN)
稳定性:不稳定
实现思想
先进行预排序,让数组接近有序,等到与排序之后 数组大多是有序的状态,大致上是有序数组,可进行插入排序。
void ShellSort(int* arr, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;//gap>1时是预排列 gap==1时相当有序排列for (int i = 0; i < n - gap; i += gap)//把间隔为gap的元素进行插入排序{int end = i;int tmp = arr[end + gap];while (end >= 0){if (tmp < arr[end]){arr[end + gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;}}
}int main()
{int arr[] = { 1,2,4,5,6,7,8,9,3 };int n = (sizeof(arr) / sizeof(arr[0]));InsertSort(arr, n);for (int i = 0; i < n; i++){printf("%d ", arr[i]);}return 0;
}

相关文章:

数据结构与算法系列之插入排序
💗 💗 博客:小怡同学 💗 💗 个人简介:编程小萌新 💗 💗 如果博客对大家有用的话,请点赞关注再收藏 🌞 什么是插入排序 有一个已经有序的数据序列,要求在这个已经排好的数…...

Text to image论文精读ALR-GAN:文本到图像合成的自适应布局优化
ALR-GAN是北京工业大学学者提出的一种自适应布局优化生成对抗网络,其可以在没有任何辅助信息的情况下自适应地优化合成图像的布局。 文章发表于2023年,IEEE Transactions on Multimedia(TMM)期刊(CCF B,JCR…...
windows版 redis在同一局域网下互联
项目场景: 同一局域网下各个主机互相连接同一个redis 问题描述 无法连接 原因分析: 没有放行对方的地址 解决方案: 修改配置文件 最重要的一步如下 然后把 redis.windows.conf的文件也照上面的修改一下保持一致 然后安装一下redis服务这…...

Near-Optimal Bayesian Online Assortment of Reusable Resources
摘要 受租赁服务在电子商务中的应用的激励,我们考虑为不同类型的到达消费者提供可重复使用资源的在线分类的收入最大化。我们针对贝叶斯环境中的最优在线策略设计了具有竞争力的在线算法,其中类型随时间独立于已知的异构分布绘制。在初始库存最小值cmin…...

数据库复习2
一. 简答题(共1题,100分) 1. (简答题) 存在数据库test,数据库中有如下表: 1.学生表 Student(Sno,Sname,Sage,Ssex) --Sno 学号,Sname 学生姓名,Sage 出生年月,Ssex 学生性别 主键Sno 2.教师表 Teacher(Tno,Tname) --T…...

公众号运营之竞品分析,教你拆解公众号
知己知彼,百战不殆,公众号运营亦是如此。 当运营者只关注自己账号的时候,很容易陷入某个误区中出不来。这个时候就要拓宽我们的视野,多去看看“外面的世界”,不要只局限于自己的一片小天地中。 看看同领域优秀公众号…...

python常见问题详解
Python python 没有多态,而是鸭子类型 多继承,没有接口,可通过语法糖实现接口的作用 lambda中只能有一句 "/"表示之前的参数是必须是位置参数,”**“表示是后面的必须是关键字参数 Python多进程 Python 多线程是伪多线…...
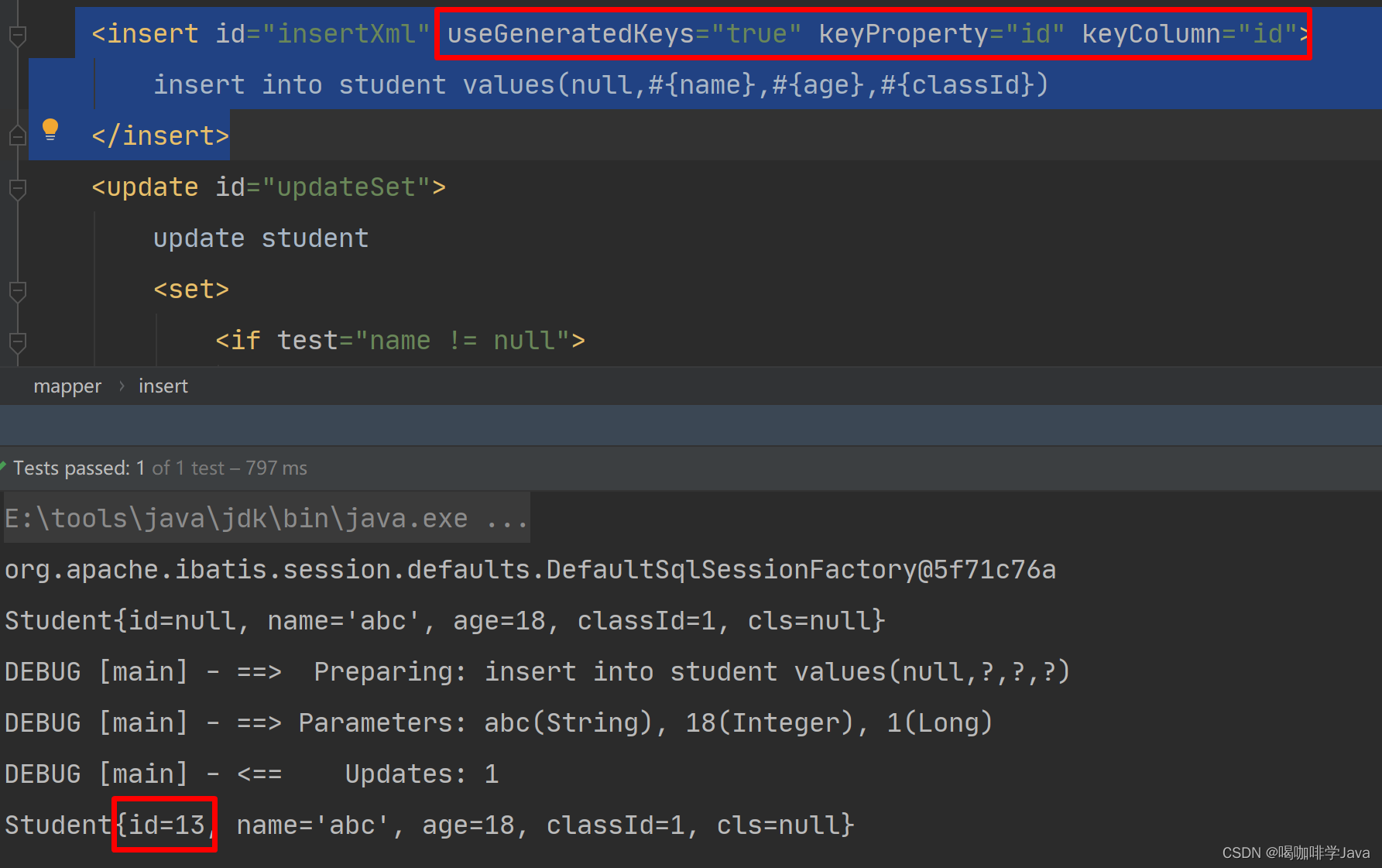
MyBatis-常用SQL操作
一、动态SQL 1.概述】 1.1动态SQL: 是 MyBatis 的强大特性之一,解决拼接动态SQL时候的难题,提高开发效 1.2分类: if choose(when,otherwise) trim(where,set) foreach 2.if 2.1 做 where 语句后面条件查询的,if 语句是可以…...
DSPE-PEG-TCO;磷脂-聚乙二醇-反式环辛烯科研用化学试剂简介
中文名称 磷脂-聚乙二醇-反式环辛烯 英文名称 DSPE-PEG-TCO 外观:粉末或半固体,取决于分子量。 溶剂:溶于大部分有机溶剂,如:DCM、DMF、DMSO、THF等等。在水中有很好的溶解性 稳定性:冷藏保存ÿ…...
)
华为OD机试真题Java实现【最小施肥机能效】真题+解题思路+代码(20222023)
最小施肥机能效 某农场主管理了一大片果园,fields[i]表示不同果林的面积,单位:( m 2 m^2 m2),现在要为所有的果林施肥且必须在 n 天之内完成,否则影响收成。 小布是果林的工作人员,他每次选择一片果林进行施肥,且一片果林施肥完后当天不再进行施肥作业。 假设施肥机的…...

【问题记录】【排查问题的方法总结】vue3中数据失去响应式?为什么数据变了,视图只更新了一次就不再更新了?
一、问题概述: 持续请求的数据变动之后,控制台输出绑定的响应式变量 mapObj 的确变了,但是视图上只更新了一次,后续就不再更新了。 二、排查过程: PC上用定时器setInterval模拟数据(全是小于0的数据)更新࿰…...

基于遗传算法的柔性生产调度研究(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

Heroku的12条准则
I. Codebase One codebase tracked in revision control, many deploys 要有代码仓库,多版本控制,如使用git来管理代码仓库。 II. Dependencies Explicitly declare and isolate dependencies 明确声明依赖,隔离依赖。强依赖往往会导致连…...
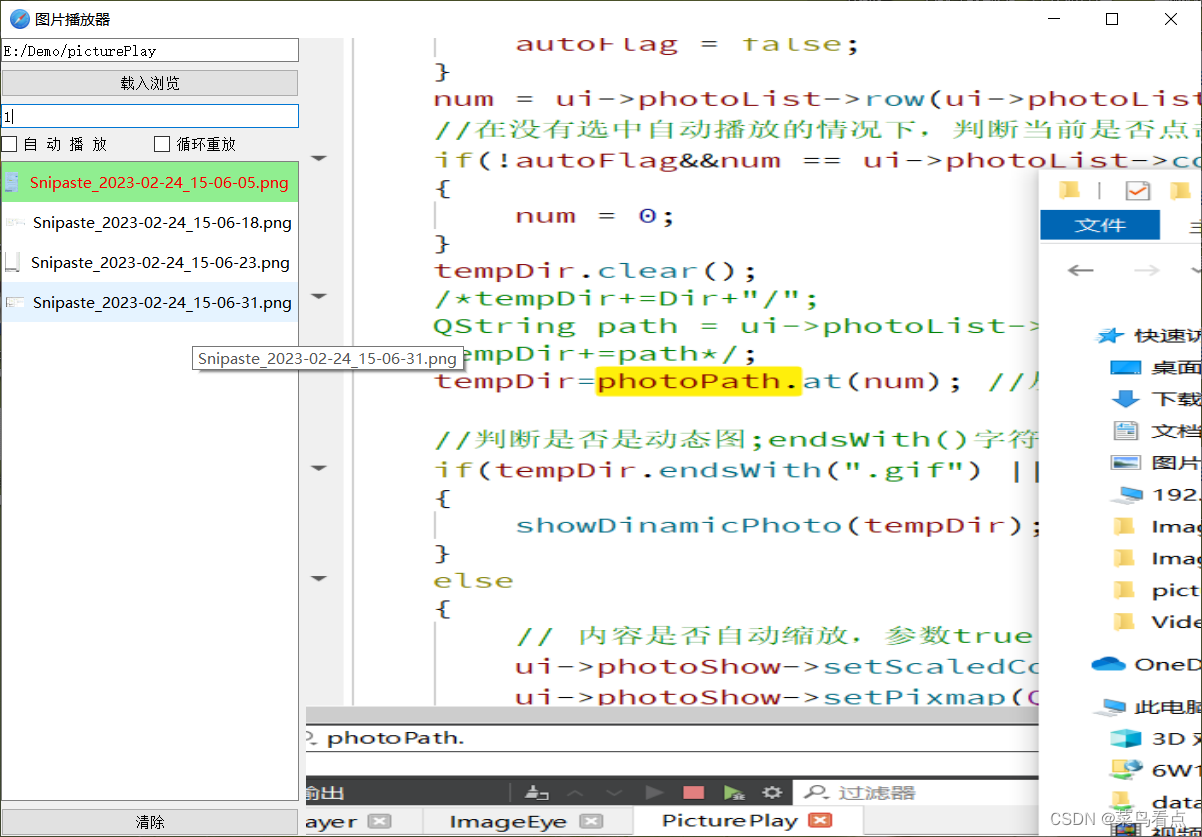
Qt图片定时滚动
目录参考结构PicturePlay.promain.cpppictureplay.hpictureplay.cpppictureplay.ui效果参考 Qt图片浏览器 QT制作一个图片播放器 Qt中自适应的labelpixmap充满窗口后,无法缩小只能放大 可以显示jpg、jpeg、png、bmp。可以从电脑上拖动图到窗口并显示出来或者打开文件…...
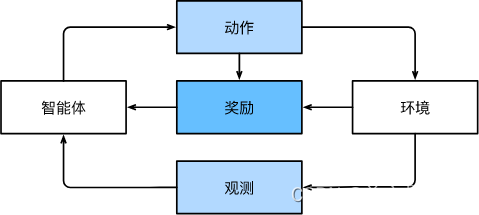
深度学习引言
动手学深度学习pytorch版-笔记原文链接日常生活中的机器学习机器学习中的关键组件数据模型目标函数优化算法各种机器学习问题监督学习回归分类标记问题搜索推荐系统序列学习无监督学习与环境互动强化学习特点小结原文链接 动手学深度学习pytorch中文版 日常生活中的机器学习 …...

ESP32 WIFI使用介绍
ESP32 WIFI 概述 WIFI 库支持配置及监控 ESP32 WIFI 连网功能。支持配置 station 模式(即 STA 模式或 WIFI 客户端模式),此时 ESP32 连接到接入点(AP)。AP 模式(即 soft-AP 模式或接入点模式)&…...

JavaEE简单实例——MyBatis的一对一映射的嵌套查询的简单介绍和基础配置
简单介绍: 在前一章我们介绍了关于MyBatis的多表查询的时候的对应关系,其中有三种对应关系,分别是一对一,一对多,多对多的关系。如果忘记了这三种方式的对应形式可以去前面看看,一定要记住这三种映射关系的…...
(1))
详解指针(进阶版)(1)
前言:总篇章分为(1)和(2),本篇内容包括:指针数组,数组指针,&数组名与数组名的区分 数组传参 ,函数指针,函数指针数组 part 1:指…...

【OJ】盐荒子孙
📚Description: 盐体图 盐是对人类生存具有重要意义的物质之一。当中国古人从肉食为主转向谷食为主的时候,吃盐的需求就发生了,因为动物血肉里面包含有足够人体所需的盐分,而谷 物本身不包含盐分。在长达几十万年的旧石器时代&…...

Java数据结构 —— 手写线性结构(稀疏数组、栈、队列、链表)
目录 稀疏数组 顺序表 链表 单向顺序链表 双向链表 双向循环链表求解约瑟夫环(Joseph) 栈 顺序栈 队列 顺序队列 顺序循环队列 稀疏数组 当一个数组中大部分值为0,或者相同时,可以采用稀疏数组的方式来保存,从而节约存储…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
