1 随机事件与概率
首先声明【这个括号内的都是批注】
文章目录
- 1 古典概型求概率
- 1.1 随机分配问题【放球】
- 例子
- 1.2 简单随机抽样问题【取球】
- 例子
- 2 几何概型求概率
- 例子
- 3 重要公式求概率
- 3.1 对立
- 3.2 互斥
- 3.3 独立
- 3.4 条件(要做分母的必须大于0)
- 例子
- 3.5 不等式或包含
- 例子
- 3.6 最值【被包含的往往更小,即交集往往被并集包含】
- 例子
- 4 事件独立性的判定
- 4.1 定义
- 4.2 判定【只要独立,咋都独立】
- 例子
1 古典概型求概率
1.1 随机分配问题【放球】
将n个球随机放到N个盒子中
| 放的方式 | 放的总数 |
|---|---|
| 每个盒子可以放多个球 | N n N^n Nn |
| 每个盒子只能放一个球 | P N n P_N^n PNn |
例子
1. 将n个球随机放入 N ( n ≤ N ) N(n≤N) N(n≤N)个盒子中,每个盒子可以放任意多个球,球下列事件的概率:
A={某指定n个盒子各有一球},B={恰有n个盒子各有一球},C={指定k(k≤n)个盒子各有一球}
【分析:题给每个盒子可以放任意多个球,所以基本事件总数为 N n N^n Nn,置于分母 。分子上是给定条件下的总数:对于A和C,指定代表仅一种情况;对于B,恰有n个代表 C N n C_N^n CNn】
n个盒子各有1球有 n ! n! n!种放法: p ( A ) = 1 × n ! N n , p ( B ) = [ C N n × n ! ] / N n p(A)=\frac {1×n!} {N^n},p(B)=[C_N^n×n!]/N^n p(A)=Nn1×n!,p(B)=[CNn×n!]/Nn
先从n个球中选k个球有 C N n C^n_N CNn种选法,k个盒子各有1球有 k ! k! k!种放法,还剩下 ( n − k ) (n-k) (n−k)个球要放在 ( N − k ) (N-k) (N−k)个盒子里有 ( N − k ) ( n − k ) (N-k)^{(n-k)} (N−k)(n−k)种放法: p ( C ) = [ C N n × k ! × ( N − k ) ( n − k ) ] / N n p(C)=[C^n_N×k!×(N-k)^{(n-k)}]/N^n p(C)=[CNn×k!×(N−k)(n−k)]/Nn
2. 有12个人回母校参加校庆,每个人在365天哪一天出生等可能,则
A 1 = { 生日分别为每个月的第一天 } A_1=\{生日分别为每个月的第一天\} A1={生日分别为每个月的第一天};
B 1 = { 生日全不相同 } B_1=\{生日全不相同\} B1={生日全不相同}; B 1 ‾ = { 至少有 2 人生日相同 } \overline{B_1}=\{至少有2人生日相同\} B1={至少有2人生日相同};
C 1 = { 有且仅有三个人的生日分别在劳动节、儿童节、中秋节 } C_1=\{有且仅有三个人的生日分别在劳动节、儿童节、中秋节\} C1={有且仅有三个人的生日分别在劳动节、儿童节、中秋节}。
【分析:12个球放入365个盒子中,每个盒子可以放任意多个球。 A 1 A_1 A1与 C 1 C_1 C1对应1.1中的A和C,都是指定; B 1 B_1 B1对应1.1中的B】
p ( A ) = [ 1 × 12 ! ] / 36 5 12 , p ( B 1 ) = [ C 365 12 × 12 ! ] / 36 5 12 , p ( B 1 ‾ ) = 1 − p ( B 1 ) p(A)=[1×12!]/365^{12},p(B_1)=[C_{365}^{12}×12!]/365^{12},p(\overline{B_1})=1-p(B_1) p(A)=[1×12!]/36512,p(B1)=[C36512×12!]/36512,p(B1)=1−p(B1)
p ( C 1 ) = [ C 12 3 × 3 ! × ( 365 − 3 ) ( 12 − 3 ) ] / 36 5 12 p(C_1)=[C_{12}^{3}×3!×(365-3)^{(12-3)}]/365^{12} p(C1)=[C123×3!×(365−3)(12−3)]/36512
1.2 简单随机抽样问题【取球】
在含 N N N个球的盒子中进行n次简单随机抽样
| 取的方式 | 取的总数 |
|---|---|
| 【拿了还在】先后有放回取 n n n次 | N n N^n Nn |
| 【拿了就没了】先后无放回取 n n n次 | P N n P_N^n PNn |
| 【拿了就没了】任取 n n n个 | C N n C_N^n CNn |
可以发现,无放回和任取,其实是一个意思的不同表达,只不过任取是没按照顺序随便取的,而无放回是按顺序一个一个取的。但是,无放回取n个和任取n个,都是从总数中拿走了n个,因此在计算的时候可以将无放回按照任取来算,因为在计算过程中,无放回的顺序是会被抵消的。
即:“先后无放回取n个球”与“任取n个球”的概率相同
例子



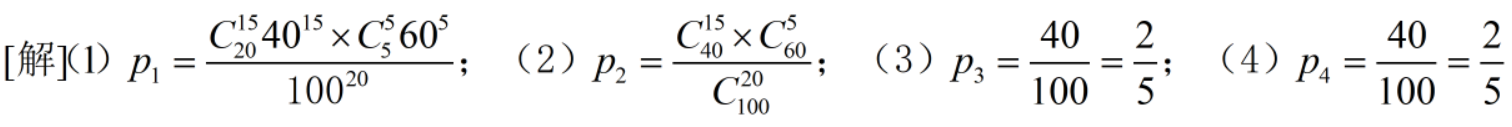
抓阄模型即盲盒抽签。(3)(4)就是:不管你是否有放回,我闭着眼睛取,就是不看取到的是什么球,但从100个球里面取到白球的概率都是等可能的2/5,所以不管取几次,取到白球的概率都是不变的。
比如有100个人买彩票,其中有一张彩票是有奖的,那么获奖的总概率是1/100,我是第51个买到彩票的,但我获奖的概率依然是1/100,因为我不知道前面买了彩票的人是否中奖了。
但如果是100张刮刮奖,由一张刮刮奖是有奖的,还没刮之前,每张获奖概率是1/100。前面50个人买了,且现场刮开了,发现都没有奖,那么有奖的在还剩下的5张刮刮奖里面,此时我再去买,获奖概率就变成了50/100=1/2。这就不是抓阄模型了,抓阄模型是事先都不知道对方有没有中奖,而这是已知有多少人没中奖的情况下,我能中奖的概率,为条件概率模型。
2 几何概型求概率
若全集是一个几何区域,样本点落入某一子区域的概率是:子区域的面积与总区域面积之比。
例子


3 重要公式求概率
3.1 对立
①德·摩根定律【长杠变短杠,开口换方向】:
A ∪ B ‾ = A ‾ ∩ B ‾ , A B ‾ = A ‾ ∪ B ‾ \overline{A∪B}=\overline{A}∩\overline{B},\overline{AB}=\overline{A}∪\overline{B} A∪B=A∩B,AB=A∪B
② P ( A ) = 1 − P ( A ‾ ) P(A)=1-P(\overline{A}) P(A)=1−P(A)
3.2 互斥
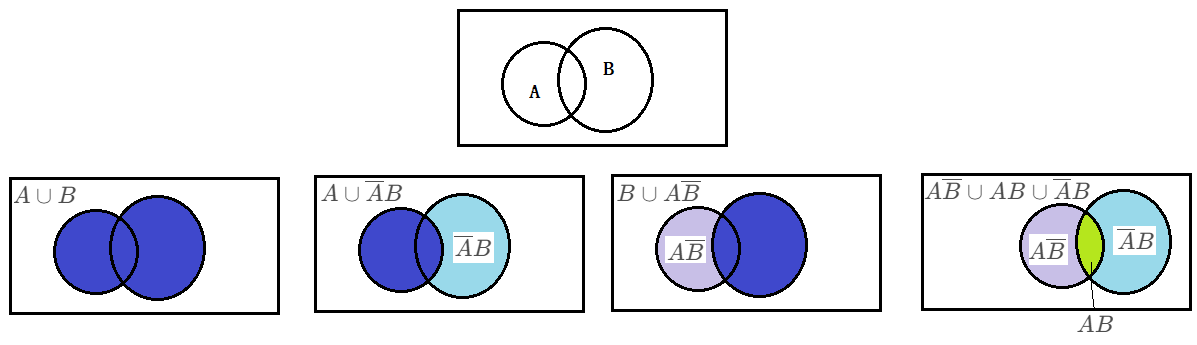
① A ∪ B = A ∪ A ‾ B = B ∪ A B ‾ = A B ‾ ∪ A B ∪ A ‾ B A∪B=A∪\overline{A}B=B∪A\overline{B}=A\overline{B}∪AB∪\overline{A}B A∪B=A∪AB=B∪AB=AB∪AB∪AB.
②若 B 1 , B 2 , B 3 B_1,B_2,B_3 B1,B2,B3为完备事件组,即 Ω = B 1 ∪ B 2 ∪ B 3 Ω=B_1∪B_2∪B_3 Ω=B1∪B2∪B3,
则 A = A Ω = A ( B 1 ∪ B 2 ∪ B 3 ) = A B 1 ∪ A B 2 ∪ A B 3 A=AΩ=A(B_1∪B_2∪B_3)=AB_1∪AB_2∪AB_3 A=AΩ=A(B1∪B2∪B3)=AB1∪AB2∪AB3
③ P ( A − B ) = P ( A B ‾ ) = P ( A ) − P ( A B ) P(A-B)=P(A\overline{B})=P(A)-P(AB) P(A−B)=P(AB)=P(A)−P(AB)
容易得到:若 P ( A B ‾ ) = P ( A ‾ B ) P(A\overline{B})=P(\overline{A}B) P(AB)=P(AB),则 P ( A ) = P ( B ) P(A)=P(B) P(A)=P(B)
④
a. P ( A + B ) = P ( A ) + P ( B ) − P ( A B ) P(A+B)=P(A)+P(B)-P(AB) P(A+B)=P(A)+P(B)−P(AB)
b. P ( A + B + C ) = P ( A ) + P ( B ) + P ( C ) − P ( A B ) − P ( A C ) − P ( B C ) + P ( A B C ) P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC) P(A+B+C)=P(A)+P(B)+P(C)−P(AB)−P(AC)−P(BC)+P(ABC)
c.若 A , B , C A,B,C A,B,C两两互斥,则 P ( A ∪ B ∪ C ) = P ( A ) + P ( B ) + P ( C ) P(A∪B∪C)=P(A)+P(B)+P(C) P(A∪B∪C)=P(A)+P(B)+P(C)
3.3 独立
①若 A , B , C A,B,C A,B,C相互独立,则 P ( A B C ) = P ( A ) P ( B ) P ( C ) P(ABC)=P(A)P(B)P(C) P(ABC)=P(A)P(B)P(C)
①若 A , B , C A,B,C A,B,C相互独立,则
P ( A ∪ B ∪ C ) = 1 − P ( A ∪ B ∪ C ‾ ) = 1 − P ( A ‾ B ‾ C ‾ ) = 1 − P ( A ‾ ) P ( B ‾ ) P ( C ‾ ) P(A∪B∪C)=1-P(\overline{A∪B∪C})=1-P(\overline{A}\overline{B}\overline{C})=1-P(\overline{A})P(\overline{B})P(\overline{C}) P(A∪B∪C)=1−P(A∪B∪C)=1−P(ABC)=1−P(A)P(B)P(C)
3.4 条件(要做分母的必须大于0)
① P ( A ∣ B ) = P ( A B ) P ( B ) ( P ( B ) > 0 ) P(A|B)=\frac{P(AB)}{P(B)}(P(B)>0) P(A∣B)=P(B)P(AB)(P(B)>0)
② P ( A B ) = P ( B ) P ( A ∣ B ) = P ( A ) P ( B ∣ A ) = P ( A ) + P ( B ) − P ( A + B ) = P ( A ) − P ( A B ‾ ) P(AB)=P(B)P(A|B)=P(A)P(B|A)=P(A)+P(B)-P(A+B)=P(A)-P(A\overline{B}) P(AB)=P(B)P(A∣B)=P(A)P(B∣A)=P(A)+P(B)−P(A+B)=P(A)−P(AB)
③【全概率公式(知因求果):已知在各个因素下B会发生的概率,去求B发生的概率】
若 A 1 , A 2 , A 3 A_1,A_2,A_3 A1,A2,A3为完备事件组, P ( A i ) > 0 ( i = 1 , 2 , 3 ) P(A_i)>0(i=1,2,3) P(Ai)>0(i=1,2,3),则
P ( B ) = P ( A 1 ) P ( B ∣ A 1 ) + P ( A 2 ) P ( B ∣ A 2 ) + P ( A 3 ) P ( B ∣ A 3 ) P(B)=P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+P(A_3)P(B|A_3) P(B)=P(A1)P(B∣A1)+P(A2)P(B∣A2)+P(A3)P(B∣A3)
④【贝叶斯公式(执果索因):已知B已经发生了,那么是哪个因素导致的?】
若 A 1 , A 2 , A 3 A_1,A_2,A_3 A1,A2,A3为完备事件组, P ( A i ) > 0 ( i = 1 , 2 , 3 ) P(A_i)>0(i=1,2,3) P(Ai)>0(i=1,2,3),则
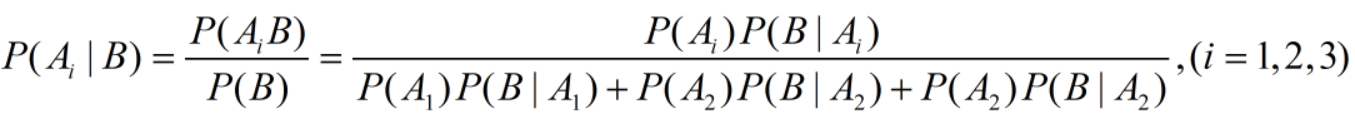
例子
- 设有甲、乙两名射击运动员,甲命中目标的概率是0.6,乙命中目标的概率是0.5,求下列事件的概率。
(1)从甲、乙中任选一人去射击,若命中,则是甲命中的概率;【事件来自不同阶段→贝叶斯公式】
(2)甲、乙两人各自独立射击,若目标命中,则是甲命中的概率.【事件来自相同阶段→条件概率】

3.5 不等式或包含
① 0 ≤ P ( A ) ≤ 1 0≤P(A)≤1 0≤P(A)≤1.
② 若 A ⊆ B ,则 P ( A ) ≤ P ( B ) 若A⊆B,则P(A)≤P(B) 若A⊆B,则P(A)≤P(B).
③ 由于 A B ⊆ A ⊆ A + B ,故 P ( A B ) ≤ P ( A ) ≤ P ( A + B ) 由于AB⊆A⊆A+B,故P(AB)≤P(A)≤P(A+B) 由于AB⊆A⊆A+B,故P(AB)≤P(A)≤P(A+B).
若当事件 A , B 同时发生时,事件 C 必然发生,则 A B ⊆ C 若当事件A,B同时发生时,事件C必然发生,则AB⊆C 若当事件A,B同时发生时,事件C必然发生,则AB⊆C
P ( A B ) = P ( A ) + P ( B ) − P ( A ∪ B ) = P ( A ) + P ( B ) − 1 ≤ P ( C ) P(AB)=P(A)+P(B)-P(A∪B)=P(A)+P(B)-1≤P(C) P(AB)=P(A)+P(B)−P(A∪B)=P(A)+P(B)−1≤P(C)
例子
1. 事件 A 与 B 相互独立, 1.事件A与B相互独立, 1.事件A与B相互独立, P ( A ) = a P(A)= a P(A)=a , P ( B ) = b ,P(B)=b ,P(B)=b, 若事件 C 发生必然导致 A 与 B 同时发生 , 那么 A , B , C 都不发生的概率为? 若事件C发生必然导致A与B同时发生,那么A,B,C都不发生的概率为? 若事件C发生必然导致A与B同时发生,那么A,B,C都不发生的概率为?
【分析:C发生会导致A,B同时发生,说明C在AB内,只有A和B同时发生C才会发生,单独发生的话C是不一定会发生的。而C若是不发生,那么可以推出要么是A不发生,要么是B不发生。题目所求的是A,B,C都不发生的概率,既然C不发生的话要么就是A不发生要么就是B不发生,那么A,B,C都不发生的概率不就是A,B都不发生的概率了。】
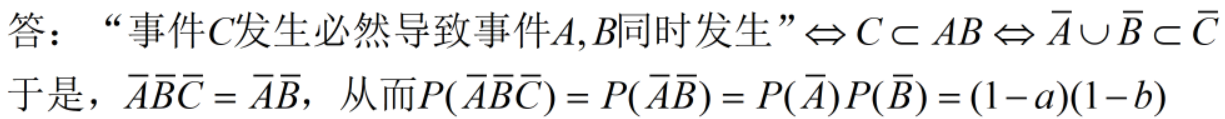
3.6 最值【被包含的往往更小,即交集往往被并集包含】
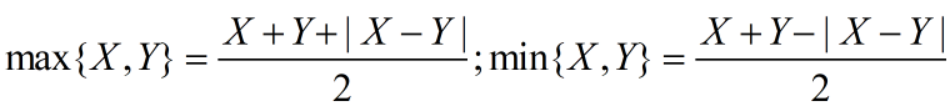
① { m a x { X , Y } ≤ a } = { X ≤ a } ∩ { Y ≤ a } \{max\{X,Y\}≤a\}=\{X≤a\}∩\{Y≤a\} {max{X,Y}≤a}={X≤a}∩{Y≤a}【最大的都比a小,那都比a小】【且】
② { m a x { X , Y } > a } = { X > a } ∪ { Y > a } \{max\{X,Y\}>a\}=\{X>a\}∪\{Y>a\} {max{X,Y}>a}={X>a}∪{Y>a}【求最大要的比a大,那要么X大于a,要么Y大于a】【或】
③ { m i n { X , Y } ≤ a } = { X ≤ a } ∪ { Y ≤ a } \{min\{X,Y\}≤a\}=\{X≤a\}∪\{Y≤a\} {min{X,Y}≤a}={X≤a}∪{Y≤a}【求最小的要比a小,那要么X小于等于a,要么Y小于等于a】【或】
④ { m i n { X , Y } > a } = { X > a } ∩ { Y > a } \{min\{X,Y\}>a\}=\{X>a\}∩\{Y>a\} {min{X,Y}>a}={X>a}∩{Y>a}【最小的都比a大,那都比a大】【且】
⑤ { m a x { X , Y } ≤ a } ⊆ { m i n { X , Y } ≤ a } \{max\{X,Y\}≤a\}⊆\{min\{X,Y\}≤a\} {max{X,Y}≤a}⊆{min{X,Y}≤a}【且⊆或】
⑥ { m i n { X , Y } > a } ⊆ { m a x { X , Y } > a } \{min\{X,Y\}>a\}⊆\{max\{X,Y\}>a\} {min{X,Y}>a}⊆{max{X,Y}>a}【且⊆或】
【补充:同号考交集,不同号考全概率公式】
例子
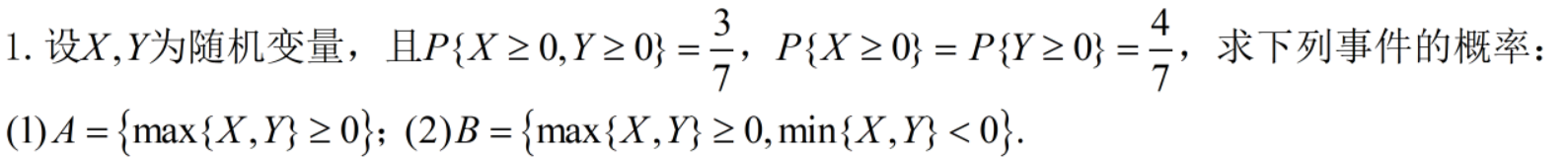
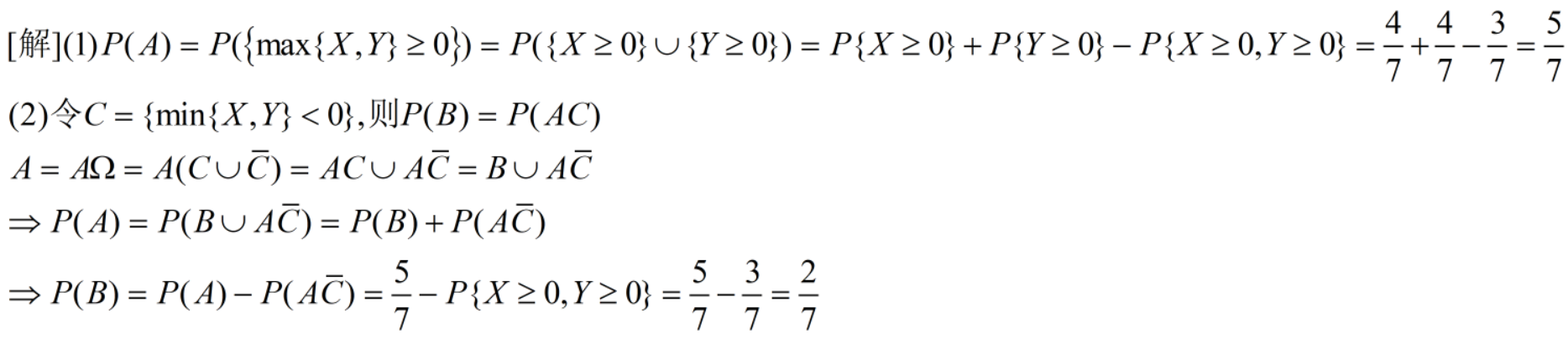
4 事件独立性的判定
4.1 定义
设 A , B 为两个事件,若 P ( A B ) = P ( A ) P ( B ) ,则称事件 A 与 B 相互独立 . 设A,B为两个事件,若P(AB)=P(A)P(B),则称事件A与B相互独立. 设A,B为两个事件,若P(AB)=P(A)P(B),则称事件A与B相互独立.
若对于 A , B , C 三个事件: 若对于A,B,C三个事件: 若对于A,B,C三个事件:
① P ( A B ) = P ( A ) P ( B ) ①P(AB)=P(A)P(B) ①P(AB)=P(A)P(B)
② P ( A C ) = P ( A ) P ( C ) ②P(AC)=P(A)P(C) ②P(AC)=P(A)P(C)
③ P ( B C ) = P ( B ) P ( C ) ③P(BC)=P(B)P(C) ③P(BC)=P(B)P(C)
④ P ( A B C ) = P ( A ) P ( B ) P ( C ) ④P(ABC)=P(A)P(B)P(C) ④P(ABC)=P(A)P(B)P(C)
若①②③④同时满足,则称事件 A , B , C 相互独立 若①②③④同时满足,则称事件A,B,C相互独立 若①②③④同时满足,则称事件A,B,C相互独立
若仅④不满足,则称事件 A , B , C 两两独立 若仅④不满足,则称事件A,B,C两两独立 若仅④不满足,则称事件A,B,C两两独立
4.2 判定【只要独立,咋都独立】

例子
设随机事件A与B相互独立, 0 < P ( A ) < 1 , P ( C ) = 1 0<P(A)<1,P(C)=1 0<P(A)<1,P(C)=1,则下列事件中不相互独立的是(C)
( A ) A , B , A ∪ C (A)A,B,A∪C (A)A,B,A∪C
( B ) A , B , A − C (B)A,B,A-C (B)A,B,A−C
( C ) A , B , A C (C)A,B,AC (C)A,B,AC
( D ) A , B , A ‾ ∩ C ‾ (D)A,B,\overline{A}∩\overline{C} (D)A,B,A∩C
【分析】 A ‾ ∩ C ‾ = A ∪ C ‾ = 1 − A ∪ C \overline{A}∩\overline{C}=\overline{A∪C}=1-A∪C A∩C=A∪C=1−A∪C,若选A则D也必须选,所以同时排除A和D
由 P ( C ) = 1 得 P ( C ‾ ) = 0 , 所以 P ( A − C ) = P ( A C ‾ ) = P ( A ) P ( C ‾ ) = 0 ,排除 B 由P(C)=1得P(\overline{C})=0,所以P(A-C)=P(A\overline{C})=P(A)P(\overline{C})=0,排除B 由P(C)=1得P(C)=0,所以P(A−C)=P(AC)=P(A)P(C)=0,排除B
对于选项C, P ( A C ) = P ( A ) P ( C ) = P ( A ) ≠ 0 P(AC)=P(A)P(C)=P(A)≠0 P(AC)=P(A)P(C)=P(A)=0,所以选C
相关文章:

1 随机事件与概率
首先声明【这个括号内的都是批注】 文章目录 1 古典概型求概率1.1 随机分配问题【放球】例子 1.2 简单随机抽样问题【取球】例子 2 几何概型求概率例子 3 重要公式求概率3.1 对立3.2 互斥3.3 独立3.4 条件(要做分母的必须大于0)例子 3.5 不等式或包含例…...

计算机视觉--通过HSV和YIQ颜色空间处理图像噪声
计算机视觉 文章目录 计算机视觉前言一、实现步骤二、实现总结 前言 利用HSV和YIQ颜色空间处理图像噪声。在本次实验中,我们使用任意一张图片,通过RGB转HSV和YIQ的操作,加入了椒盐噪声并将其转换回RGB格式,最终实现对图像的噪声处…...
WPF中prism模块化
1、参照(wpf中prism框架切换页面-CSDN博客)文中配置MainView和MainViewModel 2、模块其实就是引用类库,新建两个类库ModuleA ModuleB,修改输出类型为类库,并配置以下文件: ModuleA ModuleAProfile ModuleB Module…...

MyBatis基础之注解与SQL 语句构建器
文章目录 注解实现简单增删改查SQL 语句构建器SelectProvider举例 注解实现简单增删改查 在 MyBatis 的核心配置文件中,你需要配置的不是 mapper 映射文件,而是 Mapper 接口所在的包路径。 <!-- 在配置文件中 关联包下的 接口类--> <mappers&…...

Spring Boot项目搭建流程
Spring Boot是一款基于Spring Framework的开源框架,用于快速构建独立的、可运行的、生产级的Spring应用程序。它通过自动化配置、减少样板代码和默认的项目结构,极大地简化了Spring应用程序的开发过程。本文将详细介绍Spring Boot项目搭建的流程。 一、…...

VSCode插件开发之contributes和命令
VSCode插件开发 package.jsoncontributesconfigurationconfigurationDefaultscommandsmenuskeybindingsviewsviewsContainerscustomEditors 命令回调参数函数编辑器命令执行命令获取所有命令复杂命令 package.json contributes 之前说到 package.json 是 vscode 扩展的清单文…...

适用于Windows的远程传输大文件软件!
AnyViewer可在设备之间快速的远程传输文件,并支持远程传输大文件,传输速度可达10MB/S,同时,还可以传输单个文件不超过1TB的文件,并它基于椭圆曲线加密(ECC)加密,可保护您的文件不被…...
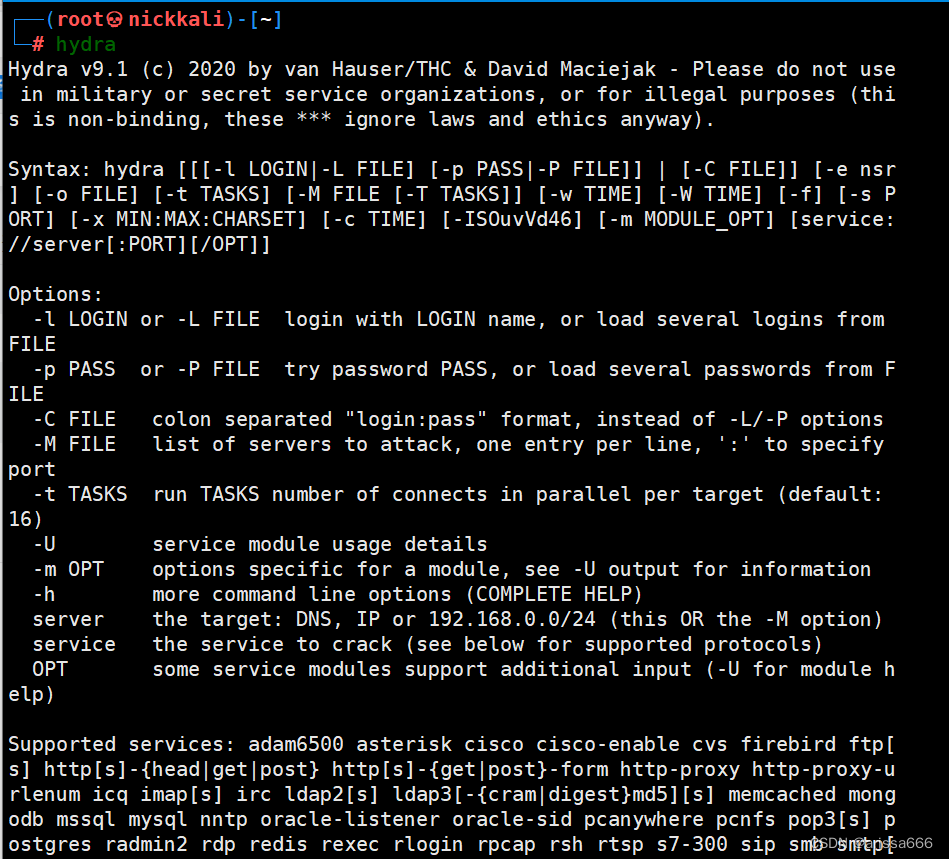
Hydra参数
kali的hyda参数 参数: hydra [[[-l LOGIN|-L FILE] [-p PASS|-P FILE]] | [-C FILE]] [-e ns][-o FILE] [-t TASKS] [-M FILE [-T TASKS]] [-w TIME] [-f] [-s PORT] [-S] [-vV] server service [OPT] -R 继续从上一次进度接着破解。 -S 采用SSL链接。 -s PORT 可通…...
R语言的计量经济学实践技术应用
计量经济学通常使用较小样本,但这种区别日渐模糊,机器学习在经济学领域、特别是经济学与其它学科的交叉领域表现日益突出,R语言是用于统计建模的主流计算机语言,在本次培训中,我们将从实际应用出发,重点从数…...
基于Springboot实现体质测试数据分析平台管理系统项目【项目源码+论文说明】
基于Springboot实现体质测试数据分析平台系统演示 摘要 随着科学技术的飞速发展,社会的方方面面、各行各业都在努力与现代的先进技术接轨,通过科技手段来提高自身的优势,体质测试数据分析及可视化设计当然也不能排除在外。体质测试数据分析及…...

JavaScript 严格模式
JavaScript 严格模式是一种在 JavaScript 编程中使用的特殊模式。它提供了一种更严格的语法和错误检查,以帮助开发者编写更可靠、更安全的代码。 使用严格模式的方法是在代码文件或函数的顶部添加如下语句: "use strict"; 作用:…...

安全与隐私:直播购物App开发中的重要考虑因素
随着直播购物App的崭露头角,开发者需要特别关注安全性和隐私问题。本文将介绍在直播购物App开发中的一些重要安全和隐私考虑因素,并提供相关的代码示例。 1. 数据加密 在直播购物App中,用户的个人信息和支付信息是极为敏感的数据。为了保护…...

Redis cluster 集群
redis集群redis集群是一个提供在多个redis节点间共享数据的程序集,redis集群可以支持多个master Redis集群支持多个master,每个master又可以挂载多个slave 读写分离、支持数据的高可用、支持海量数据的读写存储操作由于Cluster自动Sentinel的故障转移机制ÿ…...

服务器与网站部署知识体系目录
1.网站部署必备知识与实践操作 服务器全套基础知识:包含基本概念,作用,服务器选择,服务器管理等域名相关基础知识普及域名备案流程(个人备案,腾讯云 / 阿里云)将网站域名访问从http升级到https…...
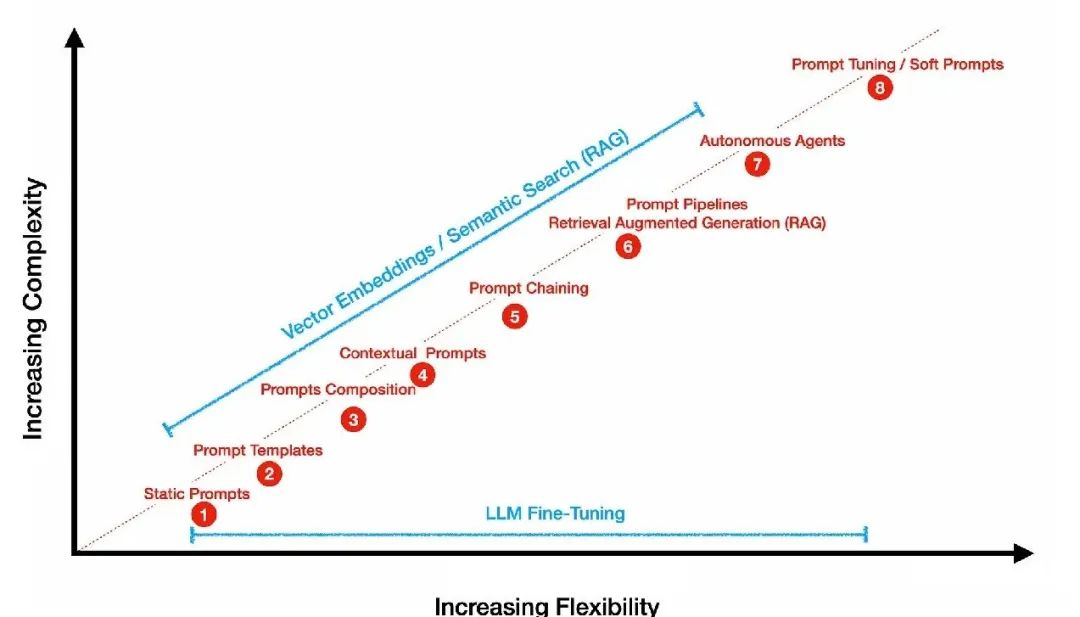
解读提示工程(Prompt Engineering)
提示工程(Prompt Engineering),也称为上下文提示,是一种通过不更新模型的权重/参数来引导LLM行为朝着特定结果的方法。这是与AI有效交流所需结果的过程。提示工程可以用于各种任务,从回答问题到算术推理乃至各种应用领…...

Servlet的部署与安全
1 Servlet 部署 Servlet规范关于各个东西该放在哪里有许多严格的规则。 1.1 WAR war文件代表Web归档(Web Archive),war实际就是一个JAR,只不过扩展名是.war而不是.jar。 其采用了一种可移植的压缩形式,把整个Web应用结构(去掉…...
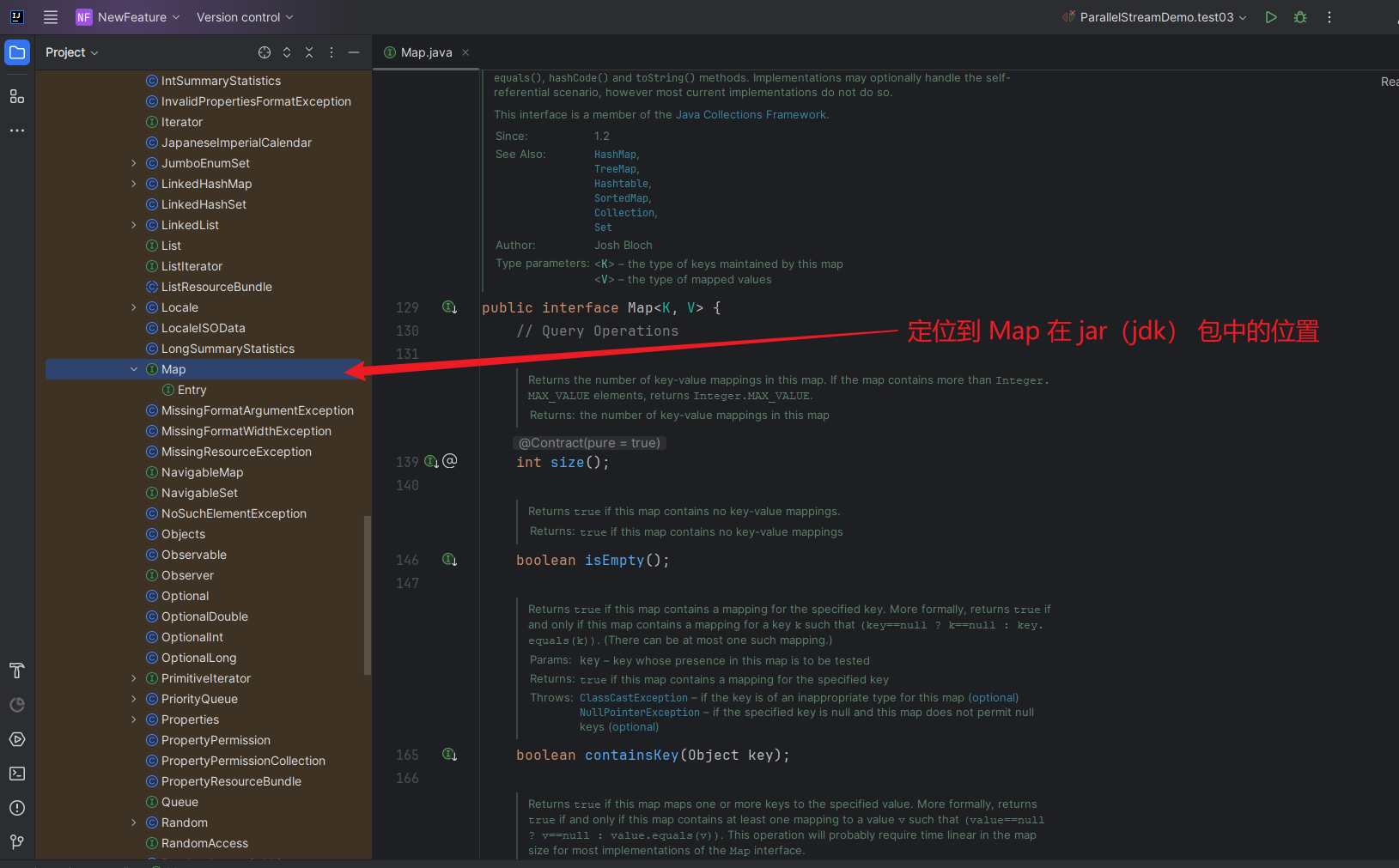
2023版IDEA的下载、安装、配置、快捷键、模板、插件与使用
🎉 为什么会有这篇教程:熟悉 IDEA 并能灵活熟练使用 IDEA 能极大提高您的开发效率!!! 📍 本文教程基于当前 idea 的最新版本 2023.2.2。 📍 本文教程的所有操作图片均是实操测试截图或 gif 动态…...

vue cli和vite区别
1.Vue CLI脚手架 什么是Vue脚手架? 在真实开发中我们不可能每一个项目从头来完成所有的webpack配置,这样显示开发的效率会大大的降低;所以在真实开发中,我们通常会使用脚手架来创建一个项目,Vue的项目我们使用的就是…...
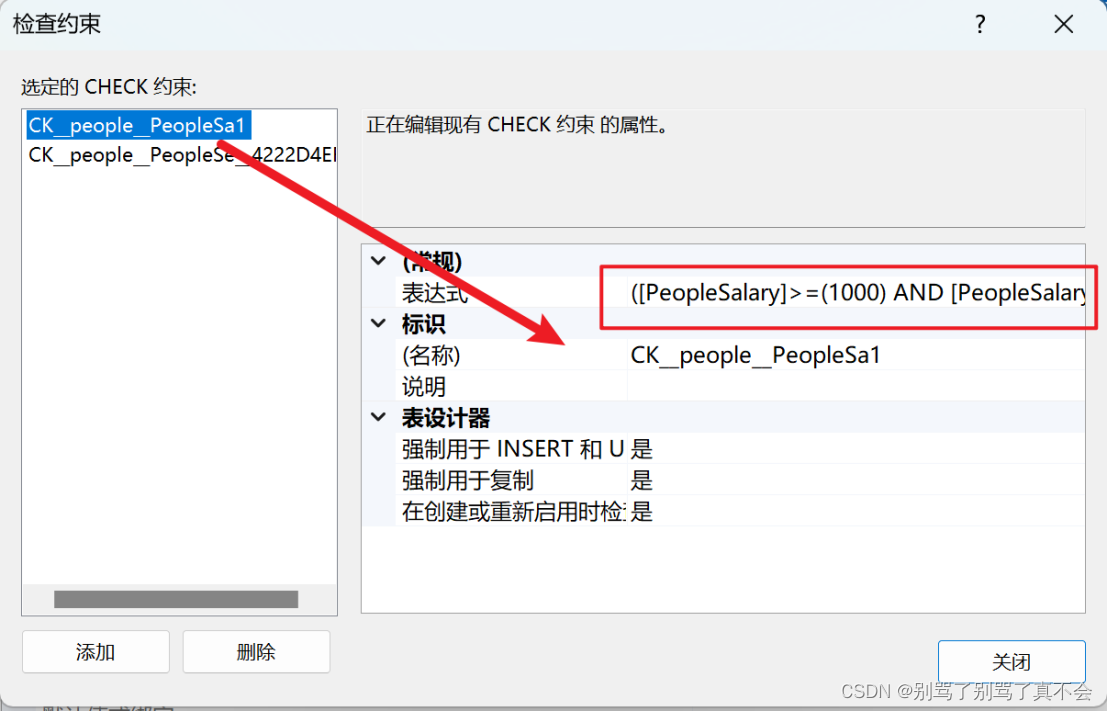
SQL Server修改表结构
在SQL Server中修改的关键字是 ALTER(改变;(使)更改;修改(衣服使更合身);改动) 列操作 添加列 添加列操作 alter tabel 表名 add 列名 数据类型--给员工表添加一个邮箱 alter的翻译是(改变) alter table people add PeopleMail varchar(2…...
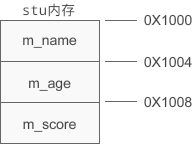
C++学习——对象的内存模型
以下内容源于C语言中文网的学习与整理,非原创,如有侵权请告知删除。 对象被创建时会在栈区或者堆区分配内存。我们直观的认识是,如果创建了 10 个对象,就要分别为这 10 个对象的成员变量和成员函数分配内存,如下图所示…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...
