华为OD机考算法题:找终点
目录
题目部分
解读与分析
代码实现
题目部分
| 题目 | 找终点 |
| 难度 | 易 |
| 题目说明 | 给定一个正整数数组,设为nums,最大为100个成员,求从第一个成员开始,正好走到数组最后一个成员,所使用的最少步骤数。 要求: 1.第一步必须从第一元素开始,且 1 <= 第一步的步长 < len/2; (说明:len为数组的长度,需要自行解析。) 2.从第二步开始,只能以所在成员的数字走相应的步数,不能多也不能少,如果目标不可达返回-1,只输出最少的步骤数量。 3.只能向数组的尾部走,不能往回走。 |
| 输入描述 | 由正整数组成的数组,以空格分隔,数组长度小于100,请自行解析数据数量。 |
| 输出描述 | 正整数,表示最少的步数,如果不存在输出-1。 |
| 补充说明 | 补充说明 |
| ------------------------------------------------------ | |
| 示例 | |
| 示例1 | |
| 输入 | 7 5 9 4 2 6 8 3 5 4 3 9 |
| 输出 | 2 |
| 说明 | 第一步:第一个选择步长 2,从第一个成员开始走 2 步,到达 9; 第二步:从 9 开始,经过自身数字 9 对应的 9 个成员到最后。 |
| 示例2 | |
| 输入 | 1 2 3 7 1 5 9 3 2 1 |
| 输出 | -1 |
| 说明 | 无 |
解读与分析
题目解读:
整形数组的长度为 len,第一步的大小可以是 [1, len/2) 中的任意一个数字,第二步和第二步以后的步数只能为当前成员的数字。
分析与思路:
题目中,第一步是可选的数字,一旦第一步数字固定了,后面的所有步数都是固定的。所以,此题可变的是第一步的步数,我们可以尝试第一步所有的可能的步数,计算所有能到达最后的步数,输出这些步数中的最小值即可。如果第一步尝试了所有可能的步数,全都无法达到最后一步,则输出 -1。
以上方法的时间复杂度为O()。
代码实现
Java代码
import java.util.Scanner;/*** 篮球比赛* @since 2023.10.08* @version 0.1* @author Frank**/
public class FindEnd {public static void main(String[] args) {Scanner sc = new Scanner(System.in);while (sc.hasNext()) {String input = sc.nextLine();String[] numbersStr = input.split( " " );processFindEnd( numbersStr );}}private static void processFindEnd( String numbersStr[] ){int count = numbersStr.length;int[] numbers = new int[count];for( int i = 0; i < count; i ++ ){numbers[i] = Integer.parseInt( numbersStr[i] );}int minSteps = Integer.MAX_VALUE;for( int i = 1; i < count * 1.0 / 2; i ++ ){int steps = 1;int next = i;while( next < count -1 ){steps ++;next = next + numbers[next];if( next == count -1 ){if( steps < minSteps ){minSteps = steps;} break;}}}if( minSteps == Integer.MAX_VALUE ){minSteps = -1;}System.out.println( minSteps );}}JavaScript代码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void async function() {while (line = await readline()) {var numberArr = line.split(" ");processFindEnd(numberArr);}
}();function processFindEnd(numbersStr) {var count = numbersStr.length;var numbers = new Array();for (var i = 0; i < count; i++) {numbers[i] = parseInt(numbersStr[i]);}var minSteps = Number.MAX_VALUE;for (var i = 1; i < count / 2; i++) {var steps = 1;var next = i;while (next < count - 1) {steps++;next = next + numbers[next];if (next == count - 1) {if (steps < minSteps) {minSteps = steps;}break;}}}if (minSteps == Number.MAX_VALUE) {minSteps = -1;}console.log(minSteps);
}(完)
相关文章:
华为OD机考算法题:找终点
目录 题目部分 解读与分析 代码实现 题目部分 题目找终点难度易题目说明给定一个正整数数组,设为nums,最大为100个成员,求从第一个成员开始,正好走到数组最后一个成员,所使用的最少步骤数。 要求: 1.第…...

el-table通过scope.row获取表格每列的值,以及scope.$index
<el-table-column type"selection" width"55"></el-table-column><el-table-column prop"id" label"ID" width"80"></el-table-column><el-table-column prop"name" label"文件名…...

uni-app:本地缓存的使用
uni-app 提供了多种方法用于本地缓存的操作。下面是一些常用的 uni-app 本地缓存方法: uni.setStorageSync(key, data): 同步方式将数据存储到本地缓存中,可以使用对应的 key 来获取该数据。 uni.setStorage({key, data}): 异步方式将数据存储到本地缓存…...
在Scrum敏捷开发中,开发人员(Developers)的职责
在Scrum敏捷开发中,开发人员(Developers)是Scrum团队中最重要的角色之一,负责产品的开发和交付,其重要性不言而喻。 那开发人员的职责和需要参加的活动是什么呢? Developers核心职责: 承诺并完…...
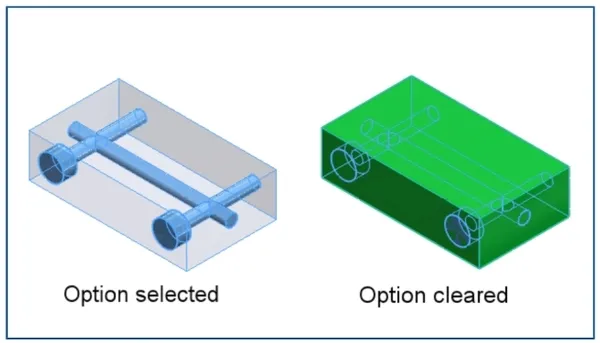
SOLIDWORKS® 2024 新功能 - 3D CAD
1、 先前版本的兼容性 • 利用您订阅的 SOLIDWORKS,可将您的 SOLIDWORKS 设计作品保存为旧版本,与使用旧版本 SOLIDWORKS 的供应商无缝协作。 • 可将零件、装配体和工程图保存为新版本前两年之内的SOLIDWORKS 版本。 优点: 即使其他用户正…...

系统架构设计:20 论软件需求管理
目录 一 需求工程 1 需求开发 1.1 需求获取 1.1.1 软件需求的分类 1.1.2 需求获取方法...
)
K8S云计算系列-(2)
1.Kubernetes平台配置实战 部署Kubernetes云计算平台,至少准备两台服务器,服务器CPU至少2C,内存4G,环境如下所示: Kubernetes Master节点:192.168.1.146 Kubernetes Minion节点:192.168.1.147…...
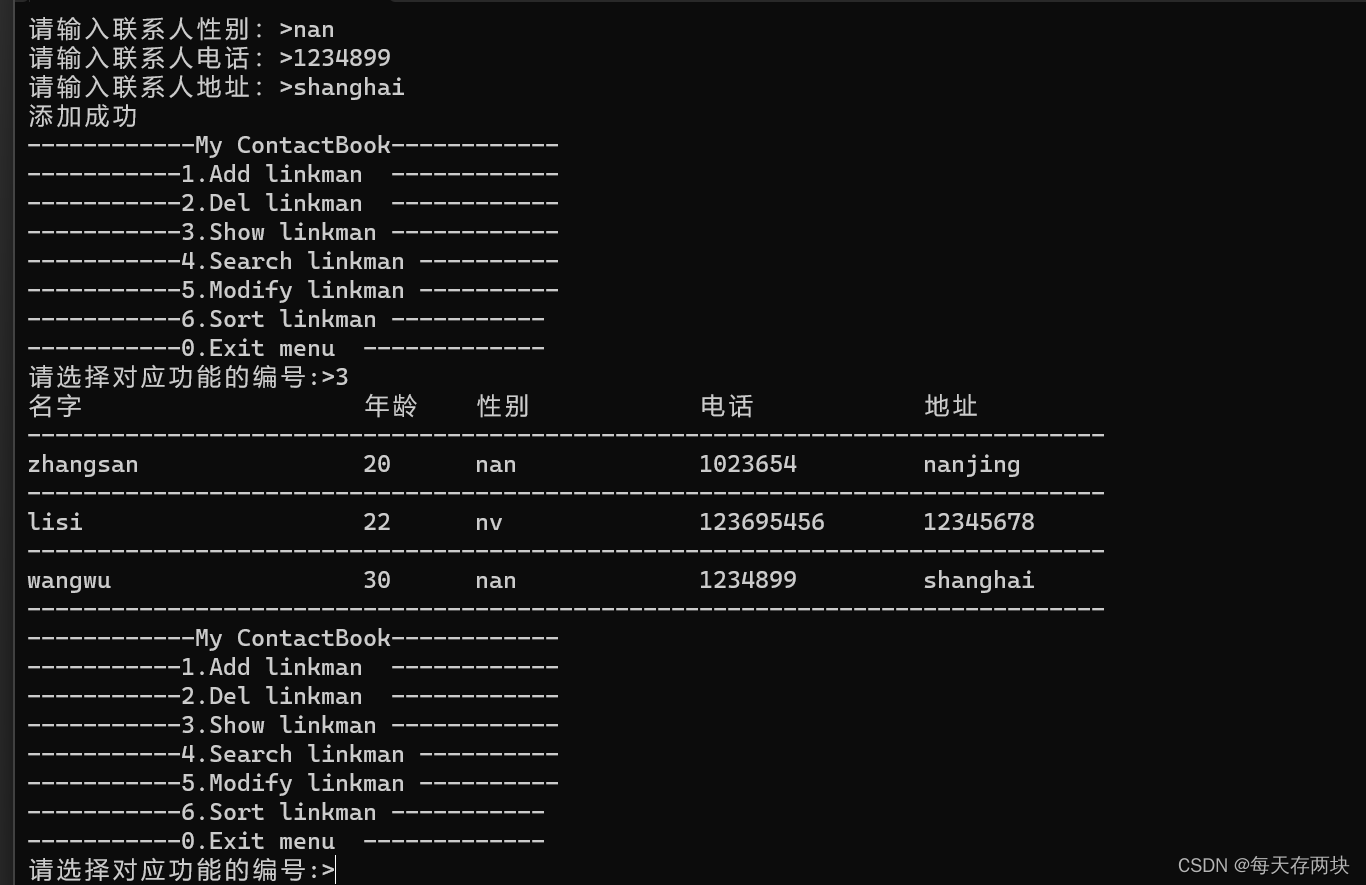
通讯录(C语言版)
用c语言实现一个通讯录 功能:.添加、删除、查找、更改、显示、排序联系人 内存存储方式:结构体数组 1.打印菜单,各个功能分别用函数实现,将函数声明放在头文件中。 2.定义联系人信息,将联系人信息与countÿ…...
natapp内网穿透-将本地运行的程序/服务器通过公网IP供其它人访问
文章目录 1.几个基本概念1.1 局域网1.2 内网1.3 内网穿透1.4 Natapp 2.搭建内网穿透环境3.本地服务测试 1.几个基本概念 1.1 局域网 LAN(Local Area Network,局域网)是一个可连接住宅,学校,实验室,大学校…...

数据结构八大排序Java源码
文章目录 [1]. 堆排序[2]. 冒泡排序[3]. 选择排序[4]. (直接)插入排序[5]. 希尔排序(属于插入算法)[6]. 快速排序[7]. 归并排序[8]. 基数排序 王道数据结构排序讲解 排序算法最佳时间复杂度最坏时间复杂度平均时间复杂度空间复杂度…...
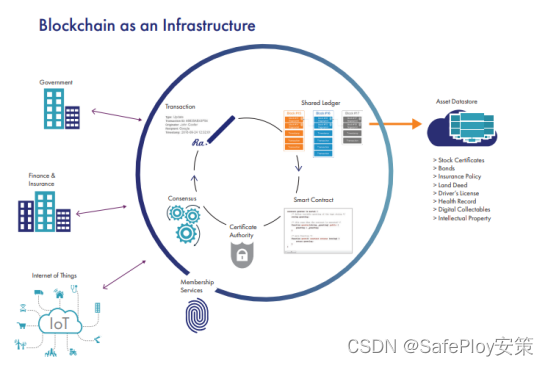
区块链加密虚拟货币交易平台安全解决方案
区块链机密货币交易锁遭入侵,安全存在隐患。使用泰雷兹Protect server HSM加密机,多方位保护您的数据,并通过集中化管理,安全的存储密钥。 引文部分: 损失7000万美元!黑客入侵香港区块链加密货币交易所 2023年9月&…...
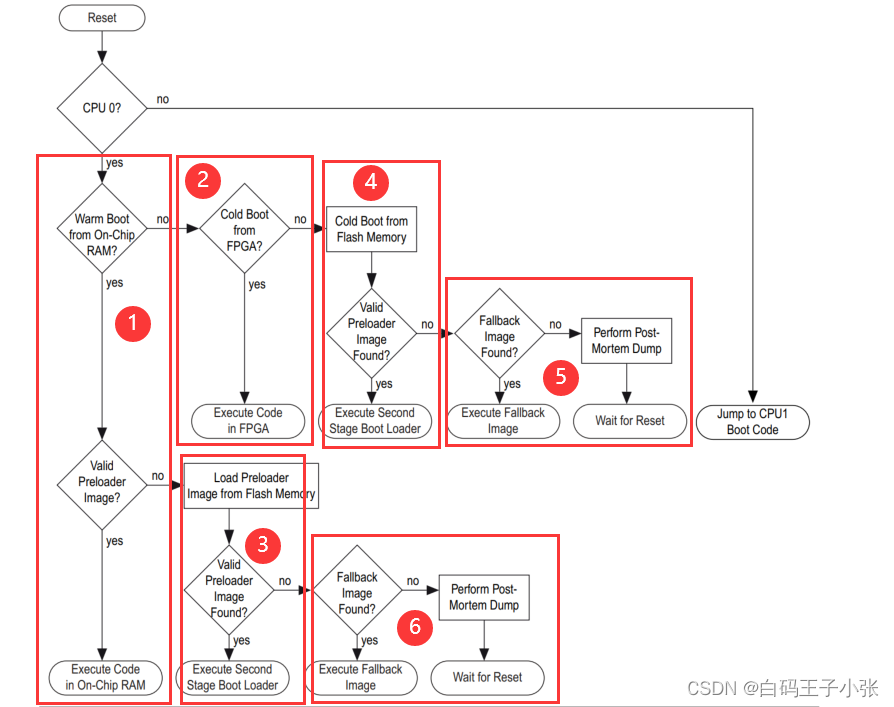
【SoC FPGA】HPS启动过程
SoC HPS启动流程 Boot ROMPreloaderBoot Loader HPS的启动是一个多阶段的过程,每一个阶段都会完成对应的工作并且将下一个阶段的执行代码引导起来。每个阶段均负责加载下一个阶段。第一个软件阶段是引导 ROM,引导 ROM 代码查找并且执行称为预加载器的第 …...

Wireshark CLI | Mergecap 篇
简介 Mergecap 是 Wireshark 程序安装时附带的可选工具之一,用于合并数据包文件的命令行工具。 mergecap [ -a ] [ -F <file format> ] [ -I <IDB merge mode> ] [ -s <snaplen> ] [ -V ] -w <outfile>|- <infile> [<infile>…...
10个打工人必备AI神器,升职加薪靠AI
HI,同学们,我是赤辰,本期是第18篇AI工具类教程,文章底部准备了粉丝福利,看完后可领取!1. Runway(文字转视频AI工具) 只需要一句提示词就能精确生成你所想象的视频场景,还…...

Java架构师缓存架构设计
目录 1 导学2 高性能概述2.1 高性能的定义和衡量指标2.2 如何实现高性能的计算机系统或软件程序2.3 木桶理论2.4 如何实现计算机系统或软件程序的高性能3 多级缓存设计3.1 浏览器缓存3.2 CDN缓存3.3 负载均衡的缓存3.4 进程内缓存3.5 分布式缓存4 缓存技术方案5 如何进行缓存拆…...

Linux 安全 - DAC机制
文章目录 一、安全简介二、DAC2.1 UNIX 的自主访问控制2.2 Linux 的自主访问控制 三、进程凭证3.1 简介3.2 uid/gid3.3 系统调用 四、客体标记4.1 简介4.2 系统调用 五、UGO规则源码分析参考资料 一、安全简介 计算机系统应对安全挑战的办法大致有四种:隔离、控制、…...

解决Windows系统win+shift+s截图快捷键失效问题
文章目录 打开任务管理器找到Windows资源管理器,选择重新启动 打开任务管理器 按“Win R”打开: 输入taskmgr.exe,运行,即可打开任务管理器: 找到Windows资源管理器,选择重新启动 点击右下角的“重新启…...
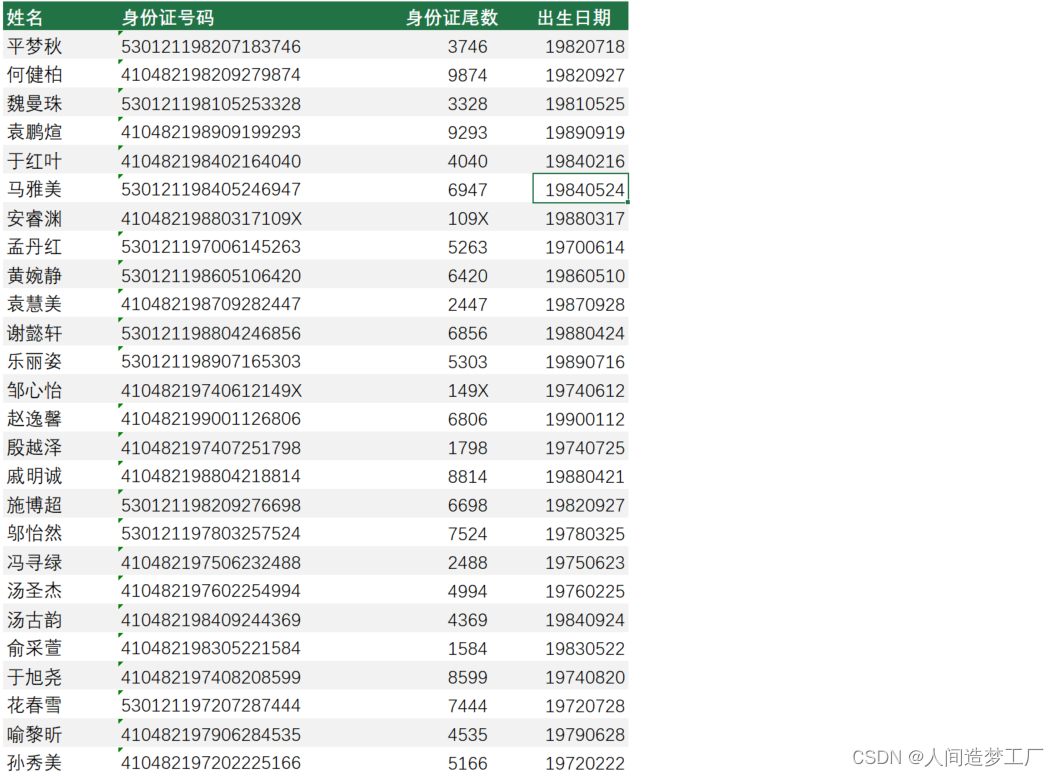
Excel 快速填充
文章目录 利用快速填充进行提取数据利用快速填充进行拆分重组 2013 及以上版本才有的功能. 利用快速填充进行提取数据 有一列的数据已有, 需要提取部分数据到另一列, 只需要输入部分内容, 后面内容可以自动显示, 按下回车即可快速填充. 只要前面手动输入的内容没有错得太离谱…...

OPENCV图像和视频处理
图像基本操作: Opencv图像处理(全)_胖墩会武术的博客-CSDN博客 import cv2 import matplotlib.pyplot as plt import numpy as npimgcv2.imread(1.jpg) #图像的显示 cv2.imshow(image,img) cv2.waitKey(0) …...
QDir实践
现在有多个文件,路径为: a\xxx\kmd_config\c.json 其中xxx是变量 startcalc,,,,,, 目标: 访问每一个json文件 实例: QString app_path QApplication::applicationDirPath() "/app";QDir dir(app_path);QStringLi…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
