【数据结构】归并排序和计数排序(排序的总结)
目录
一,归并排序的递归
二,归并排序的非递归
三,计数排序
四,排序算法的综合分析
一,归并排序的递归
基本思想:
归并采用的是分治思想,是分治法的一个经典的运用。该算法先将原数据进行拆分,此步骤与二叉树的拆分思想一样(因此,运用递归比较简单),然后将最终拆分后的每一小部分排序,最后将已有序的子序列进行合并,得到完全有序的序列,其中关键为要使每个分割后的子序列有序,再使子序列段间有序,即合并有序序列。以上中将两个有序表合并成一个有序表称为二路归并。思想图如下(以升序为例):
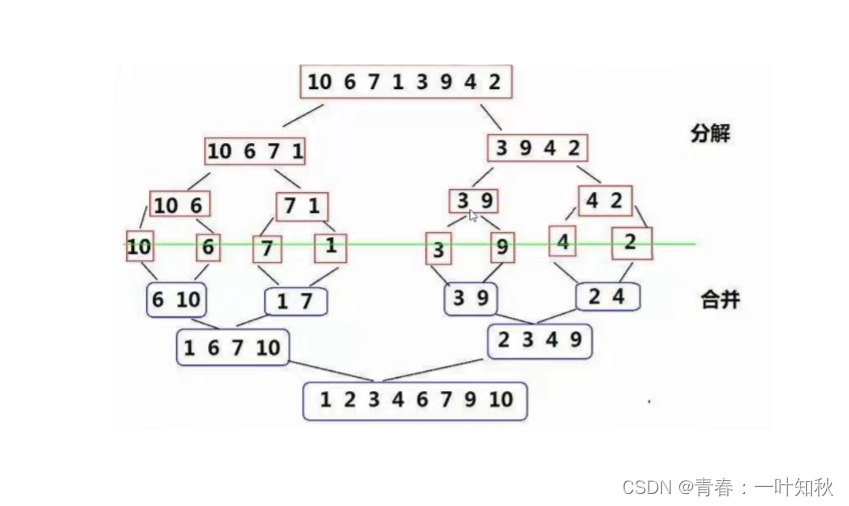
上图中,先以中间数据为界,将一堆数据进行不断分解,当分解完全后,再进行合并,而在合并时其实就是边排序边合并。由于在排序中要改动原数据,因此,我们可再创建一个数组进行改动,然后将改动后的数据赋值给原数据块即可,代码和导图如下:
代码运行导图
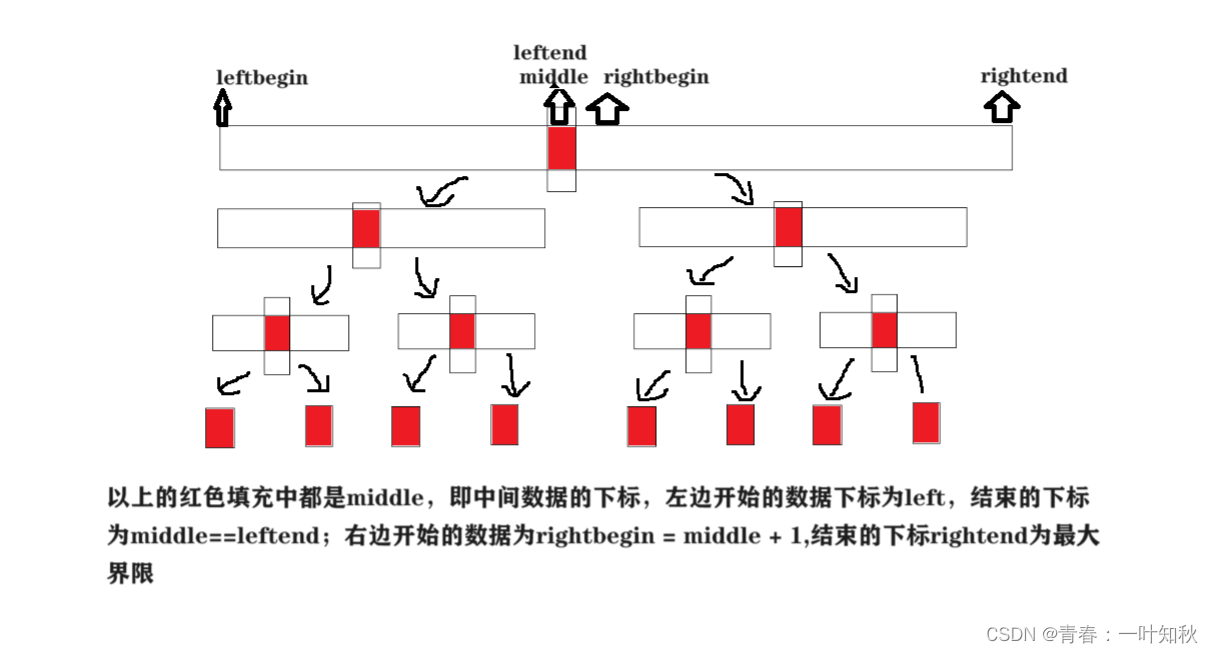
导图中,先取中间值,以此下标为界限分开左右区间,然后再不断递归分割,最后一次分割为leftbegin == leftend,rightbegin == rightend,此时就要进行排序组合,组合完子序列后即可往原序列就行赋值,此为一趟遍历,然后递归就不断进行返回,即不断就行合并排序,最终全部元素有序。
归并代码:
void MergeFunction(int* a, int* nums, int n, int begin, int end) {
//当分割区间为1个数据时就要停止分割,即此时begin == end
if (begin == end) {
return;
}
int middle = (begin + end) / 2;//中间数据,控制界限
//在左区间[begin, middle]和右区间[middle + 1, end]进行不断分割
MergeFunction(a, nums, n, begin, middle);
MergeFunction(a, nums, n, middle + 1, end);
//分割后,下面是进行左右区间的排序
int leftbegin = begin, leftend = middle;
int rightbegin = middle + 1, rightend = end;
int insert = begin;
//以下是进行分割后的排序
while (leftbegin <= leftend && rightbegin <= rightend) {
if (a[leftbegin] < a[rightbegin]) {
nums[insert++] = a[leftbegin++];
}
else {
nums[insert++] = a[rightbegin++];
}
}
while (leftbegin <= leftend) {
nums[insert++] = a[leftbegin++];
}
while (rightbegin <= rightend) {
nums[insert++] = a[rightbegin++];
}
//拷贝数组
memcpy(a + begin, nums + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n) {
int* nums = (int*)malloc(sizeof(int) * n);//此数组用于临时放入数据
if (!nums) {
perror("nums malloc");
exit(-1);
}
MergeFunction(a, nums, n, 0, n - 1);
free(nums);
}
样例代码,将以下中数组a进行排序(升序):
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void MergeFunction(int* a, int* nums, int n, int begin, int end) {//当分割为1个时就要停止分割,即此时begin == endif (begin == end) {return;}int middle = (begin + end) / 2;//中间数据,控制界限//在左区间[begin, middle]和右区间[middle + 1, end]进行不断分割MergeFunction(a, nums, n, begin, middle);MergeFunction(a, nums, n, middle + 1, end);//分割后,下面是进行左右区间的排序int leftbegin = begin, leftend = middle;int rightbegin = middle + 1, rightend = end;int insert = begin;//以下是进行分割后的排序while (leftbegin <= leftend && rightbegin <= rightend) {if (a[leftbegin] < a[rightbegin]) {nums[insert++] = a[leftbegin++];}else {nums[insert++] = a[rightbegin++];}}while (leftbegin <= leftend) {nums[insert++] = a[leftbegin++];}while (rightbegin <= rightend) {nums[insert++] = a[rightbegin++];}//拷贝数组memcpy(a + begin, nums + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n) {int* nums = (int*)malloc(sizeof(int) * n);//此数组用于临时放入数据if (!nums) {perror("nums malloc");exit(-1);}MergeFunction(a, nums, n, 0, n - 1);free(nums);
}
int main() {int a[] = { 10,6,7,1,3,9,4,2 };MergeSort(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); i++) {fprintf(stdout, "%d ", a[i]);}puts("");return 0;
}运行图:
二,归并排序的非递归
我们平常将递归改成非递归首先可能想起要运用栈结构,但是,我们先理一下归并的思路,当我们不断分割时确实可以用栈结构来控制区间,但是当回并时可能就比较麻烦,因此,本人不建议用栈结构,不是不可以,是有更好的方法。
归并递归时是将数据不断进行二分,即分治思想,当用非递归时,我们可设置一个间隔gap,以次模仿递归时的二分思想,每次循环结束后将此间隔乘二即可。非递归思路导图如下:
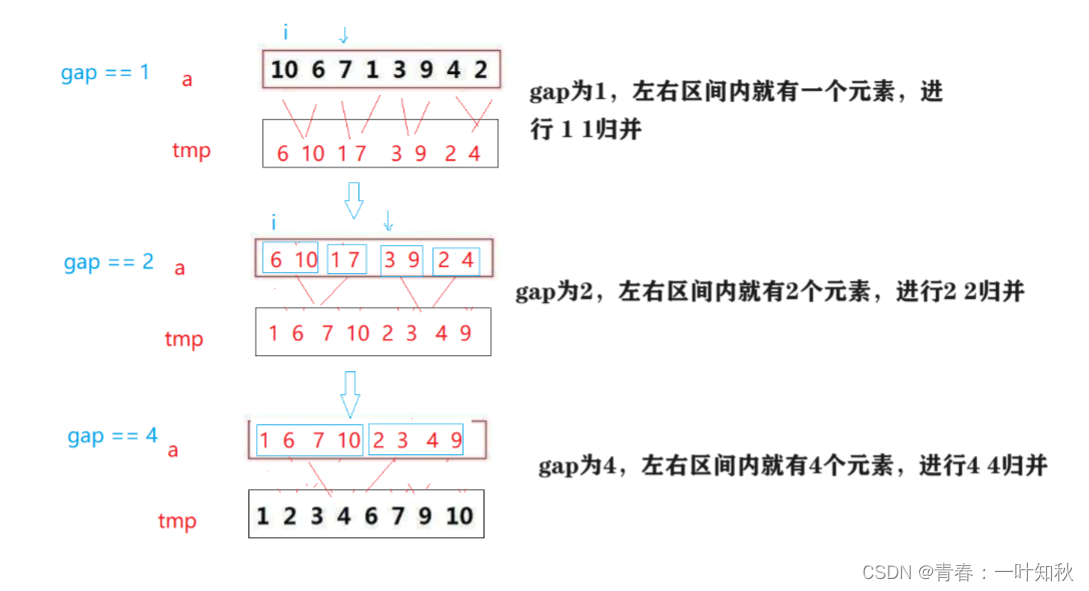
由以上图不难发现,此种非递归合并的思路与递归合并的思路有些不太一样,此种非递归的思想是一旦有了一个间隔值后,就一次性的将全部数据按照此间隔值进行间隔归并。
非递归归并的时候要注意一个点,当数据个数为奇数时,不难发现,左区间[leftbegin,leftend]无影响,但右区间[rightbegin,rightend]将会溢出,此时情况,如果rightbegin溢出的话那么可之间退出,因为据上图中所示,每一趟归并时就相当于将下一趟的左区间就排列有序了;如果rightend溢出的话,直接令rightend为最后一个元素的下标进行归并排序即可。当数据个数为偶数时不会出现溢出情况。
代码如下:
void MergeSortNonR(int* a, int n) {
int* nums = (int*)malloc(sizeof(int) * n);
//gap是每次隔离的间隔,也可理解为将要排序的元素个数
int gap = 1;//控制gap间据的大小
while (gap < n) {
for (int i = 0; i < n; i += 2 * gap) {
//以gap为间距分割,左区间[leftbegin,leftend]共有gap个元素
int leftbegin = i, leftend = i + gap - 1;
//以gap为间距分割,当原始数有偶数的元素时,右区间[rightbegin,rightend]有gap个元素
int rightbegin = i + gap, rightend = i + gap + gap - 1;
int insert = i;
//以下是当元素个数为奇数时的情况
if (rightbegin >= n) {
break;
}
if (rightend >= n) {
rightend = n - 1;
}
//开始进行排序,排列的数据区间为[leftbegin, rightend]
while (leftbegin <= leftend && rightbegin <= rightend) {
if (a[leftbegin] < a[rightbegin]) {
nums[insert++] = a[leftbegin++];
}
else {
nums[insert++] = a[rightbegin++];
}
}
while (leftbegin <= leftend) {
nums[insert++] = a[leftbegin++];
}
while (rightbegin <= rightend) {
nums[insert++] = a[rightbegin++];
}
//将排列的区间[leftbegin, rightend]进行拷贝,因为leftbegin和rightbegin都已改变,所以不能用这两个数据
memcpy(a + i, nums + i, sizeof(int) * (rightend - i + 1));
}
gap *= 2;
}
free(nums);
}
样例代码,将以下中数组a进行排序(升序):
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void MergeSortNonR(int* a, int n) {int* nums = (int*)malloc(sizeof(int) * n);//gap是每次隔离的间隔,也可理解为将要排序的元素个数int gap = 1;while (gap < n) {for (int i = 0; i < n; i += 2 * gap) {//leftbegin和leftend理解为在gap区间内的元素int leftbegin = i, leftend = i + gap - 1;//rightbegin和rightend可理解为在预排序gap区间的后面的元素int rightbegin = i + gap, rightend = i + gap + gap - 1;int insert = i;//以下是当元素为奇数时的情况if (rightbegin >= n) {break;}if (rightend >= n) {rightend = n - 1;}//开始进行排序,排列的数据区间为[leftbegin, rightend]while (leftbegin <= leftend && rightbegin <= rightend) {if (a[leftbegin] < a[rightbegin]) {nums[insert++] = a[leftbegin++];}else {nums[insert++] = a[rightbegin++];}}while (leftbegin <= leftend) {nums[insert++] = a[leftbegin++];}while (rightbegin <= rightend) {nums[insert++] = a[rightbegin++];}//将排列的区间[leftbegin, rightend]进行拷贝,因为leftbegin和rightbegin都以改变,所以不能用这两个数据memcpy(a + i, nums + i, sizeof(int) * (rightend - i + 1));}gap *= 2;}free(nums);
}
int main() {int a[] = { 10,6,7,1,3,9,4,2 };MergeSortNonR(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); i++) {fprintf(stdout, "%d ", a[i]);}puts("");return 0;
}运行图:
运算发的效率:
最后我们来谈论一下此算法的效率,不难发现,由于此算法中运用的是二分思想,所以时间复杂度为O(nlogn),空间复杂度O(n)。由此可见,此算法的效率也算高,跟快排不同的是,此算法与原始数据的初始位置并无太大影响,效率比较稳定。
三,计数排序
计数排序可从字面意思理解,通过数组的下标来计数来间接实现数据的排序。首先,我们需设置一个数组,此数组是通过下标来进行计数的,原数据中最大数据个数为max - min + 1(max是原数据的最大元素,min是原数据最小的元素),即幅度range在区间[0,max - min]中,因此,我们可设置数组大小为max - min + 1(不包括重复数组,重复的数据我们可用相同下标对应的数值记录出现的次数),即最大下标为max - min(记录最大元素的位置),下标的设置思想为:原数据 - min。然后将设置数组初始化为0(也可选举其它值,但选举0是最为简单的),0表示原数据中没有此元素,然后幅度range遍历,一旦存在此元素加1,表示出现元素的次数,最后将其设置数组中出现过元素的下标加上min赋给原数据即可得到有序序列,思维导图如下:

代码如下(以升序为例):
void CountSort(int* a, int n) {
//以下是寻找最大值max和最小值min,为了后面确定幅度range
int min = a[0], max = a[n - 1], j = 0;
for (int i = 0; i < n; i++) {
if (a[i] > max) {
max = a[i];
}
if (a[i] < min) {
min = a[i];
}
}
//最大元素个数为range,下标为“原数据 - min”
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
memset(count, 0, sizeof(int) * range);//初始化0,表元素个数为0
for (int i = 0; i < n; i++) {
//用计数数组count的有序下标来进行有序计数,记录出现过元素的次数
count[a[i] - min]++;//注意: 不能count[a[i] - min] = 1,因为可能有重复数据
}
//最后遍历,一旦存在此值将,下标 + min即为数据
for (int i = 0; i < range; i++) {
while (count[i]--) {
a[j++] = i + min;
}
}
free(count);
}
代码演示(以升序为例):
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void CountSort(int* a, int n) {//以下是寻找最大值max和最小值min,为了后面确定幅度rangeint min = a[0], max = a[n - 1], j = 0;for (int i = 0; i < n; i++) {if (a[i] > max) {max = a[i];}if (a[i] < min) {min = a[i];}}//最大元素个数为range,下标为“原数据 - min”int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);memset(count, 0, sizeof(int) * range);//初始化0,表元素个数为0for (int i = 0; i < n; i++) {//用计数数组count的有序下标来进行有序计数,记录出现过元素的次数count[a[i] - min]++;//注意: 不能count[a[i] - min] = 1,因为可能有重复数据}//最后遍历,一旦存在此值将,下标 + min即为数据for (int i = 0; i < range; i++) {while (count[i]--) {a[j++] = i + min;}}free(count);
}
int main() {int a[] = { 10,6,7,1,3,9,4,2 };CountSort(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); i++) {fprintf(stdout, "%d ", a[i]);}puts("");return 0;
}运行图:

计数效率与注意要点:
计数排序的时间复杂度为O(range + n) ,空间复杂度为O(range),效率是非常高的,因为无论什么排序算法,最好的时间效率无非是O(n),而计数排序的时间复杂度达到O(range + n),已经非常接近O(n)。无论是希尔排序,堆排序,快速排序还是归并排序都达不到此效率,但此算法也不是最优选择,因为此算法完全可以说是那空间换时间,当range非常大时会消耗很大的空间,而且由于此算法是运用数组下标进行间接排序的,因此,此算法只能对整型排序,不能对其它数据类型进行排序,使得此算法有了很大的局限性。
四,排序算法的综合分析
1,算法的效率分析
排序算法的效率不能只根据时间复杂度和空间复杂度,因为两者的计算都是取最好情况和最坏情况进行概率的综合分析,最终取平均,比如排序的原始序列不同,快排算法,直接插入算法和冒泡算法的效率比较大,直接插入和冒泡最好的情况都是有序的情况,此时时间复杂度都为O(n),而快排最好的情况是基准值每次在中间,此时时间复杂度为O(nlogn)。但大多数情况下,我们根本预测不了原始序列和原始数据,所以在大多数情况下可直接根据时间复杂度和空间复杂度直接判断,若对数据比较敏感的话就要根据具体情况进行具体分析,从而选取最优算法。
2,算法的稳定性
稳定性:相同的数据排序后,相对位置是否发生变化,若两者之间的相对位置没有发生变化,则算法稳定,发生变化,算法不稳定。
在初学情况下,稳定性确实不算太重要,但是在后面深入学习系统操作和程序等先后顺序就显得尤为重要,例如,一个程序要对学生进行考试排名,其中高成绩出现了两个99分的和两个98分,这时两个99分的学生谁先排入第一名和两个98分的学生谁排入第三名就显得尤为重要,这就要求排序算法的稳定性。最后总结一下各个算法的效率和稳定性:
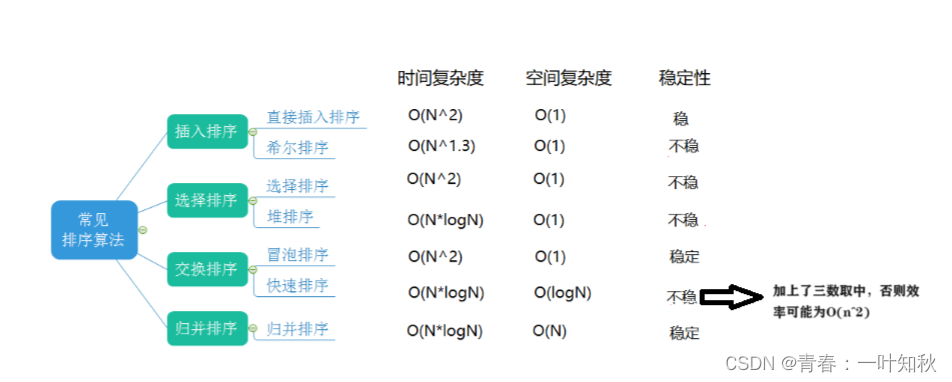
其中计数排序没必要加上,因为计数局限性太强了,在后面的学习中基本用不到,并且提醒一下,以上中的算法效率和稳定性千万不要死记,因为之前说过,这些算法的效率基本都不稳定,不同的情况可能出现不同的效率,而某些算法的设计不同可能稳定,也可能不稳定,因此,理解算法的思想和如何实现尤为重要。
相关文章:

【数据结构】归并排序和计数排序(排序的总结)
目录 一,归并排序的递归 二,归并排序的非递归 三,计数排序 四,排序算法的综合分析 一,归并排序的递归 基本思想: 归并采用的是分治思想,是分治法的一个经典的运用。该算法先将原数据进行拆…...

某医疗机构:建立S-SDLC安全开发流程,保障医疗前沿科技应用高质量发展
某医疗机构是头部资本集团旗下专注大健康领域战略性投资与运营的实业公司,市场规模超300亿。该医疗机构已完成数字赋能,形成了标准化、专业化、数字化的疾病和健康管理体系,将进一步规划战略方向,为人工智能纳米技术、高温超导、生…...

验证二叉搜索树的后序遍历序列
LCR 152. 验证二叉搜索树的后序遍历序列 class VerifyTreeOrder:"""LCR 152. 验证二叉搜索树的后序遍历序列https://leetcode.cn/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof/description/"""def solution(self, postorder: Lis…...
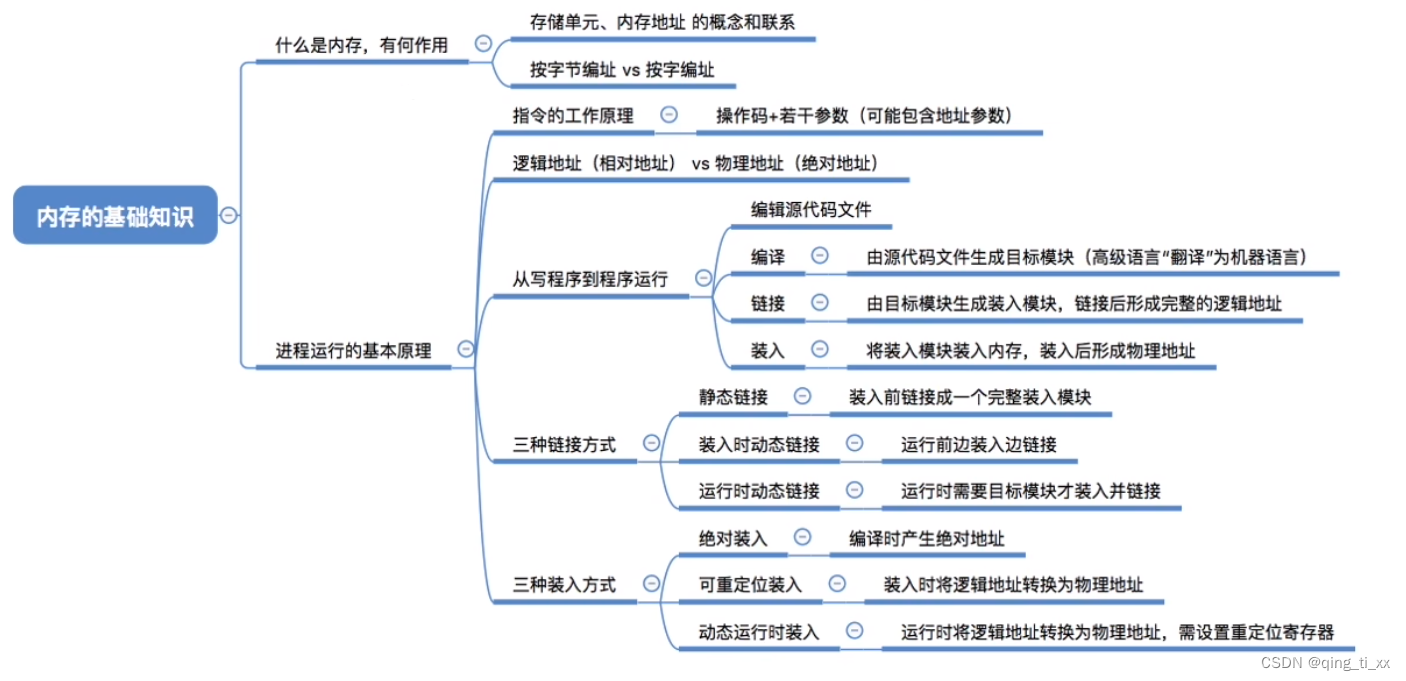
第三章 内存管理 一、内存的基础知识
目录 一、什么是内存 二、有何作用 三、常用数量单位 四、指令的工作原理 五、装入方式 1、绝对装入 2、可重定位装入(静态重定位) 3、动态运行时装入(动态重定位) 六、从写程序到程序运行 七、链接的三种方式 1、静态…...

【Java学习之道】Java常用集合框架
引言 在Java中,集合框架是一个非常重要的概念。它提供了一种方式,让你可以方便地存储和操作数据。Java中的集合框架包括各种集合类和接口,这些类和接口提供了不同的功能和特性。通过学习和掌握Java的集合框架,你可以更好地管理和…...
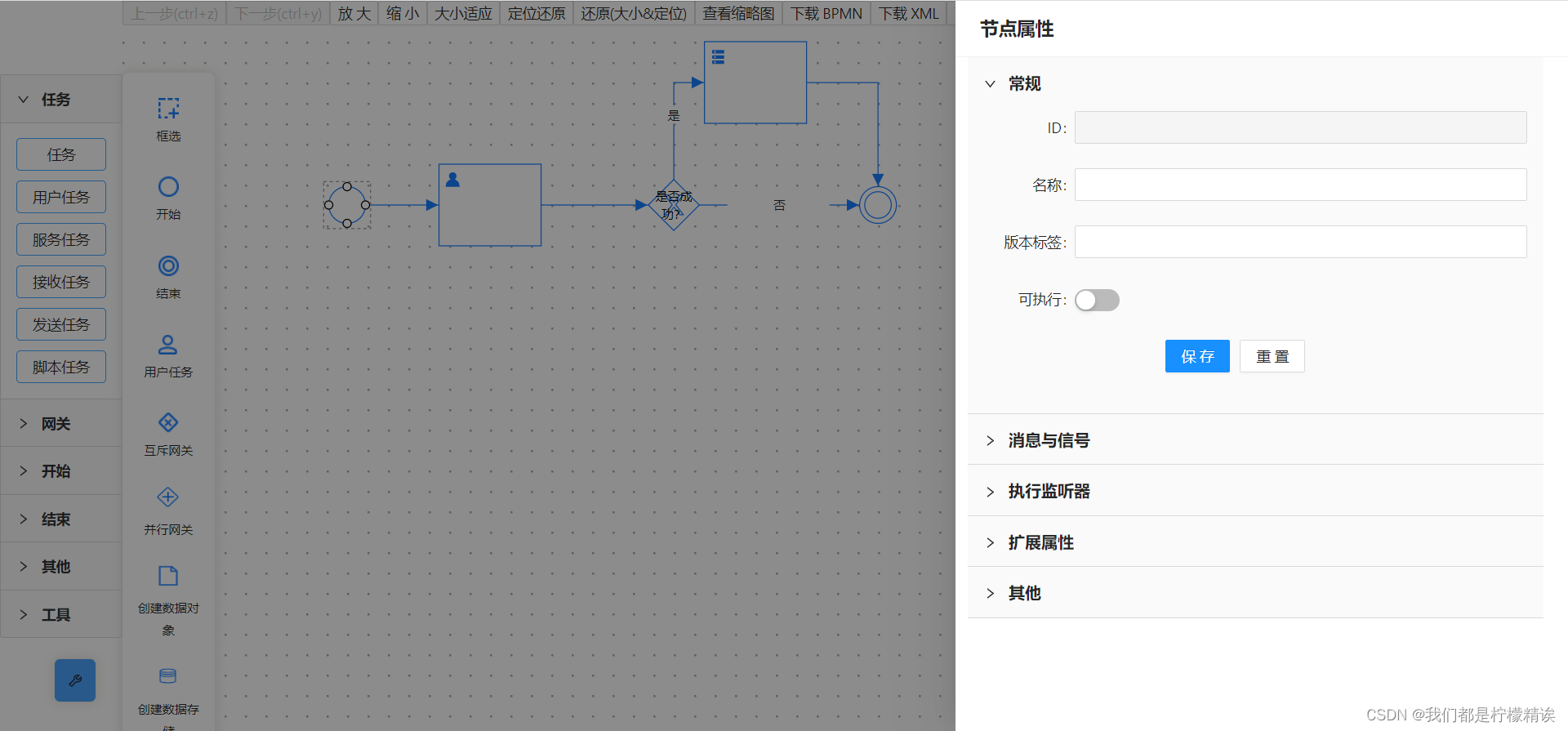
logicFlow 流程图编辑工具使用及开源地址
一、工具介绍 LogicFlow 是一款流程图编辑框架,提供了一系列流程图交互、编辑所必需的功能和灵活的节点自定义、插件等拓展机制。LogicFlow 支持前端研发自定义开发各种逻辑编排场景,如流程图、ER 图、BPMN 流程等。在工作审批配置、机器人逻辑编排、无…...
/OPTEE之动态代码分析汇总)
ATF(TF-A)/OPTEE之动态代码分析汇总
安全之安全(security)博客目录导读 1、ASAN(AddressSanitizer)地址消毒动态代码分析 2、ATF(TF-A)之UBSAN动态代码分析 3、OPTEE之KASAN地址消毒动态代码分析...

10-11 周三 shell xargs tr curl 做大事情
最近发现,shell的小工具非常的强大,简单记录下 tr命令 -d 删除字符串1中所有输入字符。-s 删除所有重复出现字符序列,只保留第一个;即将重复出现字符串压缩为一个字符串 -d 用于删除查询到的字符串中的空格。 [test3NH-DC-NM1…...

1.1 向量与线性组合
一、向量的基础知识 两个独立的数字 v 1 v_1 v1 和 v 2 v_2 v2,将它们配对可以产生一个二维向量 v \boldsymbol{v} v: 列向量 v v [ v 1 v 2 ] v 1 v 的第一个分量 v 2 v 的第二个分量 \textbf{列向量}\,\boldsymbol v\kern 10pt\boldsymbol …...

django: You may need to add ‘localhost‘ to ALLOWED_HOSTS
参考:https://blog.csdn.net/qq_21744873/article/details/87857279 python manage.py runserver后页面访问失败,提示: DisallowedHost at /admin/ Invalid HTTP_HOST header: ‘localhost:8000’. You may need to add ‘localhost’ to ALLOWED_HOSTS…...

网络安全(黑客技术)—自学手册
1.网络安全是什么 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 2.网络安全市场 一、是市场需求量高; 二、则是发展相对成熟…...
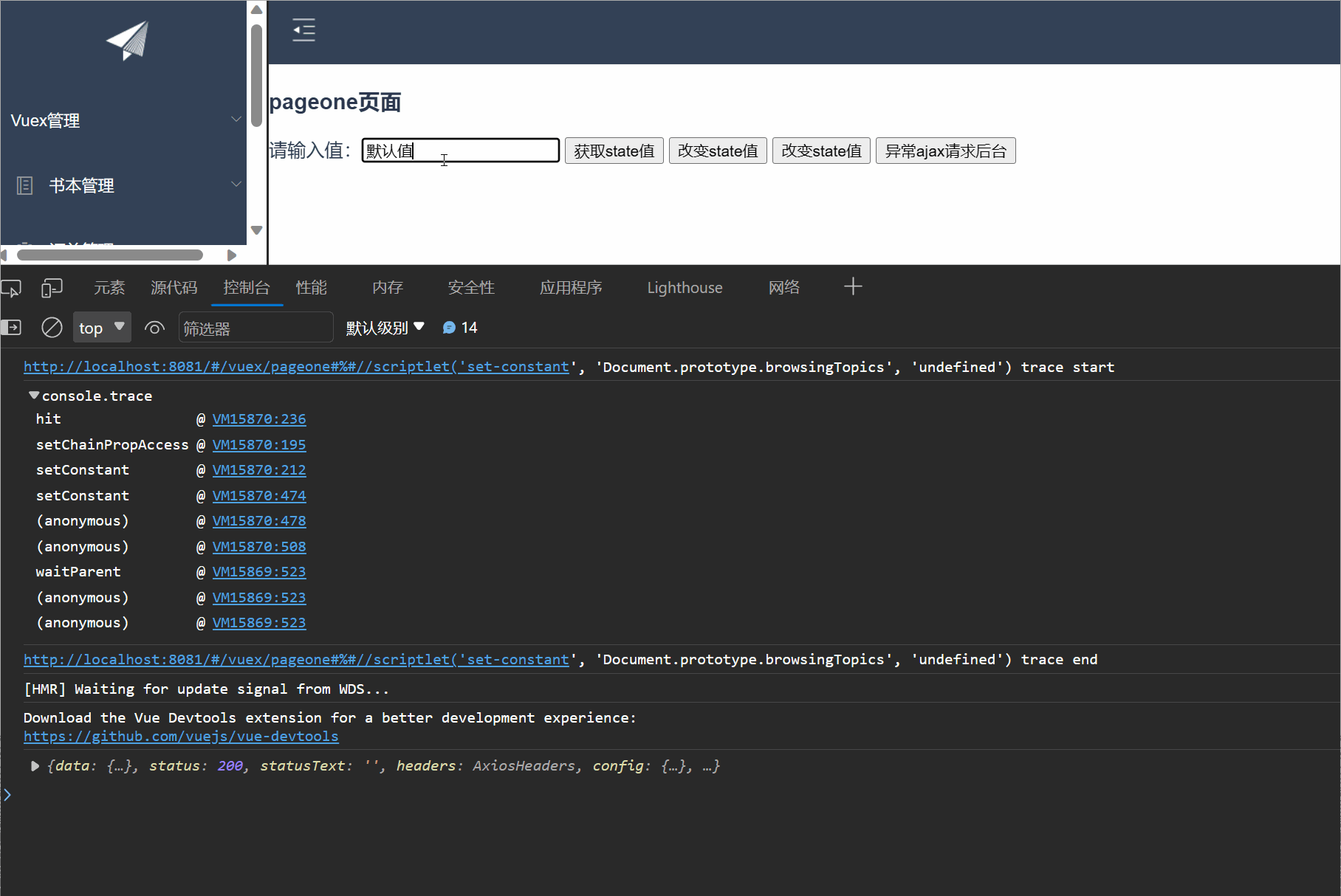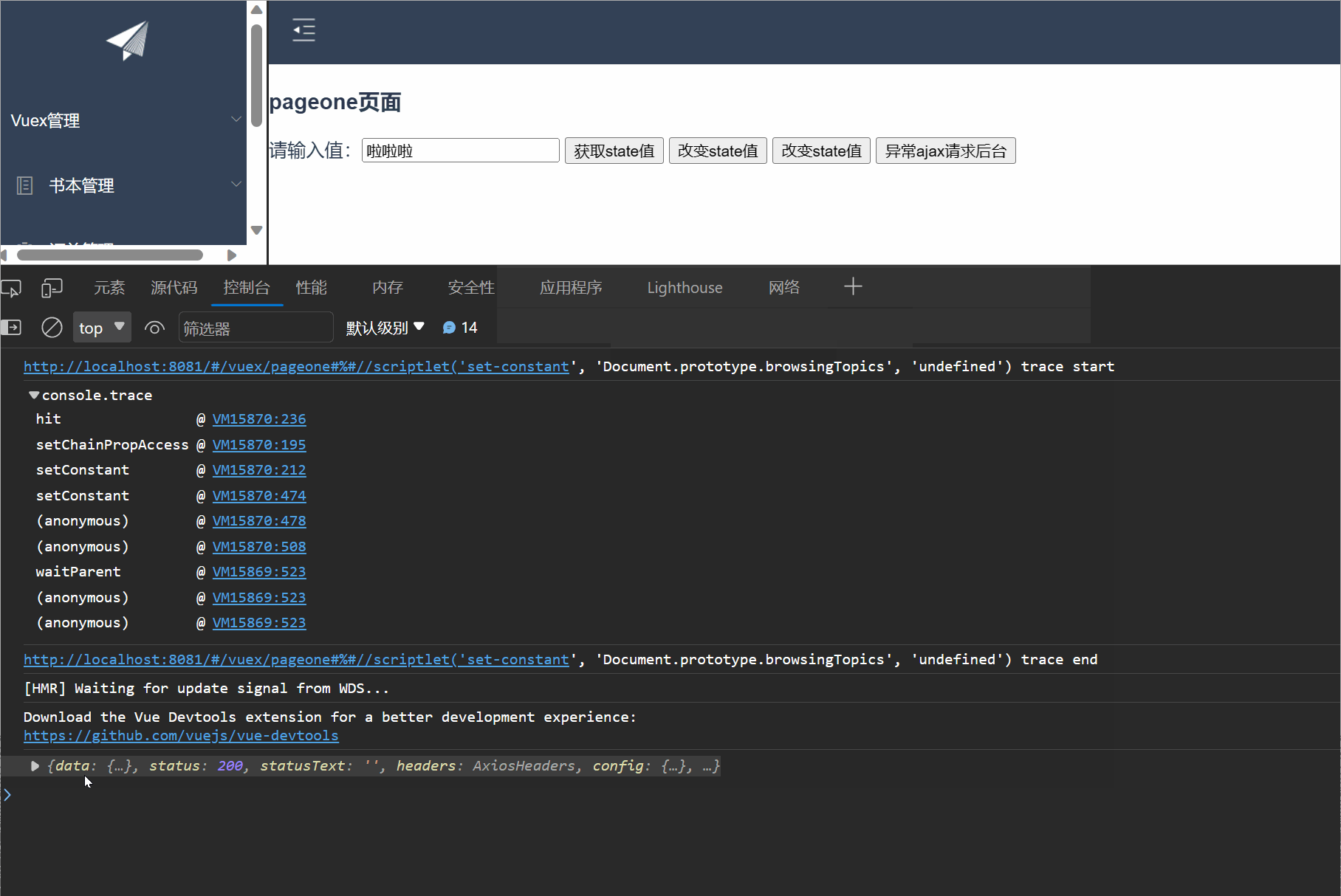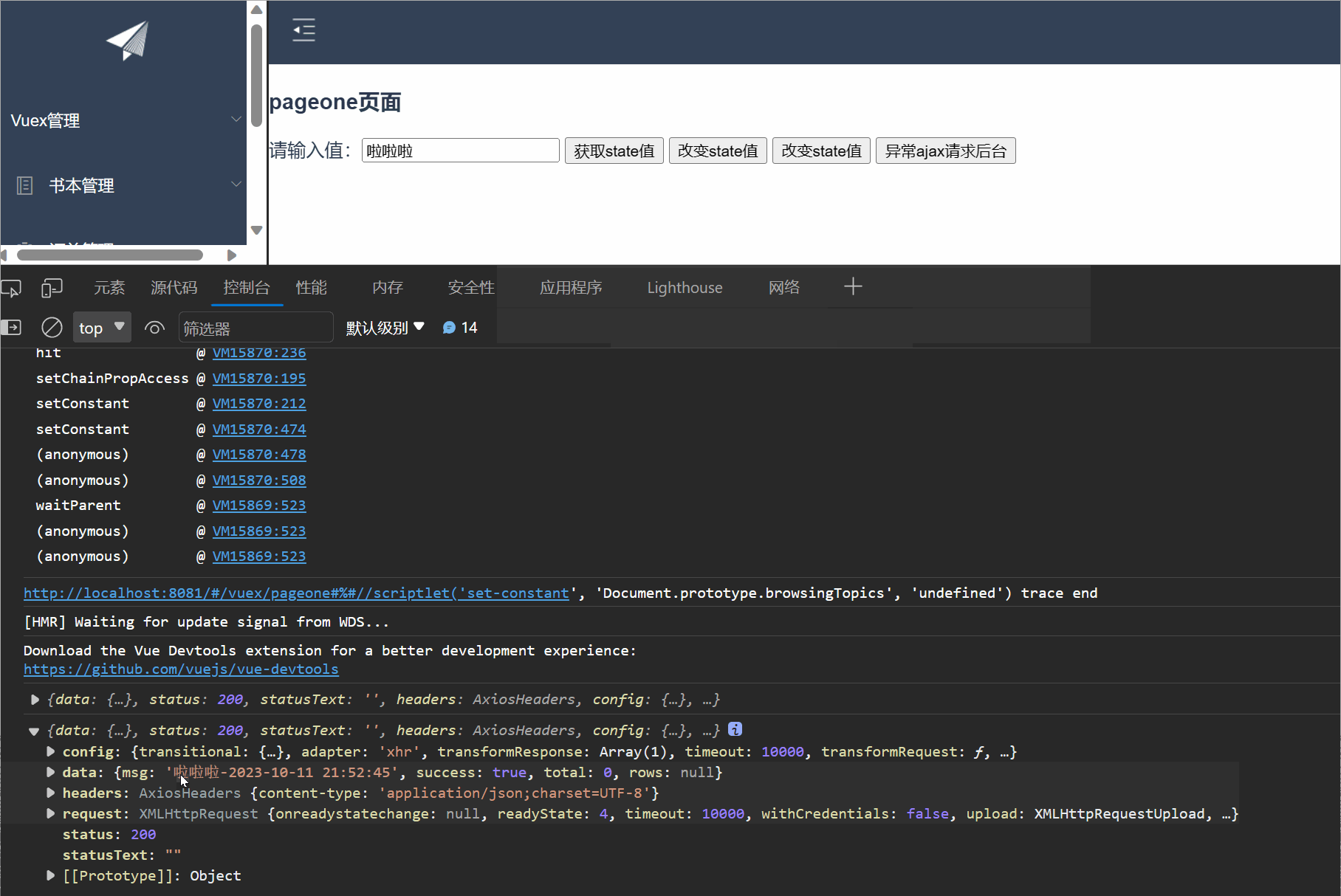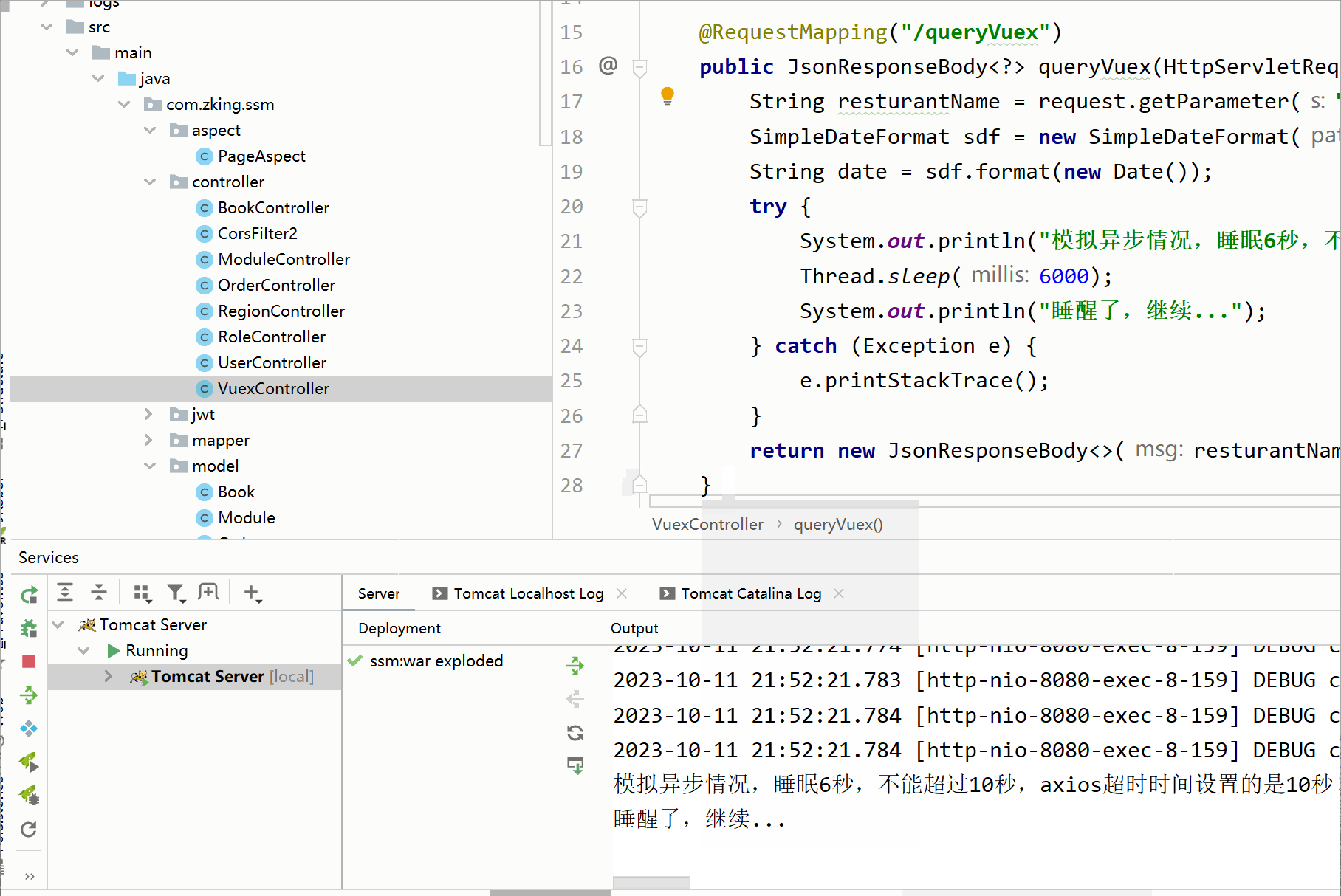
【Vue】之Vuex的入门使用,取值,修改值,同异步请求处理---保姆级别教学
一,Vuex入门 1.1 什么是Vuex Vuex是一个专门为Vue.js应用程序开发的状态管理库。它用于管理应用程序中的共享状态,它采用集中式存储管理应用的所有组件的状态,使得状态的管理变得简单和可预测 官方解释:Vuex 是一个专为 Vue.js 应…...
ubuntu20.04 nerf Instant-ngp (下) 复现,自建数据集,导出mesh
参考链接 Ubuntu20.04复现instant-ngp,自建数据集,导出mesh_XINYU W的博客-CSDN博客 GitHub - NVlabs/instant-ngp: Instant neural graphics primitives: lightning fast NeRF and more youtube上的一个博主自建数据集 https://www.youtube.com/watch…...
【常见错误】SVN提交项目时,出现了这样的提示:“XXX“ is scheduled for addition, but is missing。
SVN提交项目时,出现了这样的提示:“XXX“ is scheduled for addition, but is missing。 原因是:之前用SVN提交过的文件/文件夹,被标记为"addition"状态,等待被加入到仓库。虽然你把这个文件删除了…...
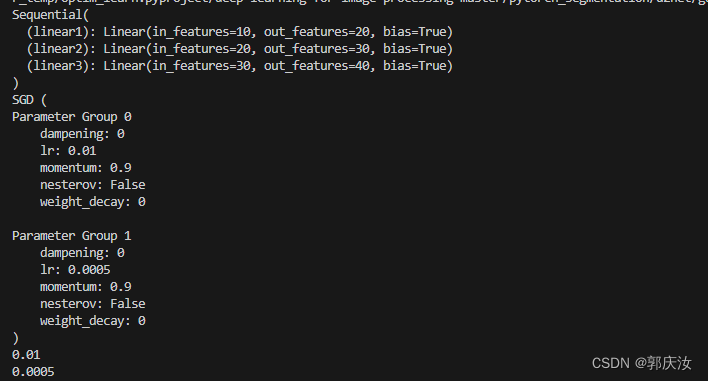
深度学习基础知识 给模型的不同层 设置不同学习率
深度学习基础知识 给模型的不同层 设置不同学习率 1、使用预训练模型时,可能需要将2、学习率设置方式: 1、使用预训练模型时,可能需要将 (1)预训练好的 backbone 的 参数学习率设置为较小值, (2…...

【Python 零基础入门】 Numpy
【Python 零基础入门】第六课 Numpy 概述什么是 Numpy?Numpy 与 Python 数组的区别并发 vs 并行单线程 vs 多线程GILNumpy 在数据科学中的重要性 Numpy 安装Anaconda导包 ndarraynp.array 创建数组属性np.zeros 创建np.ones 创建 数组的切片和索引基本索引切片操作数组运算 常…...

1600*C. Circle of Monsters(贪心)
Problem - 1334C - Codeforces 解析: 对于某个怪兽,他的耗费为两种情况,要么直接用子弹打,要么被前面的怪兽炸,显然第二种情况耗费更少。 统计出所有怪兽的 max(0,a[ i ] - b[ i - 1 ]ÿ…...

国外互联网巨头常用的项目管理工具揭秘
大型互联网公司有涉及多个团队和利益相关者的复杂项目。为了保持项目的组织性和效率,他们中的许多人依赖于项目管理工具。这些工具有助于跟踪任务,与团队成员沟通,并监控进度。让我们来看看一些大型互联网公司正在使用的项目管理工具。 1、Zo…...
, 盲注)
sql 注入(4), 盲注
sql 注入, 盲注 盲注适合在页面没有任何回显时使用. 测试页面有变化, 但是没有显示任何异常错误等信息. 情景: url: http://192.168.112.200/security/read.php?id1 服务器数据库名: learn一, boolean盲注 # 盲注可能需要一个一个字符去试探, 字符串处理函数经常会用到. 比…...

【string题解 C++】字符串相乘 | 翻转字符串III:翻转单词
字符串相乘 题面 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。 注意:不能使用任何内置的 BigIn…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
