算法:动态规划的入门理解
文章目录
- 算法原理
- 题目解析
- 第n个泰波那契数列
- 三步问题
- 使用最小花费爬楼梯
从本篇开始总结的是动态规划的一些内容,动态规划是算法中非常重要的一个版块,因此也是学习算法中的一个重点,在学习动态规划前应当要把动态规划的基础知识学习一下
算法原理
动态规划既然是一个新的算法,这个名字也是新名字,那么就要首先明确这个算法的名字代表什么含义
动态规划是什么?
动态规划其实就是dp表中的值所表示的含义
那什么又是dp表?
dp表是解决这类问题中必须要使用的一个内容,通常是借助vector来表示
dp表怎么写出来?
一般来说题目要求中会有一些提示,同时在分析问题的过程中,如果遇到了分析的过程中有重复的子问题,也可以借助这个逻辑写出一个状态转移方程,利用这个状态转移方程就可以填写到dp表中
状态转移方程
状态转移方程就是在动态规划中根据一部分提示找到dp表的填入方法,再根据这个方法就可以借助dp表解决问题,因此状态转移方程是解决问题的关键
题目解析
首先用一个比较简单的题目来上手动态规划
第n个泰波那契数列

对于这个题来说,可以用上面的动态规划的方法来处理:
首先创建一个dp表,再从题目中找到状态转移方程,再利用状态转移方程写入dp表,再利用dp表求出要找的数据
class Solution
{
public:int tribonacci(int n) {// 处理边界if(n==0){return 0;}if(n==1 || n==2){return 1;}// 创建dp表vector<int> dp(n+1);// 初始化dp表dp[0]=0;dp[1]=1;dp[2]=1;//填入dp表for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2]+dp[i-3];}// 返回值return dp[n];}
};
三步问题

分析问题:
假设现在有1个台阶,那么小孩跳到这个台阶的方法有1种,直接从地面走到第一个台阶上
假设现在有2个台阶,那么小孩跳到这个台阶的方法有2种,第一种从地面直接走到第二个台阶上,第二种是小孩从地面走到第一个台阶,再从第一个台阶走到第二个台阶上
假设现在有3个台阶,那么小孩跳到这个台阶的方法有4种,第一种直接跳到第三个台阶上,第二种先跳到第一个台阶,再从第一个台阶向第三个台阶跳,而从第一个台阶向第三个台阶跳又有两种,参考有2个台阶的方案,那么总共第二种方法有2种,第三种小孩跳到第二个台阶,再从第二个台阶跳到第三个台阶,因此总共有四种方法
假设现在有4个台阶,那么小孩跳到第四个台阶的方法总共有7种,先让小孩走到第一个台阶,再从第一个台阶走到第四个台阶即可,而小孩走到第一个台阶的方法有1种;也可以先让小孩走到第二个台阶,再从第二个台阶走到第四个台阶,而小孩走到第二个台阶的方法有2种;先让小孩走到第三个台阶,再从第三个台阶直接到第四个台阶,而直接让小孩走到第四个台阶的方法有4种,因此上面的这些总计是7种
假设现在有5个台阶,那么小孩跳到第五个台阶的方法有13种,先让小孩跳到第二个台阶,再从第二个台阶直接到第五个台阶…
因此规律就找到了,其实就是一个斐波那契数列的变形问题,利用上面的例题的思路就可以解决这个问题
class Solution
{
public:int waysToStep(int n) {vector<long long> dp(n+4);dp[0]=0;dp[1]=1;dp[2]=2;dp[3]=4;for(int i=4;i<=n;i++){dp[i]=dp[i-1]+dp[i-2]+dp[i-3];dp[i] %= 1000000007;}return dp[n];}
};
使用最小花费爬楼梯

此题也是动态规划中的一个典型题,这里从两个角度来看这道题
从最开始的介绍中可以知道,对于动态规划的问题来说,关键是dp[i]的意义和状态转移方程,在解决问题的过程中要优先对这两个部分进行思考和解决,那么两个不同的dp[i]的角度来看这个题
首先从第一个角度来看:
如果这里的dp[i]表示的是,上到第i个台阶需要花费多少钱:
那么可以这样思考问题,要知道上到第i个台阶需要多少钱,就必然要知道上到第i-1个台阶要花多少钱,再用这个钱加上上第i-1个台阶要花多少钱,由于一次可以上两个台阶,因此也要知道上到第i-2个台阶需要多少钱和上这个台阶需要多少钱,再比较一下从第i-1个台阶上划算还是从第i-2个台阶上划算,比较后就可以得到dp[i]的值,因此状态转移方程就很容易得到了
dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
此时注意一下边界初始化问题:在第0和第1个台阶是不需要花钱的,于是初始化为0即可,代码也可以很好的实现出来
class Solution
{
public:int minCostClimbingStairs(vector<int>& cost) {vector<int> dp(cost.size()+1);dp[0]=0;dp[1]=0;for(int i=2;i<=cost.size();i++){dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[cost.size()];}
};
以上为第一种思考的方式,dp[i]对应的意义还有其他,这里还可以理解为从第i个位置上到最顶上需要的花费,因此这里也可以借助这个意义来解决
那如果要求从第i个台阶上到顶端要花多少钱,需要知道从第i个台阶一次上一个台阶还是一次上两个台阶比较划算,因此这里又需要知道i+1和i+2的值,根据这两个的值决定一次上一个台阶还是上两个台阶,因此状态转移方程也可以得出来了:
dp[i]=min(dp[i+1]+cost[i],dp[i+2]+cost[i]);
那么代码的实现也可以得出:
class Solution
{
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int> dp(n);dp[n-1]=cost[n-1];dp[n-2]=cost[n-2];for(int i=n-3;i>=0;i--){dp[i]=min(dp[i+1]+cost[i],dp[i+2]+cost[i]);}return min(dp[0],dp[1]);}
};
相关文章:

算法:动态规划的入门理解
文章目录 算法原理题目解析第n个泰波那契数列三步问题使用最小花费爬楼梯 从本篇开始总结的是动态规划的一些内容,动态规划是算法中非常重要的一个版块,因此也是学习算法中的一个重点,在学习动态规划前应当要把动态规划的基础知识学习一下 算…...

最新版nacos 2.2.3服务注册与发现版本依赖问题
最新版nacos的注册服务时配置文件写的是对的,但就是在nacos web页面无法看见服务,此时你需要注意你的依赖是否正确 spring: application:name: orderservicecloud:nacos:discovery:server-addr: 122.51.115.127:8848父工程依赖:现在最新的s…...
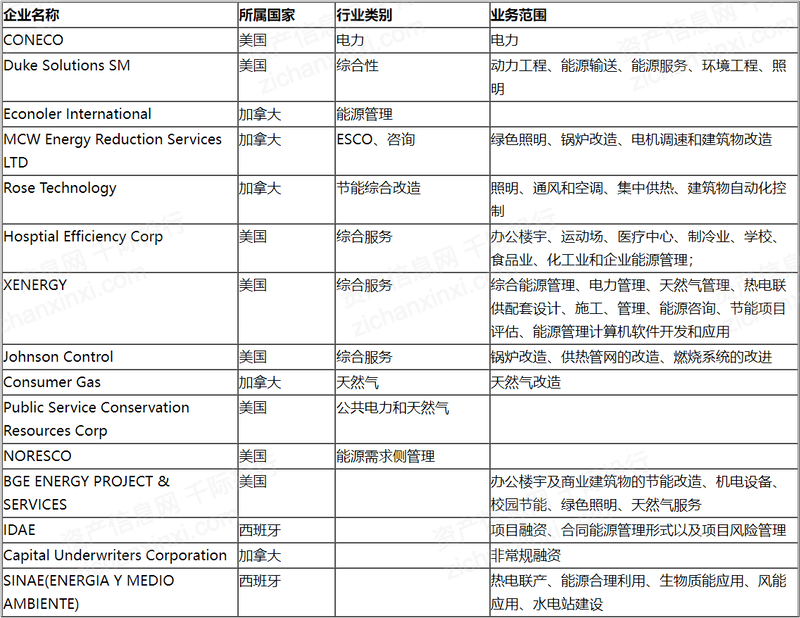
2023年中国合同能源管理行业研究报告
第一章 行业概况 1.1 定义及分类 合同能源管理 (Energy Performance Contracting, EPC) 是当前能源行业中一个重要的概念,它构建了一个桥梁,将节能服务公司 (Energy Management Company, EMCo) 与用能单位紧密联系在一起。通过特定的契约形式ÿ…...

php以半小时为单位,输出指定的时间范围
//可预订小时范围$hour [];for ($i$startHour*3600;$i<$endHour*3600;$i1800){//以半小时为单位输出$startHourItem date(H:i,strtotime(date(Y-m-d))$i);//小时开始$endHourItem date(H:i,strtotime(date(Y-m-d))$i1800);//当前时间再加半小时$hourItemStr $startHourI…...

Electron应用的 asar 打包 解压
前言: .asar文件是一种归档文件格式,通常用于封装Electron应用程序的资源。Electron是一个使得开发者能够使用Web技术构建跨平台桌面应用程序的框架。为了提高性能和简化部署,Electron应用程序的资源通常会被打包到一个.asar文件中。 安装 as…...

蓝桥等考Python组别十七级003
第一部分:选择题 1、Python L17 (15分) 运行下面程序,输出的结果是( )。 def func(x, y): return (x + y) // 3 print(func(7, 5)) 2468正确答案:B 2、Python L17 (15</...

Redis概述和与SpringBoot的整合
Redis是一种高性能的键值对存储数据库,它支持多种数据结构,包括字符串、哈希、列表、集合和有序集合等。Redis具有快速、可靠、灵活和可扩展等特点,也被广泛应用于缓存、队列和排行榜等场景。 SpringBoot是一种基于Spring框架的快速开发脚手…...
 函数:实现精确的数值舍入操作)
Python 中的 round() 函数:实现精确的数值舍入操作
round(x, n) 函数用于对数值 x 进行舍入操作,并指定保留的小数位数为 n。它的工作原理如下: 如果 x 的小数位数小于等于 n,则直接返回 x 本身。例如,round(3.1415, 2) 将返回 3.14。 如果 x 的小数位数大于 n,则按照四…...

在springboot中如何开启Bean数据校验
①:添加JSR303规范坐标与Hibernate校验框架对应坐标 <dependency><groupId>javax.validation</groupId><artifactId>validation-api</artifactId> </dependency><dependency><groupId>org.hibernate.validator<…...

【C语言好题系列三】
文章目录 学习导航一. 选择题二. 编程题(力扣/牛客网)三. 总结 学习导航 一. 选择题 如下程序的运行结果是(D) char c[5]{a, b, \0, c, \0}; printf("%s", c);A: ‘a’ ‘b’ B: ab\0c\0 C: ab c D: ab 答案解析: 正…...

ElasticSearch搜索引擎:常用的存储mapping配置项 与 doc_values详细介绍
一、ES的数据存储结构: ES底层使用 Lucene 存储数据,Lucene 的索引包含以下部分: A Lucene index is made of several components: an inverted index, a bkd tree, a column store (doc values), a document store (stored fields) and te…...

[Spring]事务的传播机制
一、背景 Mysql在修改完数据后,默认会自动触发事务Commit提交。 而在我们服务的一个方法里,需要多次修改Mysql记录。 为了保证原子性,我们需要将Mysql设为手动提交,多次修改后再commit提交。 二、Spring事务 1、编程式事务管理…...

linux下,如何查看一个文件的哈希值md5以及sha264
在linux终端中,可能存在多个相似的文件,而哈希值可以唯一确定一个文件。文件的哈希值计算可以有以下两种方式,MD5和SHA256,现将两种方式罗列如下: 1、MD5 命令:$ md5sum FileName 一个文件的 MD5 是固定的…...
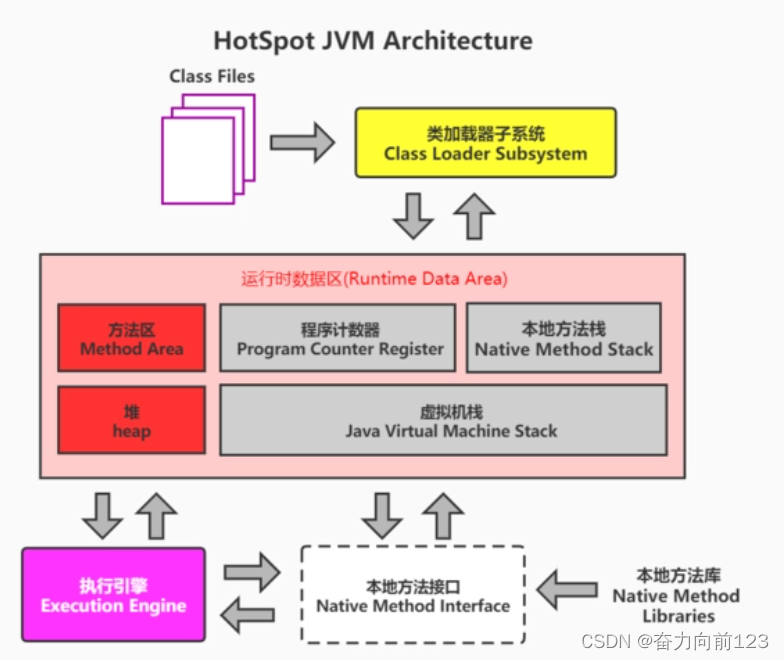
Java类加载过程
一、前言 我们都知道计算机的底层逻辑都是0和1的编码,当然除了现在所研究的量子计算除外。那么我们在计算机所做的一切操作,底层原理是不是都可以翻译到0和1呢。如果刨根问底的话,可以这么说,当然0和1的表示也属于逻辑门电路电的…...
人脸活体检测技术的应用,有效避免人脸识别容易被攻击的缺陷
随着软件算法和物理终端的进步,人脸识别现在越来越被广泛运用到生活的方方面面,已经成为了重要的身份验证手段,但同时也存在着自身的缺陷,目前常规人脸识别技术可以精准识别目标人像特征,并迅速返回比对结果࿰…...

大数据发展史
一、hadoop发展史 hadoop创始人Doug Cutting,主要为了实现Google类似全文搜索功能,该功能是基于Lucene框架进行优化升级,索引引擎; 2001年底Lucence成为Apache基金会的一个子项目,当时为了解决存储海量数据困难,检索海量速度慢,可以说Google是hadoop的思想之源; GFS…...

有关范数的学习笔记
向量的【范数】:模长的推广,柯西不等式_哔哩哔哩_bilibili 模长 范数 这里UP主给了说明 点赞 范数理解(0范数,1范数,2范数)_一阶范数-CSDN博客 出租车/曼哈顿范数 det()行列式 正定矩阵(Posit…...

如何通过MES系统提高生产计划效率?
导 读 ( 文/ 1730 ) 在现代制造业中,通过制造执行系统(MES)系统来提高生产计划效率是至关重要的。本文将介绍如何通过MES系统来优化生产计划,包括实时数据分析、智能排程和协同协作。通过这些关键方法,企业可以提高生产…...

持续提升信息安全运维保障服务能力,天玑科技助力企业快速实现数字化转型
近年来,以互联网、云计算、大数据、物联网为代表的新一代信息技术快速发展。给人们的生产生活方式带来方便的同时,也给信息系统的安全带来了严峻的挑战。我国信息化和信息安全保障工作的不断深入推进,以应急处理、风险评估、灾难恢复、系统测…...
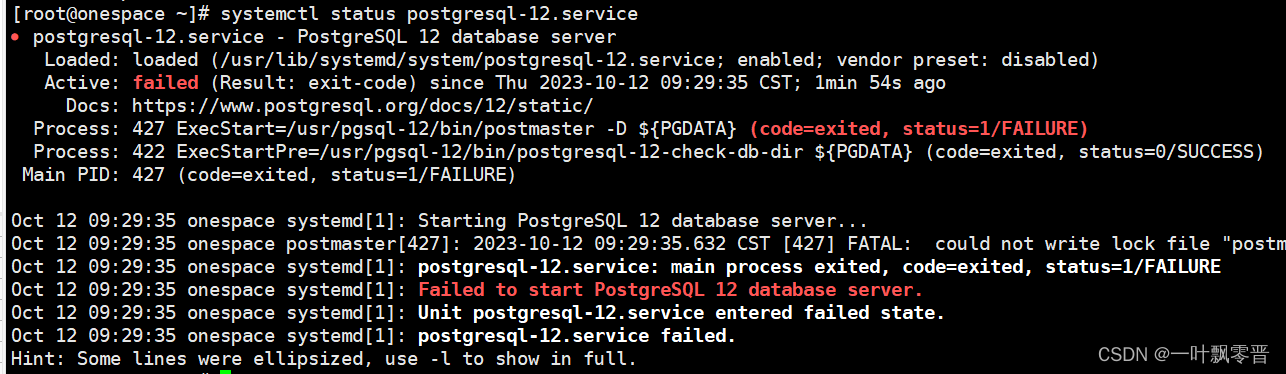
【PostgreSQL启动,停止命令(重启)】
找到 /usr/lib/systemd/system文件夹路径看是否包含 postgresql服务 关闭服务: systemctl stop postgresql-12.service启动服务 systemctl start postgresql-12.service重启服务 systemctl restart postgresql-12查看状态 systemctl status postgresql-12.servi…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
