有关范数的学习笔记
向量的【范数】：模长的推广，柯西不等式_哔哩哔哩_bilibili
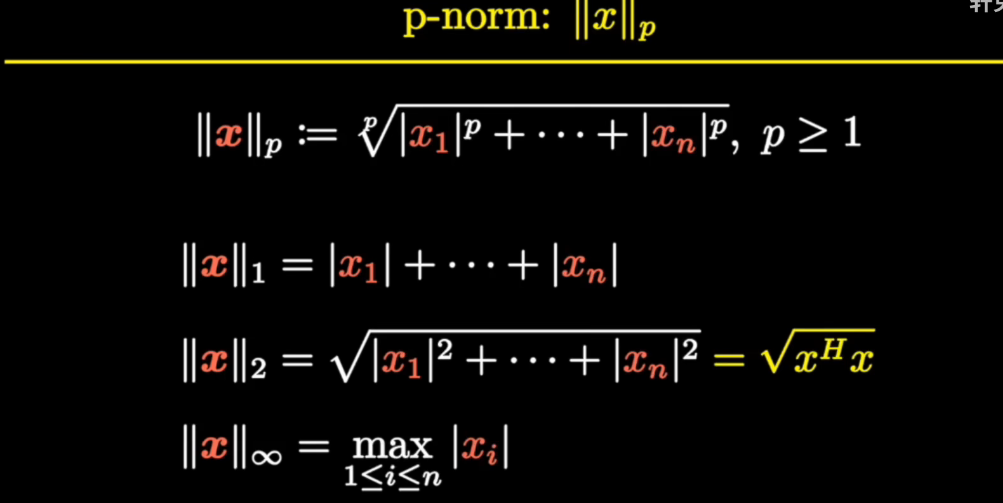
范数理解（0范数，1范数，2范数）_一阶范数-CSDN博客
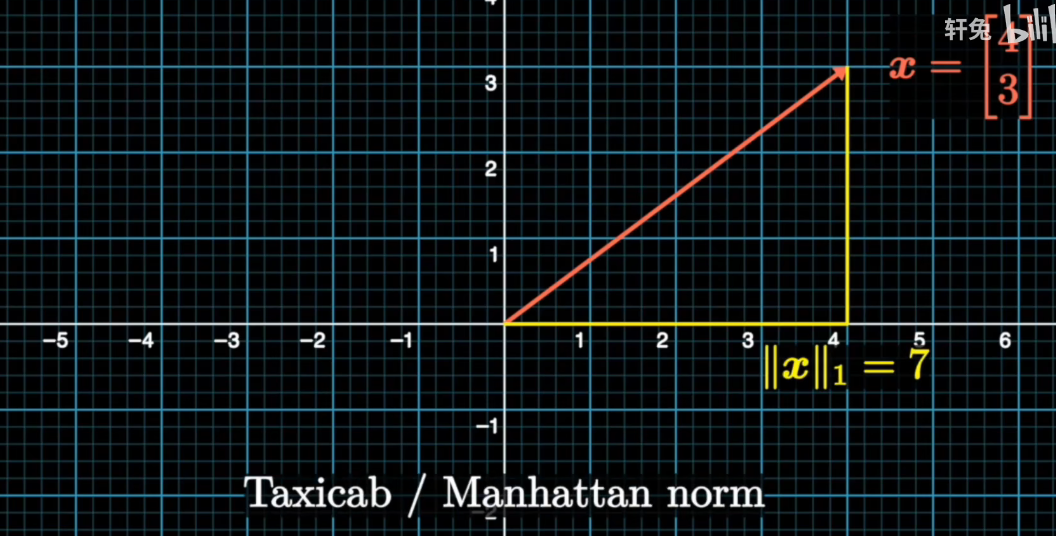
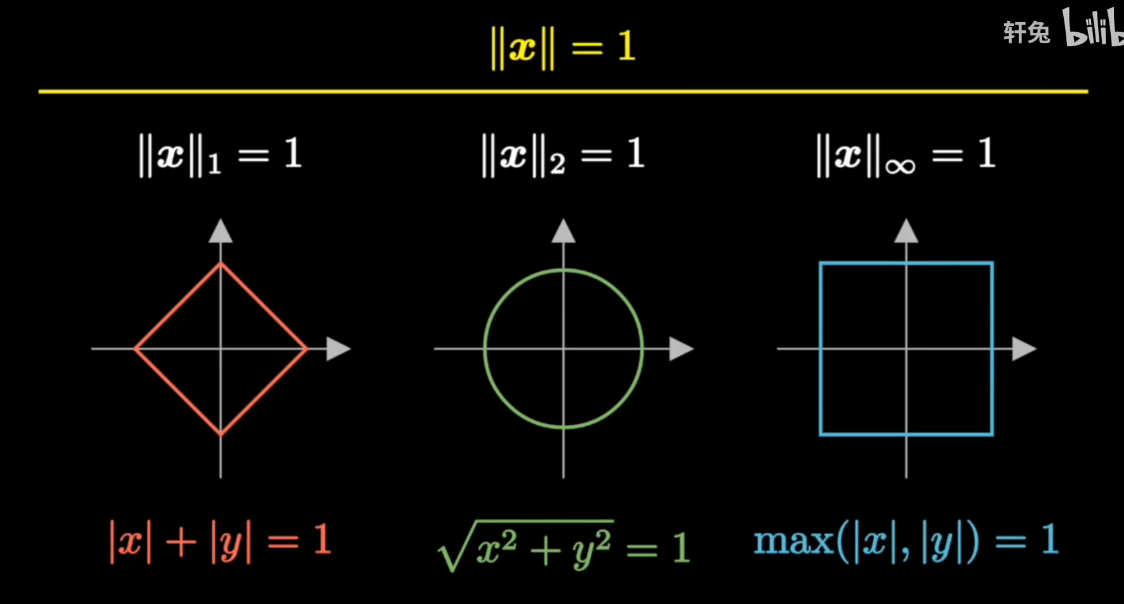
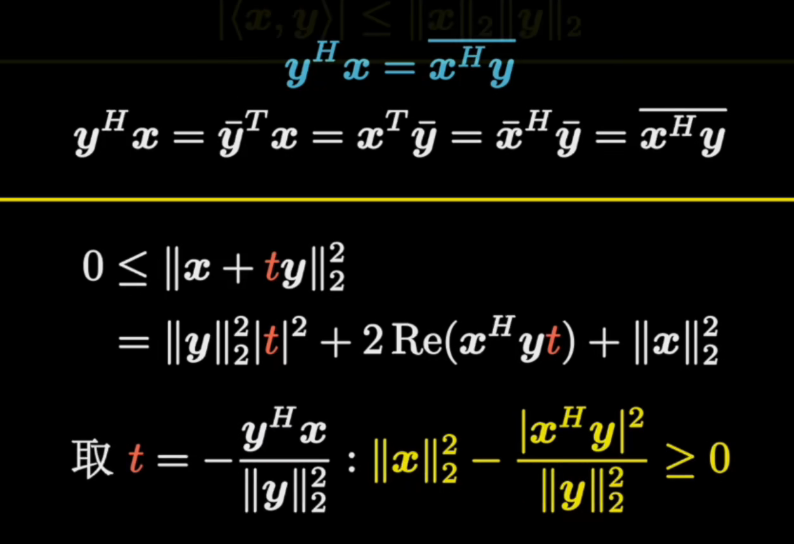
正定矩阵（Positive Definite Matrix）是指一个对称矩阵A，对于任意非零向量x，都满足x^T * A * x > 0，其中^T表示向量的转置。换句话说，正定矩阵的所有特征值都大于零。
半正定矩阵（Positive Semidefinite Matrix）是指一个对称矩阵A，对于任意非零向量x，都满足x^T * A * x ≥ 0。换句话说，半正定矩阵的所有特征值都大于等于零。
这里的正不正定及是否半正定可由特征值判断，之前都学了啥？？？？
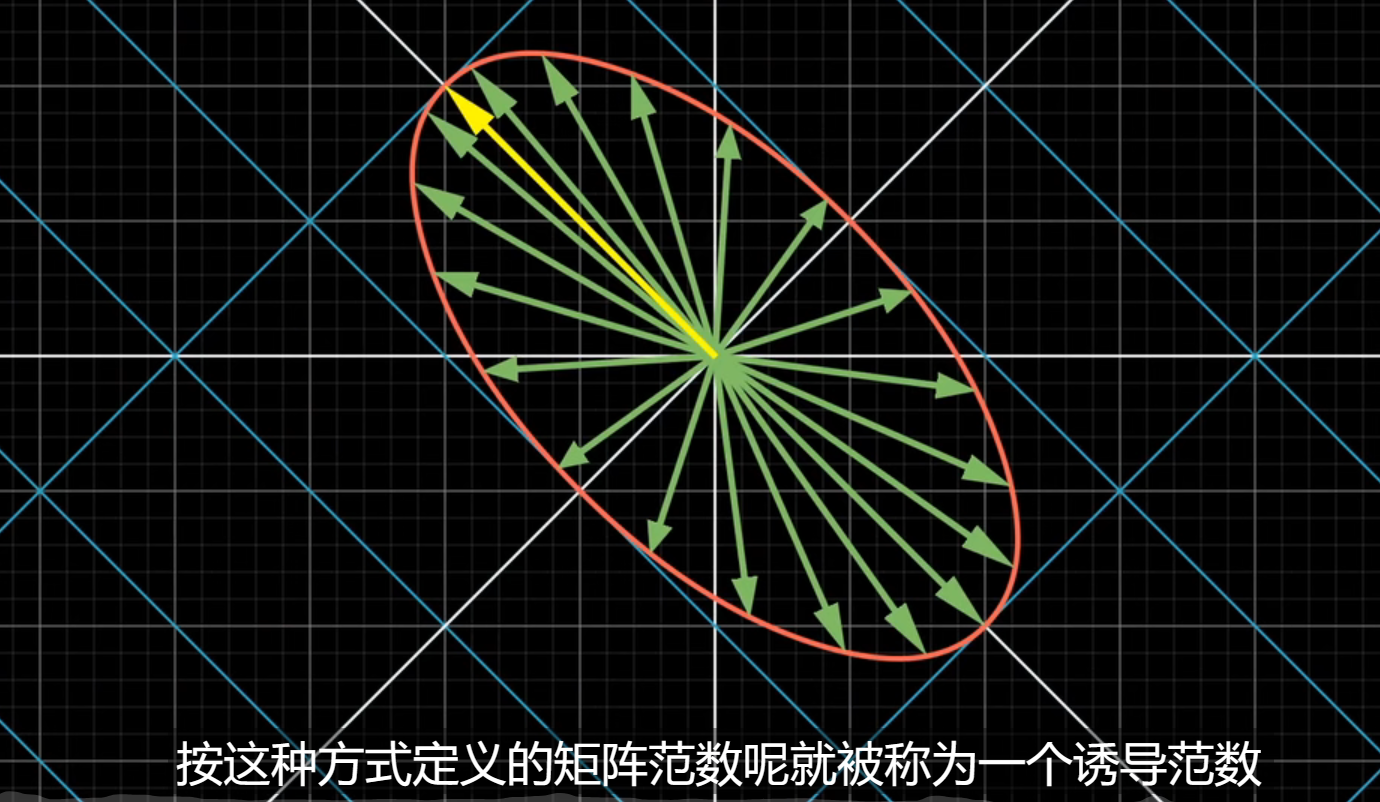
矩阵的【范数】：也是一种长度
矩阵刻画的是一种线性变换，如何衡量变换的长度，有一种想法是在某种范数的情况下考虑某种单位向量，然后在变换后取变换最长的长度作为向量的长度：
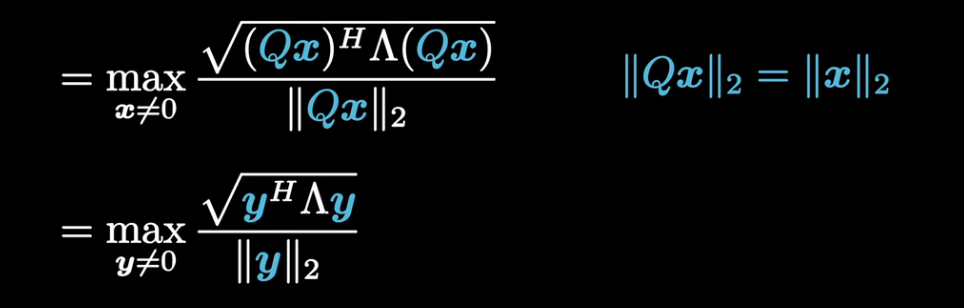
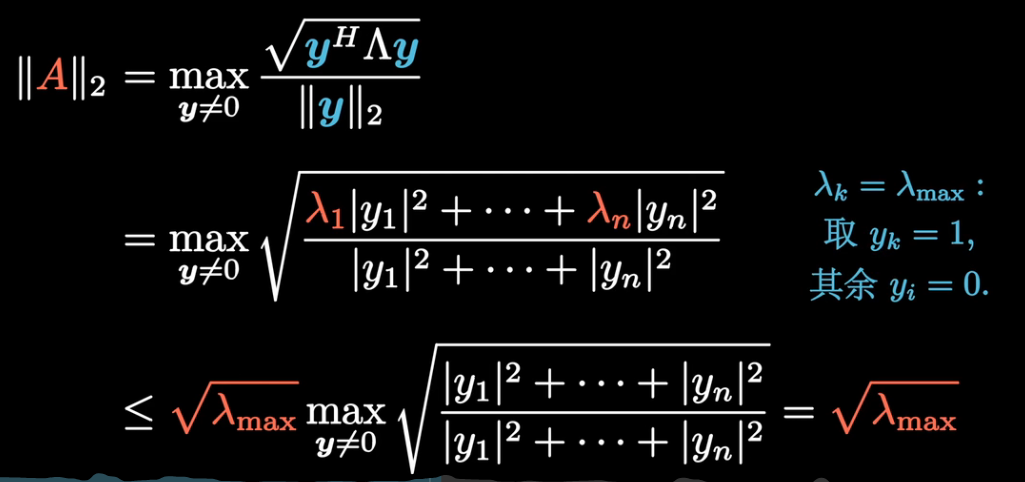
矩阵的一范数，等于其最大的列和
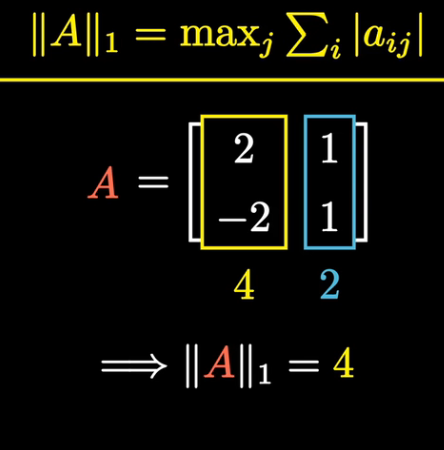
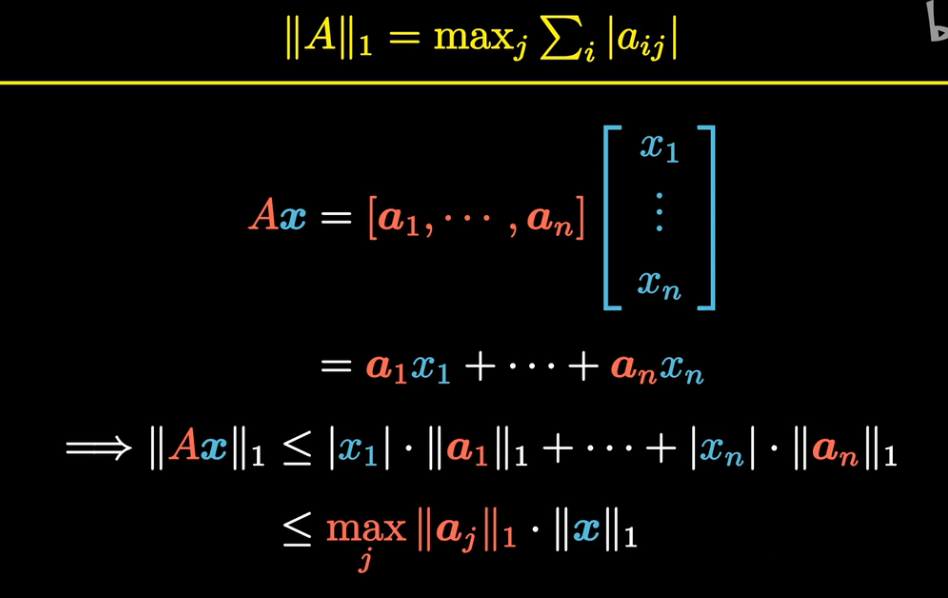
矩阵的无穷范数 是矩阵的最大行和
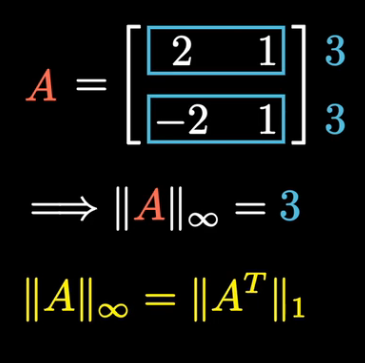
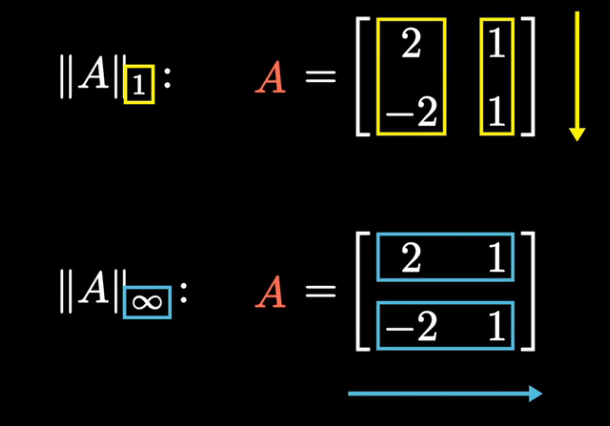
Frobenius norm
我这脑袋瓜子记不住啊，用到的时候再看看。。。
相关文章：
有关范数的学习笔记
向量的【范数】：模长的推广，柯西不等式_哔哩哔哩_bilibili 模长 范数 这里UP主给了说明 点赞 范数理解（0范数，1范数，2范数）_一阶范数-CSDN博客 出租车/曼哈顿范数 det()行列式 正定矩阵（Posit…...
如何通过MES系统提高生产计划效率？
导 读 ( 文/ 1730 ) 在现代制造业中，通过制造执行系统（MES）系统来提高生产计划效率是至关重要的。本文将介绍如何通过MES系统来优化生产计划，包括实时数据分析、智能排程和协同协作。通过这些关键方法，企业可以提高生产…...
持续提升信息安全运维保障服务能力，天玑科技助力企业快速实现数字化转型
近年来，以互联网、云计算、大数据、物联网为代表的新一代信息技术快速发展。给人们的生产生活方式带来方便的同时，也给信息系统的安全带来了严峻的挑战。我国信息化和信息安全保障工作的不断深入推进，以应急处理、风险评估、灾难恢复、系统测…...
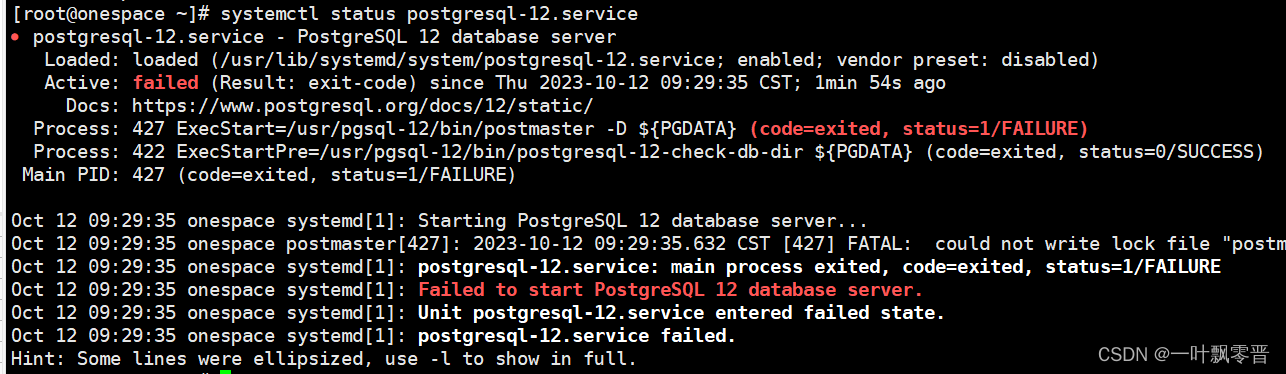
【PostgreSQL启动，停止命令(重启)】
找到 /usr/lib/systemd/system文件夹路径看是否包含 postgresql服务 关闭服务： systemctl stop postgresql-12.service启动服务 systemctl start postgresql-12.service重启服务 systemctl restart postgresql-12查看状态 systemctl status postgresql-12.servi…...
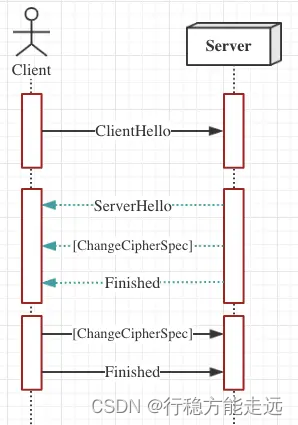
TLS 详解
目录 TLS 定义HTTPS HTTP over TLS.加密记录层分片 (Fragmentation)记录压缩和解压缩 (Record compression and decompression)空或标准流加密 (Null or standard stream cipher)CBC 块加密 (分组加密)记录有效载荷保护 (Record payload protection)密钥计算 (Key calculation…...
【重拾C语言】十、递归程序设计
目录 前言 十、递归程序设计 10.1 计算n！——递归程序设计 10.2 程序设计实例 10.2.1 汉诺塔 10.2.2 齿轮 10.2.3 组合 10.3 计算算术表达式的值——间接递归 10.4 递归程序执行过程 前言 递归程序设计是一种编程技术，其中一个函数通过调用自身…...
SQL日期字段去时分秒
substring( convert(varchar,[申请日期],120),1,10) AS 申请日期 运行结果对比展示 申请日期申请日期2022-12-24 00:00:00.0002022-12-24 说明： substring(...): 这是SQL中用于提取字符串一部分的函数。 convert(varchar, 申请日期, 120): 这部分将日期值&#…...
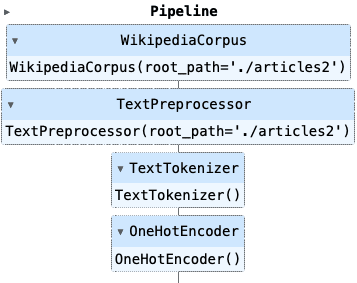
NLP项目：维基百科文章爬虫和分类【02】 - 语料库转换管道
一、说明 我的NLP项目在维基百科条目上下载、处理和应用机器学习算法。相关上一篇文章中，展示了项目大纲，并建立了它的基础。首先，一个 Wikipedia 爬网程序对象，它按名称搜索文章，提取标题、类别、内容和相关页面&…...
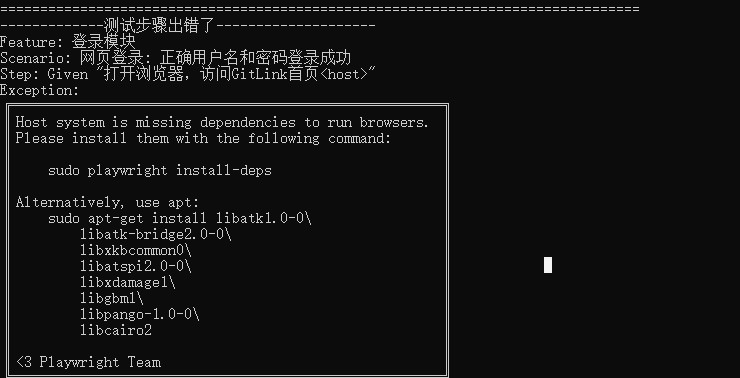
如何在Ubuntu 20.04.6 LTS系统上运行Playwright自动化测试
写在前面 这里以 Ubuntu 20.04.6 LTS为例。示例代码：自动化测试代码。 如果过程中遇到其他非文本中提到的错误，可以使用搜索引擎搜索错误，找出解决方案，再逐步往下进行。 一、 环境准备 1.1 安装python3 1.1.1 使用APT安装Py…...
c++ sort函数cmp比较参数传入
开始 假定有一个结构体 struct node{int p,r,val; };第一种 定义cmp函数，sort直接传入cmp bool cmp(node a,node b){return a.p<b.p;} sort(vec.begin(),vec.end(),cmp);第二种 lamada表达式？？这个中括号里面可以不为空，但是…...
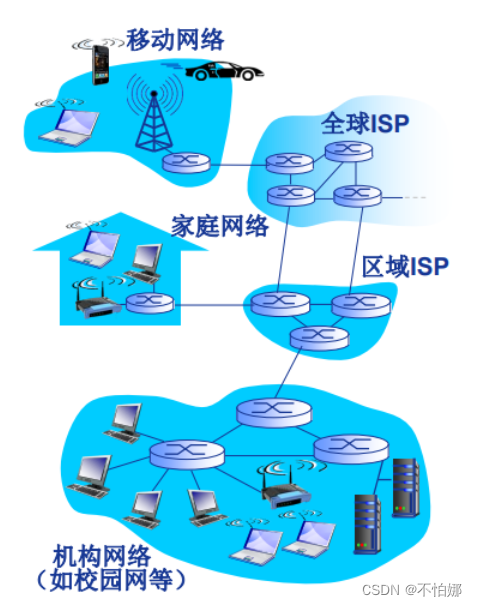
【计算机网络笔记】什么是计算机网络？
前言计算机网络的定义交换网络什么是Internet从组成细节角度看从服务角度看 最后感谢 💖 本篇文章总字数：1342字 预计阅读时间：5~10min 建议收藏之后慢慢阅读 前言 计算机网络通信技术计算机技术。 计算机网络是通信技术与计算机技术紧密结…...
极简C++（2） 类与对象
类与对象的基本概念 CLASS类将数据以及数据上的操作封装在一起 OBJECT对象是有具体类类型的变量 打个比方，类就像一个制作月饼的摸具，那么我们可以通过这个摸具来放入面粉和馅料编程一个月饼，那么摸具就是类，而各种各样的月饼便是…...
【Java 进阶篇】JavaScript流程控制语句详解
JavaScript是一门高级编程语言，具备丰富的流程控制语句，用于控制程序的执行流程。在本篇博客中，我们将深入探讨JavaScript的流程控制语句，包括条件语句、循环语句、以及其他一些控制语句。这篇博客将逐步介绍这些概念，…...
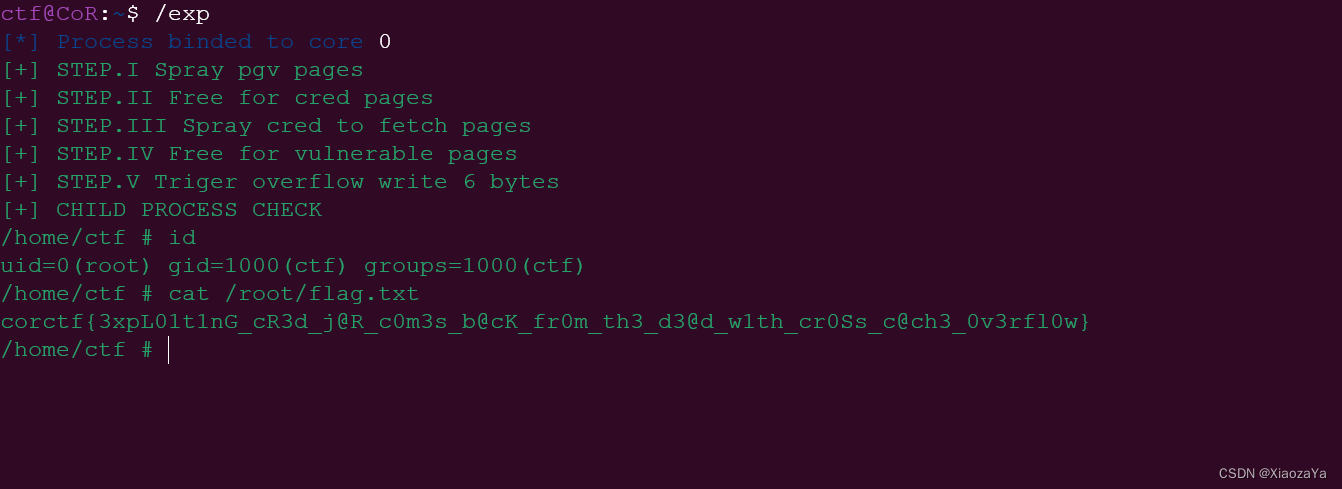
【Page-level Heap Fengshui -- Cross-Cache Overflow】corCTF2022-cache-of-castaways
前言 什么叫 Cross Cache 呢？其实就是字面意思，我们知道内核中的大部分结构体都有自己的专属 slab 内存池。那现在我们可以想象一下这个场景，我们拥有一个特定 kmem-cache 的溢出漏洞，那么我们该如何利用呢？ 程序分析…...
vue-mixin
1.vue中，混入(mixin)是一种特殊的使用方式。一个混入对象可以包含任意的组件配置选项(data, props, components, watch,computed…)可以根据需求"封装"一些可复用的单元，并在使用时根据一定的策略合并到组件的选项中，使用时和组件自…...
力扣刷题 day43：10-13
1.完全平方数 给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。 完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 …...
3、在docker 容器中安装tomcat
１、在服务器上查找tomcat镜像,查看前5条 docker search tomcat --limit 5 2、拉取镜像到本地 拉取官方的tomcat到本地 docker pull tomcat:9.0.34-jdk8 3、查看本地镜像 docker images |grep tomcat 4、启动tomcat 服务 使用默认配置 docker ru…...
工业互联网系列1 - 智能制造中有哪些数据在传输
工业互联网以网络为基础，需要传输的数据种类多种多样，这些数据对于实时监控、生产优化、设备维护和决策支持等方面都至关重要。 以下是一些常见智能制造业中需要传输的数据类型： 传感器数据：制造设备上安装的传感器（如…...
centos7部署Nginx和RabbitMQ
文章目录 Nginx安装部署【简单】简介安装 RabbitMQ安装部署【简单】简介安装 Nginx安装部署【简单】 简介 Nginx (engine x) 是一个高性能的HTTP和反向代理web服务器，同时也提供了IMAP/POP3/SMTP服务。Nginx可以托管用户编写的WEB应用程序成为可访问的网页服务&am…...
Nacos集群搭建
Nacos集群搭建 1.集群结构图 Nacos集群图： 其中包含3个nacos节点，然后一个负载均衡器代理3个Nacos。这里负载均衡器可以使用nginx。 三个nacos节点的地址： 节点ipportnacos1192.168.150.18845nacos2192.168.150.18846nacos3192.168.150…...
UE5 学习系列（二）用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇，在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下： 【Note】：如果你已经完成安装等操作，可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作，重…...
React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子，用于处理异步操作（如数据加载）中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误：捕获在 loader 或 action 中发生的异步错误替…...
Linux 文件类型，目录与路径，文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件：-（纯文本文件，二进制文件，数据格式文件） 如文本文件、图片、程序文件等。 目录文件：d（directory） 用来存放其他文件或子目录。 设备…...
TDengine 快速体验（Docker 镜像方式）
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能，本节首先介绍如何通过 Docker 快速体验 TDengine，然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker，请使用 安装包的方式快…...
VB.net复制Ntag213卡写入UID
本示例使用的发卡器：https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...
Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...
IGP（Interior Gateway Protocol，内部网关协议）
IGP（Interior Gateway Protocol，内部网关协议） 是一种用于在一个自治系统（AS）内部传递路由信息的路由协议，主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...
java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具，自己手写的难度，恐怕高级程序员花费一年的事件，也…...
visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中，选择 环境 -> 常规 ，将其中的颜色主题改成深色 点击确定，更改完成...
系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log，共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题，不能使用ELK只能使用…...