当前位置： 首页 > news >正文

SQL日期字段去时分秒

news 2025/7/8 0:33:42 
substring( convert(varchar,[申请日期],120),1,10) AS 申请日期

运行结果对比展示

申请日期申请日期
2022-12-24 00:00:00.0002022-12-24 

说明：

  1. substring(...): 这是SQL中用于提取字符串一部分的函数。

  2. convert(varchar, 申请日期, 120): 这部分将日期值（申请日期）转换为VARCHAR数据类型，使用代码中指定的格式 '120'。在SQL Server中，格式 '120' 代表ISO 8601日期格式（yyyy-mm-dd）。因此，它将日期转换为格式为 'yyyy-mm-dd' 的字符串。

  3. substring(..., 1, 10): 在进行转换后，它使用substring函数从结果字符串中提取前10个字符。在ISO 8601格式中，前10个字符表示日期（yyyy-mm-dd）。

相关文章：

SQL日期字段去时分秒

substring( convert(varchar,[申请日期],120),1,10) AS 申请日期 运行结果对比展示 申请日期申请日期2022-12-24 00:00:00.0002022-12-24 说明： substring(...): 这是SQL中用于提取字符串一部分的函数。 convert(varchar, 申请日期, 120): 这部分将日期值&#…...

编程日记 2023/10/14 6:25:28

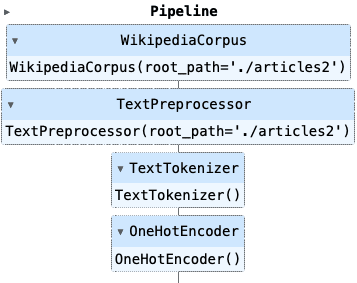
NLP项目：维基百科文章爬虫和分类【02】 - 语料库转换管道

一、说明 我的NLP项目在维基百科条目上下载、处理和应用机器学习算法。相关上一篇文章中，展示了项目大纲，并建立了它的基础。首先，一个 Wikipedia 爬网程序对象，它按名称搜索文章，提取标题、类别、内容和相关页面&…...

编程日记 2023/10/14 6:24:26

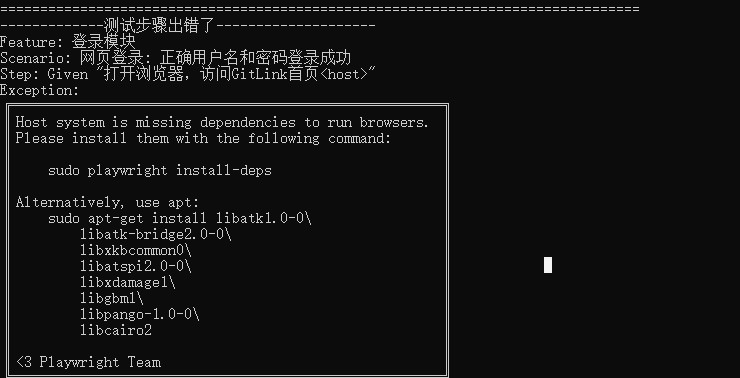
如何在Ubuntu 20.04.6 LTS系统上运行Playwright自动化测试

写在前面 这里以 Ubuntu 20.04.6 LTS为例。示例代码：自动化测试代码。 如果过程中遇到其他非文本中提到的错误，可以使用搜索引擎搜索错误，找出解决方案，再逐步往下进行。 一、 环境准备 1.1 安装python3 1.1.1 使用APT安装Py…...

编程日记 2023/10/14 6:22:23

c++ sort函数cmp比较参数传入

开始 假定有一个结构体 struct node{int p,r,val; };第一种 定义cmp函数&#xff0c;sort直接传入cmp bool cmp(node a,node b){return a.p<b.p;} sort(vec.begin(),vec.end(),cmp);第二种 lamada表达式&#xff1f;&#xff1f;这个中括号里面可以不为空&#xff0c;但是…...

编程日记 2023/10/14 6:20:20

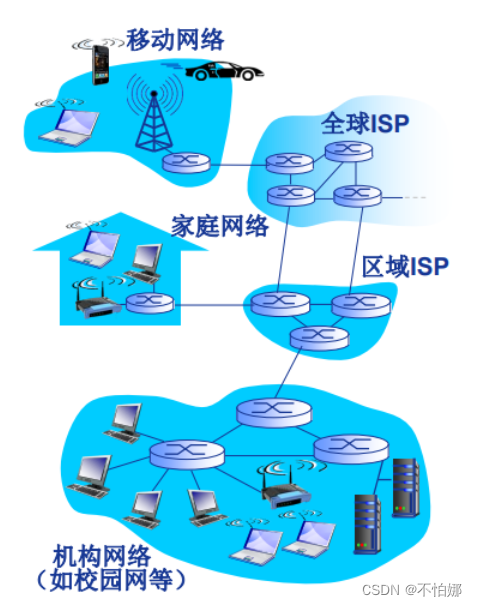
【计算机网络笔记】什么是计算机网络？

前言计算机网络的定义交换网络什么是Internet从组成细节角度看从服务角度看 最后感谢 &#x1f496; 本篇文章总字数&#xff1a;1342字 预计阅读时间&#xff1a;5~10min 建议收藏之后慢慢阅读 前言 计算机网络通信技术计算机技术。 计算机网络是通信技术与计算机技术紧密结…...

编程日记 2023/10/14 6:19:19

极简C++（2） 类与对象

类与对象的基本概念 CLASS类将数据以及数据上的操作封装在一起 OBJECT对象是有具体类类型的变量 打个比方&#xff0c;类就像一个制作月饼的摸具&#xff0c;那么我们可以通过这个摸具来放入面粉和馅料编程一个月饼&#xff0c;那么摸具就是类&#xff0c;而各种各样的月饼便是…...

编程日记 2023/10/14 6:18:17

【Java 进阶篇】JavaScript流程控制语句详解

JavaScript是一门高级编程语言&#xff0c;具备丰富的流程控制语句&#xff0c;用于控制程序的执行流程。在本篇博客中&#xff0c;我们将深入探讨JavaScript的流程控制语句&#xff0c;包括条件语句、循环语句、以及其他一些控制语句。这篇博客将逐步介绍这些概念&#xff0c;…...

编程日记 2023/10/14 6:17:15

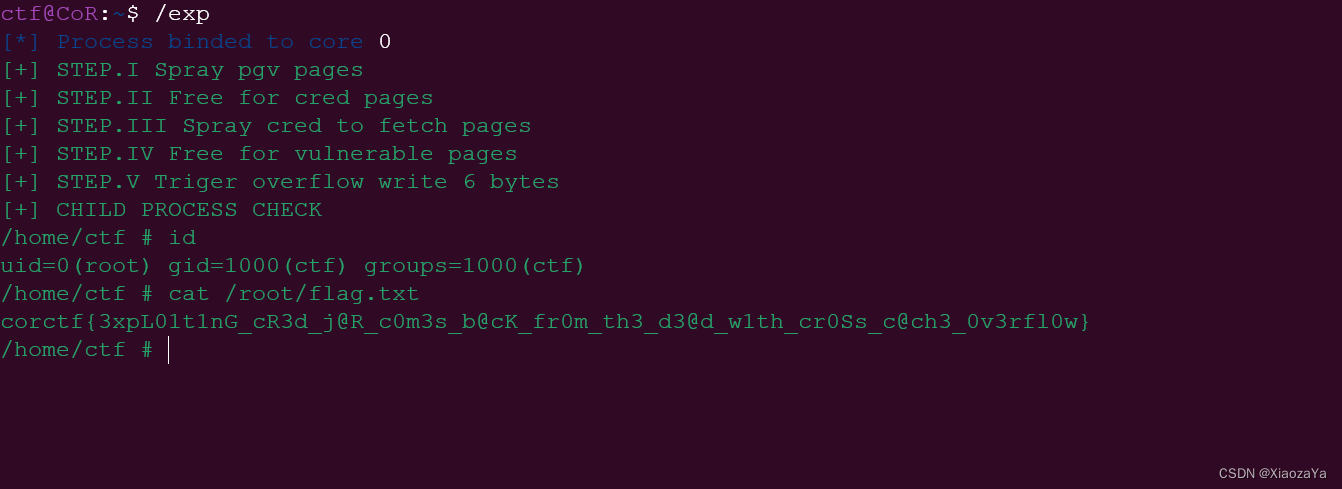
【Page-level Heap Fengshui -- Cross-Cache Overflow】corCTF2022-cache-of-castaways

前言 什么叫 Cross Cache 呢&#xff1f;其实就是字面意思&#xff0c;我们知道内核中的大部分结构体都有自己的专属 slab 内存池。那现在我们可以想象一下这个场景&#xff0c;我们拥有一个特定 kmem-cache 的溢出漏洞&#xff0c;那么我们该如何利用呢&#xff1f; 程序分析…...

编程日记 2023/10/14 6:16:14

vue-mixin

1.vue中&#xff0c;混入(mixin)是一种特殊的使用方式。一个混入对象可以包含任意的组件配置选项(data, props, components, watch,computed…)可以根据需求"封装"一些可复用的单元&#xff0c;并在使用时根据一定的策略合并到组件的选项中&#xff0c;使用时和组件自…...

编程日记 2023/10/14 6:14:11

力扣刷题 day43：10-13

1.完全平方数 给你一个整数 n &#xff0c;返回 和为 n 的完全平方数的最少数量 。 完全平方数 是一个整数&#xff0c;其值等于另一个整数的平方&#xff1b;换句话说&#xff0c;其值等于一个整数自乘的积。例如&#xff0c;1、4、9 和 16 都是完全平方数&#xff0c;而 3 …...

编程日记 2023/10/14 6:12:09

3、在docker 容器中安装tomcat

&#xff11;、在服务器上查找tomcat镜像,查看前5条 docker search tomcat --limit 5​​​​​​​ 2、拉取镜像到本地 拉取官方的tomcat到本地 docker pull tomcat:9.0.34-jdk8 3、查看本地镜像 docker images |grep tomcat 4、启动tomcat 服务 使用默认配置 docker ru…...

编程日记 2023/10/14 6:11:07

工业互联网系列1 - 智能制造中有哪些数据在传输

工业互联网以网络为基础&#xff0c;需要传输的数据种类多种多样&#xff0c;这些数据对于实时监控、生产优化、设备维护和决策支持等方面都至关重要。 以下是一些常见智能制造业中需要传输的数据类型&#xff1a; 传感器数据&#xff1a;制造设备上安装的传感器&#xff08;如…...

编程日记 2023/10/14 6:10:06

centos7部署Nginx和RabbitMQ

文章目录 Nginx安装部署【简单】简介安装 RabbitMQ安装部署【简单】简介安装 Nginx安装部署【简单】 简介 Nginx (engine x) 是一个高性能的HTTP和反向代理web服务器&#xff0c;同时也提供了IMAP/POP3/SMTP服务。Nginx可以托管用户编写的WEB应用程序成为可访问的网页服务&am…...

编程日记 2023/10/14 6:07:03

Nacos集群搭建

Nacos集群搭建 1.集群结构图 Nacos集群图&#xff1a; 其中包含3个nacos节点&#xff0c;然后一个负载均衡器代理3个Nacos。这里负载均衡器可以使用nginx。 三个nacos节点的地址&#xff1a; 节点ipportnacos1192.168.150.18845nacos2192.168.150.18846nacos3192.168.150…...

编程日记 2023/10/14 6:06:02

运维小工具分享

1.windwos时间同步工具 通过NetTime软件同步 通过一个免费的同步时间软件来进行对时操作 软件官网链接&#xff1a;http://timesynctool.com/ 修改Windows主机时间&#xff0c;修改时间&#xff0c;时间差为10年、3年、4月份、24小时、2小时、1分钟&#xff1b;都可以及时与“…...

编程日记 2023/10/14 6:05:01

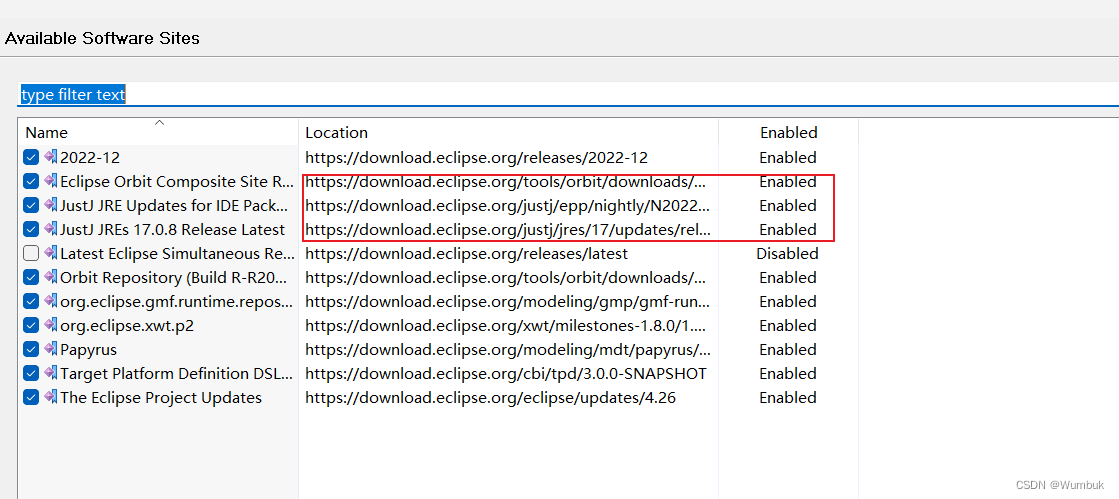
Eclipse插件安装版本不兼容问题解决方案——Papyrus插件为例

项目场景： Eclipse Papyrus安装后，没有新建Papyrus工程选项，也没有新建Papyrus Model的选项。 打开Papyrus Model会报错 问题描述 同样的，安装其他插件也是。可能某个插件之前安装是好用的，结果Eclipse的版本更新了，就再也安装不好用了 原因分析： 根本原因是因为包之…...

编程日记 2023/10/14 6:02:58

【Qt之QTimer】使用及技巧

简介 QTimer是Qt中的定时器类&#xff0c;用于执行定时操作&#xff0c;如在一段时间间隔后触发某个槽函数或执行特定的代码。它提供了灵活的定时功能&#xff0c;可以用于处理各种时间相关的任务。它是基于Qt的事件循环机制工作的。 主要函数说明 构造函数&#xff1a; QTim…...

编程日记 2023/10/14 6:01:57

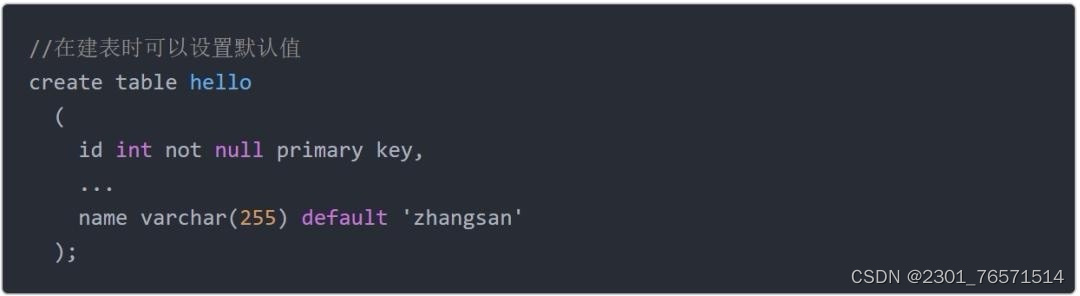
零基础快速自学SQL，2天足矣。

此文是《10周入门数据分析》系列的第6篇。 想了解学习路线&#xff0c;可以先行阅读“ 学习计划 | 10周入门数据分析 ” 上一篇分享了数据库的基础知识&#xff0c;以及如何安装数据库&#xff0c;今天这篇分享数据库操作和SQL。 SQL全称是 Structured Query Language&#x…...

编程日记 2023/10/14 6:00:56

Meta开源数字水印Stable Signature，极大增强生成式AI安全

全球社交、科技巨头Meta&#xff08;Facebook、Instagram等母公司&#xff09;在官网宣布&#xff0c;开源数字水印产品Stable Signature&#xff0c;并公开论文。 据悉&#xff0c;Stable Signature是由Meta和INRIA&#xff08;法国国家信息与自动化研究所&#xff09;联合开…...

编程日记 2023/10/14 5:59:55

python实现分词器

在Python中实现分词有很多方法&#xff0c;具体取决于你的应用场景和数据。下面我会介绍一种常用的分词库——jieba。如果你的数据是英文&#xff0c;你也可以使用nltk库。 中文分词 使用jieba进行中文分词&#xff1a; 首先&#xff0c;你需要安装jieba库。如果还未安装&am…...

编程日记 2023/10/14 5:58:52

【网络】每天掌握一个Linux命令 - iftop

在Linux系统中&#xff0c;iftop是网络管理的得力助手&#xff0c;能实时监控网络流量、连接情况等&#xff0c;帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

编程新知 2025/6/17 9:25:03

（二）TensorRT-LLM | 模型导出（v0.20.0rc3）

0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述&#xff0c;后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作&#xff0c;其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

编程新知 2025/7/2 15:02:24

使用van-uploader 的UI组件，结合vue2如何实现图片上传组件的封装

以下是基于 vant-ui&#xff08;适配 Vue2 版本 &#xff09;实现截图中照片上传预览、删除功能&#xff0c;并封装成可复用组件的完整代码&#xff0c;包含样式和逻辑实现&#xff0c;可直接在 Vue2 项目中使用&#xff1a; 1. 封装的图片上传组件 ImageUploader.vue <te…...

编程新知 2025/6/17 5:20:48

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】

1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件&#xff08;System Property Definition File&#xff09;&#xff0c;用于声明和管理 Bluetooth 模块相…...

编程新知 2025/7/7 19:10:40

Psychopy音频的使用

Psychopy音频的使用 本文主要解决以下问题&#xff1a; 指定音频引擎与设备&#xff1b;播放音频文件 本文所使用的环境&#xff1a; Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

编程新知 2025/7/6 14:54:46

css的定位（position）详解：相对定位 绝对定位 固定定位

在 CSS 中&#xff0c;元素的定位通过 position 属性控制&#xff0c;共有 5 种定位模式&#xff1a;static&#xff08;静态定位&#xff09;、relative&#xff08;相对定位&#xff09;、absolute&#xff08;绝对定位&#xff09;、fixed&#xff08;固定定位&#xff09;和…...

编程新知 2025/7/6 1:55:51

ElasticSearch搜索引擎之倒排索引及其底层算法

文章目录 一、搜索引擎1、什么是搜索引擎？2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长，文件大。2.其次，树深，IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

编程新知 2025/7/7 0:39:27

【Java_EE】Spring MVC

目录 Spring Web MVC ​编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 ​编辑参数重命名 RequestParam ​编辑​编辑传递集合 RequestParam 传递JSON数据 ​编辑RequestBody ​…...

编程新知 2025/7/6 23:44:26

QT： `long long` 类型转换为 `QString` 2025.6.5

在 Qt 中&#xff0c;将 long long 类型转换为 QString 可以通过以下两种常用方法实现&#xff1a; 方法 1&#xff1a;使用 QString::number() 直接调用 QString 的静态方法 number()&#xff0c;将数值转换为字符串&#xff1a; long long value 1234567890123456789LL; …...

编程新知 2025/7/7 18:16:51

OPENCV形态学基础之二腐蚀

一.腐蚀的原理 (图1) 数学表达式&#xff1a;dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一&#xff0c;腐蚀跟膨胀属于反向操作&#xff0c;膨胀是把图像图像变大&#xff0c;而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

编程新知 2025/7/6 16:11:47