力扣刷题 day43:10-13
1.完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
方法一:动态规划
#方法一:动态规划
def numSquares(n):dp=[i for i in range(n+1)] #dp[i] 表示和为i的最小完全平方数for i in range(2,n+1):for j in range(1,int(i**0.5)+1):dp[i]=min(dp[i],dp[i-j*j]+1) #状态转移方程,等于前面数的最小完全平方数加上j*j这个本来就是的即+1return dp[-1]2.最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
方法一:动态规划
#方法一:动态规划
def lengthOfLIS(nums):dp=[1 for i in range(len(nums))] #dp[i] 表示以i位置结尾的最长递增子序列res=0for i in range(len(nums)):for j in range(i):if nums[j]<nums[i]:dp[i]=max(dp[j]+1,dp[i]) #找到之前比当前位置元素小的res=max(res,dp[i])return res3.买卖股票的最佳时机含冷冻期
给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
方法一:动态规划
#方法一:动态规划
def maxProfit(prices):dp0,dp1,dp2=0,float('-inf'),-prices[0] #dp0表示没有股票且不在冷冻期,dp1表示在冷冻期,dp2表示持有股票所得的利益for i in range(1,len(prices)):#dp0下一个状态 #dp1 卖出去了#dp2 要么不卖出去,要么买入dp0,dp1,dp2=max(dp0,dp1),dp2+prices[i], max(dp0 - prices[i],dp2)return max(dp0,dp1,dp2)相关文章:

力扣刷题 day43:10-13
1.完全平方数 给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。 完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 …...

3、在docker 容器中安装tomcat
1、在服务器上查找tomcat镜像,查看前5条 docker search tomcat --limit 5 2、拉取镜像到本地 拉取官方的tomcat到本地 docker pull tomcat:9.0.34-jdk8 3、查看本地镜像 docker images |grep tomcat 4、启动tomcat 服务 使用默认配置 docker ru…...

工业互联网系列1 - 智能制造中有哪些数据在传输
工业互联网以网络为基础,需要传输的数据种类多种多样,这些数据对于实时监控、生产优化、设备维护和决策支持等方面都至关重要。 以下是一些常见智能制造业中需要传输的数据类型: 传感器数据:制造设备上安装的传感器(如…...
centos7部署Nginx和RabbitMQ
文章目录 Nginx安装部署【简单】简介安装 RabbitMQ安装部署【简单】简介安装 Nginx安装部署【简单】 简介 Nginx (engine x) 是一个高性能的HTTP和反向代理web服务器,同时也提供了IMAP/POP3/SMTP服务。Nginx可以托管用户编写的WEB应用程序成为可访问的网页服务&am…...
Nacos集群搭建
Nacos集群搭建 1.集群结构图 Nacos集群图: 其中包含3个nacos节点,然后一个负载均衡器代理3个Nacos。这里负载均衡器可以使用nginx。 三个nacos节点的地址: 节点ipportnacos1192.168.150.18845nacos2192.168.150.18846nacos3192.168.150…...
运维小工具分享
1.windwos时间同步工具 通过NetTime软件同步 通过一个免费的同步时间软件来进行对时操作 软件官网链接:http://timesynctool.com/ 修改Windows主机时间,修改时间,时间差为10年、3年、4月份、24小时、2小时、1分钟;都可以及时与“…...
Eclipse插件安装版本不兼容问题解决方案——Papyrus插件为例
项目场景: Eclipse Papyrus安装后,没有新建Papyrus工程选项,也没有新建Papyrus Model的选项。 打开Papyrus Model会报错 问题描述 同样的,安装其他插件也是。可能某个插件之前安装是好用的,结果Eclipse的版本更新了,就再也安装不好用了 原因分析: 根本原因是因为包之…...

【Qt之QTimer】使用及技巧
简介 QTimer是Qt中的定时器类,用于执行定时操作,如在一段时间间隔后触发某个槽函数或执行特定的代码。它提供了灵活的定时功能,可以用于处理各种时间相关的任务。它是基于Qt的事件循环机制工作的。 主要函数说明 构造函数: QTim…...
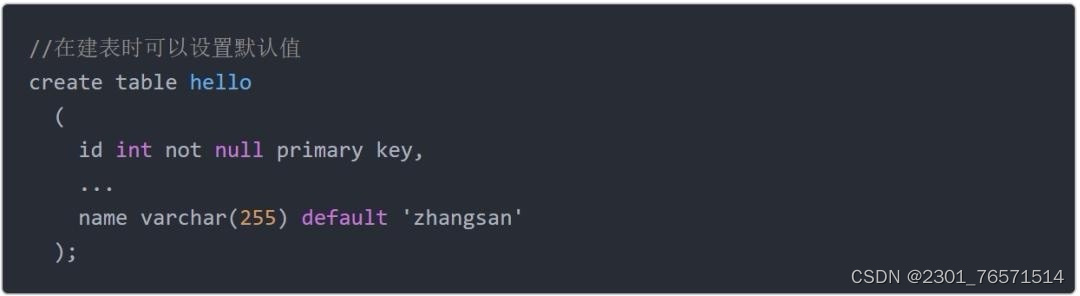
零基础快速自学SQL,2天足矣。
此文是《10周入门数据分析》系列的第6篇。 想了解学习路线,可以先行阅读“ 学习计划 | 10周入门数据分析 ” 上一篇分享了数据库的基础知识,以及如何安装数据库,今天这篇分享数据库操作和SQL。 SQL全称是 Structured Query Language&#x…...

Meta开源数字水印Stable Signature,极大增强生成式AI安全
全球社交、科技巨头Meta(Facebook、Instagram等母公司)在官网宣布,开源数字水印产品Stable Signature,并公开论文。 据悉,Stable Signature是由Meta和INRIA(法国国家信息与自动化研究所)联合开…...

python实现分词器
在Python中实现分词有很多方法,具体取决于你的应用场景和数据。下面我会介绍一种常用的分词库——jieba。如果你的数据是英文,你也可以使用nltk库。 中文分词 使用jieba进行中文分词: 首先,你需要安装jieba库。如果还未安装&am…...
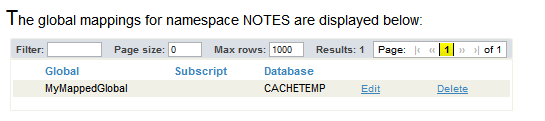
第五十二章 学习常用技能 - Global 映射
文章目录 第五十二章 学习常用技能定义数据库定义命名空间Global映射 第五十二章 学习常用技能 定义数据库 创建本地数据库: 登录管理门户。选择系统管理 > 配置 > 系统配置 > 本地数据库。选择创建新数据库以打开数据库向导。输入新数据库的以下信息&a…...

vue实现瀑布流
1、在 src 目录下创建 component文件夹,在文件夹中创建 vue文件。 2、在 Vue文件中写入以下内容 <div class"pubu"><div class"left"><div class"pubu-item" v-for"item in left" :key"item.id"…...
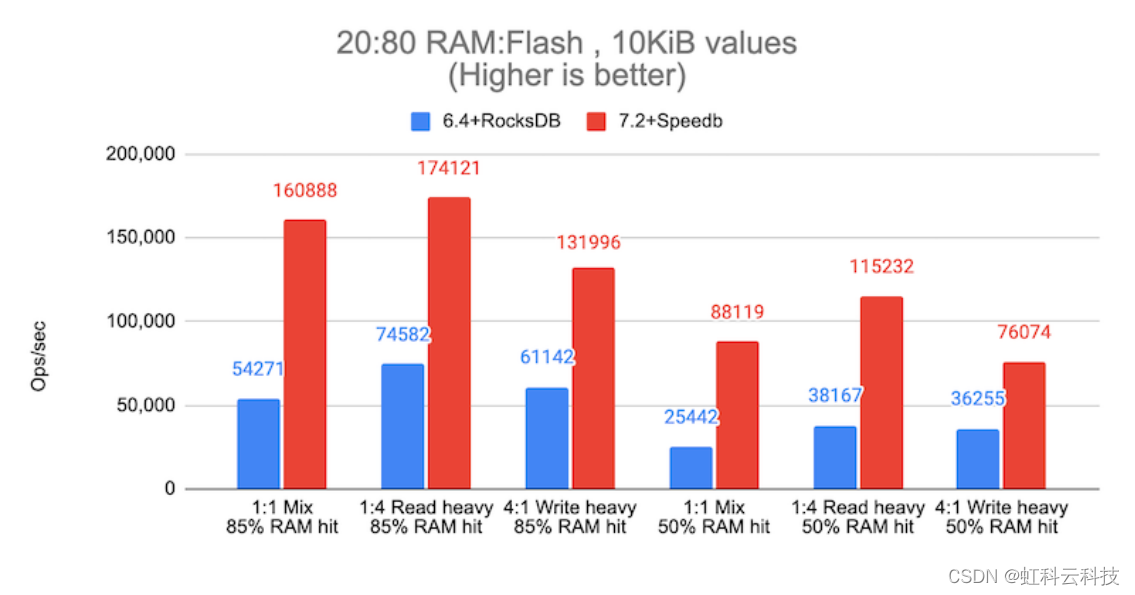
【虹科干货】Redis Enterprise 自动分层技术:大数据集高性能解决方案
越来越多的应用程序依赖于庞大的数据集合,而这些应用程序必须快速响应。借助自动分层,Redis Enterprise 7.2 帮助开发人员轻松创建超快的应用程序。何乐而不为? Redis将数据存储在内存中,因此应用程序能以最快的速度检索和处理数…...

代码随想录训练营二刷第五十四天 | 300.最长递增子序列 674. 最长连续递增序列 718. 最长重复子数组
代码随想录训练营二刷第五十四天 | 300.最长递增子序列 674. 最长连续递增序列 718. 最长重复子数组 一、300.最长递增子序列 题目链接:https://leetcode.cn/problems/longest-increasing-subsequence/ 思路:定义dp[i]表示从0到i的闭区间的最长子序列长…...

LeetCode 2562. 找出数组的串联值【数组,相向双指针】1259
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

SpringBoot使用的时间与空间计量单位
SpringBoot支持JDK8提供的时间与空间计量单位 //时间单位DurationUnit(ChronoUnit.MINUTES)private Duration serverTimeOut;//存储空间单位DataSizeUnit(DataUnit.MEGABYTES)private DataSize dataSize; 在springboot中的具体使用: Component Data ConfigurationPr…...
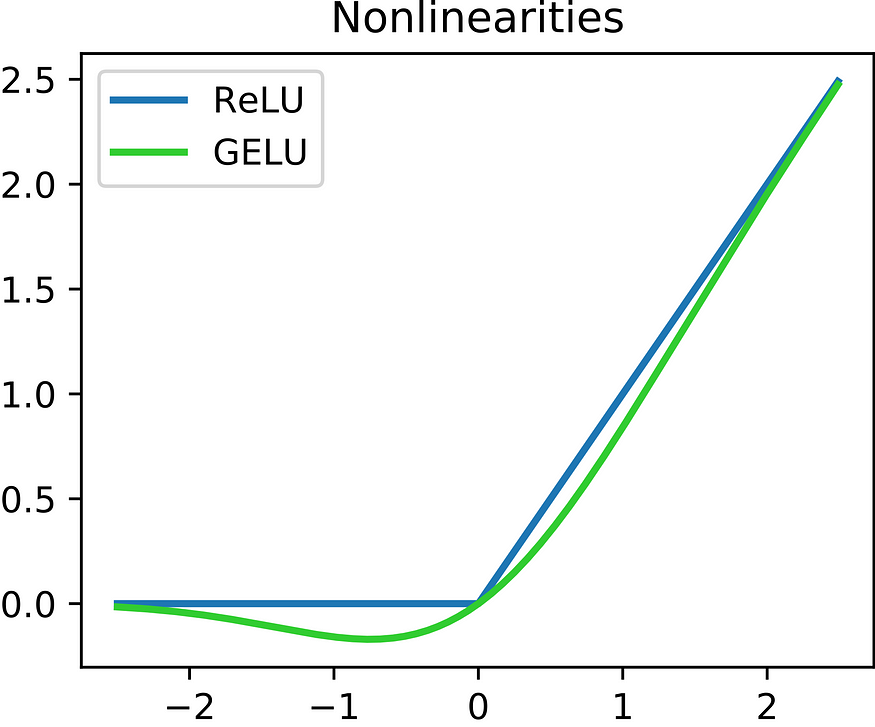
【使用 TensorFlow 2】02/3 使用 Lambda 层创建自定义激活函数
一、说明 TensorFlow 2发布已经接近2年时间,不仅继承了Keras快速上手和易于使用的特性,同时还扩展了原有Keras所不支持的分布式训练的特性。3大设计原则:简化概念,海纳百川,构建生态.这是本系列的第三部分,…...

docker--使用docker login 报错解决方案
我们在本地使用 docker login 命令登录时报错,可以尝试一下先 docker logout 命令退出登录后,在使用 docker login命令进行登录操作; docker logout...
leetcode oj
150. 逆波兰表达式求值 - 力扣(LeetCode) 思路:定义一个名为 Solution 的类,并在其中定义了一个名为 evalRPN 的公共函数。这个函数接受一个由字符串组成的向量 tokens 作为输入,并返回一个整数。 在代码中࿰…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
