【重拾C语言】十、递归程序设计
目录
前言
十、递归程序设计
10.1 计算n!——递归程序设计
10.2 程序设计实例
10.2.1 汉诺塔
10.2.2 齿轮
10.2.3 组合
10.3 计算算术表达式的值——间接递归
10.4 递归程序执行过程
前言
递归程序设计是一种编程技术,其中一个函数通过调用自身来解决问题。递归的思想是将大问题划分为更小的子问题,并通过解决子问题来解决原始问题。递归可以在问题的规模较小的情况下,通过不断地调用自身来解决更大规模的问题。递归函数通常包含两个部分:基本情况和递归情况。
- 基本情况是指问题的规模已经足够小,不再需要进一步的递归调用,可以直接返回结果。这是递归的结束条件。
- 递归情况是指问题的规模仍然较大,需要通过调用自身来解决更小规模的子问题。递归函数在解决子问题时,会不断地调用自身,直到达到基本情况。
十、递归程序设计
10.1 计算n!——递归程序设计
要计算n的阶乘(n!),可以使用递归程序设计。递归计算n的阶乘的思路如下:
- 基本情况:当n为0或1时,阶乘的结果为1。
- 递归情况:当n大于1时,n的阶乘可以表示为n乘以(n-1)的阶乘。
#include <stdio.h>int factorial(int n) {if (n == 0) {return 1;} else {return n * factorial(n - 1);}
}int main() {int n = 5;int result = factorial(n);printf("%d! = %d\n", n, result);return 0;
}函数factorial是递归函数。它将问题划分为计算n乘以(n-1)的阶乘的子问题,并通过递归调用自身来解决子问题,直到达到基本情况。调用这个函数来计算任意正整数n的阶乘,例如factorial(5)将返回120。
10.2 程序设计实例
10.2.1 汉诺塔
汉诺塔是一个经典的递归问题。它涉及将一堆盘子从一个柱子移动到另一个柱子,每次只能移动一个盘子,并且大盘子不能放在小盘子上面。下面是一个用C语言实现汉诺塔问题的递归函数:
#include <stdio.h>void hanoi(int n, char source, char destination, char auxiliary) {if (n == 1) {printf("Move disk 1 from %c to %c\n", source, destination);return;}hanoi(n - 1, source, auxiliary, destination);printf("Move disk %d from %c to %c\n", n, source, destination);hanoi(n - 1, auxiliary, destination, source);
}int main() {int n = 3;hanoi(n, 'A', 'C', 'B');return 0;
} 函数hanoi用来解决汉诺塔问题。它接受四个参数:n表示盘子的数量,source表示源柱子,destination表示目标柱子,auxiliary表示辅助柱子。当n为1时,直接将盘子从源柱子移动到目标柱子。否则,它将递归地将n-1个盘子从源柱子移动到辅助柱子,然后将第n个盘子从源柱子移动到目标柱子,最后将n-1个盘子从辅助柱子移动到目标柱子。
10.2.2 齿轮
10.2.3 组合
组合是数学中的一个概念,指的是从一个给定的集合中选取一部分元素的方式。想要实现一个计算组合的程序,可以使用递归或迭代的方法:
#include <stdio.h>int combination(int n, int k) {if (k == 0 || k == n) {return 1;} else {return combination(n - 1, k - 1) + combination(n - 1, k);}
}int main() {int n = 5;int k = 3;int result = combination(n, k);printf("C(%d, %d) = %d\n", n, k, result);return 0;
} 函数combination用来计算组合。它接受两个参数:n和k,分别表示集合的大小和选取的元素个数。当k等于0或k等于n时,返回1,表示只有一种选取方式。否则,它将递归地计算从n-1个元素中选取k-1个元素的组合数,以及从n-1个元素中选取k个元素的组合数,并将它们相加作为结果。
10.3 计算算术表达式的值——间接递归
要计算算术表达式的值,可以使用间接递归来实现,间接递归是指多个函数之间相互调用形成的递归关系:
#include <stdio.h>int expression_value(char* expression);int factor_value(char* expression) {if (expression[0] == '(') {return expression_value(expression + 1);} else {return expression[0] - '0';}
}int term_value(char* expression) {int value = factor_value(expression);if (expression[1] == '*') {value *= term_value(expression + 2);}return value;
}int expression_value(char* expression) {int value = term_value(expression);if (expression[1] == '+') {value += expression_value(expression + 2);}return value;
}int main() {char expression[] = "((2*3)+4)";int result = expression_value(expression);printf("Expression value: %d\n", result);return 0;
}- 我们定义了三个函数:
expression_value、term_value和factor_value,它们之间相互调用形成了间接递归。factor_value函数用来计算因子的值,如果因子是一个括号内的表达式,则调用expression_value函数来计算括号内表达式的值;否则,将字符转换为对应的数字。term_value函数用来计算项的值,首先计算第一个因子的值,然后判断后面是否有乘号,并乘以后面的因子的值。expression_value函数用来计算表达式的值,首先计算第一个项的值,然后判断后面是否有加号,并加上后面的项的值。
- 在
main函数中,定义一个算术表达式,并调用expression_value函数来计算表达式的值,并打印结果。

10.4 递归程序执行过程
递归程序的执行过程可以通过堆栈(stack)来理解。当一个函数被调用时,它的局部变量和函数调用的返回地址被压入堆栈。如果函数内部包含递归调用,那么每次递归调用都会将新的局部变量和返回地址压入堆栈。递归的结束条件是达到递归终止条件,此时递归开始回溯,从最后一个递归调用返回到上一个递归调用,然后再返回到更上一层递归调用,直到回到最初的函数调用。
在递归程序执行过程中,每个递归调用都会占用一些内存空间,并且会在堆栈上创建一个新的帧(frame),包含局部变量和返回地址。当递归调用过多时,可能会导致堆栈溢出(stack overflow)的问题,因为堆栈的大小是有限的。
- 注意
- 递归终止条件的设置,否则可能会导致无限递归,使程序陷入死循环。
- 递归程序还需要注意递归的效率,因为递归调用会带来函数调用的额外开销。
相关文章:

【重拾C语言】十、递归程序设计
目录 前言 十、递归程序设计 10.1 计算n!——递归程序设计 10.2 程序设计实例 10.2.1 汉诺塔 10.2.2 齿轮 10.2.3 组合 10.3 计算算术表达式的值——间接递归 10.4 递归程序执行过程 前言 递归程序设计是一种编程技术,其中一个函数通过调用自身…...

SQL日期字段去时分秒
substring( convert(varchar,[申请日期],120),1,10) AS 申请日期 运行结果对比展示 申请日期申请日期2022-12-24 00:00:00.0002022-12-24 说明: substring(...): 这是SQL中用于提取字符串一部分的函数。 convert(varchar, 申请日期, 120): 这部分将日期值&#…...
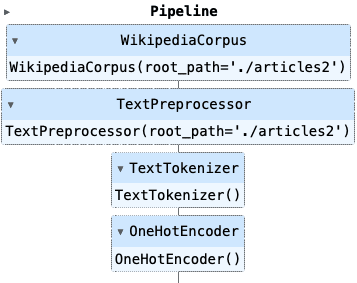
NLP项目:维基百科文章爬虫和分类【02】 - 语料库转换管道
一、说明 我的NLP项目在维基百科条目上下载、处理和应用机器学习算法。相关上一篇文章中,展示了项目大纲,并建立了它的基础。首先,一个 Wikipedia 爬网程序对象,它按名称搜索文章,提取标题、类别、内容和相关页面&…...
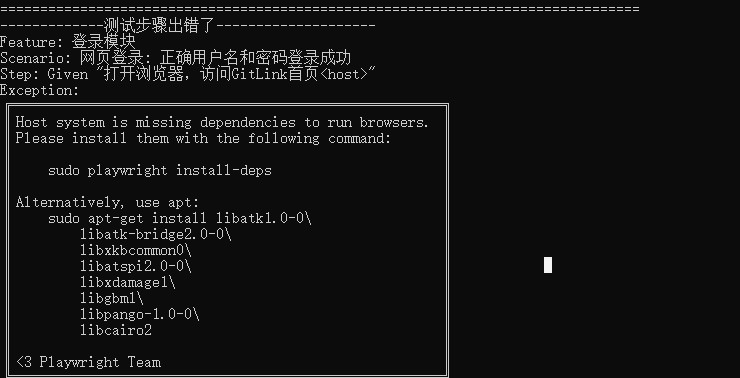
如何在Ubuntu 20.04.6 LTS系统上运行Playwright自动化测试
写在前面 这里以 Ubuntu 20.04.6 LTS为例。示例代码:自动化测试代码。 如果过程中遇到其他非文本中提到的错误,可以使用搜索引擎搜索错误,找出解决方案,再逐步往下进行。 一、 环境准备 1.1 安装python3 1.1.1 使用APT安装Py…...

c++ sort函数cmp比较参数传入
开始 假定有一个结构体 struct node{int p,r,val; };第一种 定义cmp函数,sort直接传入cmp bool cmp(node a,node b){return a.p<b.p;} sort(vec.begin(),vec.end(),cmp);第二种 lamada表达式??这个中括号里面可以不为空,但是…...
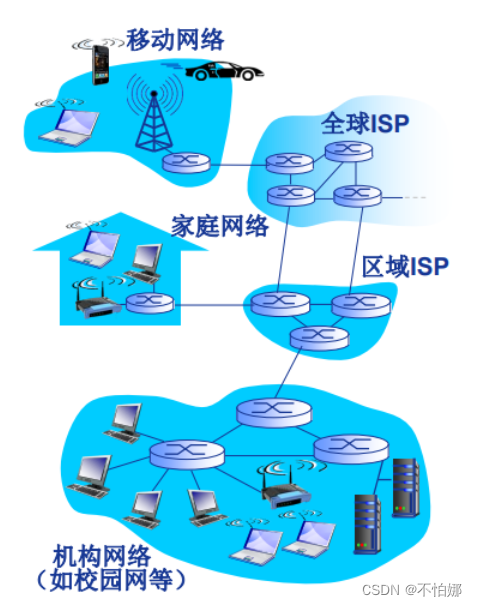
【计算机网络笔记】什么是计算机网络?
前言计算机网络的定义交换网络什么是Internet从组成细节角度看从服务角度看 最后感谢 💖 本篇文章总字数:1342字 预计阅读时间:5~10min 建议收藏之后慢慢阅读 前言 计算机网络通信技术计算机技术。 计算机网络是通信技术与计算机技术紧密结…...

极简C++(2) 类与对象
类与对象的基本概念 CLASS类将数据以及数据上的操作封装在一起 OBJECT对象是有具体类类型的变量 打个比方,类就像一个制作月饼的摸具,那么我们可以通过这个摸具来放入面粉和馅料编程一个月饼,那么摸具就是类,而各种各样的月饼便是…...

【Java 进阶篇】JavaScript流程控制语句详解
JavaScript是一门高级编程语言,具备丰富的流程控制语句,用于控制程序的执行流程。在本篇博客中,我们将深入探讨JavaScript的流程控制语句,包括条件语句、循环语句、以及其他一些控制语句。这篇博客将逐步介绍这些概念,…...
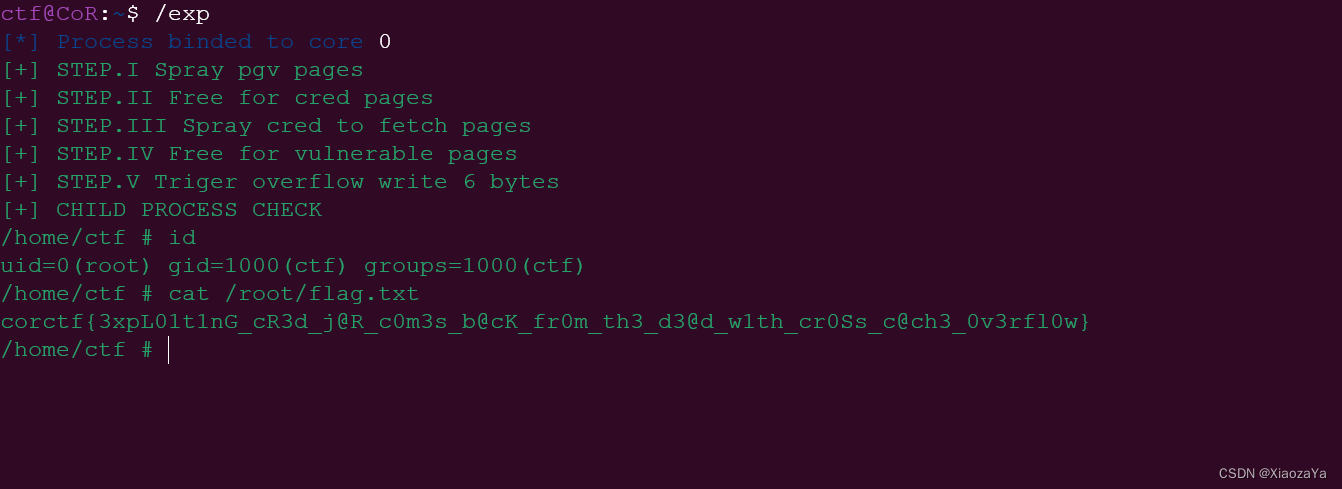
【Page-level Heap Fengshui -- Cross-Cache Overflow】corCTF2022-cache-of-castaways
前言 什么叫 Cross Cache 呢?其实就是字面意思,我们知道内核中的大部分结构体都有自己的专属 slab 内存池。那现在我们可以想象一下这个场景,我们拥有一个特定 kmem-cache 的溢出漏洞,那么我们该如何利用呢? 程序分析…...
vue-mixin
1.vue中,混入(mixin)是一种特殊的使用方式。一个混入对象可以包含任意的组件配置选项(data, props, components, watch,computed…)可以根据需求"封装"一些可复用的单元,并在使用时根据一定的策略合并到组件的选项中,使用时和组件自…...

力扣刷题 day43:10-13
1.完全平方数 给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。 完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 …...

3、在docker 容器中安装tomcat
1、在服务器上查找tomcat镜像,查看前5条 docker search tomcat --limit 5 2、拉取镜像到本地 拉取官方的tomcat到本地 docker pull tomcat:9.0.34-jdk8 3、查看本地镜像 docker images |grep tomcat 4、启动tomcat 服务 使用默认配置 docker ru…...

工业互联网系列1 - 智能制造中有哪些数据在传输
工业互联网以网络为基础,需要传输的数据种类多种多样,这些数据对于实时监控、生产优化、设备维护和决策支持等方面都至关重要。 以下是一些常见智能制造业中需要传输的数据类型: 传感器数据:制造设备上安装的传感器(如…...
centos7部署Nginx和RabbitMQ
文章目录 Nginx安装部署【简单】简介安装 RabbitMQ安装部署【简单】简介安装 Nginx安装部署【简单】 简介 Nginx (engine x) 是一个高性能的HTTP和反向代理web服务器,同时也提供了IMAP/POP3/SMTP服务。Nginx可以托管用户编写的WEB应用程序成为可访问的网页服务&am…...
Nacos集群搭建
Nacos集群搭建 1.集群结构图 Nacos集群图: 其中包含3个nacos节点,然后一个负载均衡器代理3个Nacos。这里负载均衡器可以使用nginx。 三个nacos节点的地址: 节点ipportnacos1192.168.150.18845nacos2192.168.150.18846nacos3192.168.150…...
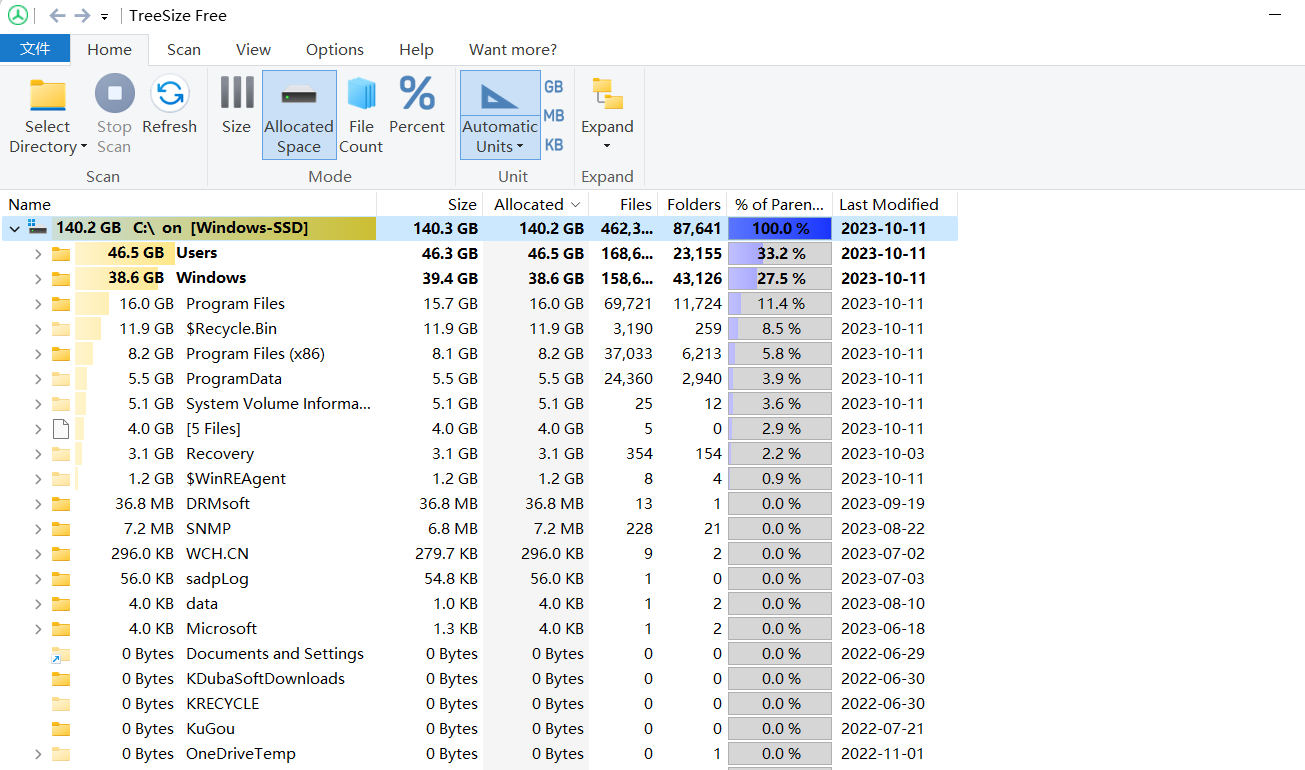
运维小工具分享
1.windwos时间同步工具 通过NetTime软件同步 通过一个免费的同步时间软件来进行对时操作 软件官网链接:http://timesynctool.com/ 修改Windows主机时间,修改时间,时间差为10年、3年、4月份、24小时、2小时、1分钟;都可以及时与“…...
Eclipse插件安装版本不兼容问题解决方案——Papyrus插件为例
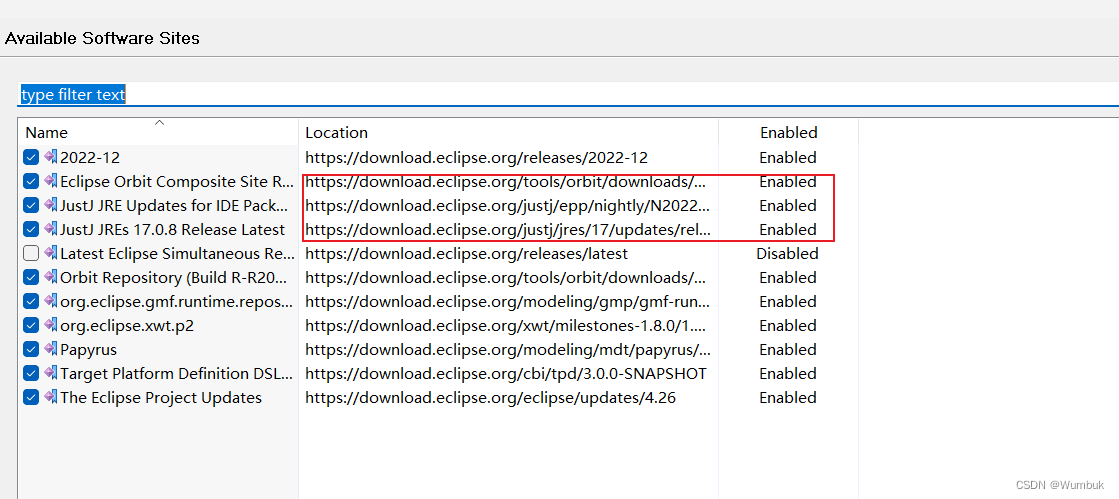
项目场景: Eclipse Papyrus安装后,没有新建Papyrus工程选项,也没有新建Papyrus Model的选项。 打开Papyrus Model会报错 问题描述 同样的,安装其他插件也是。可能某个插件之前安装是好用的,结果Eclipse的版本更新了,就再也安装不好用了 原因分析: 根本原因是因为包之…...

【Qt之QTimer】使用及技巧
简介 QTimer是Qt中的定时器类,用于执行定时操作,如在一段时间间隔后触发某个槽函数或执行特定的代码。它提供了灵活的定时功能,可以用于处理各种时间相关的任务。它是基于Qt的事件循环机制工作的。 主要函数说明 构造函数: QTim…...
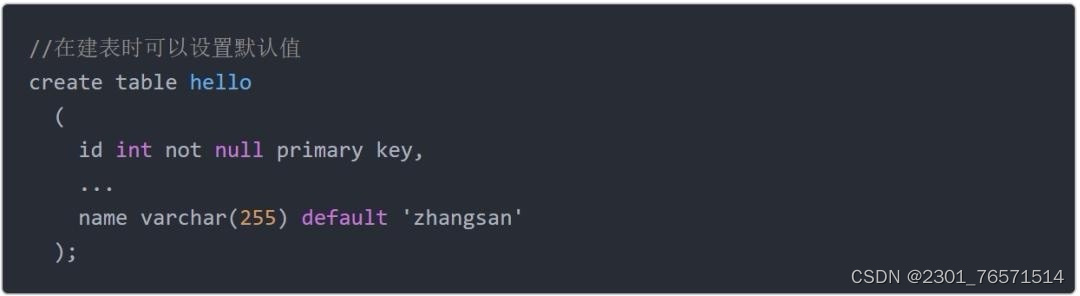
零基础快速自学SQL,2天足矣。
此文是《10周入门数据分析》系列的第6篇。 想了解学习路线,可以先行阅读“ 学习计划 | 10周入门数据分析 ” 上一篇分享了数据库的基础知识,以及如何安装数据库,今天这篇分享数据库操作和SQL。 SQL全称是 Structured Query Language&#x…...

Meta开源数字水印Stable Signature,极大增强生成式AI安全
全球社交、科技巨头Meta(Facebook、Instagram等母公司)在官网宣布,开源数字水印产品Stable Signature,并公开论文。 据悉,Stable Signature是由Meta和INRIA(法国国家信息与自动化研究所)联合开…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
