估算总体标准差的极差均值估计法sigma = R/d2
总体标准差的估算值可以通过将平均极差除以合适的常数因子d2来计算。这个估算方法是用于估算总体标准差的一种常见方法,尤其在质量控制和过程监控中经常使用。
总体标准差的估算值 = (平均极差) / d2
其中:
- "总体标准差的估算值" 表示用极差方法估算的总体标准差。
- "平均极差" 是各个子组的极差的平均值。
- "d2" 是根据采样方法和子组样本容量选择的常数因子,用于校正极差以估算总体标准差。
# 估算整体数据集的标准差
R = np.mean(range_per_group) # 极差均值
d2 = 2.847 # 根据具体的采样方法选择合适的d2值
std = R / d2
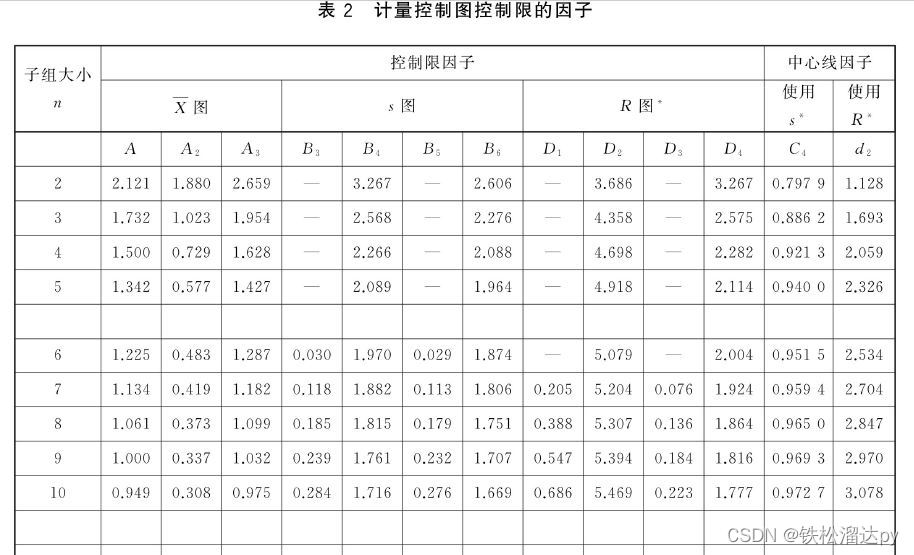
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
plt.rcParams['font.sans-serif'] = ['SimHei'] # 防止中文标签乱码
plt.rcParams['axes.unicode_minus'] = False# 准备数据,这里使用随机数据作为示例
# data = [np.random.randn(8) for _ in range(10)]
data = np.random.randn(8, 8)
# 计算每个分组的极差
range_per_group = [np.ptp(group) for group in data]# 扁平化数据
flat_data = np.concatenate(data)# 计算各组均值的均值
x_bar_avg = np.mean([np.mean(group) for group in data])# 估算整体数据集的标准差
R = np.mean(range_per_group)
d2 = 2.847 # 根据具体的采样方法选择合适的d2值
std = R / d2# 生成正态分布的概率密度曲线,使用各组均值的均值作为中心
x = np.linspace(min(flat_data), max(flat_data), 100)
pdf = norm.pdf(x, loc=x_bar_avg, scale=std)# 绘制直方图
plt.hist(flat_data, bins=8, density=True, alpha=0.5, color='b', label='直方图')# 绘制概率密度曲线
plt.plot(x, pdf, color='r', label='概率密度曲线')# 添加标签和标题
plt.xlabel('X轴标签')
plt.ylabel('Y轴标签')
plt.title('整体数据的直方图和使用各组均值的均值生成的概率密度曲线')# 显示图形
plt.legend()
plt.show()-
X-R 控制图(Individuals and Range Control Chart):
- 通常适用于小样本容量,尤其是子组样本容量小于 10 的情况。
- X-R 控制图是用于监控过程变异性的一种方法,范围(Range,R)用于度量子组内的变异性。
- 适用于较小的子组容量,因为大样本容量的情况下,范围(R)可能会变得相对稳定,难以检测到小幅度的过程变异。
-
X-S 控制图(Individuals and Standard Deviation Control Chart):
- 通常适用于较大的样本容量,尤其是子组样本容量较大的情况。
- X-S 控制图用于监控过程的稳定性,标准差(Standard Deviation,S)用于度量子组内的变异性。
- 适用于较大的样本容量,因为在小样本容量情况下,估算标准差可能会不够稳定。
总之,X-R 控制图通常用于小样本容量,而 X-S 控制图更适用于较大的样本容量,因为它们分别适应不同的过程变异性度量方法。选择哪种控制图取决于您的具体应用和数据情况,以确保有效地监控过程的稳定性和变异性。
----------------------------------
控制图(如X-R图和X-S图)是一种用于估算总体标准差的方法,通常应用于质量控制和过程监控。这些方法利用过程中的变异性来估算总体标准差。
具体来说:
-
X-R 图(Individuals and Range Control Chart):在X-R图中,X图用于监测过程的平均值,而R图用于监测子组样本的极差。通过监控这两个图,您可以估算过程的总体标准差。总体标准差的估算方法如下:
总体标准差的估算值 = R图的平均极差 / d2
这里,R图的平均极差是R图中各个子组极差的平均值,d2是一个根据样本容量选择的常数因子。
-
X-S 图(Individuals and Standard Deviation Control Chart):在X-S图中,X图用于监测过程的平均值,而S图用于监测子组样本的标准差。通过监控这两个图,您可以估算过程的总体标准差。总体标准差的估算方法如下:
总体标准差的估算值 = S图的平均标准差 / c4
这里,S图的平均标准差是S图中各个子组标准差的平均值,c4是一个根据样本容量选择的常数因子。
这两种控制图方法能够提供过程的实时监测和总体标准差的估算,有助于及时发现和纠正过程中的变异性。它们在质量控制和过程改进中发挥着重要的作用。
| 1组 | 2组 | 3组 | 4组 | 5组 | 6组 | 7组 | 8组 | 9组 | 10组 | 11组 | 12组 |
| 6.4 | 6.8 | 6.3 | 6.1 | 6.4 | 6.6 | 6.3 | 6.4 | 6.3 | 6.7 | 6.6 | 6.8 |
| 7.0 | 6.4 | 7.1 | 6.8 | 6.9 | 6.0 | 6.9 | 5.6 | 6.7 | 5.9 | 7.0 | 6.2 |
| 6.4 | 6.4 | 6.5 | 5.9 | 6.8 | 6.1 | 6.6 | 6.2 | 6.6 | 5.8 | 6.5 | 6.5 |
| 6.4 | 6.3 | 6.4 | 5.8 | 6.5 | 6.2 | 6.2 | 6.0 | 6.4 | 6.3 | 6.4 | 6.2 |
| 7.1 | 6.5 | 7.0 | 6.0 | 6.9 | 5.9 | 6.8 | 5.8 | 6.3 | 6.2 | 7.1 | 5.8 |
相关文章:

估算总体标准差的极差均值估计法sigma = R/d2
总体标准差的估算值可以通过将平均极差除以合适的常数因子d2来计算。这个估算方法是用于估算总体标准差的一种常见方法,尤其在质量控制和过程监控中经常使用。 总体标准差的估算值 (平均极差) / d2 其中: "总体标准差的估算值" 表示用极差…...

JavaScript之正则表达式
详见MDN 正则表达式(RegExp) 正则表达式不是JS独有的内容,大部分语言都支持正则表达式 JS中正则表达式使用得不是那么多,我们可以尽量避免使用正则表达式 在JS中,正则表达式就是RegExp对象,RegExp 对象用于将文本与一个模式匹配 正…...

Spring实战 | Spring AOP核心功能分析之葵花宝典
国庆中秋特辑系列文章: 国庆中秋特辑(八)Spring Boot项目如何使用JPA 国庆中秋特辑(七)Java软件工程师常见20道编程面试题 国庆中秋特辑(六)大学生常见30道宝藏编程面试题 国庆中秋特辑&…...

linux之/etc/skel目录
/etc/skel目录是在使用useradd添加用户时,一个需要用到的目录,该目录用来存放新建用户时需要拷贝到新建用户家目录下的文件。即:当我们新建新用户时,这个目录下的所有文件会自动被复制到新建用户的家目录下,默认情况下…...

文件介绍---C语言编程
0 Preface/Foreword 1 C文件概述 文件(File)是程序设计中的一个重要的概念。所谓“文件”一般指存储在外部介质上数据的集合。一批数据是以文件的形式存放在外部介质(如磁盘)上。操作系统是以文件为单位对数据进行管理,…...
)
软考 系统架构设计师系列知识点之特定领域软件体系结构DSSA(6)
接前一篇文章:软考 系统架构设计师系列知识点之特定领域软件体系结构DSSA(5) 所属章节: 第7章. 系统架构设计基础知识 第5节. 特定领域软件体系结构 相关试题 3. 特定领域软件架构(Domain Specific Software Archite…...
TensorFlow入门(二十三、退化学习率)
学习率 学习率,控制着模型的学习进度。模型训练过程中,如果学习率的值设置得比较大,训练速度会提升,但训练结果的精度不够,损失值容易爆炸;如果学习率的值设置得比较小,精度得到了提升,但训练过程会耗费太多的时间,收敛速度慢,同时也容易出现过拟合的情况。 退化学习率 退化学…...
登录中获取验证码的节流
一. 验证码框 <el-input placeholder"请输入验证码" prefix-icon"el-icon-lock" v-model"ruleForm.code"><el-button slot"suffix" :disabled"disabled" type"text" size"mini" click"ch…...

spring boot 实现Minio分片上传
应用场景 分片上传,就是将所要上传的文件,按照一定的大小,将整个文件分隔成多个数据块(我们称之为Part)来进行分别上传,上传完之后再由服务端对所有上传的文件进行汇总整合成原始的文件。 分片上传的场景…...

2023年09月 C/C++(六级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C编程(1~8级)全部真题・点这里 Python编程(1~6级)全部真题・点这里 第1题:生日相同 在一个有180人的大班级中,存在两个人生日相同的概率非常大,现给出每个学生的名字,出生月日。试…...

docker-compose 部署示例
文章目录 docker-compose文件格式docker-compose 下载 docker-compose文件格式 这个软件的实际很小,只是根据配置文件产生一些docker命令来执行可以。 配置文件本身是yml的格式,如下 version: 3.5services:# Etherpad: real-time collaborative docume…...

新版WordPress插件短视频去水印小程序源码
最新版去水印小程序源码,本版本全开源,是WordPress插件 上传到Wordpress 安装插件 启动之后 绑定自己的小程序id wordpress可以在宝塔一键部署 也可以用我的这个 搭建前我们需要一下东西: 第一个:一台服务器(国内外都可…...

如何提高MES系统的落地成功率?
导 读 ( 文/ 2768 ) 制造执行系统(MES)在现代制造业中扮演着至关重要的角色,但实施MES系统并取得成功并非易事。为了帮助企业提高MES系统的落地成功率,本文将介绍关键的方法和策略。通过深入了解业务需求、有效的团队合作、全面的…...
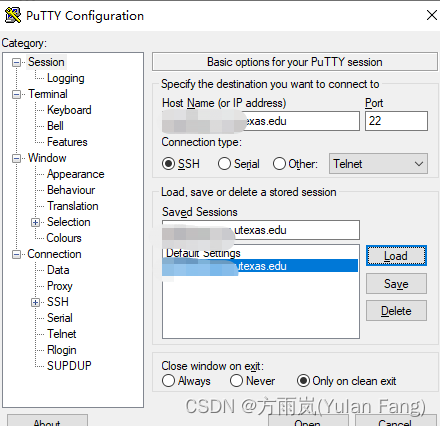
private key ssh连接服务器
这里用到的软件是PuTTY。 https://www.chiark.greenend.org.uk/~sgtatham/putty/latest.html 保存本地rsa文件后,打开软件PuTTYgen,点击Load导入文件,输入Key passphrase即密码,保存至本地。 随后在PuTTY配置ssh的用户名 来Cred…...

PDF-Word-图片等的互相转换
轻闪PDF客户端 - 功能强大的一站式PDF工具 | PDF编辑、转换、阅读 上面页面支持PDF转换成各类别:鼠标停留在PDF工具,点击转换类型即可在线转换 Word-PDF:word文档打开word文件中,点击文件->另存为->另存为的位置->保存…...

【VR开发】【Unity】0-课程简介和概述
【说明】 这是我录制的一套VR基础开发课程的文字版本,更加便于快速参考。 应大家在后台所提的需求,从今天开始,我计划带给大家一套完整达40课时的VR开发基础课程。 在开始学习前需要注意如下几点: 本教程基于Unity2022.2.1f1版…...
)
Java面试题-Java核心基础-第三天(基本数据类型)
目录 一、Java的基本数据类型了解吗? 二、基本类型和包装类型的区别 三、包装类型的缓存机制了解吗? 四、自动拆箱和自动装箱了解吗? 五、为什么浮点数在运算的时候会有精度损失的风险? 六、如何解决浮点数在运算时存在的精度…...
)
Bean容器里的单例是根据什么识别它是同一个类呢?(比如容器里创建了A类,再去用这个A类的时候,Bean容器怎么知道这个就是A类?)
Spring容器中的Bean的识别主要依赖于Bean的名称(ID)和类型。以下是详细解释: Bean的名称(ID):每个Bean在Spring容器中都必须有一个唯一的名称(ID)。这个名称通常在配置文件中、Java…...

简述 happens - before 八大规则
“Happens-Before” 是Java内存模型中的概念,用于描述多线程程序中操作之间的顺序和可见性关系。它定义了一组规则,哪些操作具有可预测的行为。以下是"Happens-Before" 的八大规则: 程序顺序规则(Program Order Rule&am…...

windows flask 多进程高并发
最近在做的一个项目,需要将十几个python函数封装程flask服务供外界调用,每个函数之间没有什么关系,相互独立。虽然感觉不是很难,但因为用的windows系统,遇到的坑比较多,在此一一总结一下。 flask偶尔出现卡…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
