LCR 095. 最长公共子序列(C语言+动态规划)
1. 题目
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
2. 输入输出样例
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc" ,它的长度为 3 示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0 。提示:
1 <= text1.length, text2.length <= 1000text1和text2仅由小写英文字符组成。
3. 解题思想
动态规划步骤:
(1)dp状态:
dp[i][j]表示以text1[i]、text2[j]为结尾的两个字符串中最长公共子序列的长度;
(2)状态转移方程:
text1[i] == text2[j]:dp[i][j] = dp[i - 1][j - 1] + 1;
text1[i] != text2[j]:max(dp[i - 1][j], dp[i][j - 1]);
(3)初始化状态:
第0行第0列:text1[0] == text2[0]:dp[0][0] = 1;text1[0] != text2[0]:dp[0][0] = 0;
第0行:text1[i] == text2[0]:dp[i][0] = 1;text1[i] != text2[0]:dp[i][0] = dp[i - 1][0];
第0列:text1[0] == text2[i]:dp[0][1] = 1;text1[0] != text2[i]:dp[0][i] = dp[0][i-1];
(4)最优解:
dp[n-1][m-1] ;
算法描述:
核心思想是通过填充 dp 数组,逐步构建最长公共子序列的长度,考虑字符是否匹配。
- 首先,获取输入字符串
text1和text2的长度,并创建一个二维数组dp,其大小为(n+1) x (m+1),其中n和m分别是两个字符串的长度。dp[i][j]表示text1的前i个字符和text2的前j个字符的最长公共子序列的长度。- 初始化
dp数组的第一行和第一列:遍历两个字符串的首字符,如果它们相等,将dp[0][0]设置为1,否则将其保留为0。接着,初始化第一行和第一列的其余部分,以表示以text1[0]或text2[0]开头的子序列。- 使用两个嵌套循环遍历
text1和text2的每个字符(除去第一个字符),填充dp数组。如果当前字符相同(text1[i] == text2[j]),则将dp[i][j]设置为左上角的对角元素值加1,表示找到了一个更长的公共子序列。如果当前字符不同,将dp[i][j]设置为左边或上边的较大值,表示要么继承左边的最长子序列长度,要么继承上边的最长子序列长度。- 最终,
dp[n-1][m-1]中存储的值即为text1和text2的最长公共子序列的长度。
4. 代码实现
// 定义一个函数,该函数返回两个整数指针中的较大值
int max_(int *a, int *b) {// 比较两个指针的值,返回较大的指针if (a > b) {return a;}return b;
}// 定义一个计算两个字符串的最长公共子序列的函数
int longestCommonSubsequence(char *text1, char *text2) {// 获取字符串text1和text2的长度int n = strlen(text1);int m = strlen(text2);// 创建一个二维数组dp,用于存储最长公共子序列的长度int dp[n][m];// 初始化dp数组,将所有元素设置为0for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {dp[i][j] = 0;}}// 初始化dp数组的第一个元素if (text1[0] == text2[0]) {dp[0][0] = 1;}// 处理第一列,初始化以text1[0]为开头的子序列for (int i = 1; i < n; i++) {if (text1[i] == text2[0]) {dp[i][0] = 1;} else {dp[i][0] = dp[i - 1][0];}}// 处理第一行,初始化以text2[0]为开头的子序列for (int i = 1; i < m; i++) {if (text1[0] == text2[i]) {dp[0][i] = 1;} else {dp[0][i] = dp[0][i - 1];}}// 填充dp数组的其余部分,找到最长公共子序列的长度for (int i = 1; i < n; i++) {for (int j = 1; j < m; j++) {if (text1[i] == text2[j]) {// 如果字符相同,将dp[i][j]设置为左上角值加1dp[i][j] = dp[i - 1][j - 1] + 1;} else {// 如果字符不相同,将dp[i][j]设置为左边和上边的较大值dp[i][j] = max_(dp[i - 1][j], dp[i][j - 1]);}}}// 返回dp数组的最右下角元素,即最长公共子序列的长度return dp[n - 1][m - 1];
}
5. 复杂度分析
时间复杂度分析:
- 初始化
dp数组的两个嵌套循环(for循环嵌套)需要遍历整个数组,时间复杂度为O(n * m),其中 n 和 m 分别是text1和text2的长度。- 接下来,还需要一个嵌套循环来填充
dp数组,这个循环也需要遍历整个dp数组,时间复杂度为O(n * m)。- 总的时间复杂度是O(n * m + n * m),即O(n * m)。
算法的时间复杂度是 O(n * m),其中 n 和 m 分别是输入字符串 text1 和 text2 的长度。
空间复杂度分析:
dp数组的空间复杂度是O(n * m),因为它是一个二维数组,其大小与输入字符串的长度相关。
综上所述,这段代码的空间复杂度是 O(n * m),时间复杂度是 O(n * m)
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台![]() https://leetcode.cn/problems/qJnOS7/submissions/
https://leetcode.cn/problems/qJnOS7/submissions/
相关文章:
LCR 095. 最长公共子序列(C语言+动态规划)
1. 题目 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。 一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(…...

程序员不写注释:探讨与反思
一、为什么程序员不写注释 当程序员选择不写注释时,通常有一系列常见原因,这些原因可以影响他们的决策和行为。同时,这个决策可能会带来多方面的影响和后果。以下是详细阐述为什么程序员不写注释的常见原因以及这种决策可能导致的影响和后果…...
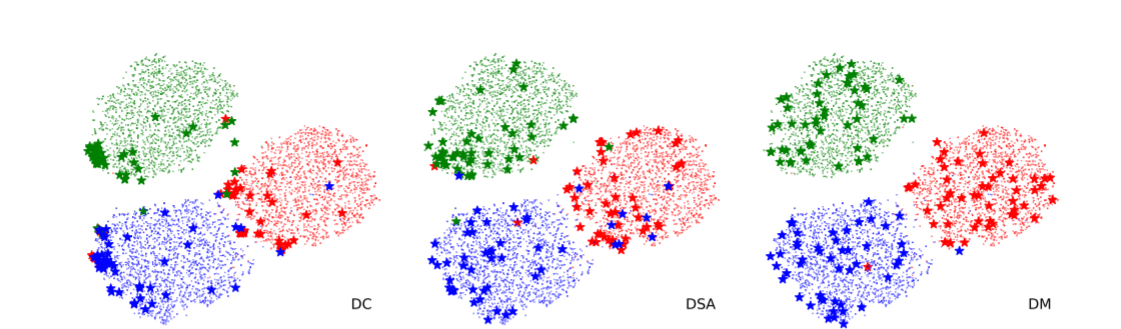
《论文阅读:Dataset Condensation with Distribution Matching》
点进去这篇文章的开源地址,才发现这篇文章和DC DSA居然是一个作者,数据浓缩写了三篇论文,第一篇梯度匹配,第二篇数据增强后梯度匹配,第三篇匹配数据分布。DC是匹配浓缩数据和原始数据训练一次后的梯度差,DS…...
免费chatGPT工具
发现很多人还是找不到好用的chatGPT工具,这里分享一个邮箱注册即可免费试用。 PromptsZone - 一体化人工智能平台使用 PromptsZone 与 ChatGPT、Claude、AI21 Labs、Google Bard 聊天,并使用 DALL-E、Stable Diffusion 和 Google Imagegen 创建图像&…...

数据分析基础:数据可视化+数据分析报告
数据分析是指通过对大量数据进行收集、整理、处理和分析,以发现其中的模式、趋势和关联,并从中提取有价值的信息和知识。 数据可视化和数据分析报告是数据分析过程中非常重要的两个环节,它们帮助将数据转化为易于理解和传达的形式࿰…...

settings.xml的文件配置大全
settings.xml 文件中最常配置的还是这几个标签 localRepository和mirrors settings.xml文件官方文档地址 <settings xmlns"http://maven.apache.org/SETTINGS/1.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"ht…...
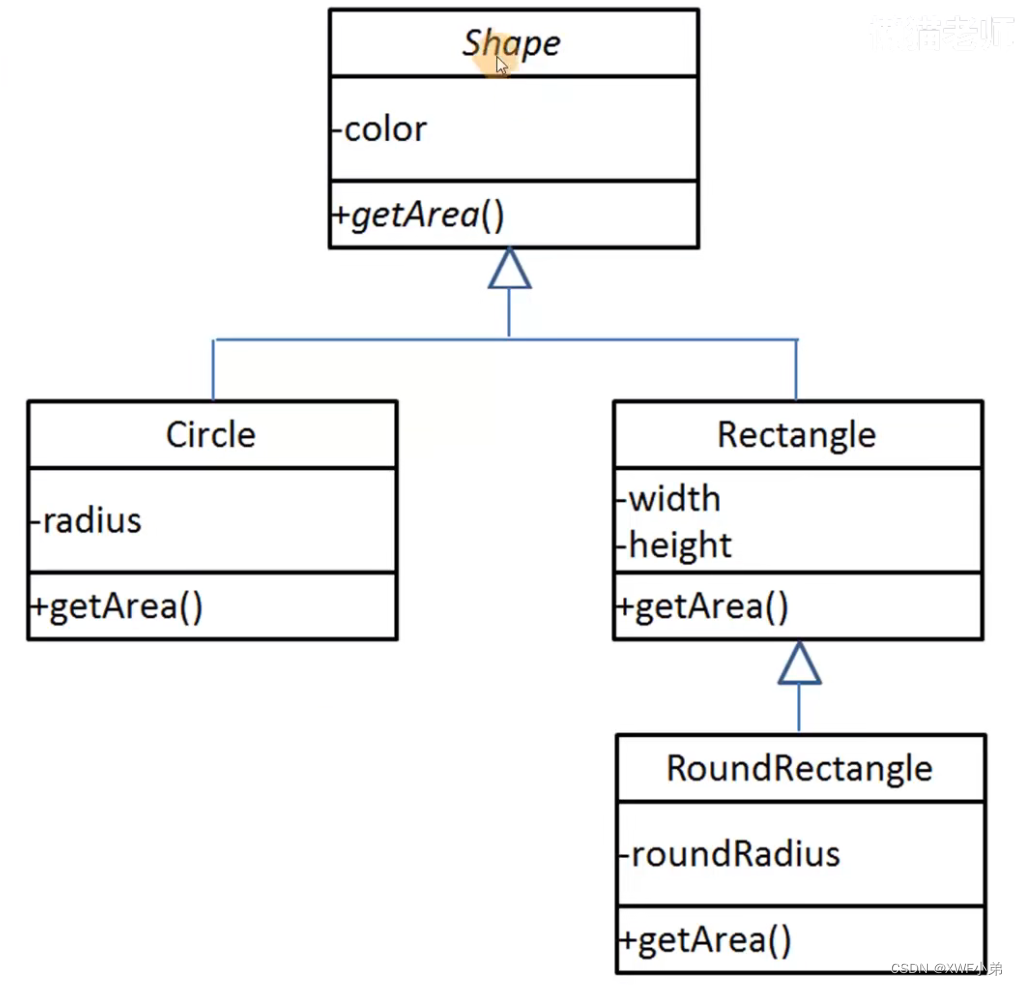
极简c++(7)类的继承
为什么要用继承 子类不必复制父类的任何属性,已经继承下来了;易于维护与编写; 类的继承与派生 访问控制规则 一般只使用Public! 构造函数的继承与析构函数的继承 构造函数不被继承! 在创建子类对象的时候&…...
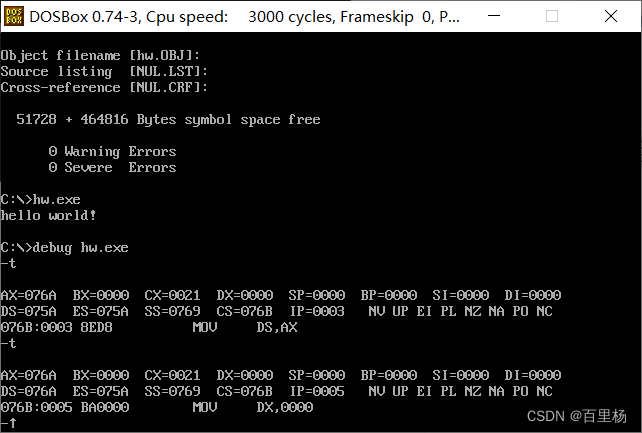
DOSBox和MASM汇编开发环境搭建
DOSBox和MASM汇编开发环境搭建 1 安装DOSBox2 安装MASM3 编译测试代码4 运行测试代码5 调试测试代码 本文属于《 X86指令基础系列教程》之一,欢迎查看其它文章。 1 安装DOSBox 下载DOSBox和MASM:https://download.csdn.net/download/u011832525/884180…...
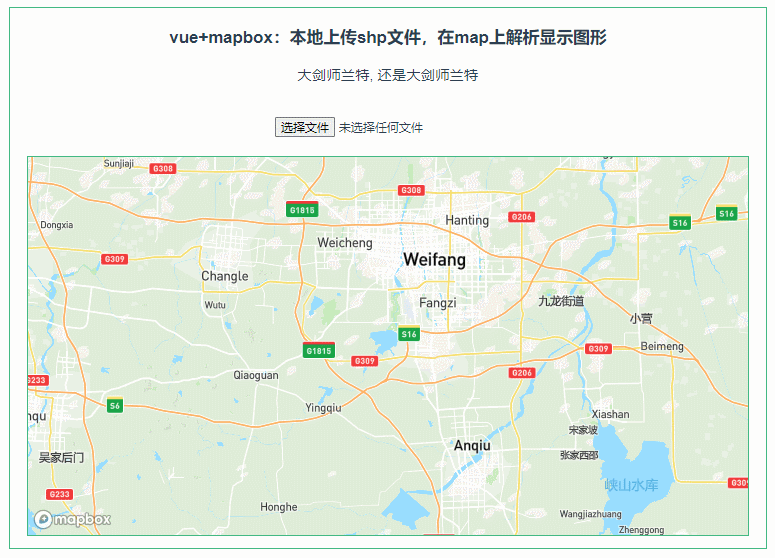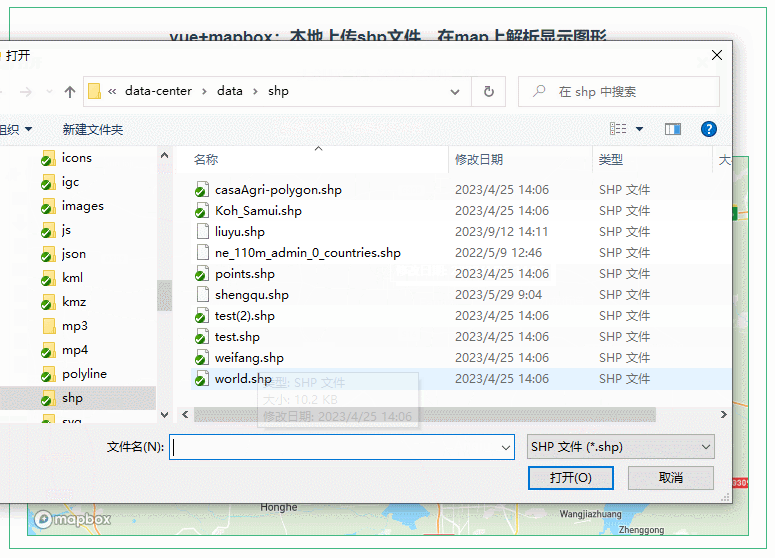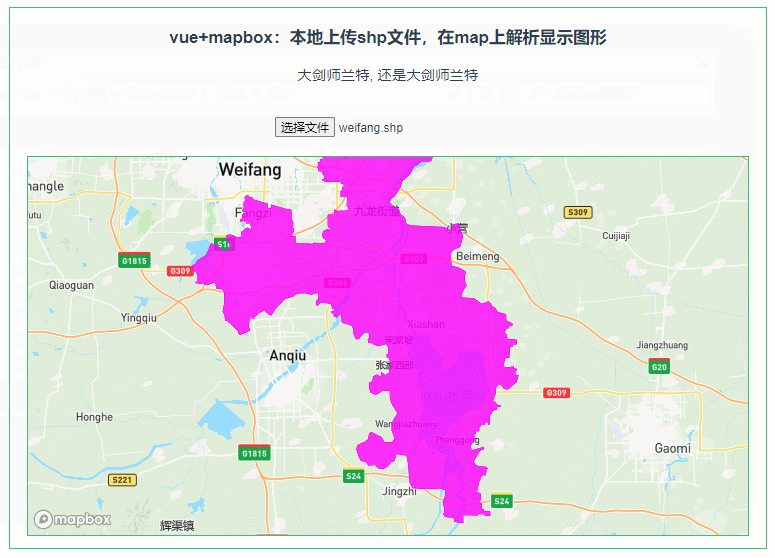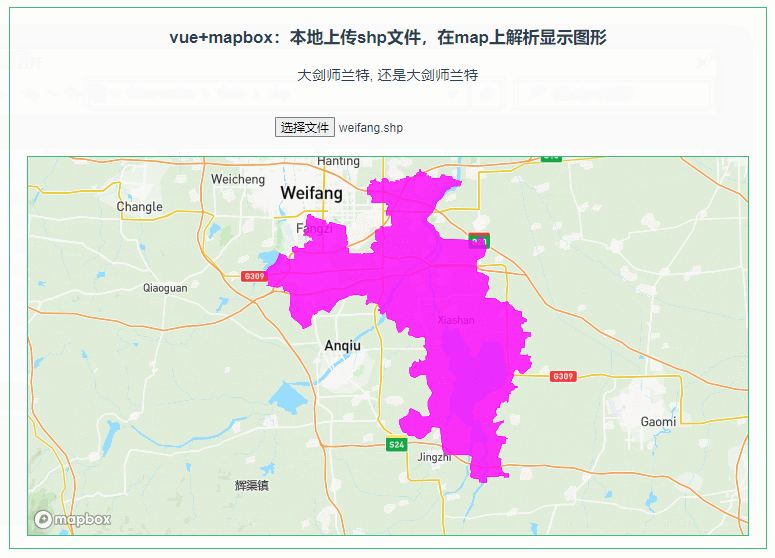
047:mapboxGL本地上传shp文件,在map上解析显示图形
第047个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+mapbox中本地上传shp文件,利用shapefile读取shp数据,并在地图上显示图形。 直接复制下面的 vue+mapbox源代码,操作2分钟即可运行实现效果 文章目录 示例效果配置方式示例源代码(共117行)加载shapefile.js方式…...
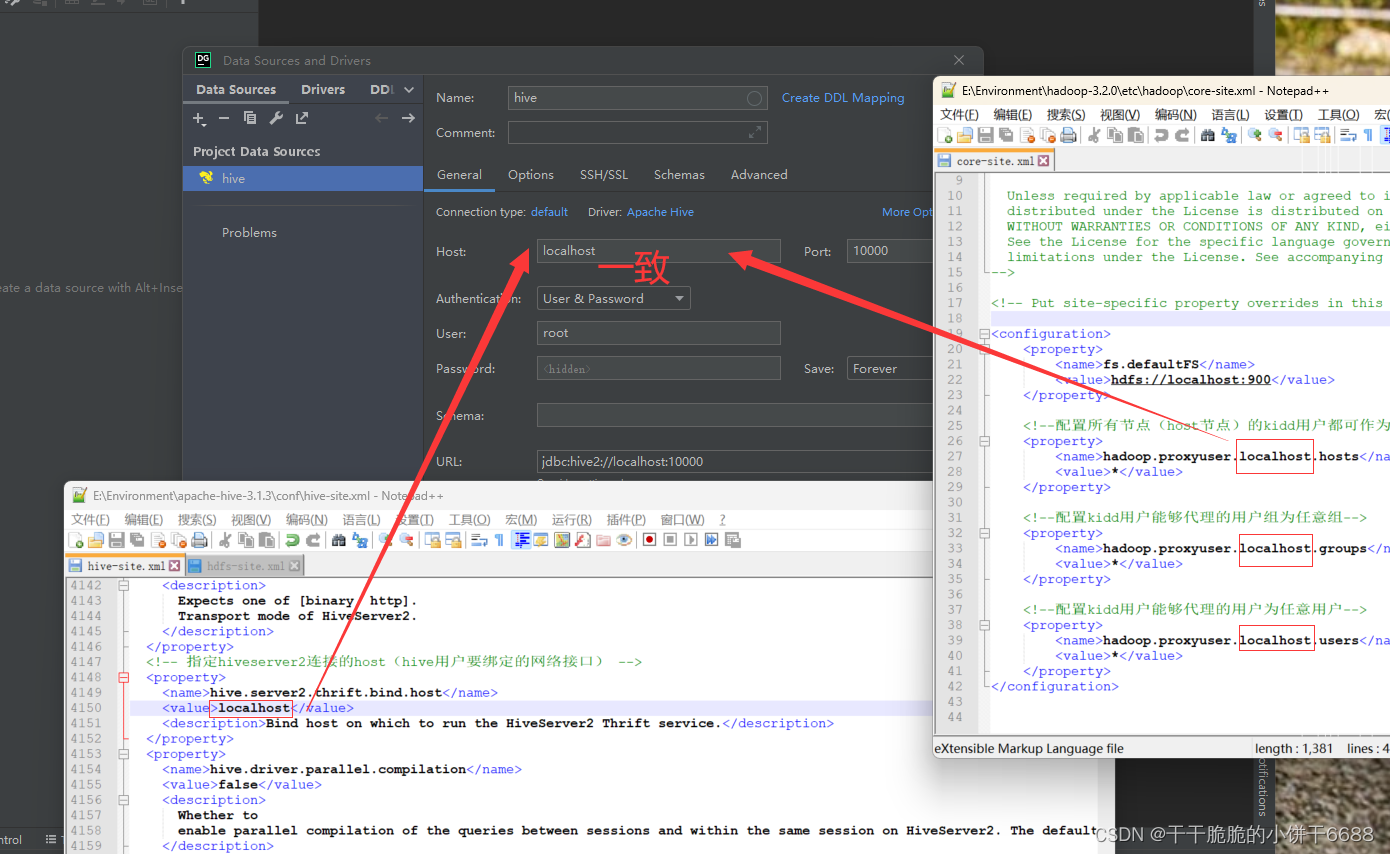
Windows下DataGrip连接Hive
DataGrip连接Hive 1. 启动Hadoop2. 启动hiveserver2服务3. 启动元数据服务4. 启动DG 1. 启动Hadoop 在控制台中输入start-all.cmd后,弹出下图4个终端(注意终端的名字)2. 启动hiveserver2服务 单独开一个窗口启动hiveserver2服务,…...
Xshell7和Xftp7超详细下载教程(包括安装及连接服务器附安装包)
1.下载 1.官网地址: XSHELL - NetSarang Website 选择学校免费版下载 2.将XSHELL和XFTP全都下载下来 2.安装 安装过程就是选择默认选项,然后无脑下一步 3.连接服务器 1.打开Xshell7,然后新建会话 2.填写相关信息 出现Connection establi…...

ASP.net数据从Controller传递到视图
最常见的方式是使用模型或 ViewBag。 使用模型传递数据: 在控制器中,创建一个模型对象,并将数据赋值给模型的属性。然后将模型传递给 View 方法。 public class HomeController : Controller {public IActionResult Index(){// 创建模型对…...

c++ 友元函数 友元类
1. 友元函数 1.1 简介 友元函数是在类的声明中声明的非成员函数,它被授予访问类的私有成员的权限。这意味着友元函数可以访问类的私有成员变量和私有成员函数,即使它们不是类的成员。 一个类中,可以将其他类或者函数声明为该类的友元&#…...

Spring推断构造器源码分析
Spring中bean虽然可以通过多种方式(Supplier接口、FactoryMethod、构造器)创建bean的实例对象,但是使用最多的还是通过构造器创建对象实例,也是我们最熟悉的创建对象的方式。如果有多个构造器时,那Spring是如何推断使用…...
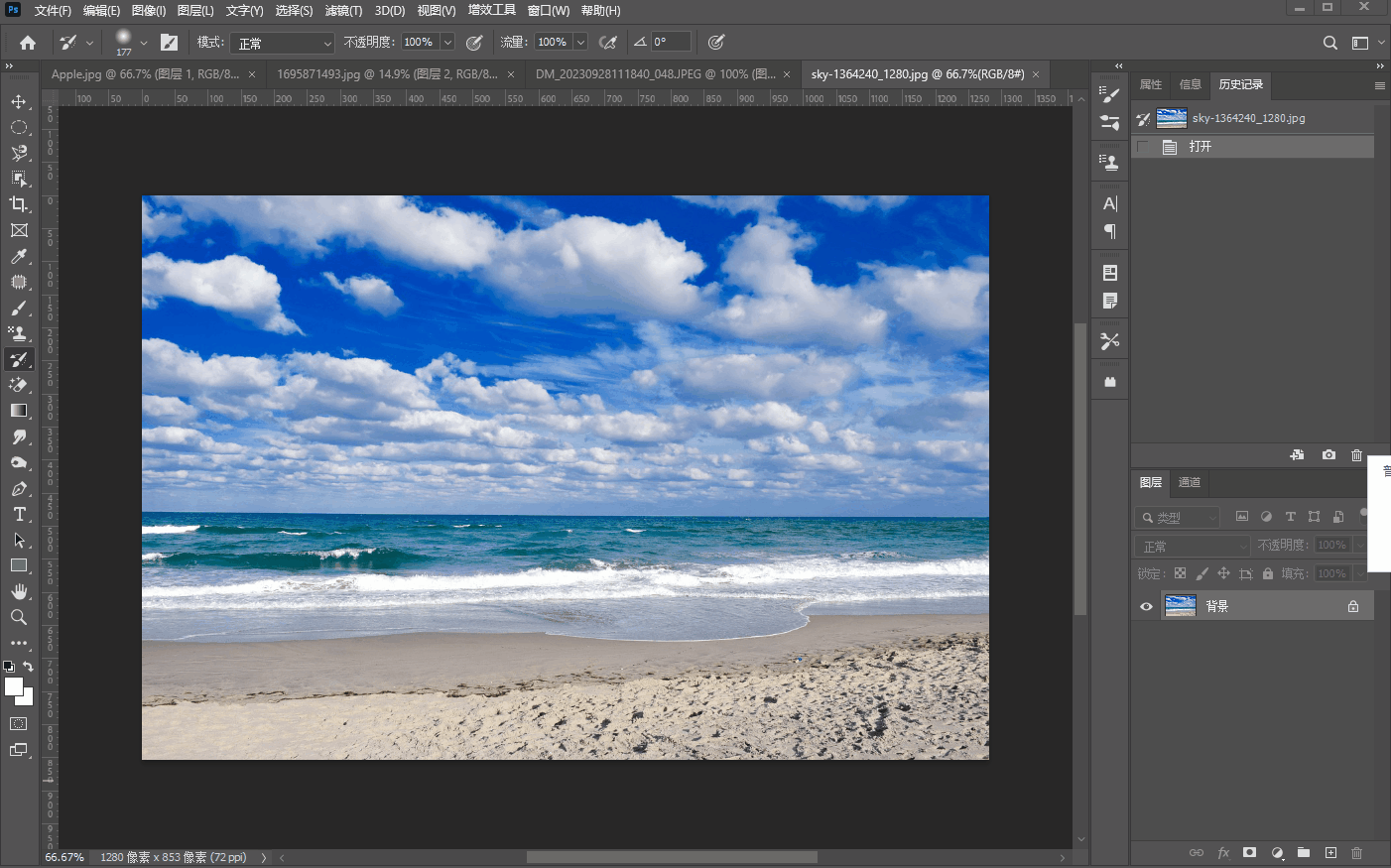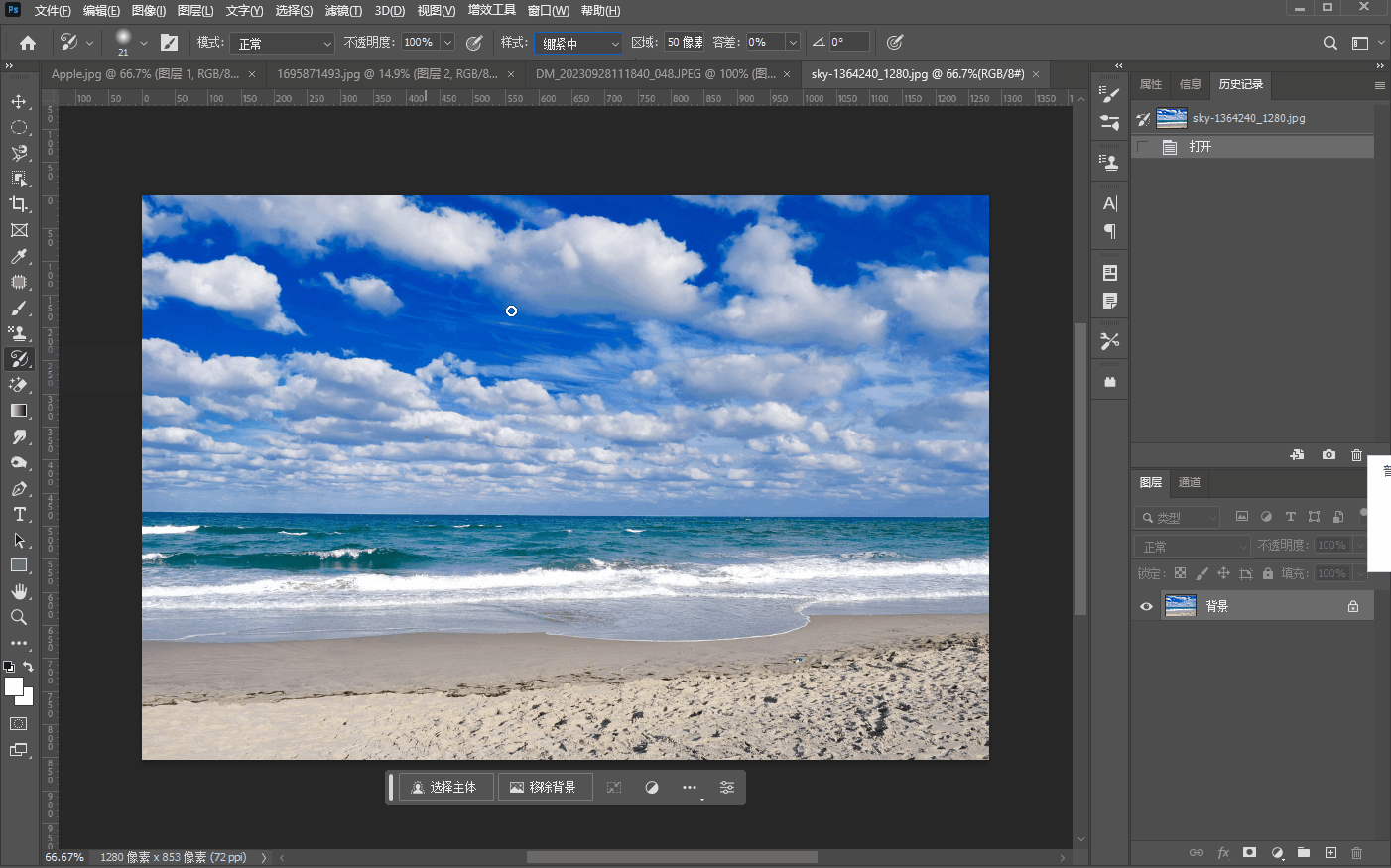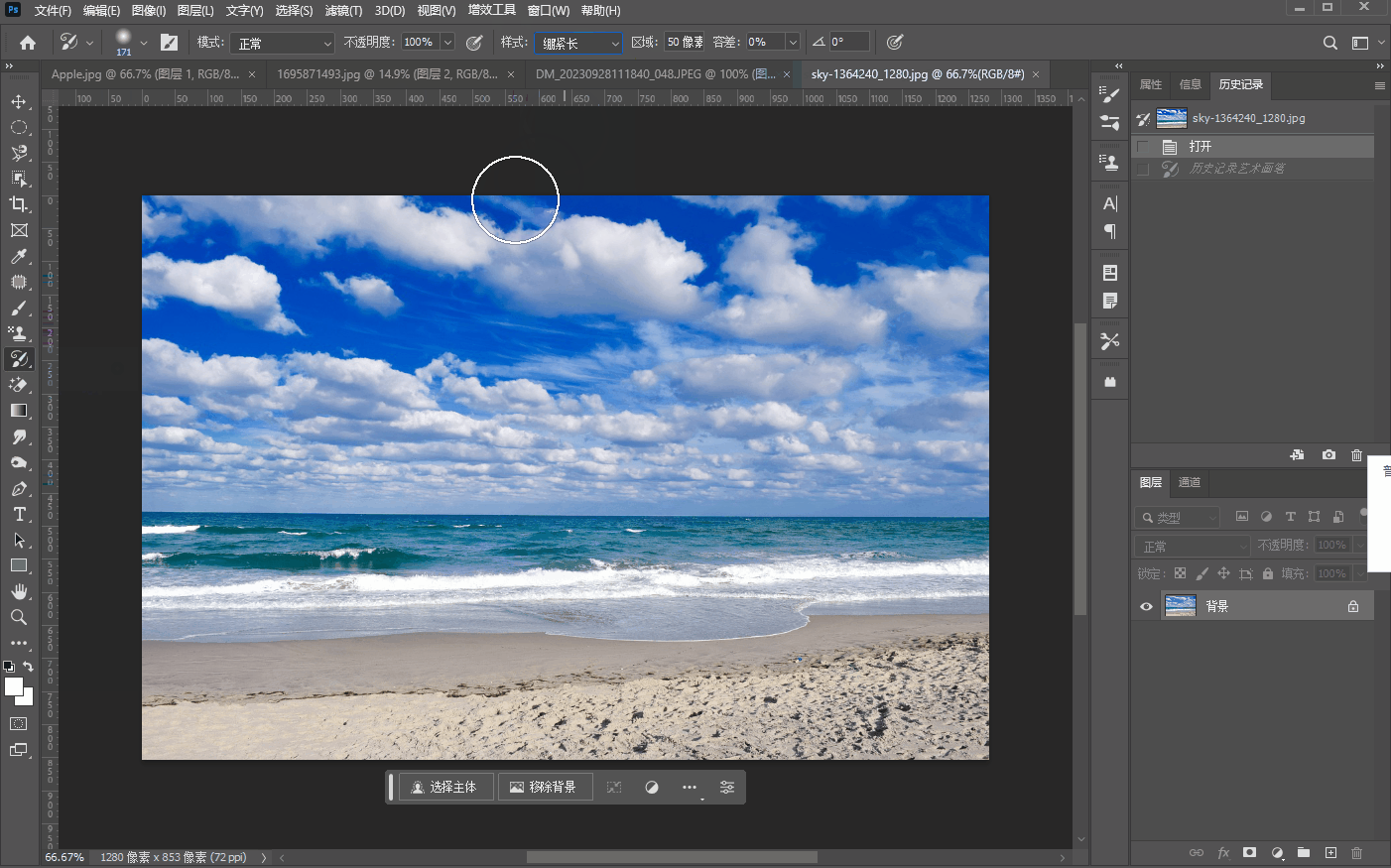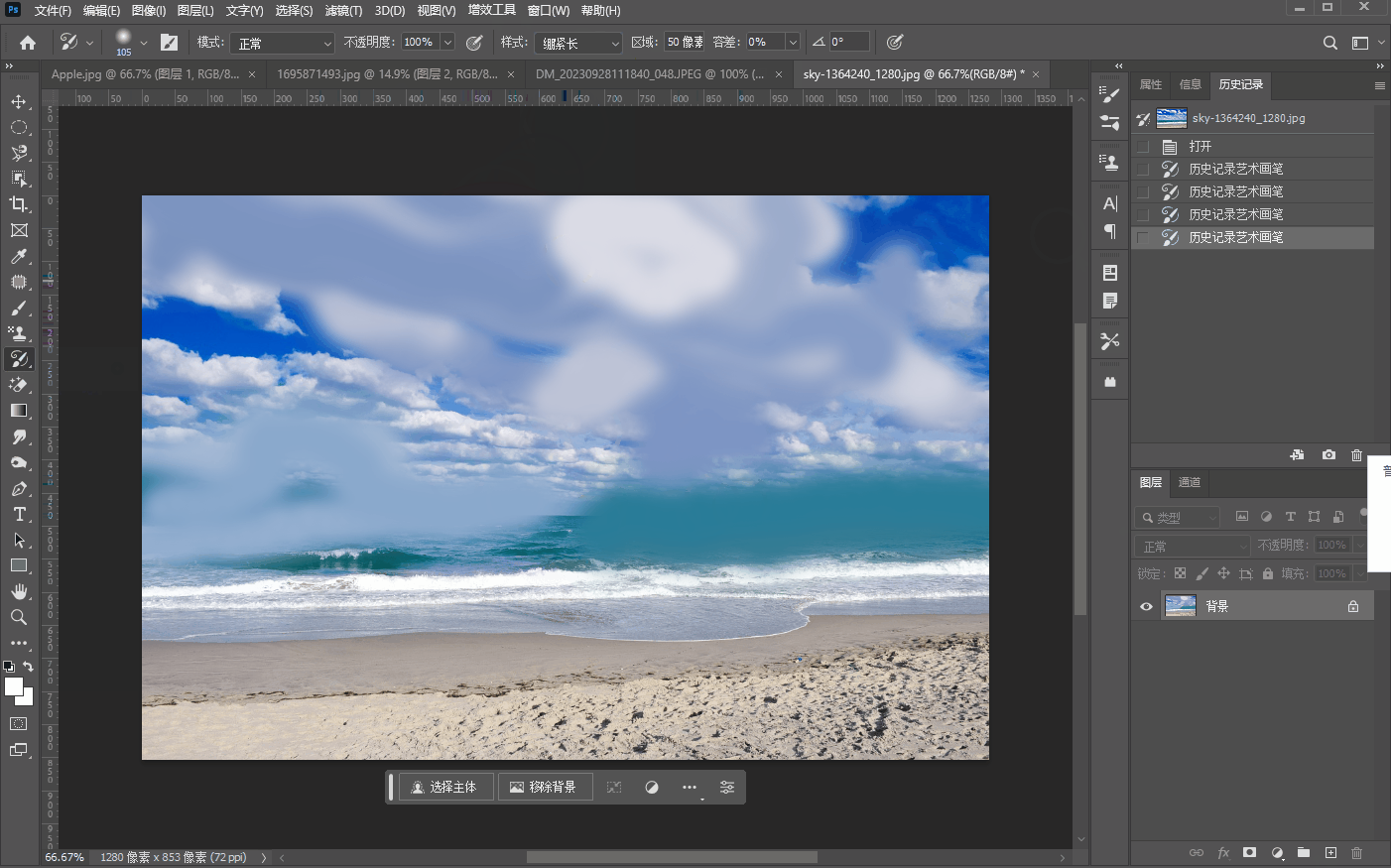
十五、【历史记录画笔工具组】
文章目录 历史记录画笔工具历史记录艺术画笔工具 历史记录画笔工具 历史记录画笔工具很简单,就是将画笔工具嗯,涂抹过的修改过的地方,然后用历史记录画笔工具重新修改回来,比如我们将三叠美元中的一叠用画笔工具先涂抹掉…...

Spark上使用pandas API快速入门
文章最前: 我是Octopus,这个名字来源于我的中文名--章鱼;我热爱编程、热爱算法、热爱开源。所有源码在我的个人github ;这博客是记录我学习的点点滴滴,如果您对 Python、Java、AI、算法有兴趣,可以关注我的…...
WEBRTC/StreamStatisticianImpl持续更新中))
【WebRTC---源码篇】(十:零)WEBRTC/StreamStatisticianImpl持续更新中)
StreamStatisticianImpl是WebRTC的一个内部实现类,用于统计和管理媒体流的各种统计信息。 StreamStatisticianImpl负责记录和计算以下统计数据: 1. 带宽统计:记录媒体流的发送和接收带宽信息,包括发送比特率、接收比特率、发送丢…...
报attempt to call a nil value (global ‘tostring‘)
调用Lua脚本tostring(xxx)报attempt to call a nil value (global ‘tostring‘
在c程序里调用Lua脚本, 脚本中用到了转字符串 tostring(xxx) str "test" function output(a,b,c)d "a:"..tostring(a).."b:"..tostring(b).."c"..tostring(c)return d end 实际运行会报错: attempt to call a nil v…...
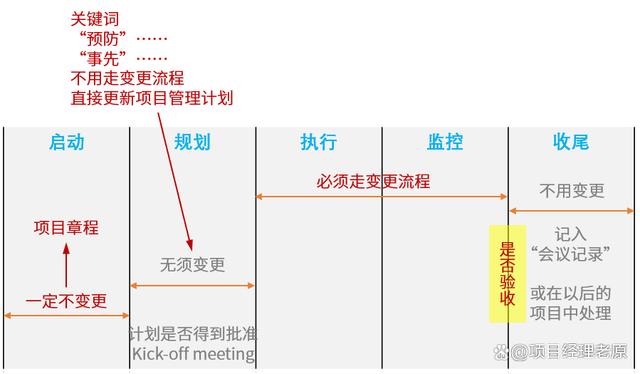
PBA.客户需求分析 需求管理
一、客户需求分析 1 需求的三个层次: Requirement/Wants/Pains 大部分人认为,产品满足不了客户需要,是因为客户告知的需求是错误的,这听起来有一些道理,却没有任何意义。不同角色对于需求的理解是不一样的。在客户的需求和厂家的…...
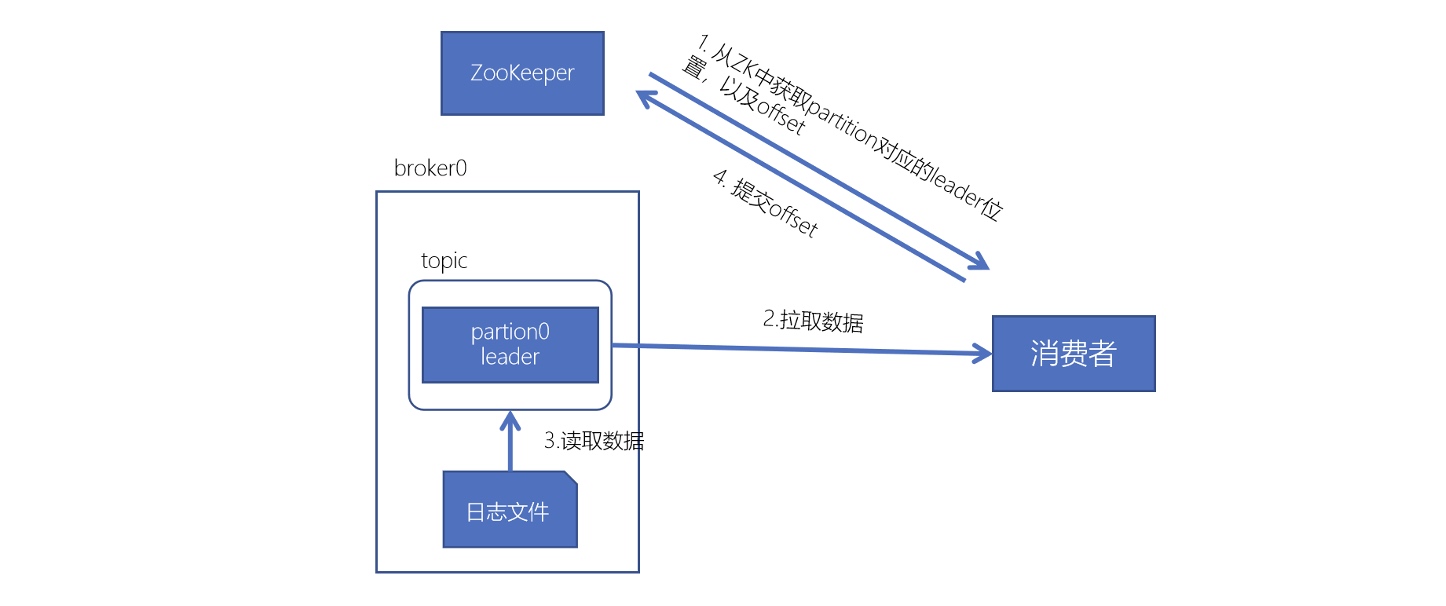
Kafka进阶
Kafka进阶 Kafka事务 kafka的事务机制是指kafka支持跨多个主题和分区的原子性写入,即在一个事务中发送的所有消息要么全部成功,要么全部失败。 kafka的事务机制涉及到以下几个方面: 事务生产者(transactional producer&#x…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
