《论文阅读:Dataset Condensation with Distribution Matching》
点进去这篇文章的开源地址,才发现这篇文章和DC DSA居然是一个作者,数据浓缩写了三篇论文,第一篇梯度匹配,第二篇数据增强后梯度匹配,第三篇匹配数据分布。DC是匹配浓缩数据和原始数据训练一次后的梯度差,DSA是在DC前加入了一层数据增强,DM直接就匹配浓缩数据和原始数据丢入模型得到的输出,匹配输出的分布。
一个github地址包含了三个数据浓缩方法的开源代码。
1. 基于分布匹配的数据集浓缩
在降低训练成本方面,最近一个很有前途的方向是数据集凝聚,其目的是在保留原始信息的情况下,用一个小得多的学习合成集取代原来的大训练集。
虽然在小集合的压缩图像上训练深度模型可以非常快,但由于复杂的双层优化和二阶导数计算,它们的合成仍然是计算昂贵的(DD,DC,DSA)。
在本工作中,我们提出了一种简单而有效的方法,通过匹配合成图像和原始训练图像在多个采样嵌入空间的特征分布来合成压缩图像。我们的方法显著降低了合成成本,同时实现了相当或更好的性能。
2. 方法
2.1 数据浓缩的问题:
现有的方法包括DD,DC和DSA等,他们的弊端在于时间复杂度太高,内层需要训练模型并更新浓缩数据集,外层还需要适应不同的 θ 0 \theta_0 θ0,实现起来需要三层循环,时间复杂度高。
2.2 分布匹配的数据浓缩
真实数据分布记为 P D P_{\mathcal{D}} PD。
我们将训练数据记为 x ∈ ℜ d \boldsymbol{x} \in \Re^d x∈ℜd ,并且可以被编码到一个低维空间,通过函数 ψ ϑ : ℜ d → ℜ d ′ \psi_{\vartheta}: \Re^d \rightarrow \Re^{d^{\prime}} ψϑ:ℜd→ℜd′ ,其中 d ′ ≪ d d^{\prime} \ll d d′≪d , ϑ \vartheta ϑ 是函数的参数数值。 换句话说,每个embedding 函数 ψ \psi ψ可以被视为提供其输入的部分解释,而它们的组合则提供完整的解释。
现在我们可以使用常用的最大平均差异(MMD)来估计真实数据分布和合成数据分布之间的距离:
sup ∥ ψ ϑ ∥ H ≤ 1 ( E [ ψ ϑ ( T ) ] − E [ ψ ϑ ( S ) ] ) \sup _{\left\|\psi_{\vartheta}\right\|_{\mathcal{H}} \leq 1}\left(\mathbb{E}\left[\psi_{\vartheta}(\mathcal{T})\right]-\mathbb{E}\left[\psi_{\vartheta}(\mathcal{S})\right]\right) ∥ψϑ∥H≤1sup(E[ψϑ(T)]−E[ψϑ(S)])
由于我们无法获得真实数据分布,因此我们使用 MMD 的经验估计:
E ϑ ∼ P ϑ ∥ 1 ∣ T ∣ ∑ i = 1 ∣ T ∣ ψ ϑ ( x i ) − 1 ∣ S ∣ ∑ j = 1 ∣ S ∣ ψ ϑ ( s j ) ∥ 2 \mathbb{E}_{\boldsymbol{\vartheta} \sim P_{\vartheta}}\left\|\frac{1}{|\mathcal{T}|} \sum_{i=1}^{|\mathcal{T}|} \psi_{\boldsymbol{\vartheta}}\left(\boldsymbol{x}_i\right)-\frac{1}{|\mathcal{S}|} \sum_{j=1}^{|\mathcal{S}|} \psi_{\boldsymbol{\vartheta}}\left(\boldsymbol{s}_j\right)\right\|^2 Eϑ∼Pϑ ∣T∣1i=1∑∣T∣ψϑ(xi)−∣S∣1j=1∑∣S∣ψϑ(sj) 2
就是在不同参数取值的embedding函数下,输入原始数据和浓缩数据得到的输出要尽可能接近,论文里就直接使用了神经网络的输出,让神经网络的输出尽可能接近。
因为这篇论文是DSA的后续作,所以顺其自然,沿用了DSA的方法,训练的时候对浓缩数据和原始数据都进行了相同的数据增强。
min S E ω ∼ P ϑ ω ∼ Ω ∥ 1 ∣ T ∣ ∑ i = 1 ∣ T ∣ ψ ϑ ( A ( x i , ω ) ) − 1 ∣ S ∣ ∑ j = 1 ∣ S ∣ ψ ϑ ( A ( s j , ω ) ) ∥ 2 \min _{\mathcal{S}} \mathbb{E}_{\substack{\boldsymbol{\omega} \sim P_{\boldsymbol{\vartheta}} \\ \omega \sim \Omega}}\left\|\frac{1}{|\mathcal{T}|} \sum_{i=1}^{|\mathcal{T}|} \psi_{\boldsymbol{\vartheta}}\left(\mathcal{A}\left(\boldsymbol{x}_i, \omega\right)\right)-\frac{1}{|\mathcal{S}|} \sum_{j=1}^{|\mathcal{S}|} \psi_{\boldsymbol{\vartheta}}\left(\mathcal{A}\left(\boldsymbol{s}_j, \omega\right)\right)\right\|^2 SminEω∼Pϑω∼Ω ∣T∣1i=1∑∣T∣ψϑ(A(xi,ω))−∣S∣1j=1∑∣S∣ψϑ(A(sj,ω)) 2
A \mathcal{A} A就是对应的数据增强操作, ω \omega ω是对应数据增强操作的参数。
2.3 训练步骤

训练K-1步,每一步都选定一个embedding函数的参数,不断地训练并修改S使得S输出尽可能接近原始数据集T。(这个embedding函数就是一个具体的神经网络)
3. 结果
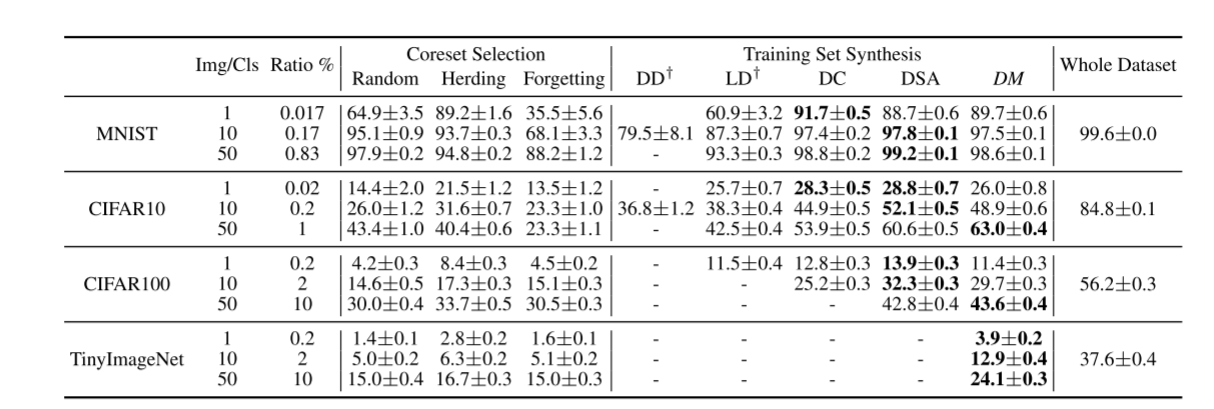
由于此方法计算不需要计算梯度,只需要正向传播embedding网络,得到输出之后反向传播浓缩数据集S即可,因此可以压缩到更多数量的图片上,并且第一次在TinyImageNet这种大数据集上进行压缩。
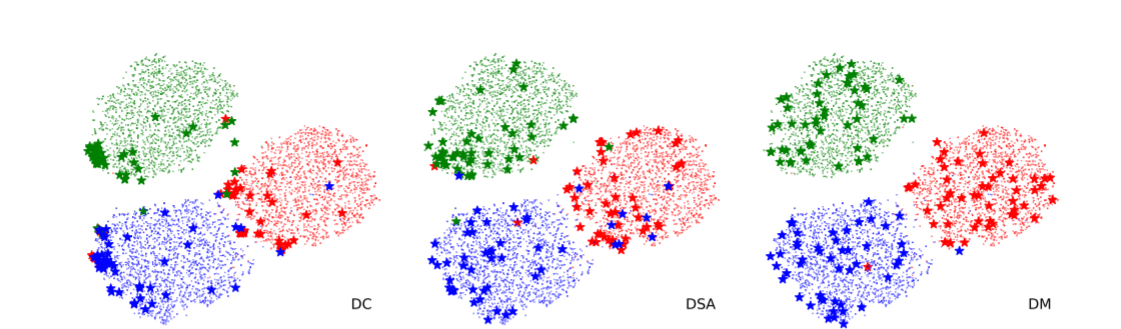
比起DC和DSA,DM得到的数据分布更接近原始数据分布。
相关文章:

《论文阅读:Dataset Condensation with Distribution Matching》
点进去这篇文章的开源地址,才发现这篇文章和DC DSA居然是一个作者,数据浓缩写了三篇论文,第一篇梯度匹配,第二篇数据增强后梯度匹配,第三篇匹配数据分布。DC是匹配浓缩数据和原始数据训练一次后的梯度差,DS…...
免费chatGPT工具
发现很多人还是找不到好用的chatGPT工具,这里分享一个邮箱注册即可免费试用。 PromptsZone - 一体化人工智能平台使用 PromptsZone 与 ChatGPT、Claude、AI21 Labs、Google Bard 聊天,并使用 DALL-E、Stable Diffusion 和 Google Imagegen 创建图像&…...

数据分析基础:数据可视化+数据分析报告
数据分析是指通过对大量数据进行收集、整理、处理和分析,以发现其中的模式、趋势和关联,并从中提取有价值的信息和知识。 数据可视化和数据分析报告是数据分析过程中非常重要的两个环节,它们帮助将数据转化为易于理解和传达的形式࿰…...

settings.xml的文件配置大全
settings.xml 文件中最常配置的还是这几个标签 localRepository和mirrors settings.xml文件官方文档地址 <settings xmlns"http://maven.apache.org/SETTINGS/1.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"ht…...
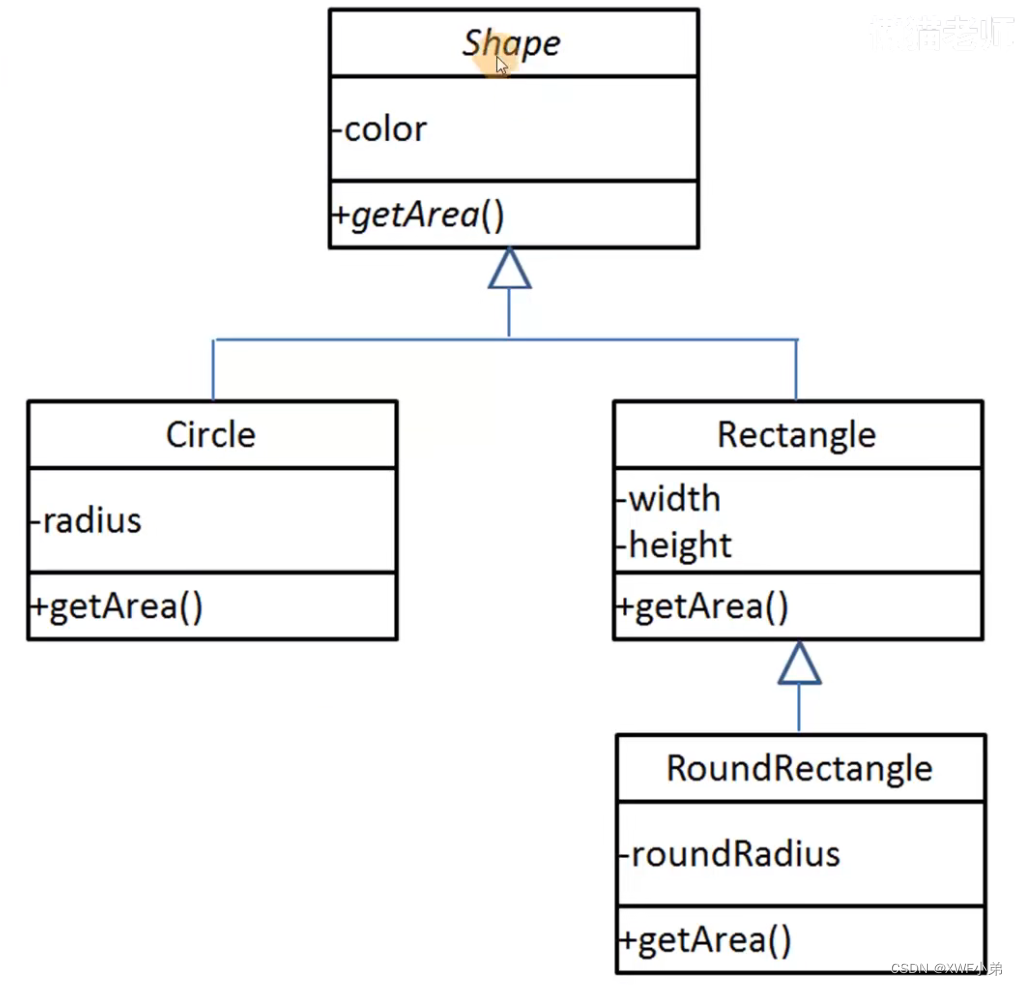
极简c++(7)类的继承
为什么要用继承 子类不必复制父类的任何属性,已经继承下来了;易于维护与编写; 类的继承与派生 访问控制规则 一般只使用Public! 构造函数的继承与析构函数的继承 构造函数不被继承! 在创建子类对象的时候&…...
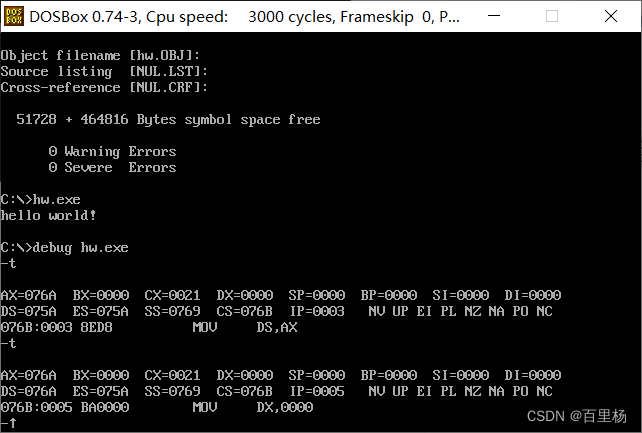
DOSBox和MASM汇编开发环境搭建
DOSBox和MASM汇编开发环境搭建 1 安装DOSBox2 安装MASM3 编译测试代码4 运行测试代码5 调试测试代码 本文属于《 X86指令基础系列教程》之一,欢迎查看其它文章。 1 安装DOSBox 下载DOSBox和MASM:https://download.csdn.net/download/u011832525/884180…...
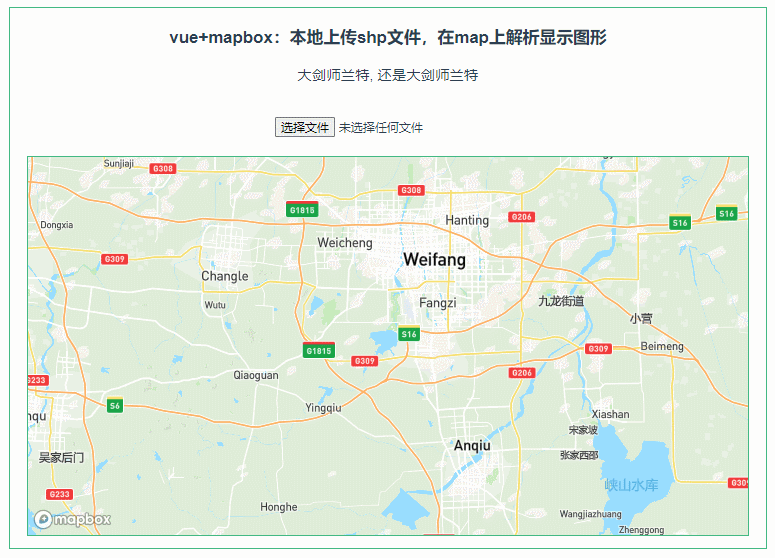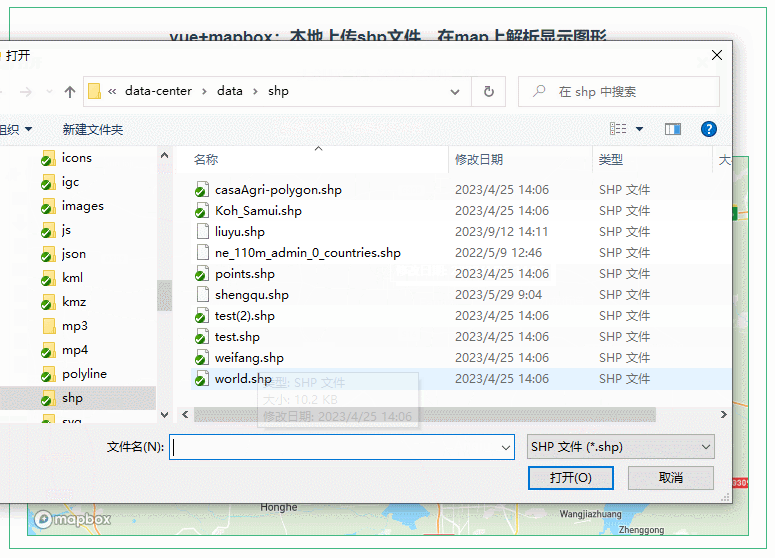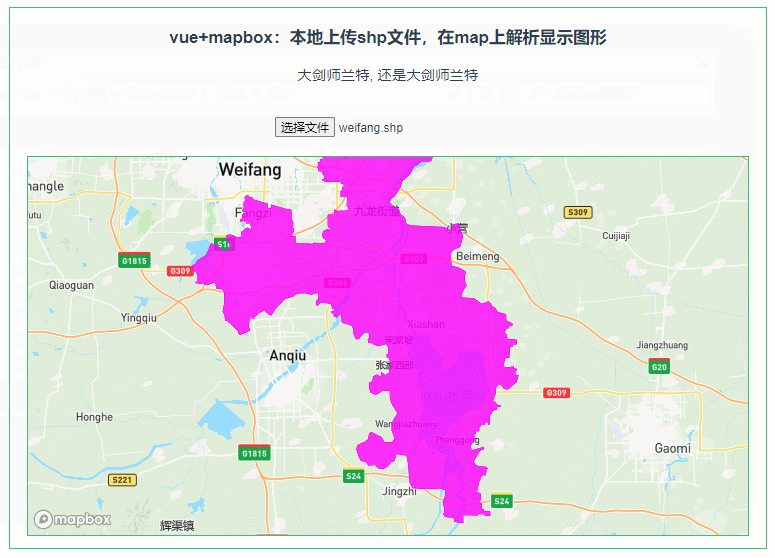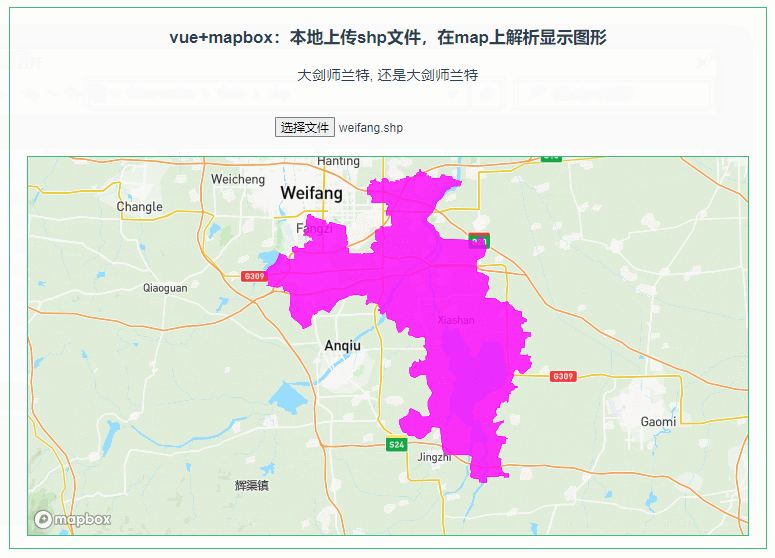
047:mapboxGL本地上传shp文件,在map上解析显示图形
第047个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+mapbox中本地上传shp文件,利用shapefile读取shp数据,并在地图上显示图形。 直接复制下面的 vue+mapbox源代码,操作2分钟即可运行实现效果 文章目录 示例效果配置方式示例源代码(共117行)加载shapefile.js方式…...
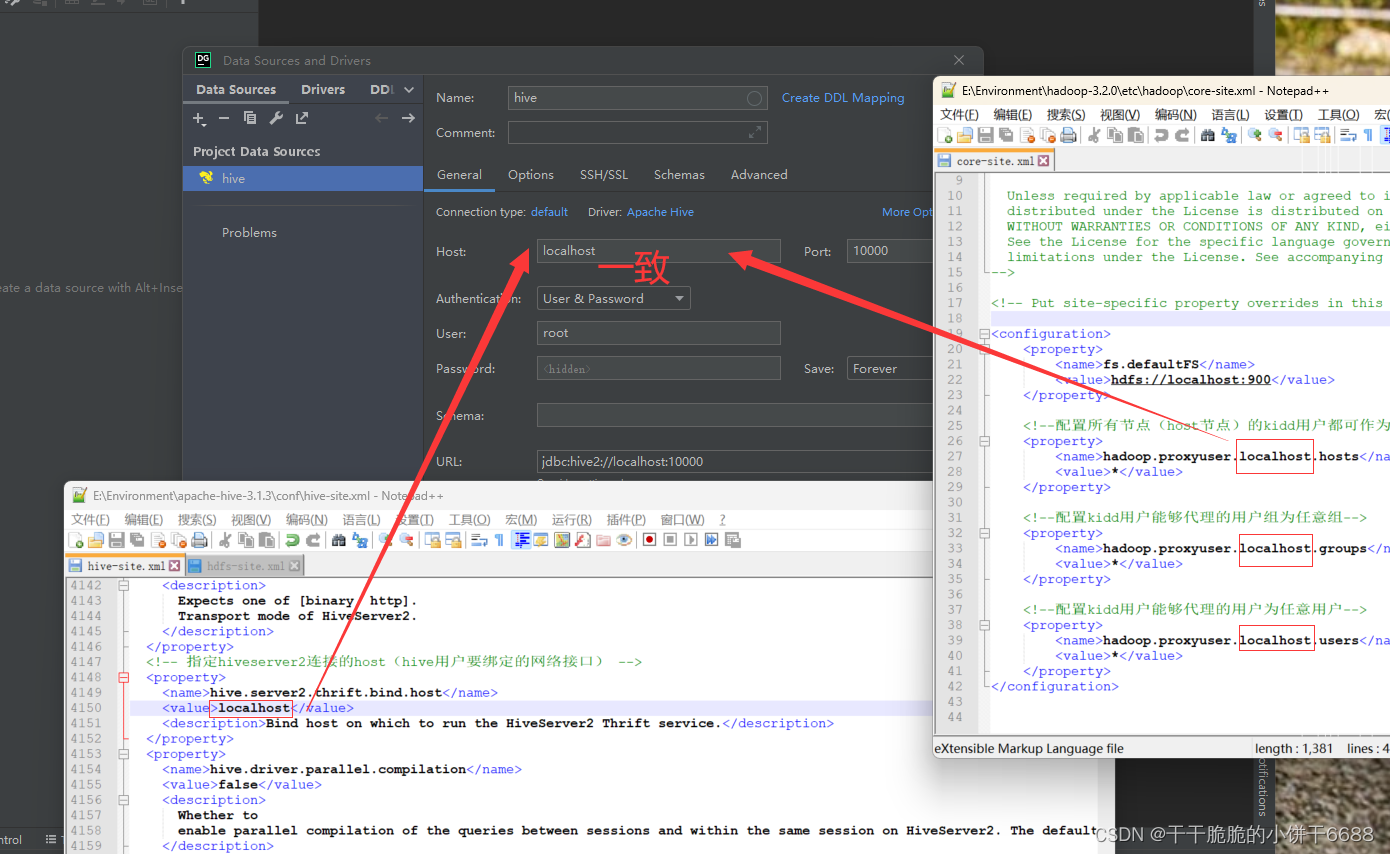
Windows下DataGrip连接Hive
DataGrip连接Hive 1. 启动Hadoop2. 启动hiveserver2服务3. 启动元数据服务4. 启动DG 1. 启动Hadoop 在控制台中输入start-all.cmd后,弹出下图4个终端(注意终端的名字)2. 启动hiveserver2服务 单独开一个窗口启动hiveserver2服务,…...
Xshell7和Xftp7超详细下载教程(包括安装及连接服务器附安装包)
1.下载 1.官网地址: XSHELL - NetSarang Website 选择学校免费版下载 2.将XSHELL和XFTP全都下载下来 2.安装 安装过程就是选择默认选项,然后无脑下一步 3.连接服务器 1.打开Xshell7,然后新建会话 2.填写相关信息 出现Connection establi…...

ASP.net数据从Controller传递到视图
最常见的方式是使用模型或 ViewBag。 使用模型传递数据: 在控制器中,创建一个模型对象,并将数据赋值给模型的属性。然后将模型传递给 View 方法。 public class HomeController : Controller {public IActionResult Index(){// 创建模型对…...

c++ 友元函数 友元类
1. 友元函数 1.1 简介 友元函数是在类的声明中声明的非成员函数,它被授予访问类的私有成员的权限。这意味着友元函数可以访问类的私有成员变量和私有成员函数,即使它们不是类的成员。 一个类中,可以将其他类或者函数声明为该类的友元&#…...

Spring推断构造器源码分析
Spring中bean虽然可以通过多种方式(Supplier接口、FactoryMethod、构造器)创建bean的实例对象,但是使用最多的还是通过构造器创建对象实例,也是我们最熟悉的创建对象的方式。如果有多个构造器时,那Spring是如何推断使用…...
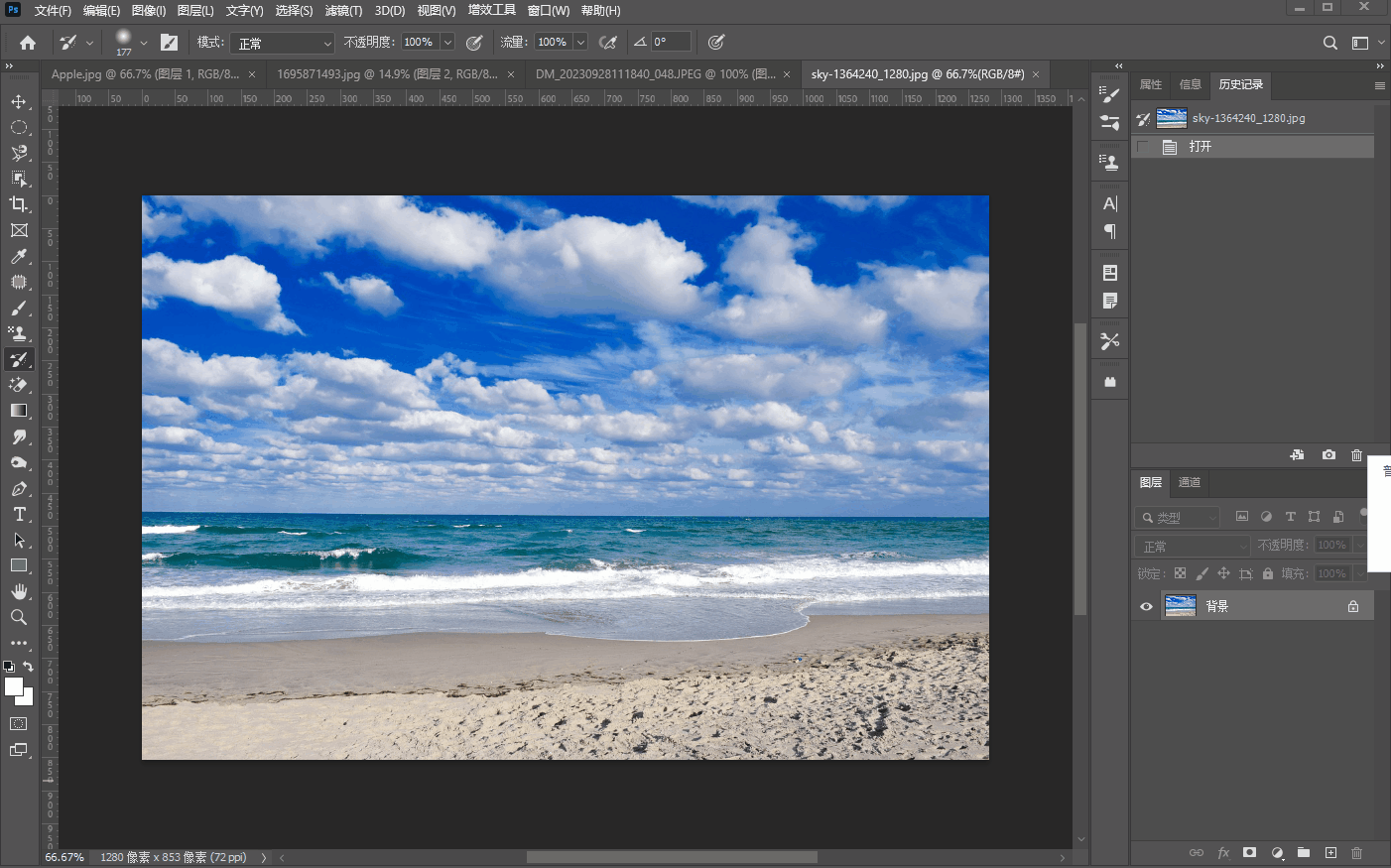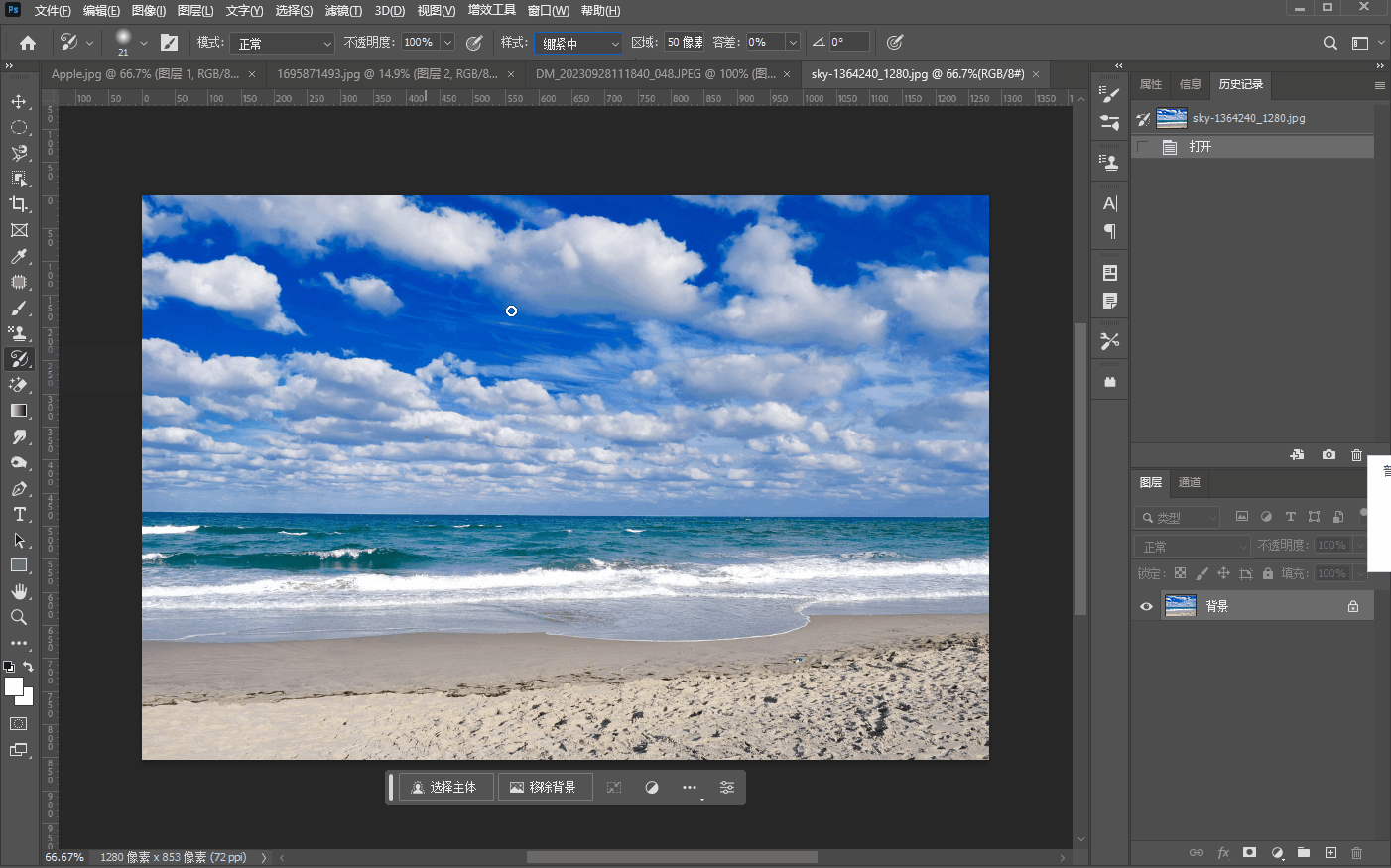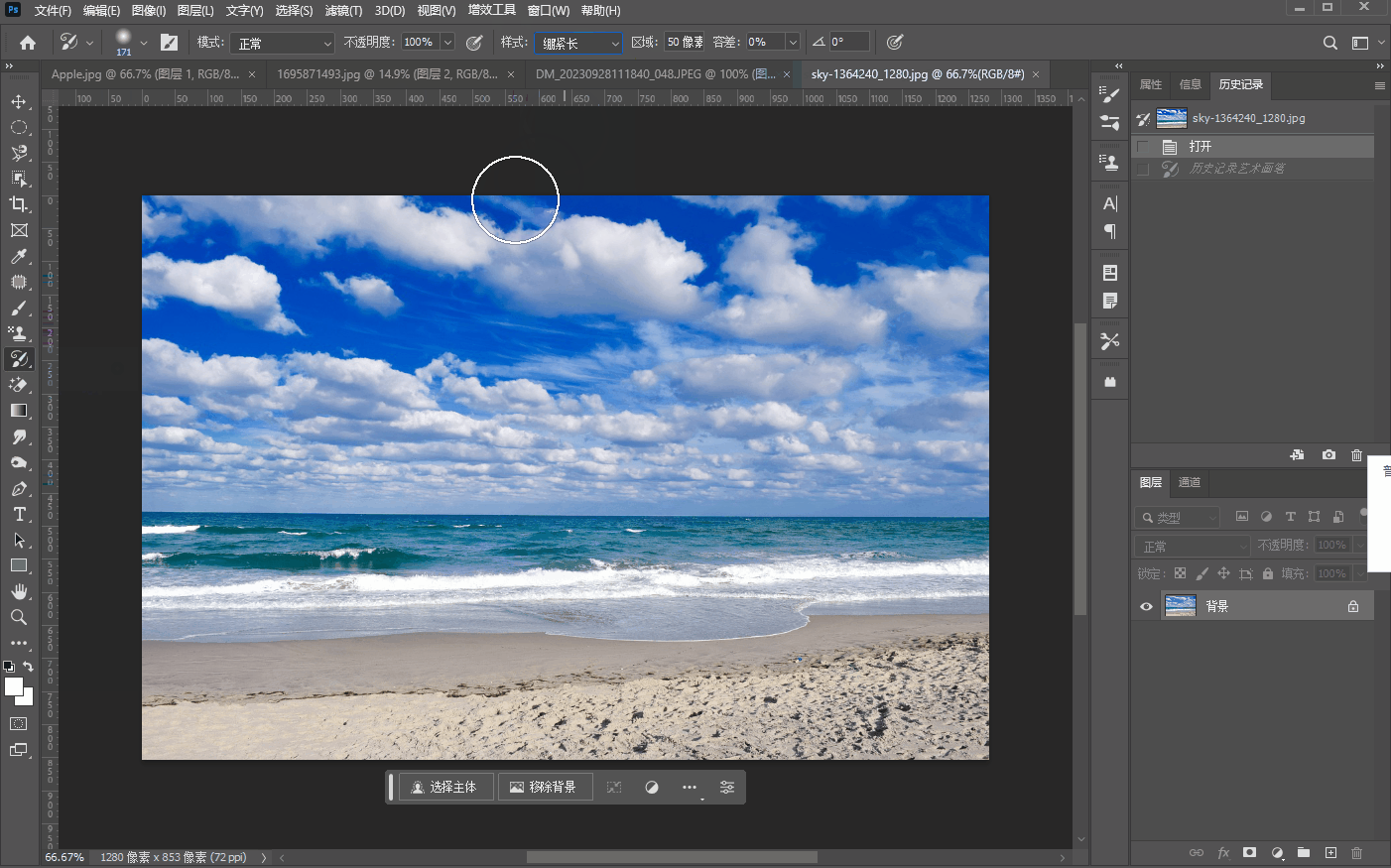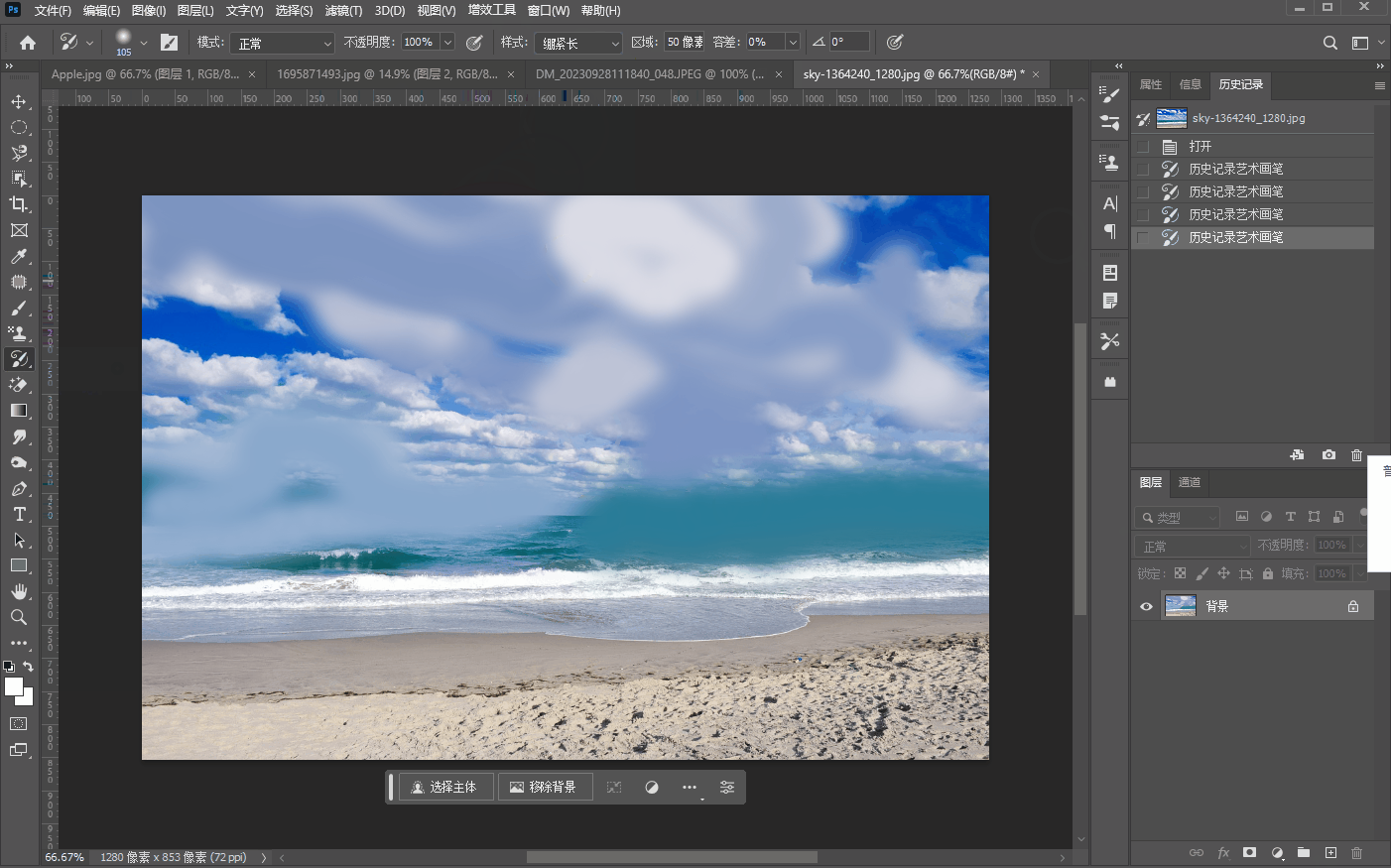
十五、【历史记录画笔工具组】
文章目录 历史记录画笔工具历史记录艺术画笔工具 历史记录画笔工具 历史记录画笔工具很简单,就是将画笔工具嗯,涂抹过的修改过的地方,然后用历史记录画笔工具重新修改回来,比如我们将三叠美元中的一叠用画笔工具先涂抹掉…...

Spark上使用pandas API快速入门
文章最前: 我是Octopus,这个名字来源于我的中文名--章鱼;我热爱编程、热爱算法、热爱开源。所有源码在我的个人github ;这博客是记录我学习的点点滴滴,如果您对 Python、Java、AI、算法有兴趣,可以关注我的…...
WEBRTC/StreamStatisticianImpl持续更新中))
【WebRTC---源码篇】(十:零)WEBRTC/StreamStatisticianImpl持续更新中)
StreamStatisticianImpl是WebRTC的一个内部实现类,用于统计和管理媒体流的各种统计信息。 StreamStatisticianImpl负责记录和计算以下统计数据: 1. 带宽统计:记录媒体流的发送和接收带宽信息,包括发送比特率、接收比特率、发送丢…...
报attempt to call a nil value (global ‘tostring‘)
调用Lua脚本tostring(xxx)报attempt to call a nil value (global ‘tostring‘
在c程序里调用Lua脚本, 脚本中用到了转字符串 tostring(xxx) str "test" function output(a,b,c)d "a:"..tostring(a).."b:"..tostring(b).."c"..tostring(c)return d end 实际运行会报错: attempt to call a nil v…...
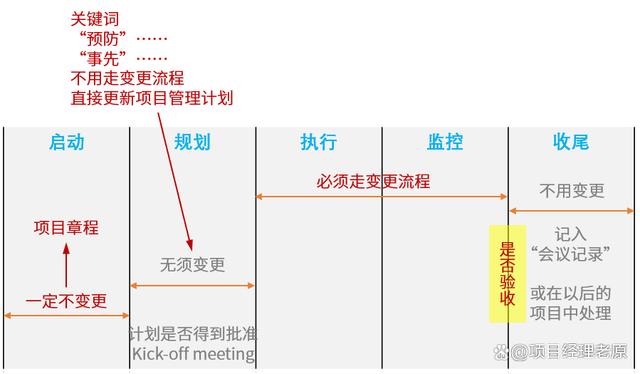
PBA.客户需求分析 需求管理
一、客户需求分析 1 需求的三个层次: Requirement/Wants/Pains 大部分人认为,产品满足不了客户需要,是因为客户告知的需求是错误的,这听起来有一些道理,却没有任何意义。不同角色对于需求的理解是不一样的。在客户的需求和厂家的…...
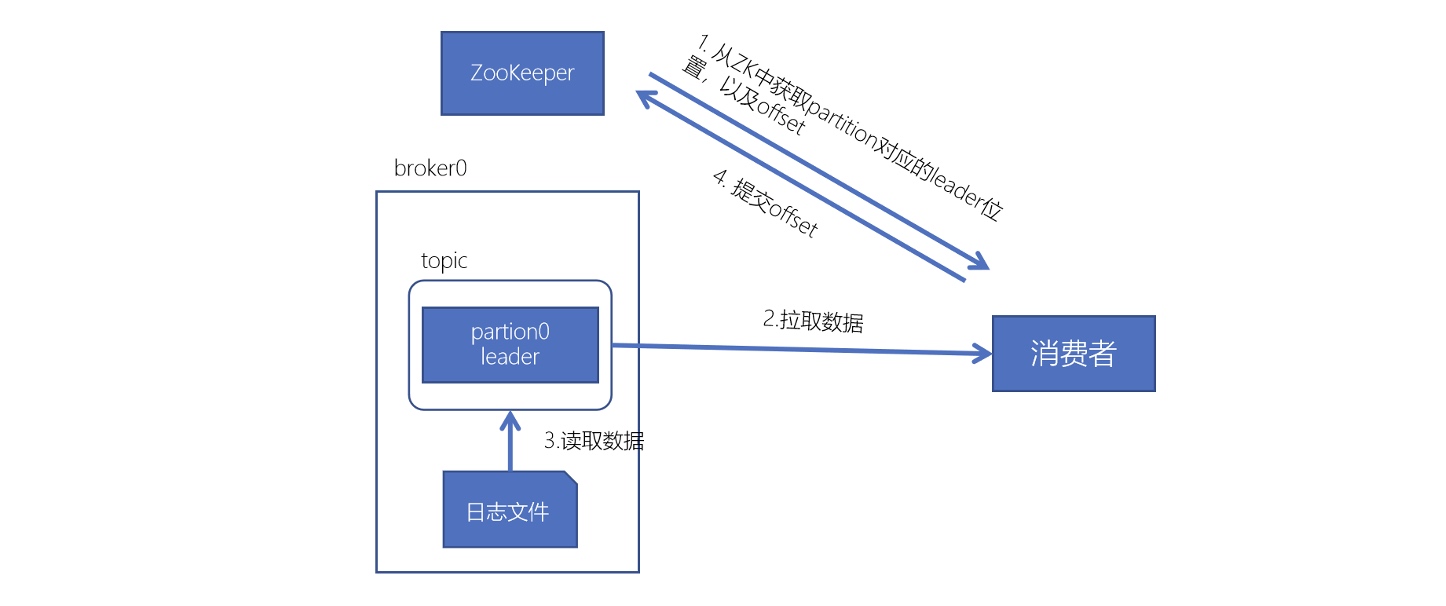
Kafka进阶
Kafka进阶 Kafka事务 kafka的事务机制是指kafka支持跨多个主题和分区的原子性写入,即在一个事务中发送的所有消息要么全部成功,要么全部失败。 kafka的事务机制涉及到以下几个方面: 事务生产者(transactional producer&#x…...
大数计算:e^1000/300!
1.问题:大数计算可能超出数据类型范围 当单独计算 ,因为 ,double的最大取值为1.79769e308,所以 肯定超过了double的表示范围。 同样,对于300!也是如此。 那我们应该怎么去计算和存储结果呢?…...
力扣164最大间距
1.前言 因为昨天写了一个基数排序,今天我来写一道用基数排序实现的题解,希望可以帮助你理解基数排序。 这个题本身不难,就是线性时间和线性额外空间(O(n))的算法,有点难实现 基数排序的时间复杂度是O(d*(nradix)),其中…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
