大数计算:e^1000/300!
1.问题:大数计算可能超出数据类型范围
当单独计算 ,因为
,double的最大取值为1.79769e+308,所以
肯定超过了double的表示范围。
同样,对于300!也是如此。
那我们应该怎么去计算和存储结果呢?
2.解决方案
从数学角度出发,对于超级大的数,运算方式、运算规律等肯定保持不变的。
很多时候,我们主要是利用相关的定理、公式进行简化或者极限处理。
由于我项目里的精度要求就 e-10,于是,可以采用相对宽松的方式解决这个问题:
科学计数法!
3.代码实现
#ifndef __BigNumeric_h
#define __BigNumeric_h
#include <cmath>template<typename _T>
class BigNumeric
{
private:_T mantissa; //基数int exponent; //指数public:BigNumeric(_T num){if (num == 0) {exponent = 0;mantissa = 0;}else{exponent = std::floor(std::log10(std::abs(num)));mantissa = num / std::pow(10, exponent);}}~BigNumeric(){}BigNumeric(const BigNumeric& other){if (this == &other) return;this->exponent = other.exponent;this->mantissa = other.mantissa;}BigNumeric& operator=(const BigNumeric& other){/*if(this == &other) return *this;*/this->exponent = other.exponent;this->mantissa = other.mantissa;return *this;}public:_T value(){if (this->exponent >= 308) return 0.0;return this->mantissa * std::pow(10.0, this->exponent);}//乘法BigNumeric& operator*(const BigNumeric& opr){BigNumeric<_T> resmnt(this->mantissa * opr.mantissa);this->exponent = resmnt.exponent + this->exponent + opr.exponent;this->mantissa = resmnt.mantissa;return *this;}BigNumeric& operator*(const _T opr){BigNumeric<_T> oprbgn(opr);*this = *this * oprbgn;return *this;}friend BigNumeric operator*(const _T opr1, BigNumeric& opr2){return opr2 * opr1;}//除法BigNumeric& operator/(const BigNumeric& opr){BigNumeric<_T> resmnt(this->mantissa / opr.mantissa);this->exponent = resmnt.exponent + this->exponent - opr.exponent;this->mantissa = resmnt.mantissa;return *this;}BigNumeric& operator/(const _T opr){BigNumeric<_T> oprbgn(opr);*this = *this / oprbgn;return *this;}friend BigNumeric operator/(const _T opr, const BigNumeric& opr1){BigNumeric<_T> oprbgn(opr);return oprbgn / opr1;}//加法BigNumeric& operator+(const BigNumeric& opr){if (this->exponent - opr.exponent > 15) return *this;else if (this->exponent - opr.exponent < -15){*this = opr;return *this;} int min = this->exponent > opr.exponent ? opr.exponent : this->exponent;BigNumeric<_T> resmnt(this->mantissa * std::pow(10.0, this->exponent - min) + opr.mantissa * std::pow(10.0, opr.exponent - min));this->exponent = resmnt.exponent + min;this->mantissa = resmnt.mantissa;return *this;}BigNumeric& operator+(const _T opr){BigNumeric<_T> oprbgn(opr);*this = *this + oprbgn;return *this;}friend BigNumeric operator+(const _T opr1, BigNumeric& opr2){return opr2 + opr1;}//减法BigNumeric& operator-(const BigNumeric& opr){BigNumeric temp(opr);*this = *this + temp * (-1.0);return *this;}BigNumeric& operator-(const _T opr){BigNumeric oprbgn(opr);*this = *this - oprbgn;return *this;}friend BigNumeric operator-(const _T opr1, BigNumeric& opr2){return opr2 - opr1;}//开方BigNumeric& Sqrt(){_T bgnmant = std::sqrt(this->mantissa);int bgnexp = this->exponent;if (bgnexp % 2 == 0){this->mantissa = bgnmant;this->exponent = bgnexp / 2;}else{BigNumeric temp(bgnmant * std::sqrt(10.0));this->mantissa = temp.mantissa;this->exponent = temp.exponent + bgnexp / 2;}return *this;}//幂BigNumeric& Pow(_T exp){BigNumeric temp(Vpow(this->mantissa, exp));this->mantissa = temp.mantissa;this->exponent = temp.exponent + this->exponent * exp;return *this;}public:static BigNumeric Factorial(int opr){if (opr < 0) return 1.0 / Factorial(-1.0 * opr + 1);else if (opr == 0) return BigNumeric(1.0);return Factorial(opr - 1) * opr;}static BigNumeric Epow(_T exp){BigNumeric res(1.0);double e = 2.71828182845904523536;if (std::abs(exp) <= 700) return BigNumeric(std::pow(e, exp));int count = exp / 700;BigNumeric bgn(std::pow(e, 700.0));for (size_t i = 0; i < count; i++)res = res * bgn;BigNumeric bgn1(std::pow(e, exp - count * 700));res = res * bgn1;return res;}static BigNumeric Vpow(_T e, _T exp){BigNumeric res(1.0);BigNumeric bgnmant(e);int chk = bgnmant.exponent == 0 ? std::abs(exp) : std::abs(exp) * bgnmant.exponent;if (chk <= 300) return BigNumeric(std::pow(e, exp));int count = exp / 300;BigNumeric bgn(std::pow(e, 300.0));for (size_t i = 0; i < count; i++)res = res * bgn;BigNumeric bgn1(std::pow(e, exp - count * 300));res = res * bgn1;return res;}};#endif // !__BigNumeric_h4.测试
//测试
#include "BigNumeric.hpp"int main() {BigNumeric<double> bignum = BigNumeric<double>::Factorial(300);BigNumeric<double> bignum1 = BigNumeric<double>::Epow(1000);bignum = bignum1 / bignum;return 0;
}结果:6.4369310844548986e-181,数字部分精度为 e-12,指数部分完全准确。
相关文章:
大数计算:e^1000/300!
1.问题:大数计算可能超出数据类型范围 当单独计算 ,因为 ,double的最大取值为1.79769e308,所以 肯定超过了double的表示范围。 同样,对于300!也是如此。 那我们应该怎么去计算和存储结果呢?…...
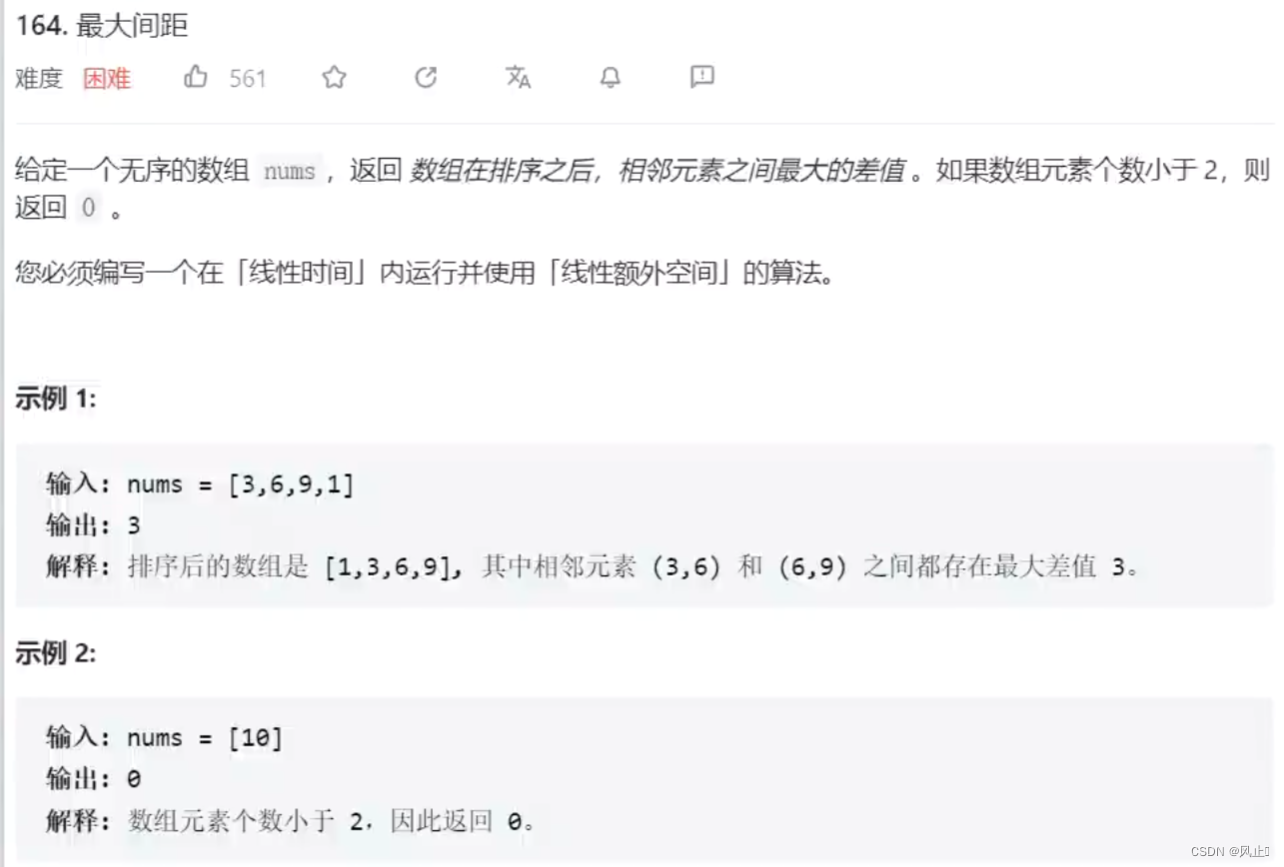
力扣164最大间距
1.前言 因为昨天写了一个基数排序,今天我来写一道用基数排序实现的题解,希望可以帮助你理解基数排序。 这个题本身不难,就是线性时间和线性额外空间(O(n))的算法,有点难实现 基数排序的时间复杂度是O(d*(nradix)),其中…...

聚观早报 | “百度世界2023”即将举办;2024款岚图梦想家上市
【聚观365】10月13日消息 “百度世界2023”即将举办 2024款岚图梦想家上市 腾势D9用户超10万 华为发布新一代GigaGreen Radio OpenAI拟进行重大更新 “百度世界2023”即将举办 “百度世界2023”将于10月17日在北京首钢园举办。届时,百度创始人、董事长兼首席执…...

Windows 应用程序监控重启
执行思路 1.定时关闭可执行程序,2.再通过定时监控启动可执行程序 定时启动关闭程序.bat echo off cd "D:\xxxx\" :: 可执行程序目录 Start "" /b xxxx.exe :: 可执行程序 timeout /T 600 /nobreak >nul :: 600秒 taskkill /IM xxxx.exe /…...
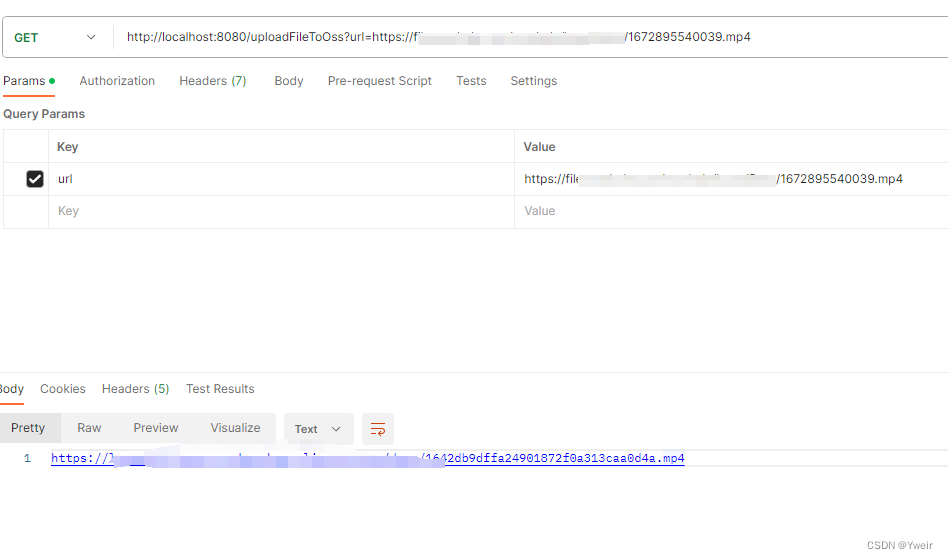
springboot 通过url下载文件并上传到OSS
DEMO流程 传入一个需要下载并上传的url地址下载文件上传文件并返回OSS的url地址 springboot pom文件依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w…...
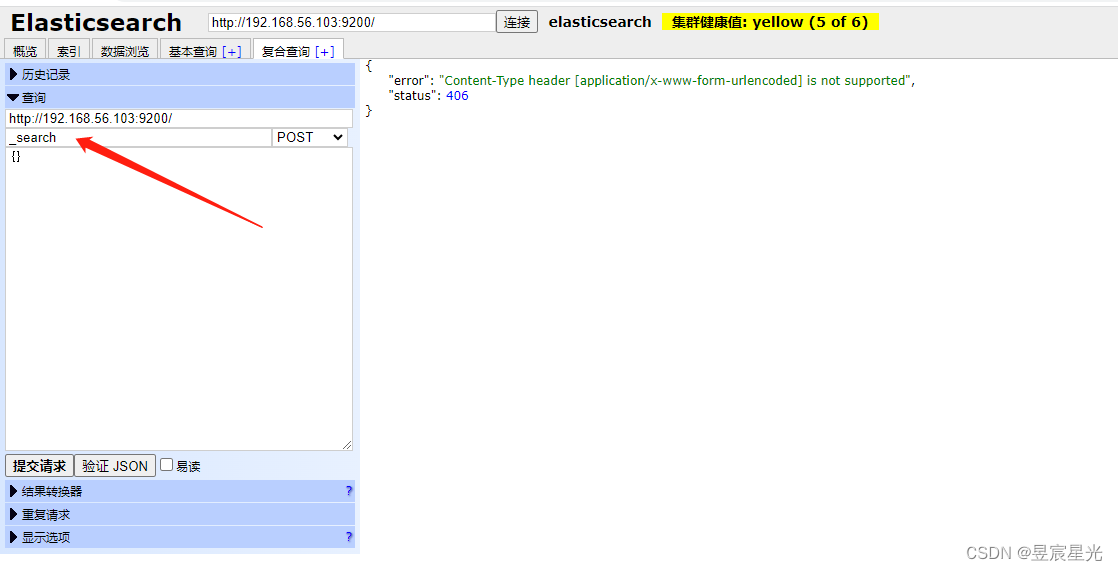
docker创建elasticsearch、elasticsearch-head部署及简单操作
elasticsearch部署 1 拉取elasticsearch镜像 docker pull elasticsearch:7.7.0 2 创建文件映射路径 mkdir /mydata/elasticsearch/data mkdir /mydata/elasticsearch/plugins mkdir /mydata/elasticsearch/config 3 文件夹授权 chmod 777 /mydata/elastic…...
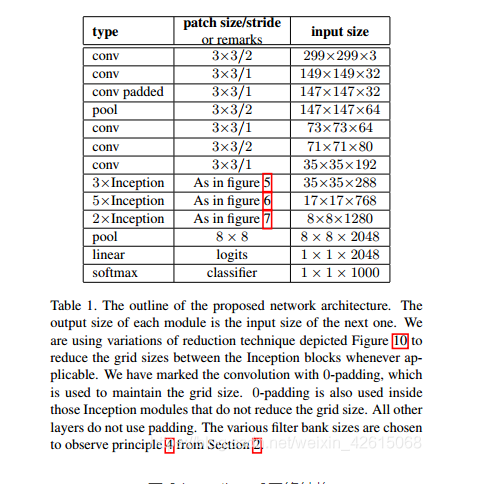
竞赛选题 深度学习+python+opencv实现动物识别 - 图像识别
文章目录 0 前言1 课题背景2 实现效果3 卷积神经网络3.1卷积层3.2 池化层3.3 激活函数:3.4 全连接层3.5 使用tensorflow中keras模块实现卷积神经网络 4 inception_v3网络5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 *…...

Codeforces Round 903 (Div. 3)ABCDE
Codeforces Round 903 (Div. 3)ABCDE 目录 A. Dont Try to Count题目大意思路核心代码 B. Three Threadlets题目大意思路核心代码 C. Perfect Square题目大意思路核心代码 D. Divide and Equalize题目大意思路核心代码 E. Block Sequence题目大意思路核心代码 A. Don’t Try t…...

C# 与 C/C++ 的交互
什么是平台调用 (P/Invoke) P/Invoke 是可用于从托管代码访问非托管库中的结构、回调和函数的一种技术。 托管代码与非托管的区别 托管代码和非托管代码的主要区别是内存管理方式和对计算机资源的访问方式。托管代码通常运行在托管环境中,如 mono 或 java 虚拟机等…...
新版Android Studio搜索不到Lombok以及无法安装Lombok插件的问题
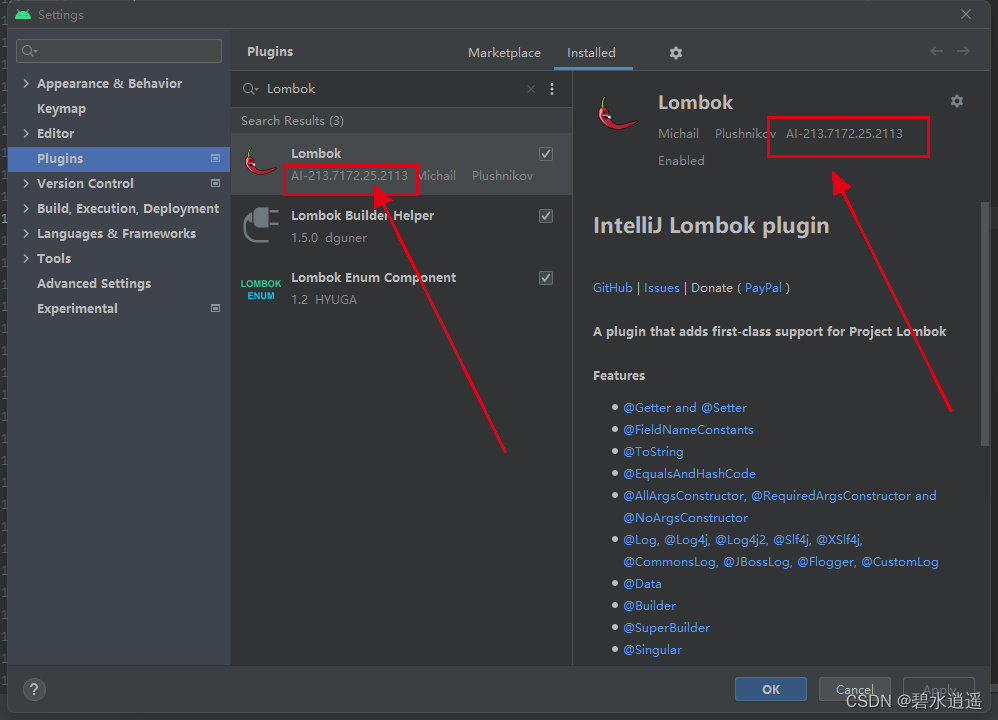
前言 在最近新版本的Android Studio中,使用插件时,在插件市场无法找到Lombox Plugin,具体表现如下图所示: 1、操作步骤: (1)打开Android Studio->Settings->Plugins,搜索Lom…...

BST二叉搜索树
文章目录 概述实现创建节点查找节点增加节点查找后驱值根据关键词删除找到树中所有小于key的节点的value 概述 二叉搜索树,它具有以下的特性,树节点具有一个key属性,不同节点之间key是不能重复的,对于任意一个节点,它…...

【Leetcode】211. 添加与搜索单词 - 数据结构设计
一、题目 1、题目描述 请你设计一个数据结构,支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。 实现词典类 WordDictionary : WordDictionary() 初始化词典对象void addWord(word) 将 word 添加到数据结构中,之后可以对它…...
Discuz户外旅游|旅行游记模板/Discuz!旅行社、旅游行业门户网站模板
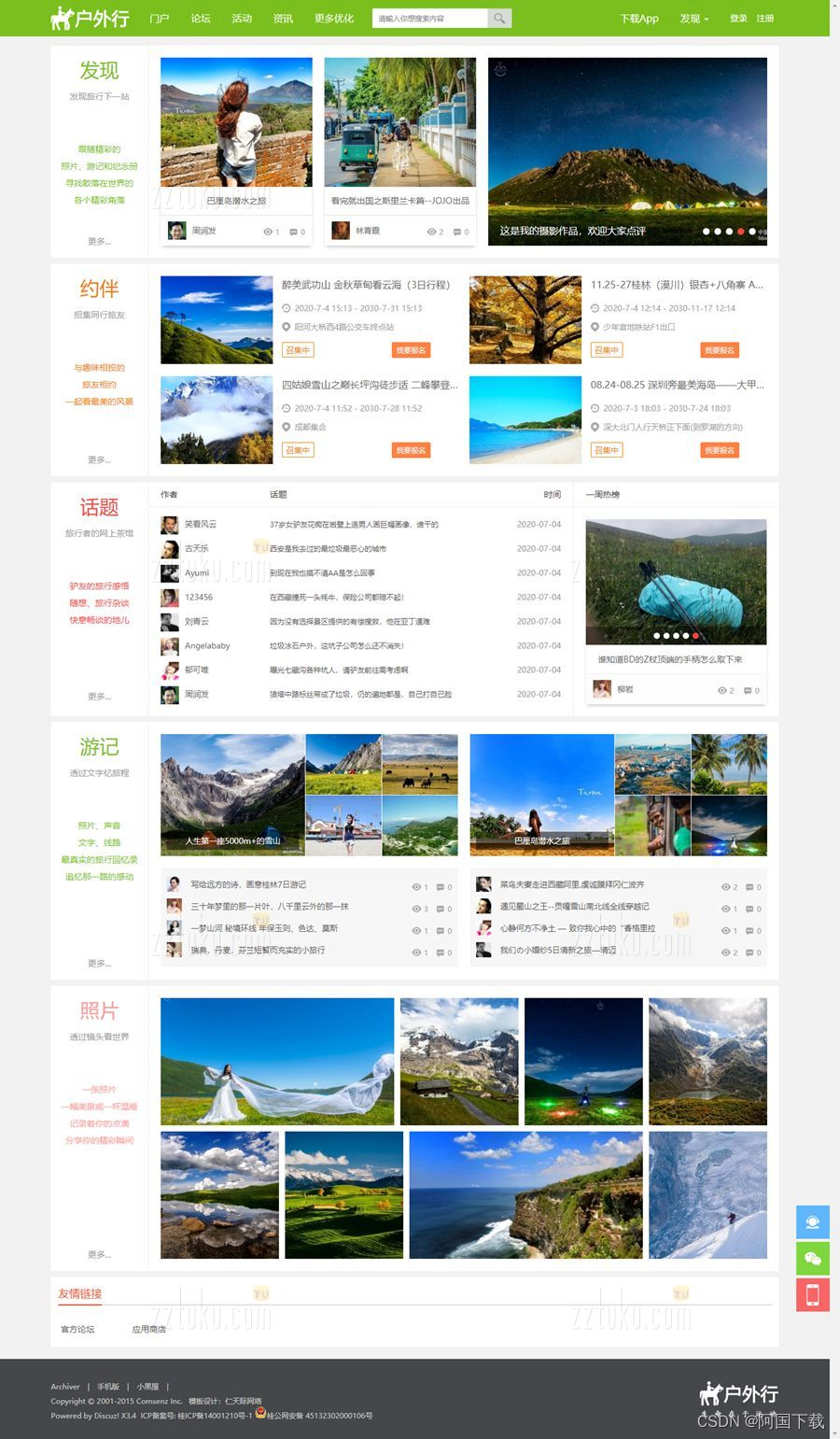
价值328的discuz户外旅游|旅行游记模板,本模板需要配套【仁天际-PC模板管理】插件使用。 模板说明 1、模板页面宽度1200px,简洁大气,较适合户外旅行、骑行、游记、摩旅、旅游、活动等类型的论坛、频道网站; 2、所优化的页面有&…...

【重拾C语言】十一、外部数据组织——文件
目录 前言 十一、外部数据组织——文件 11.1 重新考虑户籍管理问题——文件 11.2 文件概述 11.2.1 文件分类 11.2.2 文件指针、标记及文件操作 11.3 打开、关闭文件 11.4 I/O操作 11.4.1 字符读写 11.4.2 字符串读写 11.4.3 格式化读写 11.4.4 数据块读写 11.4.5 …...
dpdk/spdk/网络协议栈/存储/网关开发/网络安全/虚拟化/ 0vS/TRex/dpvs技术专家成长体系教程
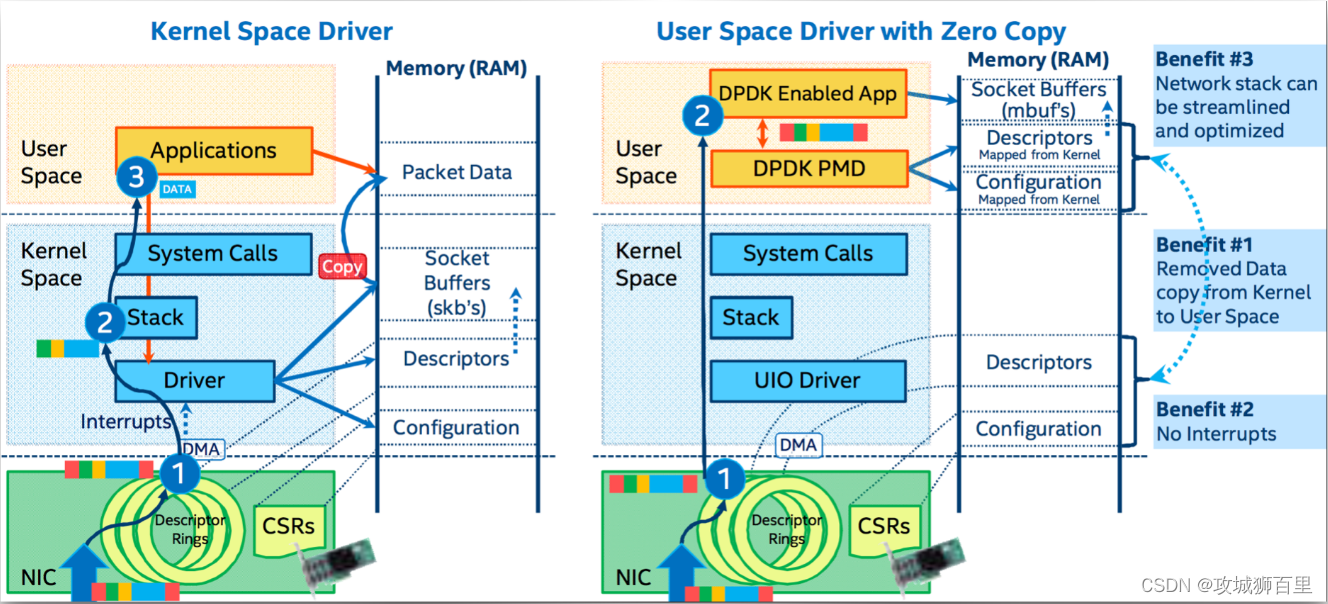
课程围绕安全,网络,存储,云原生4个维度去讲解核心技术点。 6个专栏组成:dpdk网络专栏、存储技术专栏、安全与网关开发专栏、虚拟化与云原生专栏、测试工具专栏、性能测试专栏 一、dpdk网络 dpdk基础知识 多队列网卡࿰…...

树莓派玩转openwrt软路由:5.OpenWrt防火墙配置及SSH连接
1、SSH配置 打开System -> Administration,打开SSH Access将Interface配置成unspecified。 如果选中其他的接口表示仅在给定接口上侦听,如果未指定,则在所有接口上侦听。在未指定下,所有的接口均可通过SSH访问认证。 2、防火…...

Gin:获取本机IP,获取访问IP
获取本机IP func GetLocalIP() []string {var ipStr []stringnetInterfaces, err : net.Interfaces()if err ! nil {fmt.Println("net.Interfaces error:", err.Error())return ipStr}for i : 0; i < len(netInterfaces); i {if (netInterfaces[i].Flags & ne…...

缓存降级代码结构设计
缓存降级设计思想 接前文缺陷点 本地探针应该增加计数器,多次异常再设置,避免网络波动造成误判。耦合度过高,远端缓存和本地缓存应该平行关系被设计为上下游关系了。公用的远端缓存的操作方法应该私有化,避免集成方代码误操作&…...

一文深入理解高并发服务器性能优化
我们现在已经搞定了 C10K并发连接问题 ,升级一下,如何支持千万级的并发连接?你可能说,这不可能。你说错了,现在的系统可以支持千万级的并发连接,只不过所使用的那些激进的技术,并不为人所熟悉。…...

pytorch中的归一化函数
在 PyTorch 的 nn 模块中,有一些常见的归一化函数,用于在深度学习模型中进行数据的标准化和归一化。以下是一些常见的归一化函数: nn.BatchNorm1d, nn.BatchNorm2d, nn.BatchNorm3d: 这些函数用于批量归一化 (Batch Normalization…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...
