BST二叉搜索树
文章目录
- 概述
- 实现
- 创建节点
- 查找节点
- 增加节点
- 查找后驱值
- 根据关键词删除
- 找到树中所有小于key的节点的value
概述
二叉搜索树,它具有以下的特性,树节点具有一个key属性,不同节点之间key是不能重复的,对于任意一个节点,它的key都要比左子树的key大,比右子树的key小
实现
创建节点
static class BSTNode {int key;Object value;BSTNode left;BSTNode right;public BSTNode(int key, Object value) {this.key = key;this.value = value;}public BSTNode(int key, Object value, BSTNode left, BSTNode right) {this.key = key;this.value = value;this.left = left;this.right = right;}}
查找节点
利用二叉树的性质
public Object get(int key) {BSTNode node = root;while (node != null) {if (node.key < key) {node = node.right;} else if (node.key > key) {node = node.left;} else {return node.value;}}return null;}
增加节点
同样利用二叉树的性质,但是需要记录要增加的节点的父节点
public void put(int key, Object value) {BSTNode node = root;BSTNode parent = null;while (node != null) {parent = node;if (key < node.key) {node = node.left;} else if (key > node.key) {node = node.right;} else {//直接修改node.value = value;return;}}if (parent == null) {root = new BSTNode(key, value);} else if (key > parent.key) {parent.right = new BSTNode(key, value);} else {parent.left = new BSTNode(key, value);}}
查找后驱值
在后面的AVL,以及红黑树中删除节点是,我们经常会需要求一个节点的后驱节点
分类讨论,分成两种情况
若节点有右子树,那么右子树的最小值就是前驱
若没有右子树,则去寻找是否存在从右而来的祖先节点,最近的这个祖先节点就是后驱
两种情况都不满足,则该节点没有后驱
public Object predecessor(int key) {BSTNode ancestorFromRight = null;BSTNode node = root;while (node != null) {if (key < node.key) {ancestorFromRight = node;node = node.left;} else if (key > node.key) {node = node.right;} else {break;}}//没有该节点if (node == null) {return null;}if (node.right != null) {return min(node.right);}return ancestorFromRight == null ? null : ancestorFromRight.value;}public Object min(BSTNode node) {if (node == null) {return null;}while (node.left != null) {node = node.left;}return node.value;}
根据关键词删除
根据关键字删除
删除有一下几种情况
第一种:删除节点没有右孩子,将左孩子挂过去
第二种:删除节点没有左孩子,将右孩子挂过去
第三种:都没有,挂过去null
第四种:左右孩子都有,可以将后继节点挂在parent后面,后继节点为s,后继节点的父亲为sp
1.将如果sp就是要删除的节点
2.sp不是删除节点,需要将s的后代给sp
public Object delete(int key) {BSTNode node = root;BSTNode parent = null;while (node != null) {if (key < node.key) {parent = node;node = node.left;} else if (key > node.key) {parent = node;node = node.right;} else {break;}}if (node == null) {return null;}if (node.left == null) {//情况1shift(parent, node, node.right);//情况2} else if (node.right == null) {shift(parent, node, node.left);} else {BSTNode s = node.right;BSTNode sParent = node;while (s.left != null) {sParent = s;s = s.left;}if (sParent != node) {//将后驱节点的孩子挂在后驱节点父亲的后面shift(sParent, s, s.right);s.right = node.right;}//后驱节点一定没有左孩子,所以可以直接的挂靠shift(parent, node, s);s.left = node.left;}return node.value;}/** 托孤方法** */private void shift(BSTNode parent, BSTNode deleted, BSTNode child) {if (parent == null) {root = child;} else if (deleted == parent.left) {parent.left = child;} else {parent.right = child;}}
找到树中所有小于key的节点的value
我们可以通过一个中序遍历实现,对于一个二叉搜索树来说,中序遍历的结果,恰好是从小到大排序的
public List<Object> less(int key) {ArrayList<Object> result = new ArrayList<>();LinkedList<BSTNode> stack = new LinkedList<>();BSTNode node = root;while (node != null || !stack.isEmpty()) {if (node != null) {stack.push(node);node = node.left;} else {BSTNode min = stack.pop();if (min.key < key) {result.add(min.value);} else {break;}node = min.right;}}return result;}
相关文章:

BST二叉搜索树
文章目录 概述实现创建节点查找节点增加节点查找后驱值根据关键词删除找到树中所有小于key的节点的value 概述 二叉搜索树,它具有以下的特性,树节点具有一个key属性,不同节点之间key是不能重复的,对于任意一个节点,它…...

【Leetcode】211. 添加与搜索单词 - 数据结构设计
一、题目 1、题目描述 请你设计一个数据结构,支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。 实现词典类 WordDictionary : WordDictionary() 初始化词典对象void addWord(word) 将 word 添加到数据结构中,之后可以对它…...
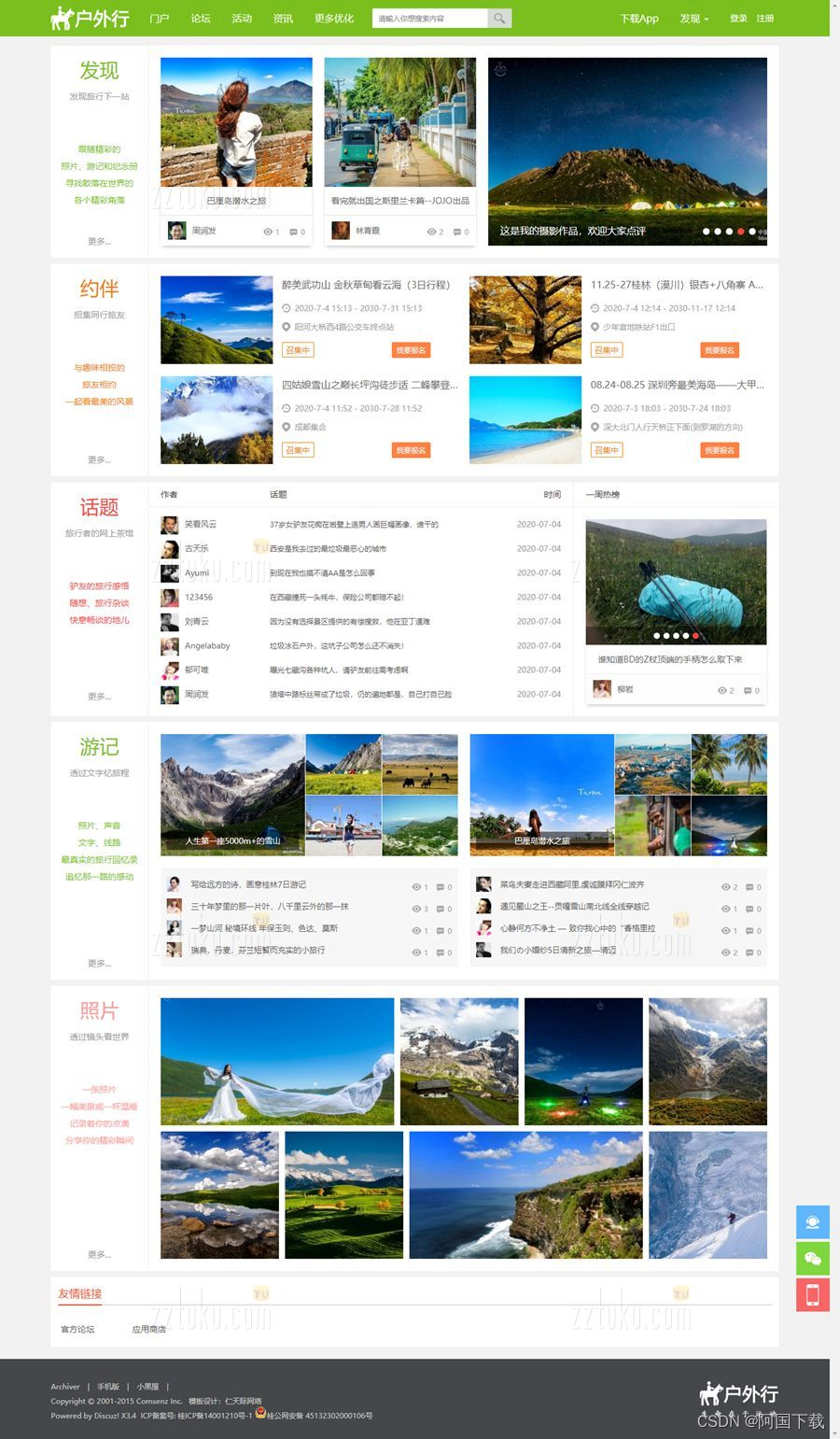
Discuz户外旅游|旅行游记模板/Discuz!旅行社、旅游行业门户网站模板
价值328的discuz户外旅游|旅行游记模板,本模板需要配套【仁天际-PC模板管理】插件使用。 模板说明 1、模板页面宽度1200px,简洁大气,较适合户外旅行、骑行、游记、摩旅、旅游、活动等类型的论坛、频道网站; 2、所优化的页面有&…...

【重拾C语言】十一、外部数据组织——文件
目录 前言 十一、外部数据组织——文件 11.1 重新考虑户籍管理问题——文件 11.2 文件概述 11.2.1 文件分类 11.2.2 文件指针、标记及文件操作 11.3 打开、关闭文件 11.4 I/O操作 11.4.1 字符读写 11.4.2 字符串读写 11.4.3 格式化读写 11.4.4 数据块读写 11.4.5 …...
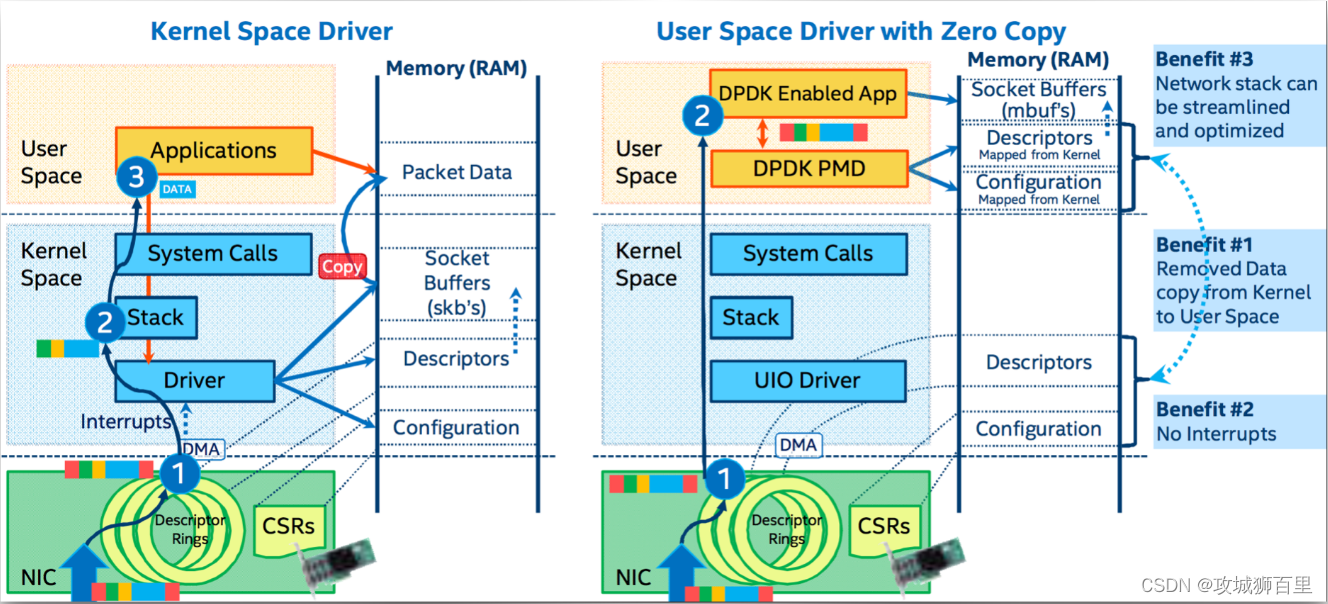
dpdk/spdk/网络协议栈/存储/网关开发/网络安全/虚拟化/ 0vS/TRex/dpvs技术专家成长体系教程
课程围绕安全,网络,存储,云原生4个维度去讲解核心技术点。 6个专栏组成:dpdk网络专栏、存储技术专栏、安全与网关开发专栏、虚拟化与云原生专栏、测试工具专栏、性能测试专栏 一、dpdk网络 dpdk基础知识 多队列网卡࿰…...

树莓派玩转openwrt软路由:5.OpenWrt防火墙配置及SSH连接
1、SSH配置 打开System -> Administration,打开SSH Access将Interface配置成unspecified。 如果选中其他的接口表示仅在给定接口上侦听,如果未指定,则在所有接口上侦听。在未指定下,所有的接口均可通过SSH访问认证。 2、防火…...

Gin:获取本机IP,获取访问IP
获取本机IP func GetLocalIP() []string {var ipStr []stringnetInterfaces, err : net.Interfaces()if err ! nil {fmt.Println("net.Interfaces error:", err.Error())return ipStr}for i : 0; i < len(netInterfaces); i {if (netInterfaces[i].Flags & ne…...

缓存降级代码结构设计
缓存降级设计思想 接前文缺陷点 本地探针应该增加计数器,多次异常再设置,避免网络波动造成误判。耦合度过高,远端缓存和本地缓存应该平行关系被设计为上下游关系了。公用的远端缓存的操作方法应该私有化,避免集成方代码误操作&…...

一文深入理解高并发服务器性能优化
我们现在已经搞定了 C10K并发连接问题 ,升级一下,如何支持千万级的并发连接?你可能说,这不可能。你说错了,现在的系统可以支持千万级的并发连接,只不过所使用的那些激进的技术,并不为人所熟悉。…...

pytorch中的归一化函数
在 PyTorch 的 nn 模块中,有一些常见的归一化函数,用于在深度学习模型中进行数据的标准化和归一化。以下是一些常见的归一化函数: nn.BatchNorm1d, nn.BatchNorm2d, nn.BatchNorm3d: 这些函数用于批量归一化 (Batch Normalization…...

【管理运筹学】第 10 章 | 排队论(1,排队论的基本概念)
文章目录 引言一、基本概念1.1 排队过程1.2 排队系统的组成和特征1.3 排队模型的分类1.4 系统指标1.5 系统状态 引言 开一点排队论的内容吧,方便做题。 排队论(Queuing Theory)也称随机服务系统理论,是为解决一系列排队问题&…...

【Express】服务端渲染(模板引擎 EJS)
EJS(Embedded JavaScript)是一款流行的模板引擎,可以用于在Express中创建动态的HTML页面。它允许在HTML模板中嵌入JavaScript代码,并且能够生成基于数据的动态内容。 下面是一个详细的讲解和示例,演示如何在Express中…...

Linux CentOS8安装gitlab_ce步骤
1 下载安装包 wget --content-disposition https://packages.gitlab.com/gitlab/gitlab-ce/packages/el/8/gitlab-ce-15.0.2-ce.0.el8.x86_64.rpm/download.rpm2 安装gitlab yum install policycoreutils-python-utilsrpm -Uvh gitlab-ce-15.0.2-ce.0.el8.x86_64.rpm3 更新配…...
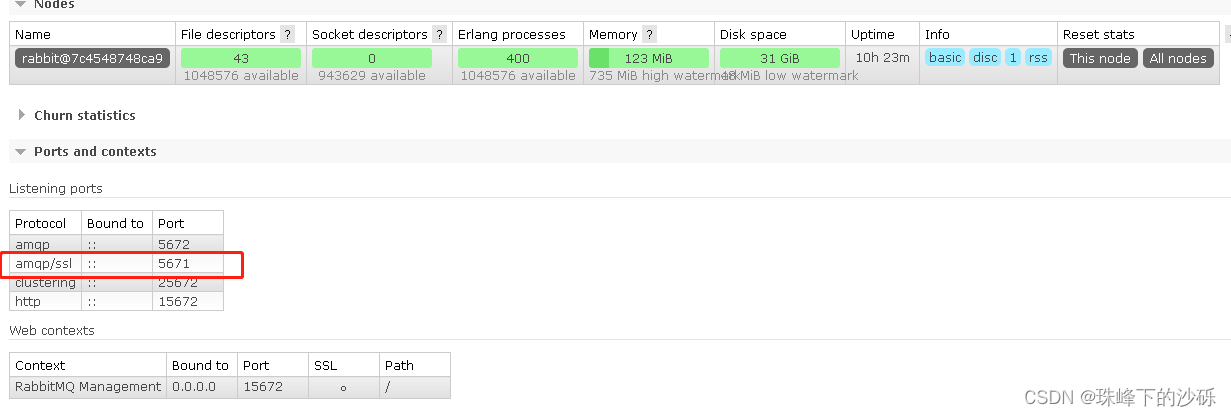
RabbitMq启用TLS
Windows环境 查看配置文件的位置 选择使用的节点 查看当前节点配置文件的配置 配置TLS 将证书放到同配置相同目录中 编辑配置文件添加TLS相关配置 [{ssl, [{versions, [tlsv1.2]}]},{rabbit, [{ssl_listeners, [5671]},{ssl_options, [{cacertfile,"C:/Users/17126…...
CakePHP 3.x/4.x反序列化RCE链
最近网上公开了cakephp一些反序列化链的细节,但是没有公开poc,并且网上关于cakephp的反序列化链比较少,于是自己跟一下 ,构造pop链。 CakePHP简介 CakePHP是一个运用了诸如ActiveRecord、Association Data Mapping、Front Contr…...

练习之C++[3]
文章目录 1.模板类2.模板声明3.string类 1.模板类 模板可以具有非类型参数,用于指定大小,可以根据指定的大小创建动态结构所以可用来创建动态增长和减小的数据结构模板运行时不检查数据类型,也不保证类型安全,相当于类型的宏替换…...

[MT8766][Android12] 修改WIFI热点默认名称、密码、IP地址以及默认开启热点
文章目录 开发平台基本信息问题描述解决方法 开发平台基本信息 芯片: MTK8766 版本: Android 12 kernel: msm-4.19 问题描述 最近做了一款没有屏幕显示的智能盒子,要想操控这款设备就只能通过adb投屏,如果默认不允许有线连接,那么要怎么实…...
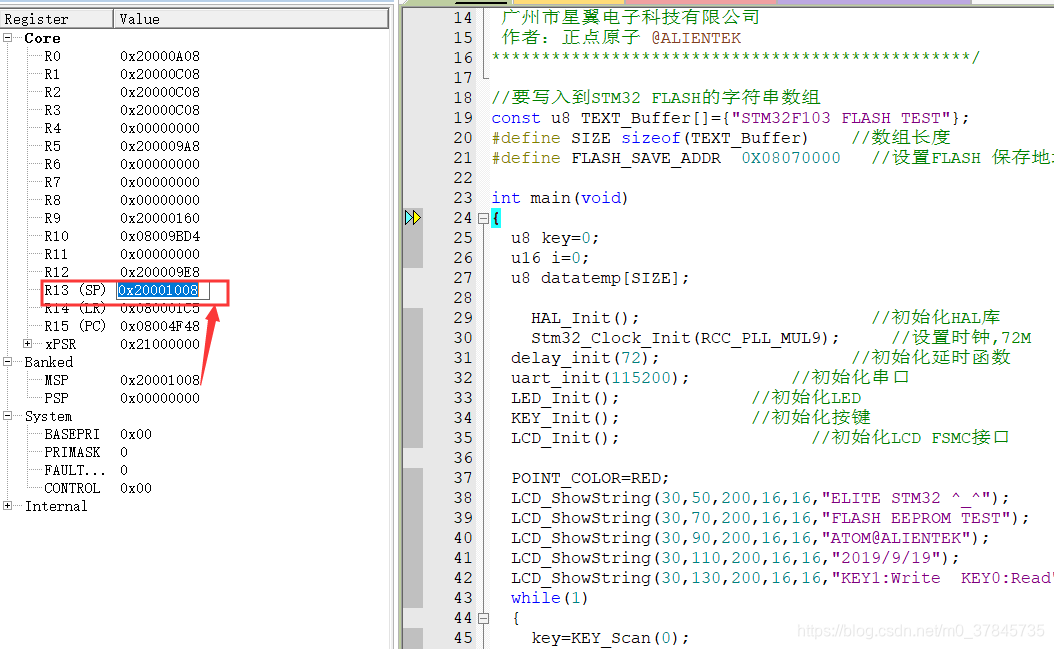
【嵌入式】堆栈与单片机内存
堆栈 在片内RAM中,常常要指定一个专门的区域来存放某些特别的数据 它遵循顺序存取和后进先出(LIFO/FILO)的原则,这个RAM区叫堆栈。 其实堆栈就是单片机中的一些存储单元,这些存储单元被指定保存一些特殊信息,比如地址࿰…...

十大排序算法Java实现及时间复杂度
文章目录 十大排序算法选择排序冒泡排序插入排序希尔排序快速排序归并排序堆排序计数排序基数排序桶排序时间复杂度 参考资料 十大排序算法 选择排序 原理 从待排序的数据元素中找出最小或最大的一个元素,存放在序列的起始位置, 然后再从剩余的未排序元…...

[Go]配置国内镜像源
配置 Windows 选一个 go env -w GOPROXYhttps://goproxy.cn,direct go env -w GOPROXYhttps://mirrors.aliyun.com/goproxy,direct查看环境配置 go env...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
