【管理运筹学】第 10 章 | 排队论(1,排队论的基本概念)
文章目录
- 引言
- 一、基本概念
- 1.1 排队过程
- 1.2 排队系统的组成和特征
- 1.3 排队模型的分类
- 1.4 系统指标
- 1.5 系统状态
引言
开一点排队论的内容吧,方便做题。
排队论(Queuing Theory)也称随机服务系统理论,是为解决一系列排队问题(如日常购物结算排队、电话占线问题、车站堵塞和疏导问题等)而发展的一门学科。
一、基本概念
1.1 排队过程
下图是排队过程的一般模型。来自顾客源(总体)的顾客到达服务机构(服务台)前排队等候服务,接受服务后离开。排队结构指队列的数目和排队方式,排队规则和服务规则说明顾客在排队系统中按怎样的规则、次序接受服务。排队系统包括下图中虚线所包括的部分。

1.2 排队系统的组成和特征
一般的排队系统都由输入过程、排队规则、服务机构 3 个基本部分组成。
1. 输入过程
输入过程是描述顾客来源以及顾客按什么规律到达排队系统的,它包括以下三个方面:
(1)顾客来源。顾客总体的组成可能是有限的,也可能是无限的。
(2)顾客到达方式。顾客到来可能是一个个的,也可能是成批的。
(3)顾客流的概率分布。顾客一个(批)一个(批)来到排队系统,相继到达的顾客之间的间隔时间分布是确定的还是随机的,分布参数是什么,到达的间隔时间是否相互独立,分布是随时间变化还是平稳的。
2. 排队规则
排队规则是描述顾客来到服务系统时,服务机构是否允许排队,顾客是否愿意排队,在排队等待情况下服务的顺序是什么?一般可分为损失制、等待制和混合制三大类。
损失制:顾客到达时,如果所有的服务台均被占用,且服务机构由不允许顾客等待,顾客只能离去。
等待制:顾客达到时,如果所有服务台均被占用,这是顾客自动加入队列等待服务,服务完才离开。有先到先服务、后到先服务、随机服务和优先服务等情形。
3. 服务机构
服务机构主要描述服务台的数目即服务规律。服务机构由多个时,服务方式有并列的、串列的、还有混合的;接受服务的顾客可以是单个的也可以是成批的;服务时间可以是固定的,也可以是随机的;顾客接受服务的时间是否独立等。
1.3 排队模型的分类
为描述排队系统,1953 年 D.G.Kendall 提出了一个分类办法,考虑了排队系统中最主要的、影响最大的三个因素:顾客相继到达的间隔时间分布、服务时间的分布、服务台个数。
按照这三个特征用一定符号表示随机服务系统的种类,称为 Kendall 符号,符号形式为: X / Y / Z X/Y/Z X/Y/Z 其中, X X X 处填写顾客相继到达间隔时间的分布; Y Y Y 处填写服务时间的分布; Z Z Z 处填写并列的服务台个数。
一般表示相继到达间隔时间和服务时间分布的随机分布符号是:
M M M —— 负指数分布(Markov);
D D D —— 确定性(Deterministic);
E k E_k Ek —— k k k 阶爱尔朗(Erlang)分布;
G I GI GI —— 一般相互独立(General Independent);
G G G —— 一般服务时间的分布。
例如, M / M / 1 M/M/1 M/M/1 表示到达间隔时间服从负指数分布、服务时间服从负指数分布、单服务台的模型; D / M / c D/M/c D/M/c 表示到达间隔时间确定、服务时间服从负指数分布、 c c c 个平行服务台(顾客是一队)的模型。
1971 年关于排队论符号标准化会议上决定,将 Kendall 符号进行扩充,表示成 X / Y / Z / A / B / C X/Y/Z/A/B/C X/Y/Z/A/B/C 。其中前三项意义不变,而 A A A 表示系统容量限制 N N N ; B B B 表示顾客源数目 m m m ; C C C 处填写服务规则,如先到先服务(FCFS,first come first serve)。
并约定,如果省略后三项,指的是 X / Y / Z / ∞ / ∞ / F C F S X/Y/Z/\infty/\infty/FCFS X/Y/Z/∞/∞/FCFS 的情形。考试范围,只讨论 FCFS 的情形,故第六项也可省略。
1.4 系统指标
研究排队系统的目的,是把握排队系统运行的效率,估计服务质量,确定系统参数的最优值,最终目的是确定排队系统的结构是否合理以及设计改进措施等,所以必须确定用以判断系统运行优劣的基本数量指标,有如下这些。
- 队长,指在系统中的顾客数(包括在队列中等待服务的顾客和正在接受服务的顾客),它的期望值记作 L s L_s Ls ;
- 排队长,指在系统中排队等候服务的顾客数,它的期望值记作 L q L_q Lq ;
- 逗留时间,指一个顾客在排队系统的停留时间,它的期望值记作 W s W_s Ws ;
- 等待时间,指一个顾客在系统中排队等候的时间,它的期望值记作 W q W_q Wq 。
在机器故障问题中,无论是等待修理或正在修理,都会使工厂受到损失,因此逗留时间(停工时间)是最被关心的;而一般购物、诊断等排队问题中,顾客常关心的是等待时间。
忙期(Busy Period)是指从顾客到达空闲的服务机构起到服务机构再次变为空闲为止的这段时间的长度,即服务机构连续繁忙的时间长度,它关系到服务员的工作强度。忙期和一个忙期中平均完成服务的顾客数都是衡量服务机构效率的指标。
在即时制或排队有限制的情形,由于顾客被拒绝而使企业受到损失的损失率及以后经常遇到的服务强度等,都是很重要的指标。
1.5 系统状态
系统状态指的是系统中的顾客数,如系统中有 n n n 个顾客,就说系统的状态是 n n n ,它的可能值是:
- 队长无限制时, n = 0 , 1 , 2 , ⋯ ; n=0,1,2,\cdots; n=0,1,2,⋯;
- 队长有限制且最大数为 N N N 时, n = 0 , 1 , 2 , ⋯ , N ; n=0,1,2,\cdots,N; n=0,1,2,⋯,N;
- 即时制,服务台个数是 c c c 时, n = 0 , 1 , 2 , ⋯ , c n=0,1,2,\cdots,c n=0,1,2,⋯,c 。
系统状态的概率一般是随时刻 t t t 变化的,时刻 t t t 、状态为 n n n 的概率用 P n ( t ) P_n(t) Pn(t) 表示。
计算状态概率 P n ( t ) P_n(t) Pn(t) ,首先要建立起含 P n ( t ) P_n(t) Pn(t) 的关系式,因 t t t 是连续变量,而 n n n 只能取非负整数,所以一般 P n ( t ) P_n(t) Pn(t) 的关系式为差分微分方程(关于 t t t 的微分方程,关于 n n n 的差分方程)。方程的解称为瞬态(或过渡状态,Transient State)解。求瞬态解比较困难,即使求出也很难利用,因此常用它的极限(如果存在) lim t → ∞ p n ( t ) = p n . \lim_{t\to\infty}p_n(t)=p_n. t→∞limpn(t)=pn. 称其为稳态(Steady State),或称为平衡状态(Statistical Equilibrium State)的解。
稳态的物理含义是,当系统运行了无限长时间后,初始( t = 0 t=0 t=0)状态的概率分布( P n ( 0 ) , n ≥ 0 P_n(0),n\geq0 Pn(0),n≥0)的影响将消失,而且系统的状态概率分布不再随时间变化。在实际应用中,大多数系统会很快趋于稳态(如下图所示),而无须等到 t → ∞ t\to\infty t→∞ 。但永远达不到稳态的情形也是存在的。

求稳态概率 P n ( t ) P_n(t) Pn(t) 时,不一定求 t → ∞ t\to\infty t→∞ 时 P n ( t ) P_n(t) Pn(t) 的极限,而只需对时间的一阶导 P n ′ ( t ) = 0 P'_n(t)=0 Pn′(t)=0 即可。
相关文章:

【管理运筹学】第 10 章 | 排队论(1,排队论的基本概念)
文章目录 引言一、基本概念1.1 排队过程1.2 排队系统的组成和特征1.3 排队模型的分类1.4 系统指标1.5 系统状态 引言 开一点排队论的内容吧,方便做题。 排队论(Queuing Theory)也称随机服务系统理论,是为解决一系列排队问题&…...

【Express】服务端渲染(模板引擎 EJS)
EJS(Embedded JavaScript)是一款流行的模板引擎,可以用于在Express中创建动态的HTML页面。它允许在HTML模板中嵌入JavaScript代码,并且能够生成基于数据的动态内容。 下面是一个详细的讲解和示例,演示如何在Express中…...

Linux CentOS8安装gitlab_ce步骤
1 下载安装包 wget --content-disposition https://packages.gitlab.com/gitlab/gitlab-ce/packages/el/8/gitlab-ce-15.0.2-ce.0.el8.x86_64.rpm/download.rpm2 安装gitlab yum install policycoreutils-python-utilsrpm -Uvh gitlab-ce-15.0.2-ce.0.el8.x86_64.rpm3 更新配…...
RabbitMq启用TLS
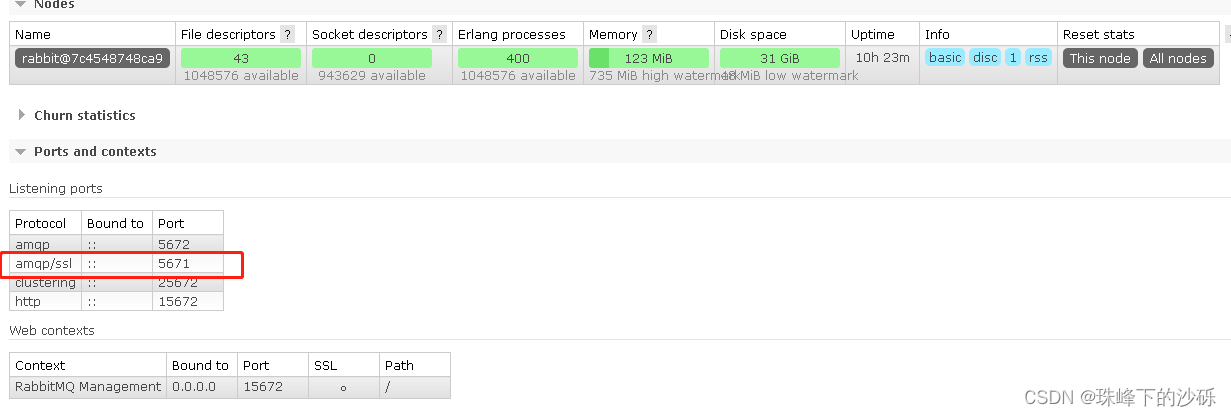
Windows环境 查看配置文件的位置 选择使用的节点 查看当前节点配置文件的配置 配置TLS 将证书放到同配置相同目录中 编辑配置文件添加TLS相关配置 [{ssl, [{versions, [tlsv1.2]}]},{rabbit, [{ssl_listeners, [5671]},{ssl_options, [{cacertfile,"C:/Users/17126…...
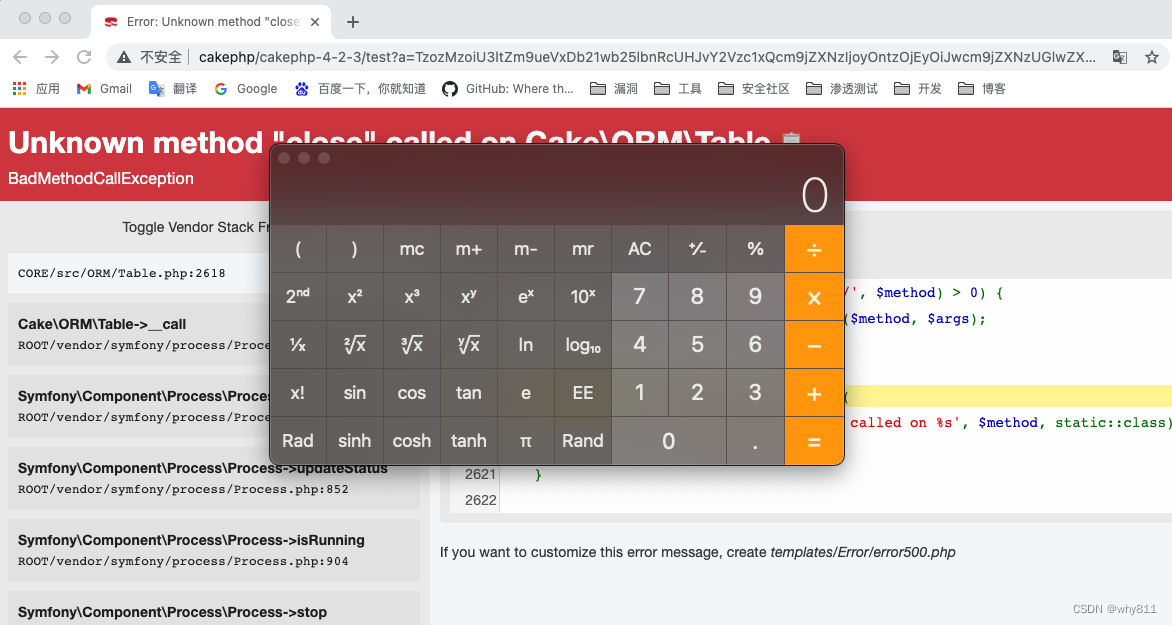
CakePHP 3.x/4.x反序列化RCE链
最近网上公开了cakephp一些反序列化链的细节,但是没有公开poc,并且网上关于cakephp的反序列化链比较少,于是自己跟一下 ,构造pop链。 CakePHP简介 CakePHP是一个运用了诸如ActiveRecord、Association Data Mapping、Front Contr…...

练习之C++[3]
文章目录 1.模板类2.模板声明3.string类 1.模板类 模板可以具有非类型参数,用于指定大小,可以根据指定的大小创建动态结构所以可用来创建动态增长和减小的数据结构模板运行时不检查数据类型,也不保证类型安全,相当于类型的宏替换…...

[MT8766][Android12] 修改WIFI热点默认名称、密码、IP地址以及默认开启热点
文章目录 开发平台基本信息问题描述解决方法 开发平台基本信息 芯片: MTK8766 版本: Android 12 kernel: msm-4.19 问题描述 最近做了一款没有屏幕显示的智能盒子,要想操控这款设备就只能通过adb投屏,如果默认不允许有线连接,那么要怎么实…...
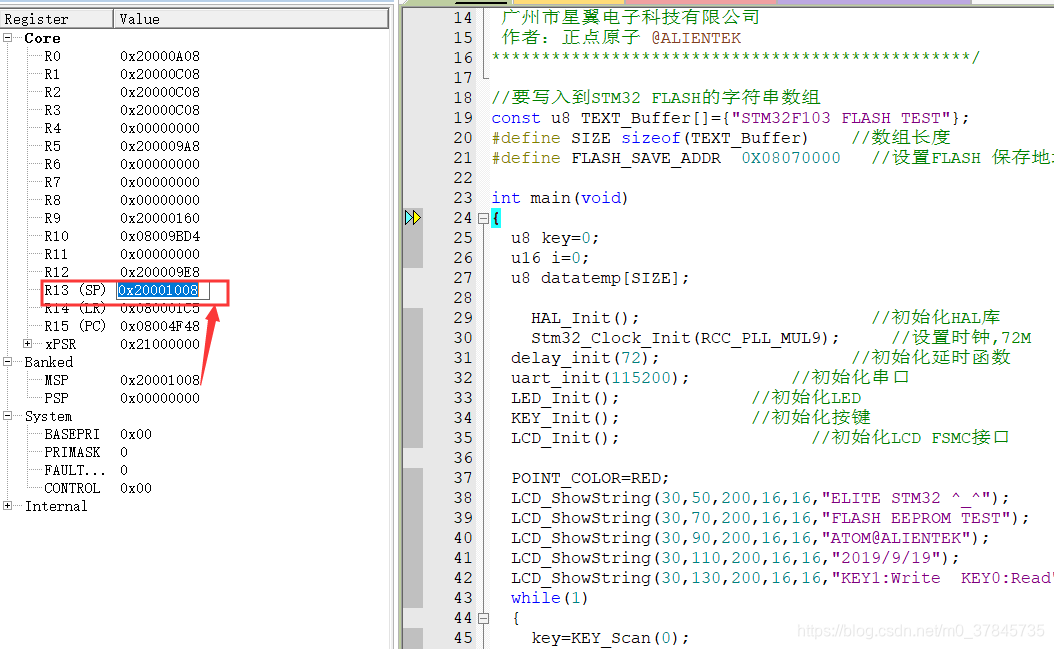
【嵌入式】堆栈与单片机内存
堆栈 在片内RAM中,常常要指定一个专门的区域来存放某些特别的数据 它遵循顺序存取和后进先出(LIFO/FILO)的原则,这个RAM区叫堆栈。 其实堆栈就是单片机中的一些存储单元,这些存储单元被指定保存一些特殊信息,比如地址࿰…...

十大排序算法Java实现及时间复杂度
文章目录 十大排序算法选择排序冒泡排序插入排序希尔排序快速排序归并排序堆排序计数排序基数排序桶排序时间复杂度 参考资料 十大排序算法 选择排序 原理 从待排序的数据元素中找出最小或最大的一个元素,存放在序列的起始位置, 然后再从剩余的未排序元…...

[Go]配置国内镜像源
配置 Windows 选一个 go env -w GOPROXYhttps://goproxy.cn,direct go env -w GOPROXYhttps://mirrors.aliyun.com/goproxy,direct查看环境配置 go env...

Java知识点补充
静态方法 vs 实例方法: 静态方法(使用 static 关键字声明):属于类,不依赖于对象实例,可以通过类名直接调用。 实例方法(不使用 static 关键字声明):属于类的实例…...
Webpack和JShaman相比有什么不同?
Webpack和JShaman相比有什么不同? Webpack的功能是打包,可以将多个JS文件打包成一个JS文件。 JShaman专门用于对JS代码混淆加密,目的是让JavaScript代码变的不可读、混淆功能逻辑、加密代码中的隐秘数据或字符,是用于代码保护的…...
WEB应用程序编程接口API
使用Web API Web API是网站的一部分,用于与使用具体URL请求特定信息的程序交互。这种请求称为API调用。请求的数据格式以易于处理的格式(JSON,CSV)返回。 Git和GitHub Git是一个分布式版本控制系统,帮助人们管理为项目所做的工作…...

进阶JAVA篇- BigDecimal 类的常用API(四)
目录 API 1.0 BigDecimal 类说明 1.1 为什么浮点数会计算不精确呢? 1.2 如何创建 BigDecimal 类型的对象 1.2.1具体来介绍三种方式来创建: 1.2.2 结合三种创建方法,一起来分析一下。 1.3 BigDecimal 类中的 valueOf(Strin…...
UE4 顶点网格动画播放后渲染模糊问题
问题描述:ABC格式的顶点网格动画播放结束后,改模型看起来显得很模糊有抖动的样子 解决办法:关闭逐骨骼动态模糊...

centos 磁盘挂载与解挂
磁盘挂载 查看已挂载的磁盘 df -TH查看磁盘分区,对比第一步,看哪些磁盘没有挂载,例如发现/dev/sdb的磁盘没有在第一步中显示 fdisk -l磁盘分区(/dev/sdb为上一步骤中没有挂载的磁盘) fdisk /dev/sdb执行上一命令后…...

C语言 位操作
定义 位操作提高程序运行效率,减少除法和取模的运算。在计算机程序中,数据的位是可以操作的最小数据单位,理论上可以用“位运算”来完成所有的运算和操作。 左移 后空缺自动补0 右移 分为逻辑右移和算数右移 逻辑右移 不管什么类型&am…...

Go语言中入门Hello World以及IDE介绍
您可以阅读Golang教程第1部分:Go语言介绍与安装 来了解什么是golang以及如何安装golang。 Go语言已经安装好了,当你开始学习Go语言时,编写一个"Hello, World!"程序是一个很好的入门点。 下面将会提供了一些有关IDE和在线编辑器的…...
)
Java面试题-Java核心基础-第二天(基本语法)
目录 一、注释有几种形式 二、标识符与关键字的区别 三、自增自减运算符 四、移位运算符 五、continue、break、return的区别 一、注释有几种形式 注释除了有其他编程语言有的单行注释和多行注释之外,还有其Java特有的文档注释 文档注释能够使用javadoc命令就…...
Linux 部署 GitLab idea 连接
概述 GitLab 是一个开源的代码管理平台,使用 Git 作为版本控制工具,提供了 Web 界面和多种功能,如 wiki、issue 跟踪、CI/CD 等。 GitLab 可以自托管或使用 SaaS 服务,支持多种操作系统和执行器。 GitLab 可以帮助软件开发团队…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
