【Leetcode】211. 添加与搜索单词 - 数据结构设计
一、题目
1、题目描述
请你设计一个数据结构,支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。
实现词典类 WordDictionary :
WordDictionary()初始化词典对象void addWord(word)将word添加到数据结构中,之后可以对它进行匹配bool search(word)如果数据结构中存在字符串与word匹配,则返回true;否则,返回false。word中可能包含一些'.',每个.都可以表示任何一个字母。
示例:
输入:
["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
[[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
输出:
[null,null,null,null,false,true,true,true]解释:
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // 返回 False
wordDictionary.search("bad"); // 返回 True
wordDictionary.search(".ad"); // 返回 True
wordDictionary.search("b.."); // 返回 True
提示:
1 <= word.length <= 25addWord中的word由小写英文字母组成search中的word由'.'或小写英文字母组成- 最多调用 104 次
addWord和search
2、基础框架
class WordDictionary {
public:WordDictionary() {}void addWord(string word) {}bool search(string word) {}
};/*** Your WordDictionary object will be instantiated and called as such:* WordDictionary* obj = new WordDictionary();* obj->addWord(word);* bool param_2 = obj->search(word);*/
3、原题链接
211. 添加与搜索单词 - 数据结构设计
二、解题报告
1、思路分析
主要思路同【Leetcode】208.实现Trie(前缀树),但是需要注意,插入的时候只有小写字母字符,而查找的时候有"."和小写字母字符,所以遇到 “.” 字符时,所有子孩子非空的情况都要进行尝试。
2、时间复杂度
3、代码详解
class WordDictionary {
private:class Node {public:bool end;Node *childs[26];Node() : end(false) {memset(childs, 0, sizeof(childs));}};Node *root;//深度优先搜索bool pathSearch(string word, Node *root, int index) {if (index == word.size()) {return root->end;}Node *node = root;int path = 0;if (word[index] == '.') { //字符.for (int i = 0; i < 26; i++) { //所有非空的孩子都要尝试if (node->childs[i]) {bool res = pathSearch(word, node->childs[i], index + 1);if (res) return true;}}return false;} else { //字母字符path = word[index] - 'a';if (node->childs[path] == nullptr) {return false;}return pathSearch(word, node->childs[path], index + 1);}}
public:WordDictionary() {root = new Node();}void addWord(string word) {Node *node = root;int path = 0;for (int i = 0; word[i]; i++) {path = word[i] - 'a';if (node->childs[path] == nullptr) {node->childs[path] = new Node();}node = node->childs[path];}node->end = true;}bool search(string word) {return pathSearch(word, root, 0);}
};/*** Your WordDictionary object will be instantiated and called as such:* WordDictionary* obj = new WordDictionary();* obj->addWord(word);* bool param_2 = obj->search(word);*/
相关文章:

【Leetcode】211. 添加与搜索单词 - 数据结构设计
一、题目 1、题目描述 请你设计一个数据结构,支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。 实现词典类 WordDictionary : WordDictionary() 初始化词典对象void addWord(word) 将 word 添加到数据结构中,之后可以对它…...
Discuz户外旅游|旅行游记模板/Discuz!旅行社、旅游行业门户网站模板
价值328的discuz户外旅游|旅行游记模板,本模板需要配套【仁天际-PC模板管理】插件使用。 模板说明 1、模板页面宽度1200px,简洁大气,较适合户外旅行、骑行、游记、摩旅、旅游、活动等类型的论坛、频道网站; 2、所优化的页面有&…...

【重拾C语言】十一、外部数据组织——文件
目录 前言 十一、外部数据组织——文件 11.1 重新考虑户籍管理问题——文件 11.2 文件概述 11.2.1 文件分类 11.2.2 文件指针、标记及文件操作 11.3 打开、关闭文件 11.4 I/O操作 11.4.1 字符读写 11.4.2 字符串读写 11.4.3 格式化读写 11.4.4 数据块读写 11.4.5 …...
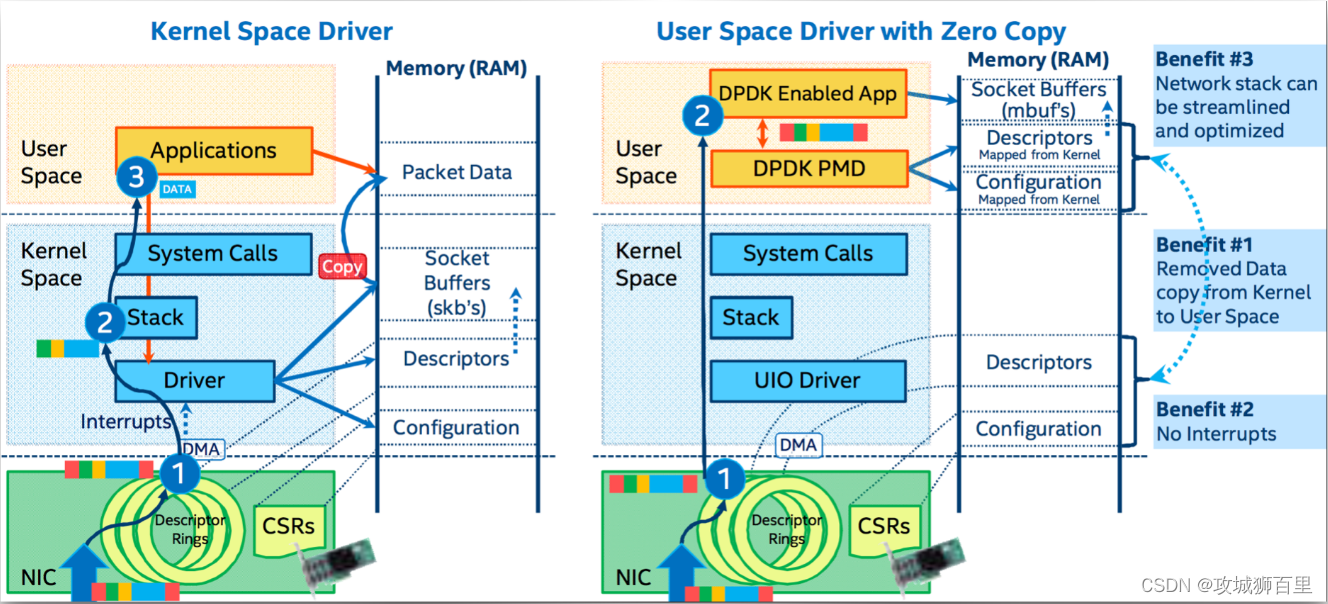
dpdk/spdk/网络协议栈/存储/网关开发/网络安全/虚拟化/ 0vS/TRex/dpvs技术专家成长体系教程
课程围绕安全,网络,存储,云原生4个维度去讲解核心技术点。 6个专栏组成:dpdk网络专栏、存储技术专栏、安全与网关开发专栏、虚拟化与云原生专栏、测试工具专栏、性能测试专栏 一、dpdk网络 dpdk基础知识 多队列网卡࿰…...

树莓派玩转openwrt软路由:5.OpenWrt防火墙配置及SSH连接
1、SSH配置 打开System -> Administration,打开SSH Access将Interface配置成unspecified。 如果选中其他的接口表示仅在给定接口上侦听,如果未指定,则在所有接口上侦听。在未指定下,所有的接口均可通过SSH访问认证。 2、防火…...

Gin:获取本机IP,获取访问IP
获取本机IP func GetLocalIP() []string {var ipStr []stringnetInterfaces, err : net.Interfaces()if err ! nil {fmt.Println("net.Interfaces error:", err.Error())return ipStr}for i : 0; i < len(netInterfaces); i {if (netInterfaces[i].Flags & ne…...

缓存降级代码结构设计
缓存降级设计思想 接前文缺陷点 本地探针应该增加计数器,多次异常再设置,避免网络波动造成误判。耦合度过高,远端缓存和本地缓存应该平行关系被设计为上下游关系了。公用的远端缓存的操作方法应该私有化,避免集成方代码误操作&…...

一文深入理解高并发服务器性能优化
我们现在已经搞定了 C10K并发连接问题 ,升级一下,如何支持千万级的并发连接?你可能说,这不可能。你说错了,现在的系统可以支持千万级的并发连接,只不过所使用的那些激进的技术,并不为人所熟悉。…...

pytorch中的归一化函数
在 PyTorch 的 nn 模块中,有一些常见的归一化函数,用于在深度学习模型中进行数据的标准化和归一化。以下是一些常见的归一化函数: nn.BatchNorm1d, nn.BatchNorm2d, nn.BatchNorm3d: 这些函数用于批量归一化 (Batch Normalization…...

【管理运筹学】第 10 章 | 排队论(1,排队论的基本概念)
文章目录 引言一、基本概念1.1 排队过程1.2 排队系统的组成和特征1.3 排队模型的分类1.4 系统指标1.5 系统状态 引言 开一点排队论的内容吧,方便做题。 排队论(Queuing Theory)也称随机服务系统理论,是为解决一系列排队问题&…...

【Express】服务端渲染(模板引擎 EJS)
EJS(Embedded JavaScript)是一款流行的模板引擎,可以用于在Express中创建动态的HTML页面。它允许在HTML模板中嵌入JavaScript代码,并且能够生成基于数据的动态内容。 下面是一个详细的讲解和示例,演示如何在Express中…...

Linux CentOS8安装gitlab_ce步骤
1 下载安装包 wget --content-disposition https://packages.gitlab.com/gitlab/gitlab-ce/packages/el/8/gitlab-ce-15.0.2-ce.0.el8.x86_64.rpm/download.rpm2 安装gitlab yum install policycoreutils-python-utilsrpm -Uvh gitlab-ce-15.0.2-ce.0.el8.x86_64.rpm3 更新配…...
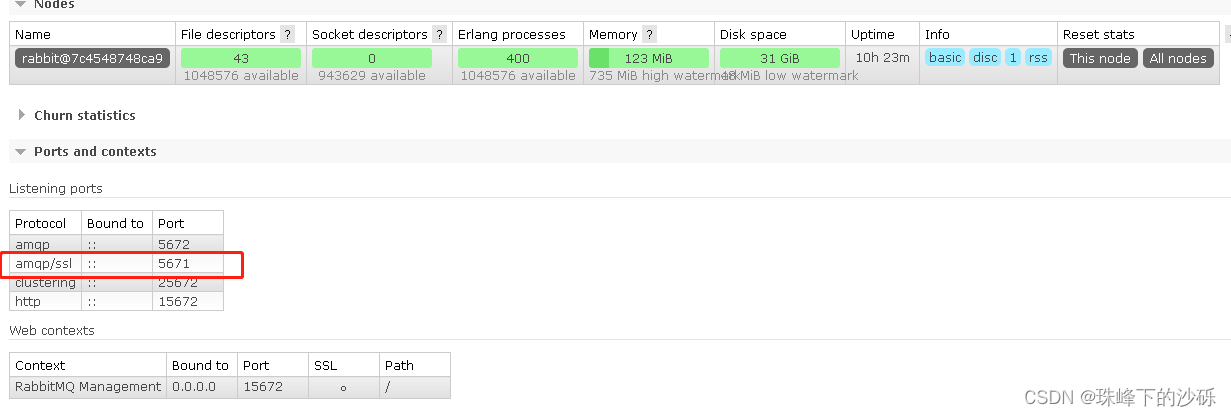
RabbitMq启用TLS
Windows环境 查看配置文件的位置 选择使用的节点 查看当前节点配置文件的配置 配置TLS 将证书放到同配置相同目录中 编辑配置文件添加TLS相关配置 [{ssl, [{versions, [tlsv1.2]}]},{rabbit, [{ssl_listeners, [5671]},{ssl_options, [{cacertfile,"C:/Users/17126…...
CakePHP 3.x/4.x反序列化RCE链
最近网上公开了cakephp一些反序列化链的细节,但是没有公开poc,并且网上关于cakephp的反序列化链比较少,于是自己跟一下 ,构造pop链。 CakePHP简介 CakePHP是一个运用了诸如ActiveRecord、Association Data Mapping、Front Contr…...

练习之C++[3]
文章目录 1.模板类2.模板声明3.string类 1.模板类 模板可以具有非类型参数,用于指定大小,可以根据指定的大小创建动态结构所以可用来创建动态增长和减小的数据结构模板运行时不检查数据类型,也不保证类型安全,相当于类型的宏替换…...

[MT8766][Android12] 修改WIFI热点默认名称、密码、IP地址以及默认开启热点
文章目录 开发平台基本信息问题描述解决方法 开发平台基本信息 芯片: MTK8766 版本: Android 12 kernel: msm-4.19 问题描述 最近做了一款没有屏幕显示的智能盒子,要想操控这款设备就只能通过adb投屏,如果默认不允许有线连接,那么要怎么实…...
【嵌入式】堆栈与单片机内存
堆栈 在片内RAM中,常常要指定一个专门的区域来存放某些特别的数据 它遵循顺序存取和后进先出(LIFO/FILO)的原则,这个RAM区叫堆栈。 其实堆栈就是单片机中的一些存储单元,这些存储单元被指定保存一些特殊信息,比如地址࿰…...

十大排序算法Java实现及时间复杂度
文章目录 十大排序算法选择排序冒泡排序插入排序希尔排序快速排序归并排序堆排序计数排序基数排序桶排序时间复杂度 参考资料 十大排序算法 选择排序 原理 从待排序的数据元素中找出最小或最大的一个元素,存放在序列的起始位置, 然后再从剩余的未排序元…...

[Go]配置国内镜像源
配置 Windows 选一个 go env -w GOPROXYhttps://goproxy.cn,direct go env -w GOPROXYhttps://mirrors.aliyun.com/goproxy,direct查看环境配置 go env...

Java知识点补充
静态方法 vs 实例方法: 静态方法(使用 static 关键字声明):属于类,不依赖于对象实例,可以通过类名直接调用。 实例方法(不使用 static 关键字声明):属于类的实例…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果