Codeforces Round 903 (Div. 3)ABCDE
Codeforces Round 903 (Div. 3)ABCDE
目录
- A. Don't Try to Count
- 题目大意
- 思路
- 核心代码
- B. Three Threadlets
- 题目大意
- 思路
- 核心代码
- C. Perfect Square
- 题目大意
- 思路
- 核心代码
- D. Divide and Equalize
- 题目大意
- 思路
- 核心代码
- E. Block Sequence
- 题目大意
- 思路
- 核心代码
A. Don’t Try to Count
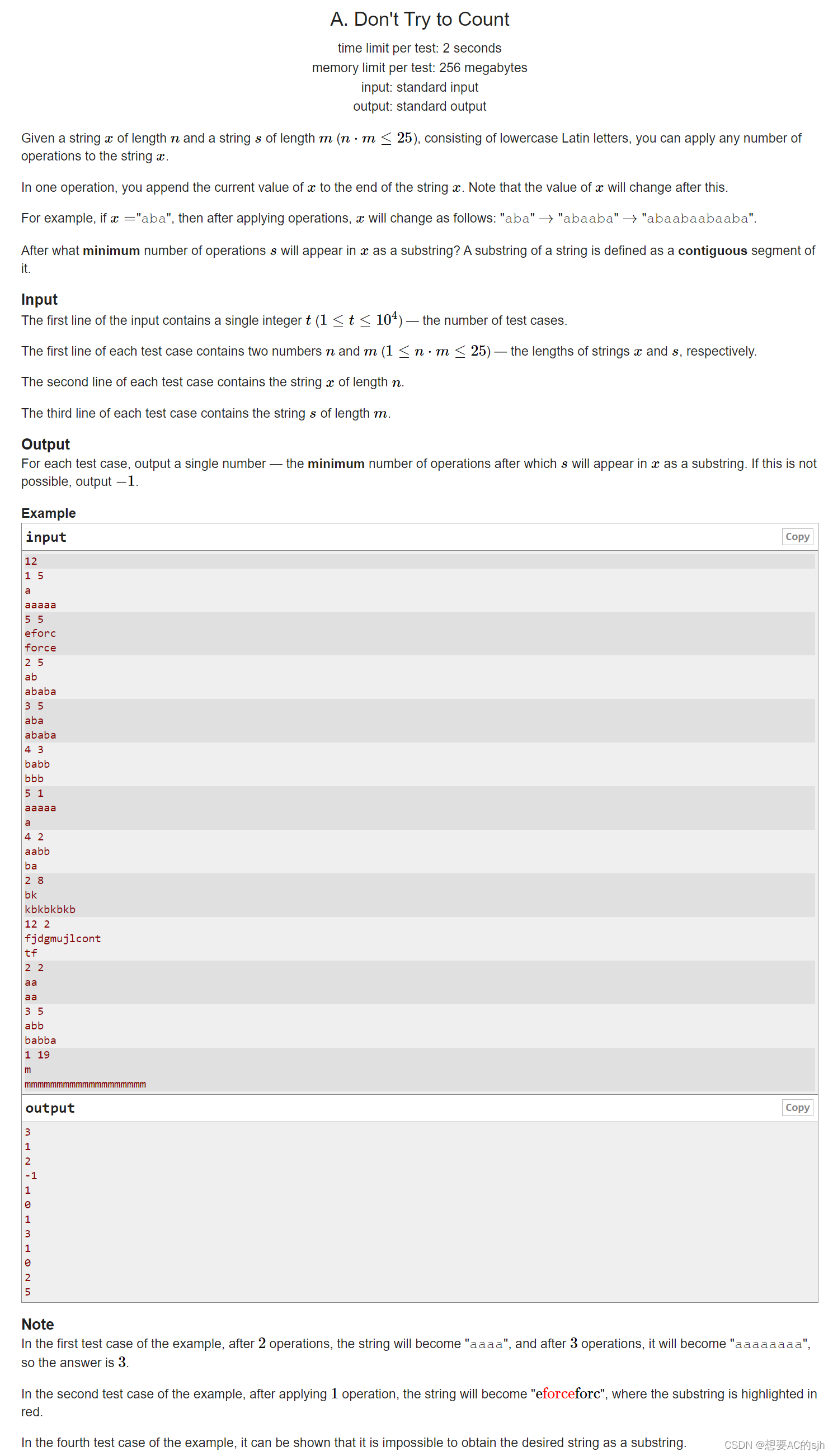
题目大意
分别给你两个字符串 s s s和 x x x,可以对 x x x进行复制操作, x = x + x x=x+x x=x+x,如果可以通过这样的操作使得 s s s字符串成为字符串 x x x的子串,询问操作的次数
思路
首先, s s s想要成为 x x x的子串,首先 x x x的长度要大于等于 s s s的长度。
其次,如果 x x x已经大于或等于 s s s的长度了,有可能会出现“abcdefg”和“gabcdef”的情况,此时我们需要再操作一次,后面无论再如何操作都无法达成题意
核心代码
void solve()
{int n,m;cin>>n>>m;string s,p;cin>>s>>p;int cnt=0;while(n<m){s=s+s;n<<=1;cnt++;}for(int i=0;i<n;++i){bool pd=1;for(int j=i;j<i+m;++j){if(s[j]!=p[j-i]){pd=0;break;}}if(pd){cout<<cnt<<endl;return ;}}s=s+s;n<<=1;cnt++;for(int i=0;i<n;++i){bool pd=1;for(int j=i;j<i+m;++j){if(s[j]!=p[j-i]){pd=0;break;}}if(pd){cout<<cnt<<endl;return ;}}cout<<-1<<endl;
}
B. Three Threadlets

题目大意
给你三个绳子长度,均为整数,每一次可以把一个绳子剪断成两个整数长度,最多减三次,询问这三个长度的绳子最后能否剪成所有的绳子长度相同
思路
最后长度相同,假设都为1,反过来进行两两相加操作可以得到能实现的比例,情况不多直接全部枚举就好,能实现的比例如下:

核心代码
void solve()
{long long a,b,c;cin>>a>>b>>c;if(a>b)swap(a,b);if(a>c)swap(a,c);if(b>c)swap(b,c);if(a*1==b*1&&b*4==c*1)cout<<"YES\n";else if(a*2==b*1&&b*3==c*2)cout<<"YES\n";else if(a*1==b*1&&b*1==c*1)cout<<"YES\n";else if(a*1==b*1&&b*3==c*1)cout<<"YES\n";else if(a*2==b*1&&b*1==c*1)cout<<"YES\n";else if(a*1==b*1&&b*2==c*1)cout<<"YES\n";else cout<<"NO\n";
}
C. Perfect Square
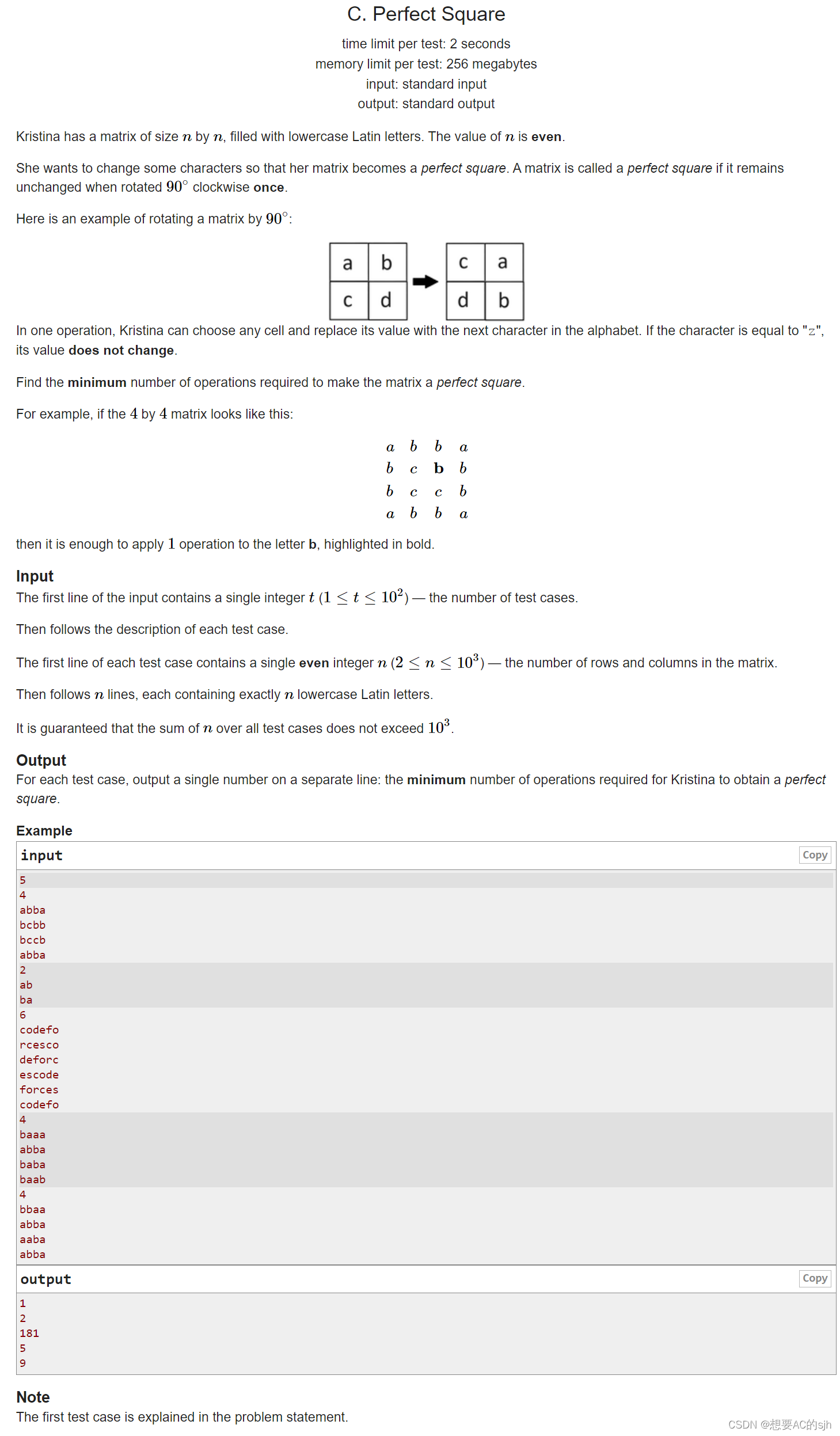
题目大意
有一个边长为偶数n的正方形字母矩阵,每一次操作可以使得一个字母向后加一,“z”之后再加就不变了,现在想要把这个方阵变成顺时针旋转90°也能和原来一样的方阵,询问最少需要操作多少次
思路
旋转之后和原来一样,假设一个字母在左上角,则可以找到右上角、左下角、右下角都会有一个对应的点,这四个点的值应该是一样的,也就是我们需要把这对应的四个点都操作为原本这四个点中的最大值,对于左上角的所有点都这样找对应关系、求操作次数即可
核心代码
void solve()
{int n;cin>>n;string s[1010];{for(int i=0;i<n;++i)cin>>s[i];}long long ans=0;for(int i=0;i<n/2;++i){for(int j=0;j<n/2;++j){int maxzhi=max(s[i][j],max(s[j][n-i-1],max(s[n-j-1][i],s[n-i-1][n-j-1])));ans+=maxzhi*4-s[i][j]-s[n-1-i][j]-s[i][n-1-j]-s[n-1-i][n-1-j];}}cout<<ans<<endl;
}
D. Divide and Equalize

题目大意
给你一个长度为 n n n的数组,每一次选取两个不同位置的数,可以把其中一个数除以它的因数,再把这个因数乘给另一个数,换句话说转化前后这两个数的乘积不变,询问最后这一个数组是否能转化为每一个数都一样
思路
最后每一个数都一样,说明所有的数的乘积后分解质因数,每一个质因数的个数都是 n n n的倍数,所以对于每一个数分解质因数最后统计每一个质因数的个数最后判断是否是 n n n的倍数即可得出答案
核心代码
int primes[N], cnt;
bool st[N];void init(int n)
{memset(st, 0, sizeof st);cnt = 0;for (int i = 2; i <= n; i ++ ){if (!st[i]) primes[cnt ++ ] = i;for (int j = 0; primes[j] * i < n; j ++ ){st[i * primes[j]] = true;if (i % primes[j] == 0) break;}}
}int zhuanghua(int a)
{int left=0,right=cnt;while(left<right){int mid=left+((right-left)/2);if(primes[mid]>a)right=mid;else if(primes[mid]==a)return mid;else left=mid+1;//debug(mid);}return left;
}
int arr[1000000];
void solve()
{int n;cin>>n;memset(arr, 0, 1000000);for(int i=0;i<n;++i){int x;scanf("%d",&x);for (int i = 2; i <= x / i; i ++ )if (x % i == 0){int s = 0;while (x % i == 0) x /= i, s ++ ;arr[zhuanghua(i)]+=s;}if (x > 1) arr[zhuanghua(x)]++;}for(int i=0;i<cnt;++i){if(arr[i]%n!=0) {cout << "NO\n";return;}}cout<<"YES\n";return ;
}int main()
{int t=1;cin>>t;init(1000000);//cout<<zhuanghua(2);while(t--){solve();}return 0;
}
E. Block Sequence

题目大意
给定一个长度n整数序列,如果一个序列具有一系列块的形式,则称为美丽,每个块都从其长度开始,即首先是块的长度,然后是其元素。在一个操作中,可以从序列中删除任何元素。使给定序列美观所需的最小操作数是多少?
思路
使用动态规划的思想,假设dp[i]为第i的位置前面所有的数字想要成为美丽序列需要几次操作
一共有两种操作,第一种是移除第i位来实现,此时需要操作的次数为dp[i-1]+1
第二种是前面有一个完整的美丽块来实现,这种只能通过前面来推出后面,假设选中第i位为开头,那么后面第 i + a i + 1 i+ai+1 i+ai+1位以前想要成为美丽序列所需要的操作就是 d p [ i + a i + 1 ] = d p [ i ] dp[i+ai+1]=dp[i] dp[i+ai+1]=dp[i]
以上两种情况保留最小值
核心代码
void solve()
{int n;cin>>n;int arr[200005]{};int dp[200005]{};for(int i=1;i<=n;++i){scanf("%d",&arr[i]);dp[i]=INT_MAX;}dp[n+1]=INT_MAX;dp[0]=-1;for(int i=1;i<=n+1;++i){dp[i]=min(dp[i-1]+1,dp[i]);if(i+arr[i]+1<=n+1)dp[i+arr[i]+1]=min(dp[i],dp[i+arr[i]+1]);}cout<<dp[n+1]<<endl;
}
相关文章:

Codeforces Round 903 (Div. 3)ABCDE
Codeforces Round 903 (Div. 3)ABCDE 目录 A. Dont Try to Count题目大意思路核心代码 B. Three Threadlets题目大意思路核心代码 C. Perfect Square题目大意思路核心代码 D. Divide and Equalize题目大意思路核心代码 E. Block Sequence题目大意思路核心代码 A. Don’t Try t…...

C# 与 C/C++ 的交互
什么是平台调用 (P/Invoke) P/Invoke 是可用于从托管代码访问非托管库中的结构、回调和函数的一种技术。 托管代码与非托管的区别 托管代码和非托管代码的主要区别是内存管理方式和对计算机资源的访问方式。托管代码通常运行在托管环境中,如 mono 或 java 虚拟机等…...
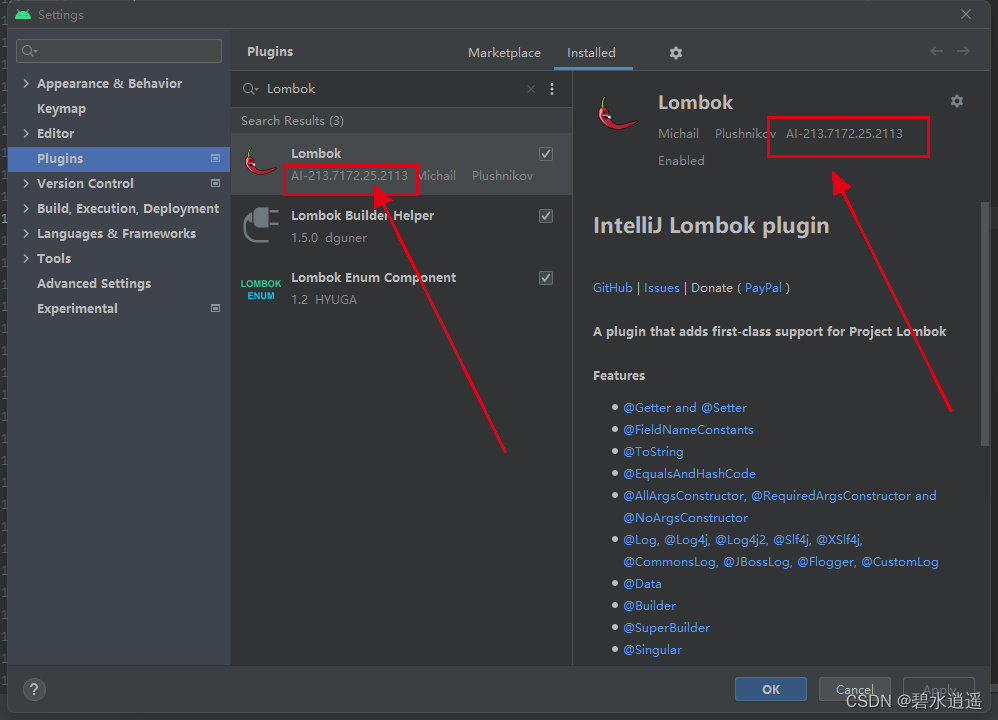
新版Android Studio搜索不到Lombok以及无法安装Lombok插件的问题
前言 在最近新版本的Android Studio中,使用插件时,在插件市场无法找到Lombox Plugin,具体表现如下图所示: 1、操作步骤: (1)打开Android Studio->Settings->Plugins,搜索Lom…...

BST二叉搜索树
文章目录 概述实现创建节点查找节点增加节点查找后驱值根据关键词删除找到树中所有小于key的节点的value 概述 二叉搜索树,它具有以下的特性,树节点具有一个key属性,不同节点之间key是不能重复的,对于任意一个节点,它…...

【Leetcode】211. 添加与搜索单词 - 数据结构设计
一、题目 1、题目描述 请你设计一个数据结构,支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。 实现词典类 WordDictionary : WordDictionary() 初始化词典对象void addWord(word) 将 word 添加到数据结构中,之后可以对它…...
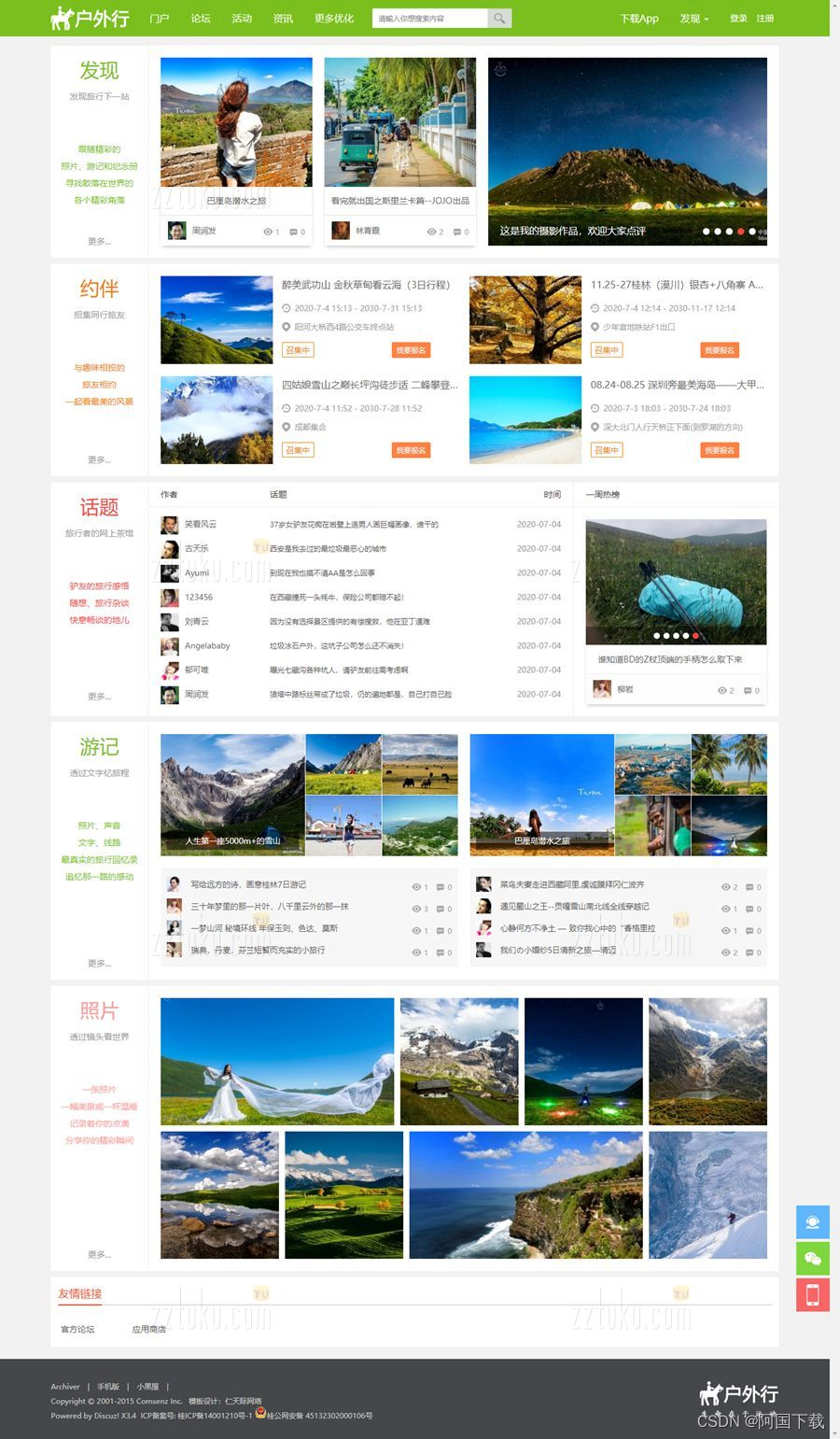
Discuz户外旅游|旅行游记模板/Discuz!旅行社、旅游行业门户网站模板
价值328的discuz户外旅游|旅行游记模板,本模板需要配套【仁天际-PC模板管理】插件使用。 模板说明 1、模板页面宽度1200px,简洁大气,较适合户外旅行、骑行、游记、摩旅、旅游、活动等类型的论坛、频道网站; 2、所优化的页面有&…...

【重拾C语言】十一、外部数据组织——文件
目录 前言 十一、外部数据组织——文件 11.1 重新考虑户籍管理问题——文件 11.2 文件概述 11.2.1 文件分类 11.2.2 文件指针、标记及文件操作 11.3 打开、关闭文件 11.4 I/O操作 11.4.1 字符读写 11.4.2 字符串读写 11.4.3 格式化读写 11.4.4 数据块读写 11.4.5 …...
dpdk/spdk/网络协议栈/存储/网关开发/网络安全/虚拟化/ 0vS/TRex/dpvs技术专家成长体系教程
课程围绕安全,网络,存储,云原生4个维度去讲解核心技术点。 6个专栏组成:dpdk网络专栏、存储技术专栏、安全与网关开发专栏、虚拟化与云原生专栏、测试工具专栏、性能测试专栏 一、dpdk网络 dpdk基础知识 多队列网卡࿰…...

树莓派玩转openwrt软路由:5.OpenWrt防火墙配置及SSH连接
1、SSH配置 打开System -> Administration,打开SSH Access将Interface配置成unspecified。 如果选中其他的接口表示仅在给定接口上侦听,如果未指定,则在所有接口上侦听。在未指定下,所有的接口均可通过SSH访问认证。 2、防火…...

Gin:获取本机IP,获取访问IP
获取本机IP func GetLocalIP() []string {var ipStr []stringnetInterfaces, err : net.Interfaces()if err ! nil {fmt.Println("net.Interfaces error:", err.Error())return ipStr}for i : 0; i < len(netInterfaces); i {if (netInterfaces[i].Flags & ne…...

缓存降级代码结构设计
缓存降级设计思想 接前文缺陷点 本地探针应该增加计数器,多次异常再设置,避免网络波动造成误判。耦合度过高,远端缓存和本地缓存应该平行关系被设计为上下游关系了。公用的远端缓存的操作方法应该私有化,避免集成方代码误操作&…...

一文深入理解高并发服务器性能优化
我们现在已经搞定了 C10K并发连接问题 ,升级一下,如何支持千万级的并发连接?你可能说,这不可能。你说错了,现在的系统可以支持千万级的并发连接,只不过所使用的那些激进的技术,并不为人所熟悉。…...

pytorch中的归一化函数
在 PyTorch 的 nn 模块中,有一些常见的归一化函数,用于在深度学习模型中进行数据的标准化和归一化。以下是一些常见的归一化函数: nn.BatchNorm1d, nn.BatchNorm2d, nn.BatchNorm3d: 这些函数用于批量归一化 (Batch Normalization…...

【管理运筹学】第 10 章 | 排队论(1,排队论的基本概念)
文章目录 引言一、基本概念1.1 排队过程1.2 排队系统的组成和特征1.3 排队模型的分类1.4 系统指标1.5 系统状态 引言 开一点排队论的内容吧,方便做题。 排队论(Queuing Theory)也称随机服务系统理论,是为解决一系列排队问题&…...

【Express】服务端渲染(模板引擎 EJS)
EJS(Embedded JavaScript)是一款流行的模板引擎,可以用于在Express中创建动态的HTML页面。它允许在HTML模板中嵌入JavaScript代码,并且能够生成基于数据的动态内容。 下面是一个详细的讲解和示例,演示如何在Express中…...

Linux CentOS8安装gitlab_ce步骤
1 下载安装包 wget --content-disposition https://packages.gitlab.com/gitlab/gitlab-ce/packages/el/8/gitlab-ce-15.0.2-ce.0.el8.x86_64.rpm/download.rpm2 安装gitlab yum install policycoreutils-python-utilsrpm -Uvh gitlab-ce-15.0.2-ce.0.el8.x86_64.rpm3 更新配…...
RabbitMq启用TLS
Windows环境 查看配置文件的位置 选择使用的节点 查看当前节点配置文件的配置 配置TLS 将证书放到同配置相同目录中 编辑配置文件添加TLS相关配置 [{ssl, [{versions, [tlsv1.2]}]},{rabbit, [{ssl_listeners, [5671]},{ssl_options, [{cacertfile,"C:/Users/17126…...
CakePHP 3.x/4.x反序列化RCE链
最近网上公开了cakephp一些反序列化链的细节,但是没有公开poc,并且网上关于cakephp的反序列化链比较少,于是自己跟一下 ,构造pop链。 CakePHP简介 CakePHP是一个运用了诸如ActiveRecord、Association Data Mapping、Front Contr…...

练习之C++[3]
文章目录 1.模板类2.模板声明3.string类 1.模板类 模板可以具有非类型参数,用于指定大小,可以根据指定的大小创建动态结构所以可用来创建动态增长和减小的数据结构模板运行时不检查数据类型,也不保证类型安全,相当于类型的宏替换…...

[MT8766][Android12] 修改WIFI热点默认名称、密码、IP地址以及默认开启热点
文章目录 开发平台基本信息问题描述解决方法 开发平台基本信息 芯片: MTK8766 版本: Android 12 kernel: msm-4.19 问题描述 最近做了一款没有屏幕显示的智能盒子,要想操控这款设备就只能通过adb投屏,如果默认不允许有线连接,那么要怎么实…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
