Leetcode---365周赛
题目列表
2873. 有序三元组中的最大值 I
2874. 有序三元组中的最大值 II
2875. 无限数组的最短子数组
2876. 有向图访问计数
一、有序三元组中的最大值I

 看一眼该题的数据范围,直接三层for循环暴力枚举,时间复杂度O(n^3),代码如下
看一眼该题的数据范围,直接三层for循环暴力枚举,时间复杂度O(n^3),代码如下
class Solution {
public:long long maximumTripletValue(vector<int>& nums) {long long ans=0;for(int i=0;i<nums.size();i++){for(int j=i+1;j<nums.size();j++){for(int k=j+1;k<nums.size();k++){ans=max(ans,1LL*(nums[i]-nums[j])*nums[k]);}}}return ans;}
};二、有序三元组的最大值II
题目同上一题,只有数据范围不同

同一个题,数据范围变大之后,再用暴力就会超时,我们要想想怎么优化时间复杂度 ?
这里有三种思路:
1.我们枚举i,看j,k怎么选?
2.我们枚举j,看i,k怎么选?
3.我们枚举k,看i,j怎么选?
假设我们选择方案一:枚举i(即先确定一个nums[ i ]),那么nums[ j ]和nums[ k ]要如何选?才能让三元组的值最大,显然nums[ j ]要选最小的,nums[ k ]选最大的,这样三元组值最大,但是还有一个条件j<k,这就很难办了, 因为我们不能确定要选择的最小值和最大值的位置关系,所以方案一不选
假设我们选择方案二:枚举j(即先确定一个nums[ j ]),那么nums[ i ]和nums[ k ]要如何选?才能让三元组的值最大,显然nums[ i ]选最大的,nums[ k ]也选最大的,这样三元组值最大,并且i<j<k,即我们选取的nums[ i ]和nums[ k ]是互不影响的,我们只要预处理出前i个元素的最大值,和后i个元素的最大值,就能在O(n)的时间复杂度内找到答案,代码如下
class Solution {
public:long long maximumTripletValue(vector<int>& nums) {int n=nums.size();long long ans=0;vector<int>pre(n+1),suf(n);pre[0]=0;for(int i=0;i<n;i++)pre[i+1]=max(pre[i],nums[i]);for(int i=n-1;i>=1;i--)suf[i-1]=max(suf[i],nums[i]);for(int j=0;j<n;j++)ans=max(ans,1LL*(pre[j]-nums[j])*suf[j]);return ans;}
};//当然这里的前缀最大值数组还可以优化掉
class Solution {
public:long long maximumTripletValue(vector<int>& nums) {int n=nums.size();long long ans=0;vector<int>suf(n);for(int i=n-1;i>=1;i--)suf[i-1]=max(suf[i],nums[i]);for(int j=1,pre=nums[0];j<n;j++){ans=max(ans,1LL*(pre-nums[j])*suf[j]);pre=max(pre,nums[j]);}return ans;}
};假设我们选择方案三:枚举k(即先确定一个nums[ k ]),那么nums[ i ]和nums[ j ]要如何选?才能让三元组的值最大,即nums[ i ] - nums[ j ]要最大,那么这不就是在遍历的过程中,维护一个前缀最大值和一个最大高度差吗,(估计有人不太能理解,我画个折线图,大家应该能好懂一些,思路和121. 买卖股票的最佳时机很相似)
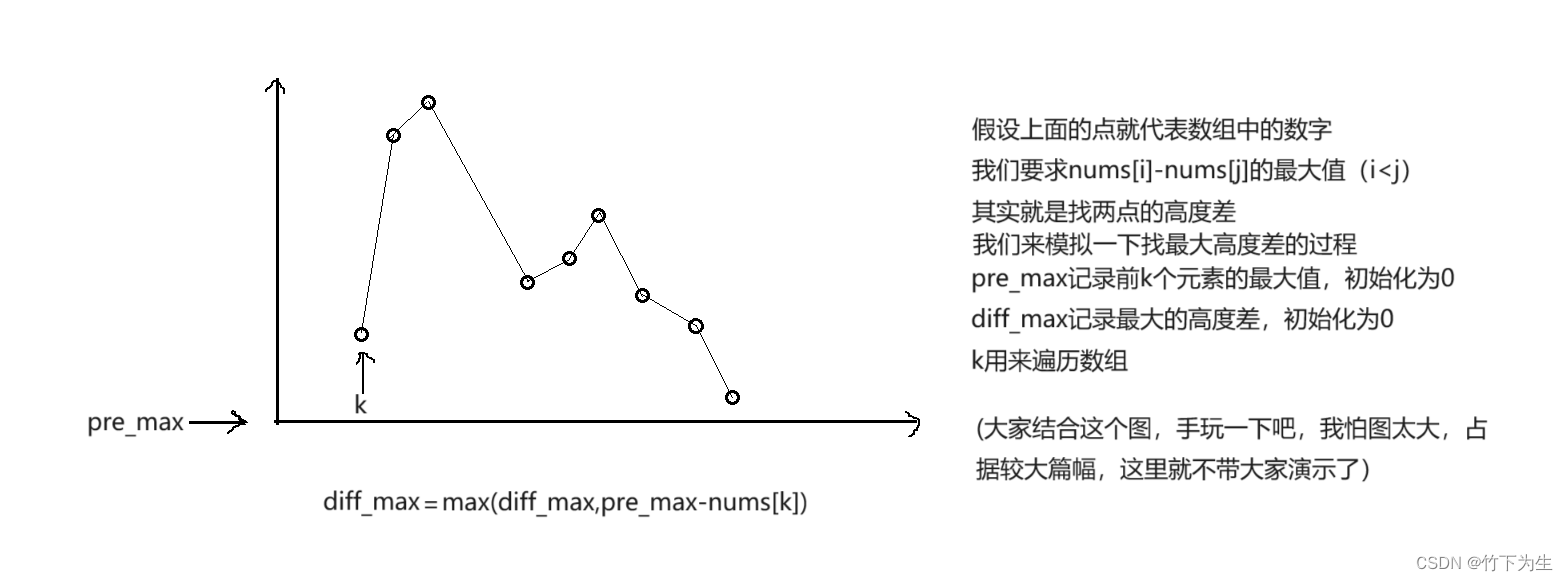
代码如下
class Solution {
public:long long maximumTripletValue(vector<int>& nums) {int n=nums.size();long long ans=0;for(int k=0,pre=0,diff=0;k<n;k++){ans=max(ans,1LL*diff*nums[k]);diff=max(diff,pre-nums[k]);pre=max(pre,nums[k]);}return ans;}
};(大家可以试着将第二题的代码放到第一题去跑一跑,对比一下两者的时间,感受一下算法的魅力)
三、无限数组的最短子数组

看到找最短的子数组的和等于target,第一个想到的就是滑动窗口,当然这题和正常的滑窗有点不同,它给的数组是个可以循环的无限长数组。
我们要弄明白两个问题:
1.我们需要一直遍历到无限远吗?不需要,我们的left端点只要在2倍的该数组里面遍历就行,因为一旦超过这个范围,后面的就又会开始循环之前遍历的结果,没有任何意义。
2.如果target>=sum(nums) ,我们的子数组还需要从0开始增加长度吗?不用,因为不论怎么枚举,子数组的长度都会有length(nums)*(target/sum(nums))的基础长度,我们只要关心target%sum(nums)这部分的最小子数组的长度就可以了,这样我们就将子数组差分成了两个部分,一个是以整个数组为单位的,一个是单独考虑的。
当然肯定有人会怀疑我们这种想法是不是太想当然了,万一这两部分不能形成一个子数组怎么办?好,这里我们就构造一个这样的子数组,我们假定找到了单独考虑的那部分子数组,然后我们继续向后延伸,由于数组是循环的,所以我们总能找到和原数组长度一样的,值相等的区间,如此循环就能构造出我们想要的最短子数组,即上面的想法正确
代码如下
class Solution {
public:typedef long long LL;int minSizeSubarray(vector<int>& nums, int target) {LL sum=accumulate(nums.begin(),nums.end(),0LL);int n=nums.size();int s=0,ans=INT_MAX;for(int left=0,right=0;right<2*n;right++){s+=nums[right%n];while(s>(target%sum)){s-=nums[left%n];left++;}if(s==(target%sum)) ans=min(ans,right-left+1);}if(ans==INT_MAX)return -1;return ans+target/sum*n;}
};四、有向图访问计数
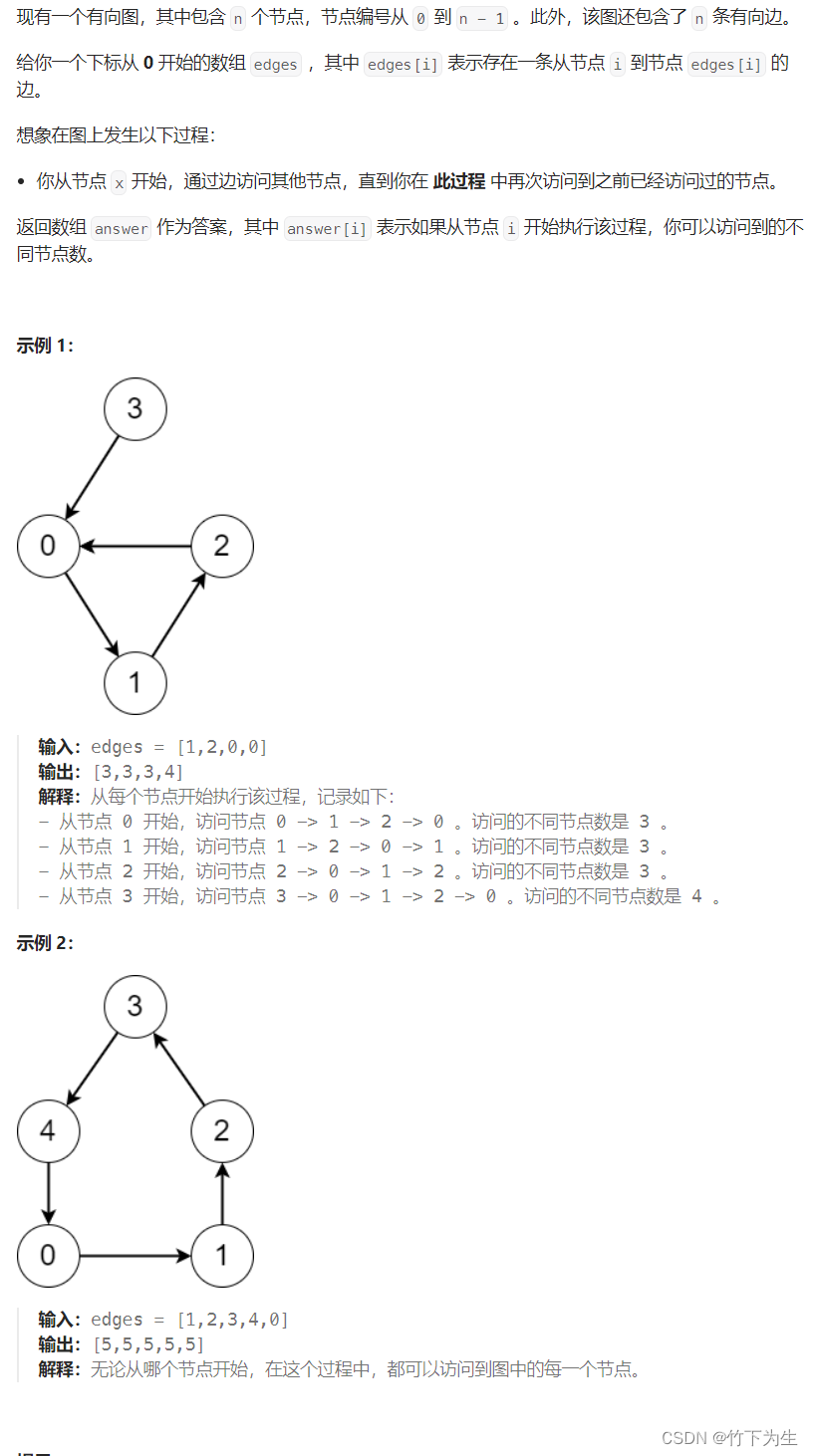
这是一个求每个结点向下能访问多少个不同结点的问题,我们需要用拓扑排序将每个环从图中拆下来单独考虑,得到换上每个结点的访问个数,然后利用返图,计算不在环上的点的访问个数,
代码如下
class Solution {
public:vector<int> countVisitedNodes(vector<int>& edges) {int n=edges.size();vector<vector<int>>g(n);//反图vector<int>deg(n);//入度for(int i=0;i<n;i++){g[edges[i]].push_back(i);deg[edges[i]]++;}//拓扑排序queue<int>q;//存放入读为0的点for(int i=0;i<n;i++){if(deg[i]==0)q.push(i);}//将不在环上的结点从图中去掉,指的是将结点的入度设置为0while(!q.empty()){int x=q.front();q.pop();if(--deg[edges[x]]==0)q.push(edges[x]);}vector<int>ans(n);//计算不在环上的点function<void(int,int)>dfs=[&](int x,int depth){ans[x]=depth;for(int y:g[x]){if(deg[y]==0){//环上的点入度为-1,这里只遍历不在环上的点dfs(y,depth+1);}}};for(int i=0;i<n;i++){if(deg[i]<=0) continue;//先计算环上的点的个数vector<int>node;for(int x=i;;x=edges[x]){node.push_back(x);deg[x]=-1;//被计算过的环上的点的入度设为-1if(edges[x]==i)break;}for(int x:node){dfs(x,node.size());}}return ans;}
};相关文章:

Leetcode---365周赛
题目列表 2873. 有序三元组中的最大值 I 2874. 有序三元组中的最大值 II 2875. 无限数组的最短子数组 2876. 有向图访问计数 一、有序三元组中的最大值I 看一眼该题的数据范围,直接三层for循环暴力枚举,时间复杂度O(n^3),代码如下 class…...

Java使用opencv实现人脸识别、人脸比对
1. opencv概述 OpenCV是一个开源的计算机视觉库,它提供了一系列丰富的图像处理和计算机视觉算法,包括图像读取、显示、滤波、特征检测、目标跟踪等功能。 opencv官网:https://opencv.org/ opencv官网文档:https://docs.opencv.or…...
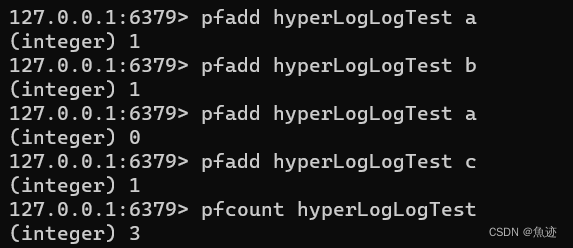
Redis HyperLogLog的使用
Redis HyperLogLog知识总结 一、简介二、使用 一、简介 Redis HyperLogLog是一种数据结构,用于高效地计算基数(集合中唯一元素的数量)。它的主要作用是用于在内存中高效地存储和计算大量数据的基数,而无需完全存储所有的数据。Hy…...

Apisix-Ingress服务发现详解
apisix Apache APISIX 是一个基于微服务 API 网关,其不仅可以处理南北向的流量,也可以处理东西向的流量即服务之间的流量。Apache APISIX 集成了控制面板和数据面,与其他 API 网关相比,Apache APISIX 的上游、路由、插件全是动态的…...

spring6-事务
文章目录 1、JdbcTemplate1.1、简介1.2、准备工作1.3、实现CURD①装配 JdbcTemplate②测试增删改功能③查询数据返回对象④查询数据返回list集合⑤查询返回单个的值 2、声明式事务概念2.1、事务基本概念①什么是事务②事务的特性 2.2、编程式事务2.3、声明式事务 3、基于注解的…...
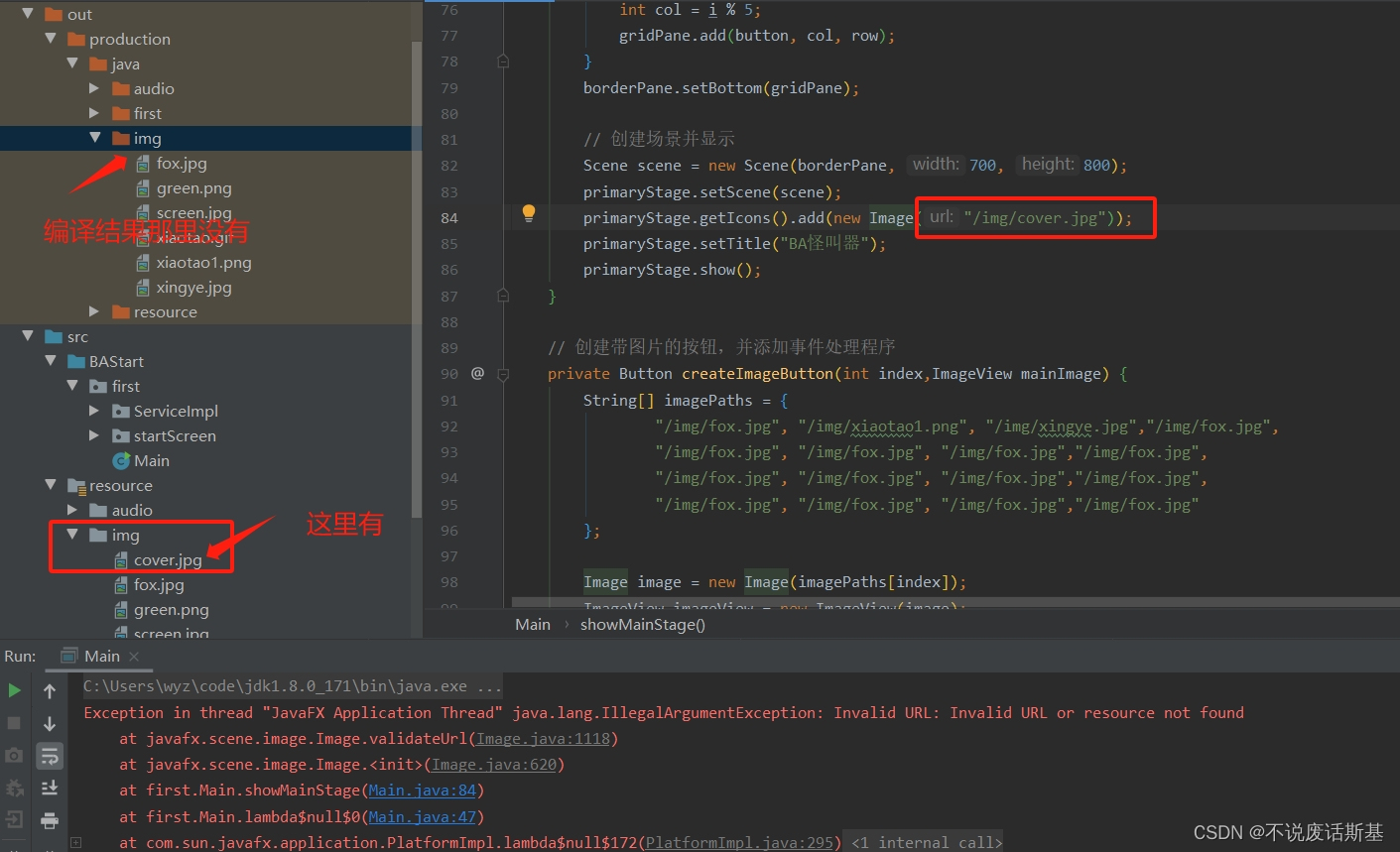
JavaFx学习问题2--音频、视频播放失败情况
文章目录 一、路径注意事项:① 用相对路径的时候别忘了前面的斜杠② uri问题 二、播放不了的问题① 获取的媒体文件路径本身就是不对的② 必须是uri③ 特殊情况 额外收获: 一、路径注意事项: 完整代码如下: import javafx.application.Application; im…...

第55节—— redux-toolkit中的createReducer——了解
一、概念 当我们使用 Redux 开发应用程序时,一个非常重要的概念就是 reducer。一个 reducer 是一个纯函数,它接受先前的状态和一个动作,然后返回一个新状态。每个动作都会引起状态的变化,从而使应用程序状态管理更加清晰和可控。…...

JUC并发编程——JUC并发编程概述及Lock锁(重点)(基于狂神说的学习笔记)
基于bilibili狂神说JUC并发编程视频所做笔记 概述 什么是JUC JUC时java.util工具包中的三个包的简称 java.util.concurrent java.util.concurrent.atomic java.util.concurrent.locks 业务:普通的线程代码中,我们常使用Runnable接口 但Runnable没有返…...

深入了解 Java 中的时间信息定义、转换、比较和操作
1. 简介 在过去的传统Java日期处理中,经常面临着一些问题。比如,java.util.Date和java.util.Calendar在表示日期和时间时存在着一些奇怪的行为,如月份从0开始计数、对日期进行格式化的方式繁琐不直观等。这些问题给开发带来了一定的困扰。 …...

2023年中国智能矿山发展历程及趋势分析:智能矿山健康有序发展[图]
智能矿山系统对矿山生产提质增效的效果已经开始显现:对不合规、有风险的行动进行及时预警,减少安全事故发生概率,避免因停产整顿产生的巨额亏损;精细化管理整个生产流程,避免过往传统粗放的流程导致的浪费,…...

acwing算法基础之基础算法--整数离散化算法
目录 1 知识点2 模板 1 知识点 整个范围很大,但存在的数据点很少。比如从 − 1 0 9 -10^9 −109到 1 0 9 10^9 109,但总共只有 1 0 6 10^6 106个数。 可以采用离散化的思想来做,即将离散的大数值映射成连续的小数值(一般是 1 , …...
基于SSM框架的安全教育平台
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...
Kafka生产者使用案例
1.生产者发送消息的过程 首先介绍一下 Kafka 生产者发送消息的过程: 1)Kafka 会将发送消息包装为 ProducerRecord 对象, ProducerRecord 对象包含了目标主题和要发送的内容,同时还可以指定键和分区。在发送 ProducerRecord 对象前,…...

EasyX图形库实现贪吃蛇游戏
⭐大家好,我是Dark Falme Masker,学习了动画制作及键盘交互之后,我们就可以开动利用图形库写一个简单的贪吃蛇小游戏,增加学习乐趣。 ⭐专栏:EasyX部分小游戏实现详细讲解 最终效果如下 首先包含头文件 #include<stdio.h> #…...
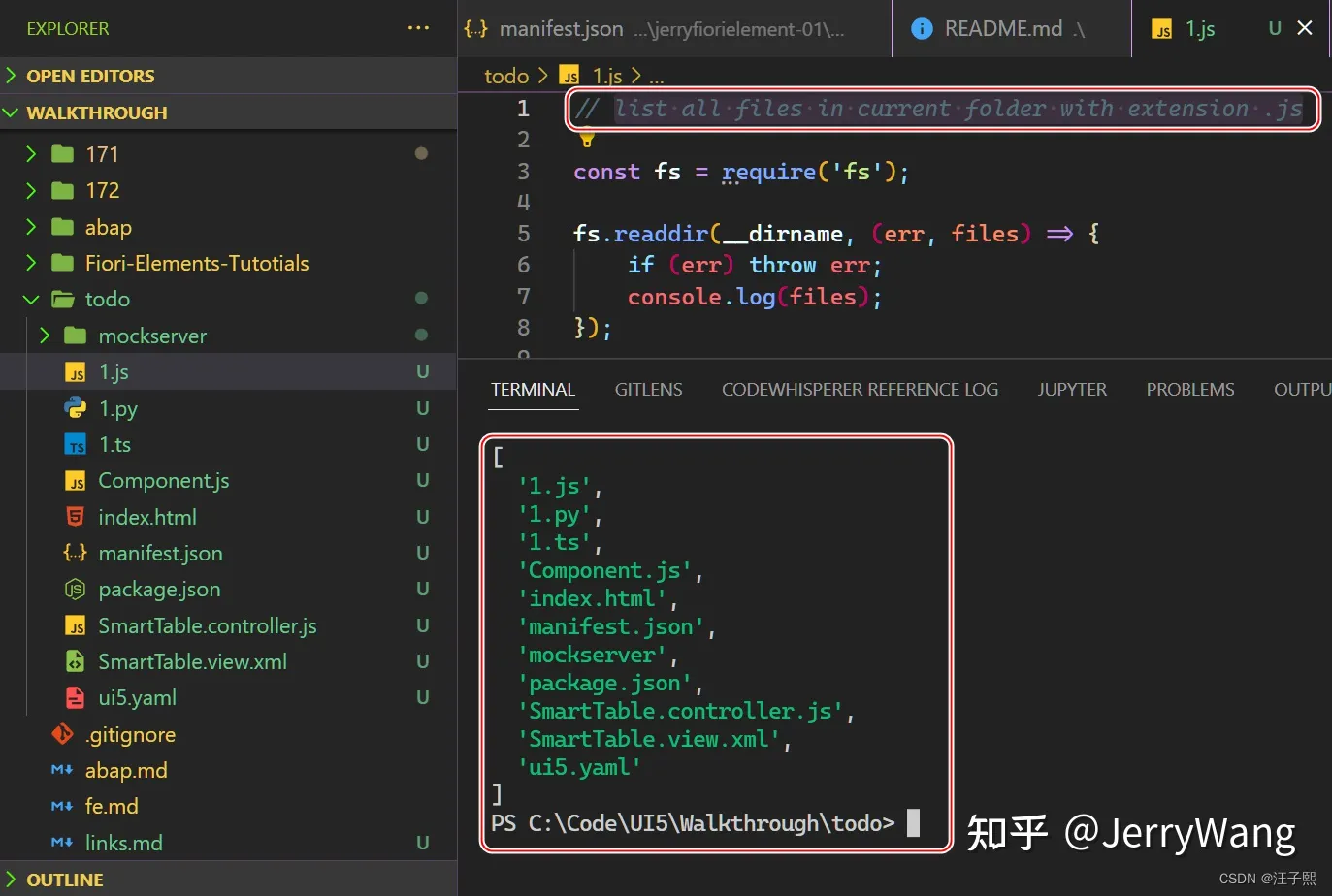
利用 Amazon CodeWhisperer 激发孩子的编程兴趣
我是一个程序员,也是一个父亲。工作之余我会经常和儿子聊他们小学信息技术课学习的 Scratch 和 Kitten 这两款图形化的少儿编程工具。 我儿子有一次指着书房里显示器上显示的 Visual Studio Code 问我,“为什么我们上课用的开发界面,和爸爸你…...
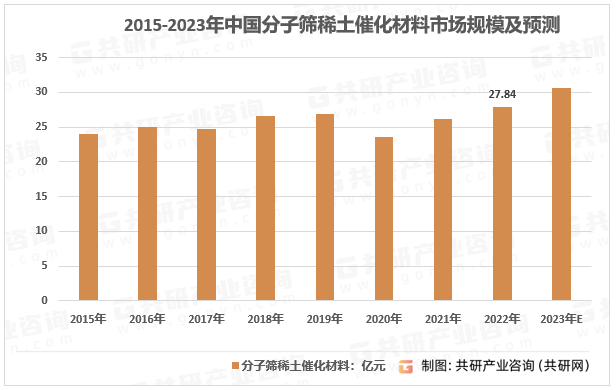
2023年中国分子筛稀土催化材料竞争格局及行业市场规模分析[图]
稀土催化材料能够起到提高催化剂热稳定性、催化剂活性、催化剂储氧能力,以及减少贵金属活性组分用量等作用,广泛应用于石油化工、汽车尾气净化、工业废气和人居环境净化、燃料电池等领域。 2015-2023年中国稀土催化材料规模及预测 资料来源:…...
vue3插件——vue-web-screen-shot——实现页面截图功能
最近在看前同事发我的vue3框架时,发现他们有个功能是要实现页面截图功能。 vue3插件——vue-web-screen-shot——实现页面截图功能 效果图如下:1.操作步骤1.1在项目中添加vvue-web-screen-shot组件1.2在项目入口文件导入组件——main.ts1.3在需要使用的页…...
简单总结Centos7安装Tomcat10.0版本
文章目录 前言JDK8安装部署Tomcat 前言 注意jdk与tomcat的兼容问题,其他的只要正确操作一般问题不大 Tomcat 是由 Apache 开发的一个 Servlet 容器,实现了对 Servlet 和 JSP 的支持,并提供了作为Web服务器的一些特有功能,如Tomca…...

ffmpeg中AVCodecContext和AVCodec的关系分析
怎么理解AVCodecContext和AVCodec的关系 AVCodecContext和AVCodec是FFmpeg库中两个相关的结构体,它们在音视频编解码中扮演着不同的角色。 AVCodecContext:是编解码器上下文结构体,用于存储音视频编解码器的参数和状态信息。它包含了进行音视…...

2023年中国门把手产量、销量及市场规模分析[图]
门把手行业是指专门从事门把手的设计、制造、销售和安装等相关业务的行业。门把手是门窗装饰硬件的一种,用于开启和关闭门窗,同时也具有装饰和美化门窗的作用。 门把手行业分类 资料来源:共研产业咨询(共研网) 随着消…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
