扩展lucas定理
前置知识:
- lucas定理
- 中国剩余定理
介绍
当正整数n,mn,mn,m很大,且质数ppp较小的时候,要求CnmC_n^mCnm对ppp取模后的值,可以用lucas定理。
但如果ppp不是质数,那该怎么办呢?如果mmm较小,则可以用扩展lucas定理。
第一步:中国剩余定理
设p=p1r1p2r2⋯pkrkp=p_1^{r_1}p_2^{r_2}\cdots p_k^{r_k}p=p1r1p2r2⋯pkrk,其中pip_ipi为质数。我们可以先求出Cnm%p1r1,Cnm%p2r2,…,Cnm%pkrkC_n^m\%p_1^{r_1},C_n^m\%p_2^{r_2},\dots,C_n^m\%p_k^{r_k}Cnm%p1r1,Cnm%p2r2,…,Cnm%pkrk的值a1,a2,…,aka_1,a_2,\dots,a_ka1,a2,…,ak。
我们把CnmC_n^mCnm看作未知数xxx,可以得到以下方程组:
{x≡a1(modp1r1)x≡a2(modp2r2)x≡a3(modp3r3)......x≡an(modpkrk)\left\{ \begin{matrix} x\equiv a_1\pmod{p_1^{r_1}}\\ x\equiv a_2\pmod{p_2^{r_2}}\\ x\equiv a_3\pmod{p_3^{r_3}}\\ ......\\ x\equiv a_n\pmod{p_k^{r_k}} \end{matrix} \right. ⎩⎨⎧x≡a1(modp1r1)x≡a2(modp2r2)x≡a3(modp3r3)......x≡an(modpkrk)
利用中国剩余定理,我们可以求出xxx,它是以ppp为周期出现的无穷多个解。而在[0,p)[0,p)[0,p)这个周期的解,就是Cnm%pC_n^m\%pCnm%p后的值。
那么a1,a2…,aka_1,a_2\dots,a_ka1,a2…,ak怎么求呢?
第二步:组合数模质数的幂
由第一步可得
a=Cnmmodpra=C_n^m\bmod p^ra=Cnmmodpr
因为Cnm=n!m!(n−m)!C_n^m=\dfrac{n!}{m!(n-m)!}Cnm=m!(n−m)!n!,我们若要求m!m!m!和(n−m)!(n-m)!(n−m)!关于prp^rpr的逆元,则要把其中所有的质因子ppp提出来,再乘回去即可。
Cnm=n!m!(n−m)!=n!pxm!py×(n−m)!pz×px−y−zC_n^m=\dfrac{n!}{m!(n-m)!}=\dfrac{\frac{n!}{p^x}}{\frac{m!}{p^y}\times \frac{(n-m)!}{p^z}}\times p^{x-y-z}Cnm=m!(n−m)!n!=pym!×pz(n−m)!pxn!×px−y−z
其中x,y,zx,y,zx,y,z分别是n!,m!,(n−m)!n!,m!,(n-m)!n!,m!,(n−m)!中质因子ppp的次数。此时m!py×(n−m)!pz\dfrac{m!}{p^y}\times \dfrac{(n-m)!}{p^z}pym!×pz(n−m)!与prp^rpr互质,可以直接求逆元。因为CnmC_n^mCnm为整数,所以x−y−z≥0x-y-z\geq 0x−y−z≥0,px−y−zp^{x-y-z}px−y−z可以用快速幂来求。
第三步:阶乘除去质因子后模质数幂
接下来的问题就是计算以下式子
n!ptmodpk\dfrac{n!}{p^t}\bmod p^kptn!modpk
我们呢先考虑如如何计算n!modpkn!\bmod p^kn!modpk。举个例子:n=22,p=3,k=2n=22,p=3,k=2n=22,p=3,k=2
22!=1×2×3×4×5×6×7×8×9×10×11×12×13×14×15×16×17×18×19×20×21×2222!=1\times 2\times 3\times 4\times 5\times 6\times 7\times 8\times 9\times 10\times 11\times 12\times 13\times 14\times 15\times 16\times 17\times 18\times 19\times 20\times 21\times 2222!=1×2×3×4×5×6×7×8×9×10×11×12×13×14×15×16×17×18×19×20×21×22
把其中333的倍数提出来,得到
22!=(3×6×9×12×15×18×21)×(1×2×4×5×7×8×10×11×13×14×16×17×19×20×22)22!=(3\times 6\times 9\times 12\times 15\times 18\times 21)\times (1\times 2\times 4\times 5\times 7\times 8\times 10\times 11\times 13\times 14\times 16\times 17\times 19\times 20\times 22)22!=(3×6×9×12×15×18×21)×(1×2×4×5×7×8×10×11×13×14×16×17×19×20×22)
=37×(1×2×3×4×5×6×7)×(1×2×4×5×7×8×10×11×13×14×16×17×19×20×22)\qquad =3^7\times (1\times 2\times 3\times 4\times 5\times 6\times 7)\times (1\times 2\times 4\times 5\times 7\times 8\times 10\times 11\times 13\times 14\times 16\times 17\times 19\times 20\times 22)=37×(1×2×3×4×5×6×7)×(1×2×4×5×7×8×10×11×13×14×16×17×19×20×22)
其中373^737即为pkp^kpk,就是需要被提出的部分。
对于7!7!7!,即为⌊np⌋!\lfloor \dfrac np\rfloor!⌊pn⌋!,可以递归来求。
对于后面的部分,我们发现
1×2×4×5×7×8≡10×11×13×14×16×17(modpk)1\times 2\times 4\times 5\times 7\times 8\equiv 10\times 11\times 13\times 14\times 16\times 17\pmod{p^k}1×2×4×5×7×8≡10×11×13×14×16×17(modpk)
我们发现1×2×4×5×7×81\times 2\times 4\times 5\times 7\times 81×2×4×5×7×8在整个式子中会出现⌊npk⌋\lfloor\dfrac{n}{p^k}\rfloor⌊pkn⌋次,因此,我们可以先计算在pkp^kpk以内的部分,然后再求其⌊npk⌋\lfloor\dfrac{n}{p^k}\rfloor⌊pkn⌋次幂。不要忘了乘上最后多出的一部分。
1×2×4×5×7×8×10×11×13×14×16×17×19×20×22≡(1×2×4×5×7×8)3×19×20×22(modpk)1\times 2\times 4\times 5\times 7\times 8\times 10\times 11\times 13\times 14\times 16\times 17\times 19\times 20\times 22\equiv (1\times 2\times 4\times 5\times 7\times 8)^3\times 19\times 20\times 22\pmod{p^k}1×2×4×5×7×8×10×11×13×14×16×17×19×20×22≡(1×2×4×5×7×8)3×19×20×22(modpk)
也就是说,对于以下式子
=37×(1×2×3×4×5×6×7)×(1×2×4×5×7×8×10×11×13×14×16×17×19×20×22)\qquad =3^7\times (1\times 2\times 3\times 4\times 5\times 6\times 7)\times (1\times 2\times 4\times 5\times 7\times 8\times 10\times 11\times 13\times 14\times 16\times 17\times 19\times 20\times 22)=37×(1×2×3×4×5×6×7)×(1×2×4×5×7×8×10×11×13×14×16×17×19×20×22)
373^737是要提出的,不用计算。第二部分可以递归计算。第三部分可以O(pk)O(p^k)O(pk)得出。
总结
扩展lucas定理与lucas定理在实现上并没有太大关联,只是解决的问题比较类似。扩展lucas定理的时间复杂度大概在O(p+log2n)O(p+\log^2 n)O(p+log2n)。当然,这是最坏的时间复杂度,一般的时间复杂度远远低于此。如果ppp的质因子比较多且都比较小,则时间复杂度会降低很多。
例题
P4720 【模板】扩展卢卡斯定理
code
#include<bits/stdc++.h>
using namespace std;
int tot=0;
long long mod,x,y,ans=0,a[105],r[105];
long long mi(long long t,long long v){if(v==0) return 1;long long re=mi(t,v/2);re=re*re%mod;if(v&1) re=re*t%mod;return re;
}
void exgcd(long long c,long long d){if(d==0){x=1;y=0;return;}exgcd(d,c%d);long long t=x;x=y;y=t-c/d*y;
}
long long gt(long long v,long long p,long long q){if(!v) return 1;long long re=1;for(int i=1;i<=q;i++){if(i%p) re=re*i%q;}re=mi(re,v/q)%q;for(int i=1;i<=v%q;i++){if(i%p) re=re*i%q;}return re*gt(v/p,p,q)%q;
}//第三步
long long C(long long v1,long long v2,long long p,long long q){if(v1<v2) return 0;long long f1=gt(v1,p,q),f2=gt(v2,p,q),f3=gt(v1-v2,p,q),vt=0;for(long long i=p;i<=v1;i*=p) vt+=v1/i;for(long long i=p;i<=v2;i*=p) vt-=v2/i;for(long long i=p;i<=v1-v2;i*=p) vt-=(v1-v2)/i;return mi(p,vt)%q*f1%q*(mi(f2,q-q/p-1)%q)%q*(mi(f3,q-q/p-1)%q)%q;
}//第二步
int main()
{long long n,m,v;scanf("%lld%lld%lld",&n,&m,&mod);v=mod;for(int i=2;i*i<=v;i++){if(v%i==0){r[++tot]=1;while(v%i==0){r[tot]*=i;v/=i;}a[tot]=C(n,m,i,r[tot]);}}if(v>1){r[++tot]=v;a[tot]=C(n,m,v,v);}v=mod;for(int i=1;i<=tot;i++){exgcd(v/r[i],r[i]);x=(x%r[i]+r[i])%r[i];ans=(ans+v/r[i]*a[i]*x%v)%v;}//第一步printf("%lld",ans);return 0;
}
相关文章:

扩展lucas定理
前置知识: lucas定理中国剩余定理 介绍 当正整数n,mn,mn,m很大,且质数ppp较小的时候,要求CnmC_n^mCnm对ppp取模后的值,可以用lucas定理。 但如果ppp不是质数,那该怎么办呢?如果mmm较小,则…...
医疗影像工具LEADTOOLS 入门教程: 从 PDF 中提取附件 - 控制台 C#
LEADTOOLS 是一个综合工具包的集合,用于将识别、文档、医疗、成像和多媒体技术整合到桌面、服务器、平板电脑、网络和移动解决方案中,是一项企业级文档自动化解决方案,有捕捉,OCR,OMR,表单识别和处理&#…...
【LVGL】学习笔记--(1)Keil中嵌入式系统移植LVGL
一 LVGL简介最近emwin用的比较烦躁,同时被LVGL酷炫的界面吸引到了,所以准备换用LVGL试试水。LVGL(轻量级和通用图形库)是一个免费和开源的图形库,它提供了创建嵌入式GUI所需的一切,具有易于使用的图形元素,美丽的视觉效…...
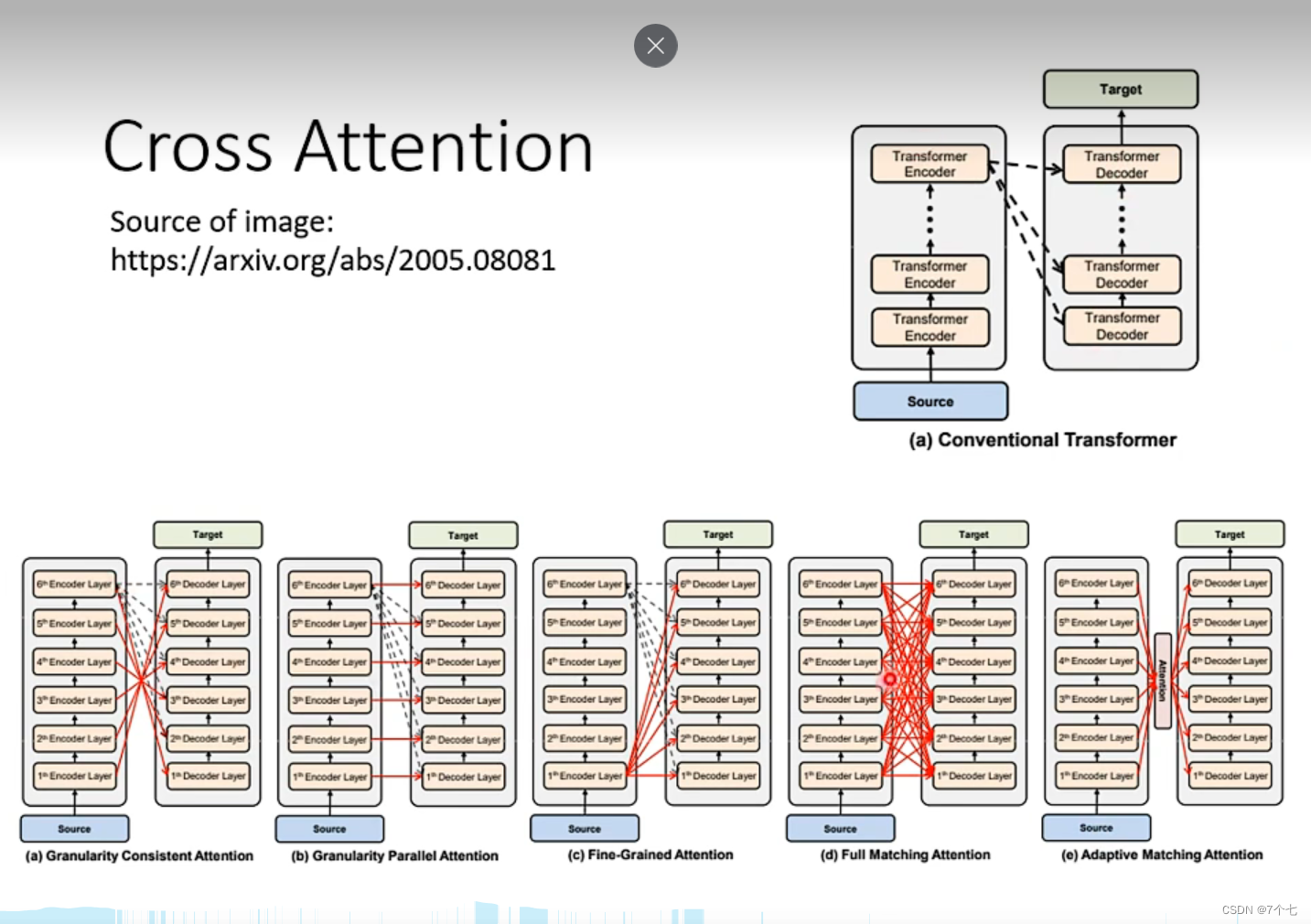
Transformer学习笔记
Transformer学习笔记1. 参考2. 模型图3.encoder部分3.1 Positional Encoding3.2 Muti-Head Attention3.3 ADD--残差连接3.4 Norm标准化3.5 单个Transformer Encoder流程图4.decoder部分4.1 mask Muti-Head Attention4.2 Muti-Head Attention5 多个Transformer Encoder和多个Tra…...
vue-cli引入wangEditor、Element,封装可上传附件的富文本编辑器组件(附源代码直接应用,菜单可调整)
关于Element安装引入,请参考我的另一篇文章:vue-cli引入Element Plus(element-ui),修改主题变量,定义全局样式_shawxlee的博客-CSDN博客_chalk variables 1、安装wangeditor npm i wangeditor --savewangE…...

移动办公时代,数智化平台如何赋能企业管理升级?
在传统的办公模式下,企业组织办公不仅时效低,周期长、成本高,且各办公系统相互独立。随着社会经济的发展,人们的工作生活变得多样化,对于办公的需求也越来越多,存在明显弊端的传统办公模式已不能满足企业对…...

2023“拼夕夕”为什么可以凭借简单的拼团做这么大?
2023“拼夕夕”为什么可以凭借简单的拼团做这么大? 2023-02-24 梦龙 大家好,我是你们熟悉而又陌生的好朋友梦龙,一个创业期的年轻人 大家都知道,拼夕夕背后的商业模式是拼团,但是大家知道为什么简单的拼团可以让拼夕…...
sqlmap工具
sqlmap Sqlmap是一个开源的渗透测试工具,可以用来自动化的检测,利用SQL注入漏洞,获取数据库服务器的权限。目前支持的数据库有MySQL、Oracle、PostgreSQL、Microsoft SQL Server、Microsoft Access等大多数据库 Sqlmap采用了以下5种独特的SQ…...
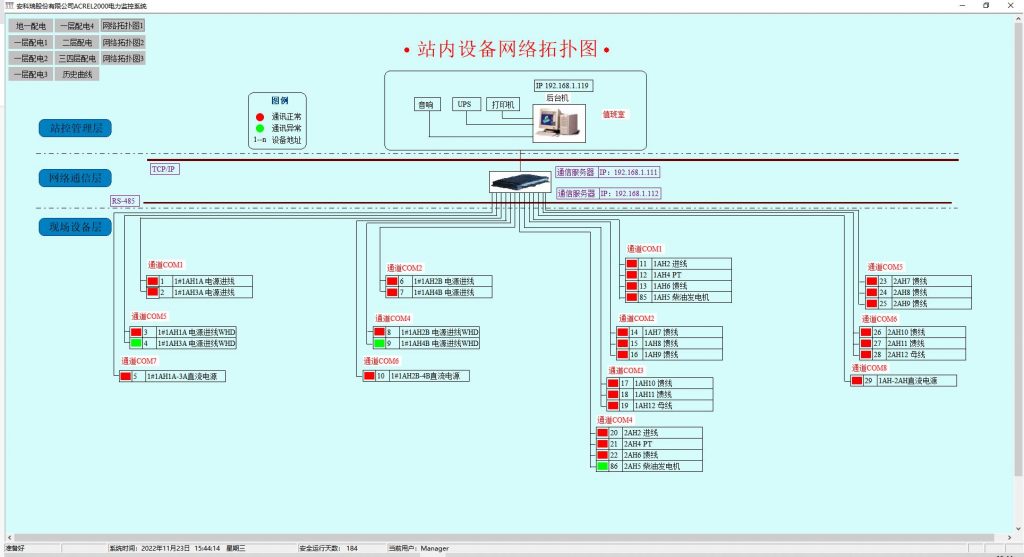
高/低压供配电系统设计——安科瑞变电站电力监控系统的应用
摘 要:在电力系统的运行过程中,变电站作为整个电力系统的核心,在保证电力系统可靠的运行方面起着至关重要的作用,基于此需对变电站监控系统的特点进行分析,结合变电站监控系统的功能需求,对变电站电力监控系…...
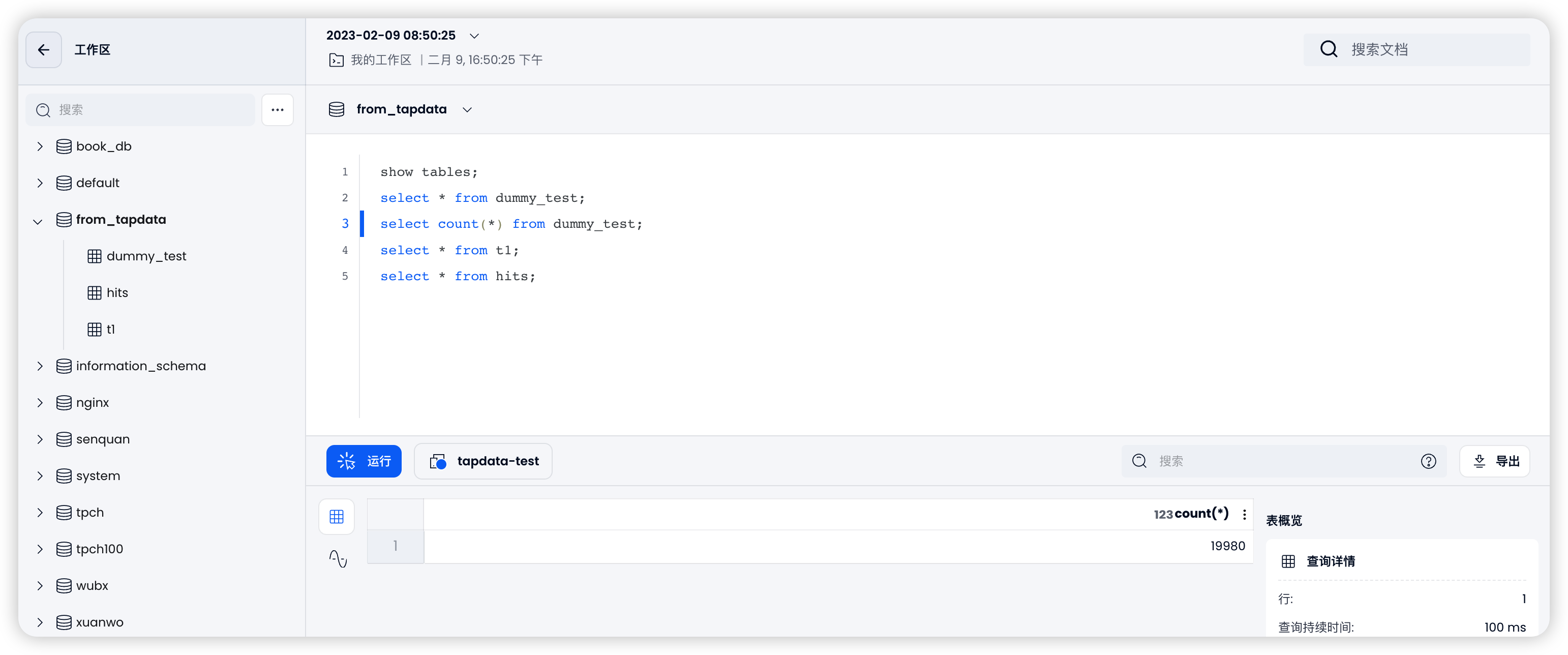
Tapdata 和 Databend 数仓数据同步实战
作者:韩山杰https://github.com/hantmacDatabend Cloud 研发工程师基础架构在云计算时代也发生着翻天地覆的变化,对于业务的支持变成了如何能利用好云资源实现降本增效,同时更好的支撑业务也成为新时代技术人员的挑战。 本篇文章通过…...
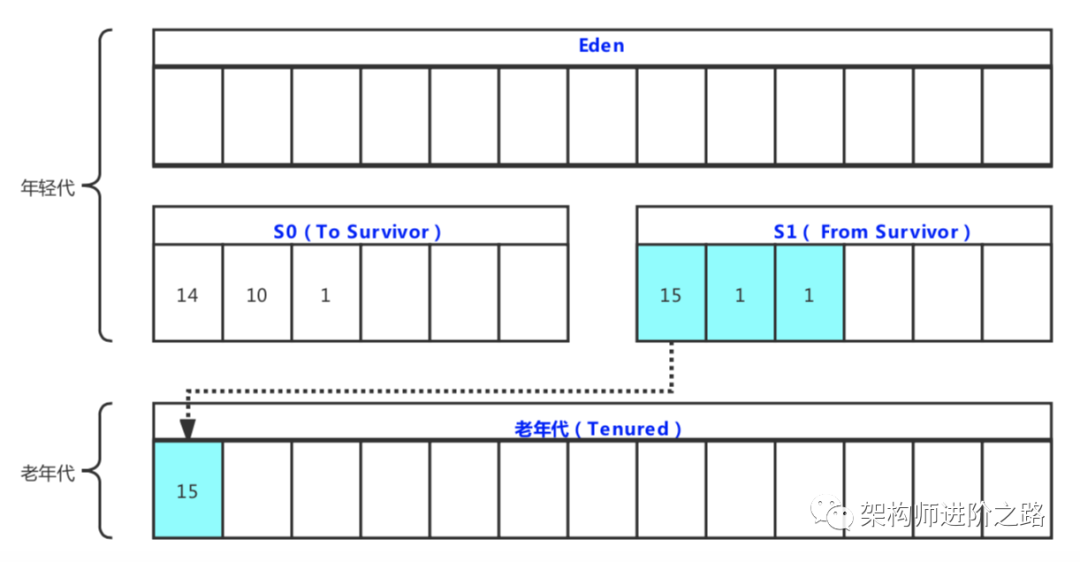
单核CPU, 1G内存,也能做JVM调优吗?
最近,笔者的技术群里有人问了一个有趣的技术话题:单核CPU, 1G内存的超低配机器,怎么做JVM调优?这实际上是两个问题。单核CPU的超低配机器,怎么充分利用CPU?单核CPU, 1G内存的超低配机器,怎么做J…...

《计算机应用研究》投稿经历和时间节点
记录四川计算机研究院《计算机应用研究》期刊投稿经历和时间节点。 日期状态周期2022.11.09上传稿件当天显示编辑部已接收稿件,开始初审2022.11.09 – 2022.11.15初审6天2022.11.15 – 2022.12.21外审36天2022.12.21收到退修意见(邮件形式)编…...
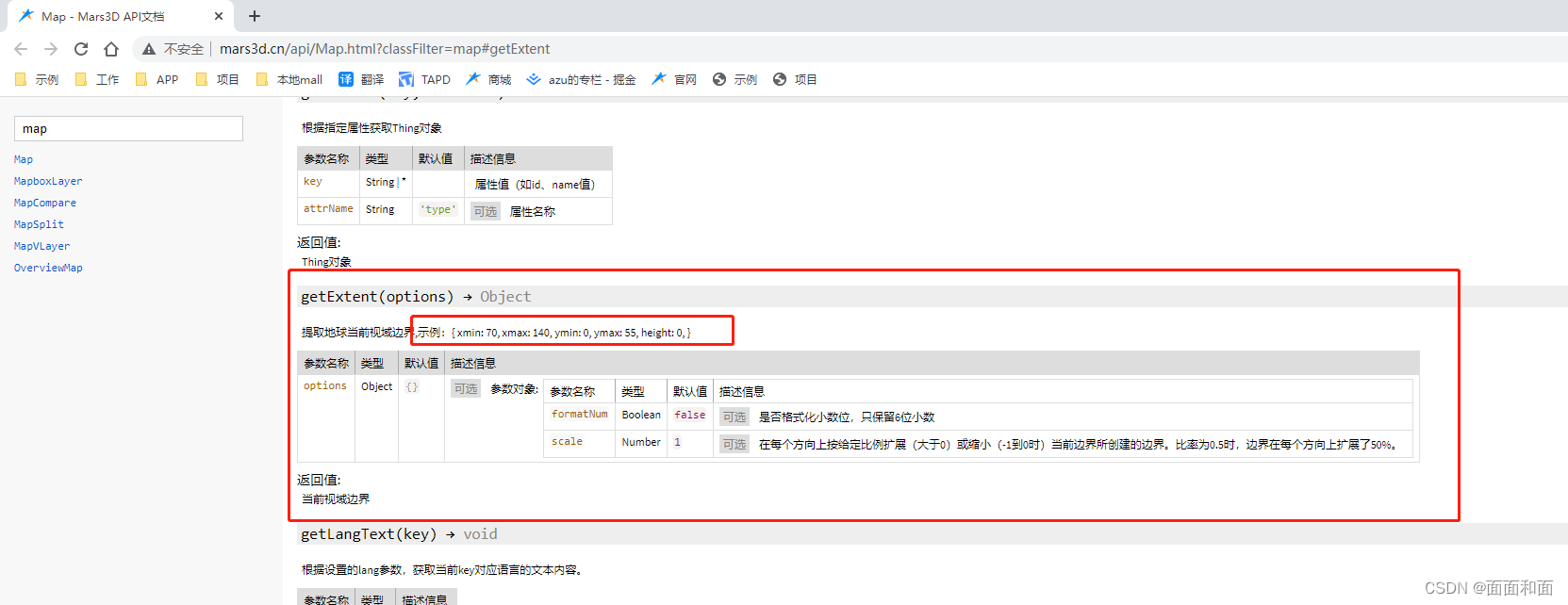
mars3d获取视窗的范围
期望效果 :1.我现在想获取到当前视窗的地图范围,请问有什么⽅法可以拿到吗 2.⽐如当前视窗地图范围的边界点,每个边界点的经纬度 回复:1.mars3d的API⽂档中有相关的⽅法 2.具体使⽤可以参考⽂档地址:http://mars3d.cn/api/Map.htm…...
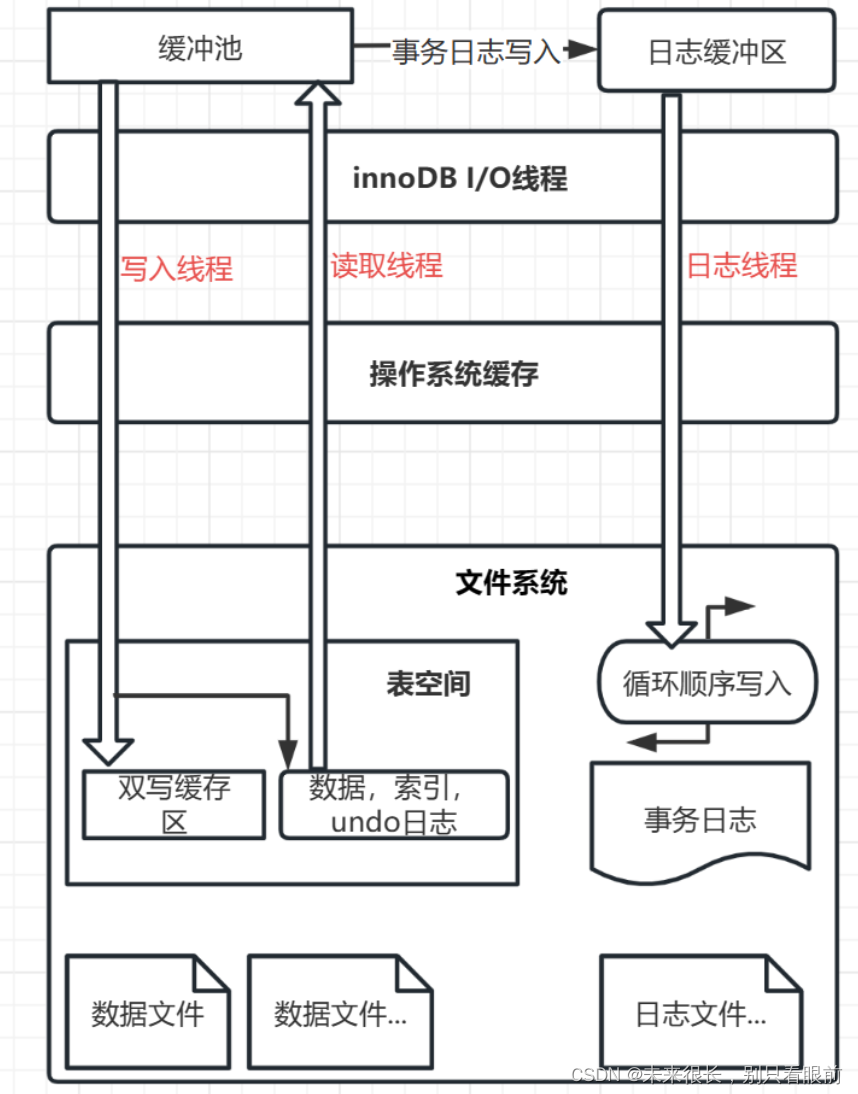
《高性能MySQL》读书笔记(上)
目录 MySQL的架构 MySQL中的锁 MySQL中的事务 事务特性 隔离级别 事务日志 多版本并发控制MVCC 影响MySQL性能的物理因素 InnoDB缓冲池 MySQL常用的数据类型以及优化 字符串类型 日期和时间类型 数据标识符 MySQL的架构 默认情况下,每个客户端连接都…...

05-代理模式
代理模式 代理模式使用代理对象来代替真实对象的访问,在不修改原有对象的前提下,提供额外的操作,扩展目标对象的功能。代理模式分为静态代理和动态代理。 静态代理 手动为目标对象中的方法进行增强,通过实现相同接口重写方法进…...

RocketMQ源码分析之消费队列、Index索引文件存储结构与存储机制-上篇
RocketMQ 存储基础回顾: 源码分析RocketMQ之CommitLog消息存储机制 本文主要从源码的角度分析 Rocketmq 消费队列 ConsumeQueue 物理文件的构建与存储结构,同时分析 RocketMQ 索引文件IndexFile 文件的存储原理、存储格式以及检索方式。RocketMQ 的存储…...
基于Java的浏览器的设计与实现毕业设计
技术:Java等摘要:当今世界是一个以计算机网络为核心的信息时代,互联网为人们快速获取、发布和传递信息提供了便捷,而浏览器作为互联网上查找信息的重要工具,给人们提供了巨大而又宝贵的信息财富,受到了大家…...
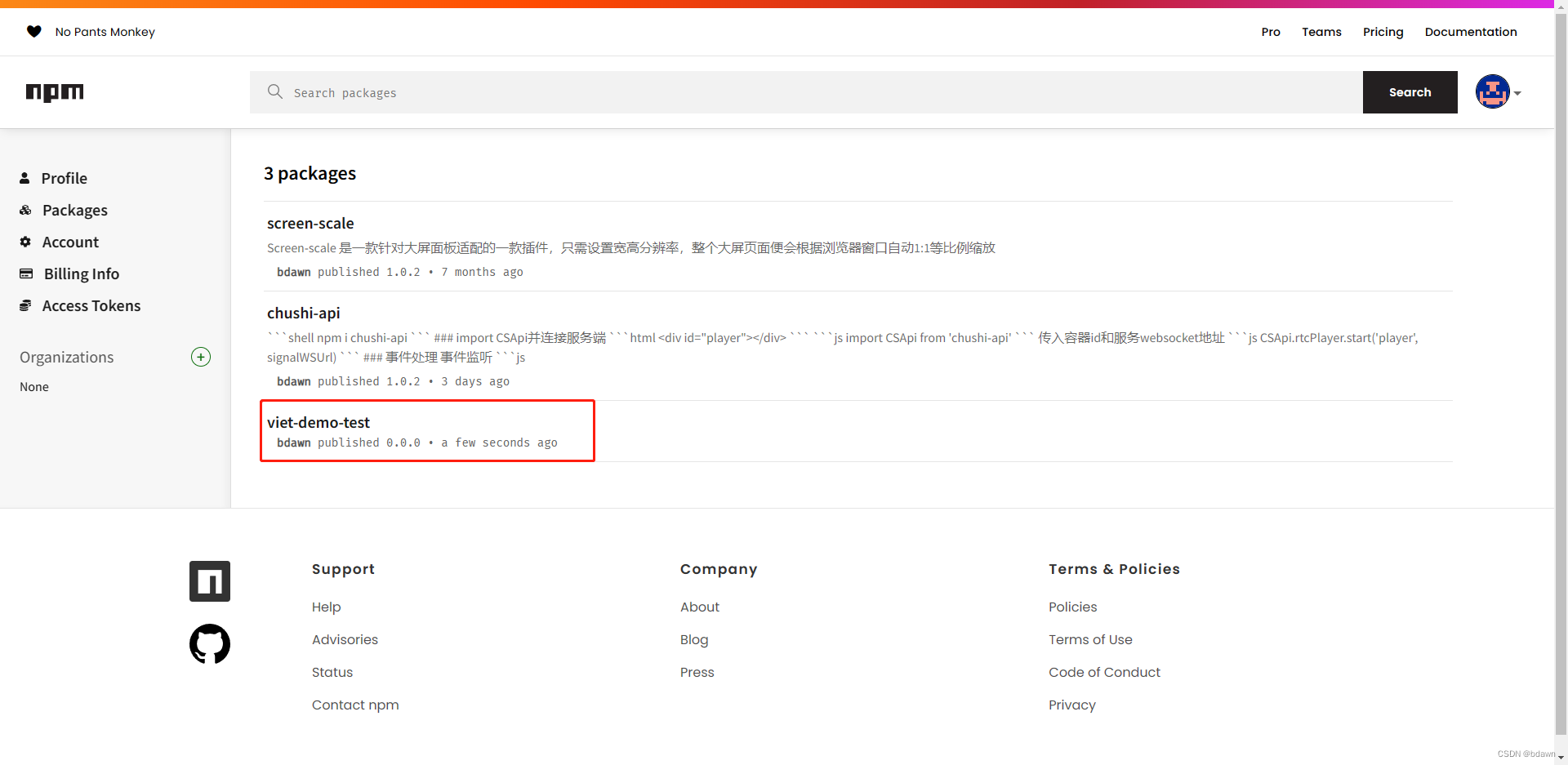
手把手教你使用vite打包自己的js代码包并推送到npm
准备 要有npm账号,没有的铁子去npm官网注册一个,又不要钱。 使用vite创建项目 一行代码搞定 npm create vite viet-demo框架选择Others 模板选择library 选择ts 这样项目就创建完了 这个项目默认有一个函数,用来记录按钮的点击次数并…...

Tomcat源码分析-关于tomcat热加载的一些思考
在前面的文章中,我们分析了 tomcat 类加载器的相关源码,也了解了 tomcat 支持类的热加载,意味着 tomcat 要涉及类的重复卸装/装载过程,这个过程是很敏感的,一旦处理不当,可能会引起内存泄露 卸载类 我们知…...
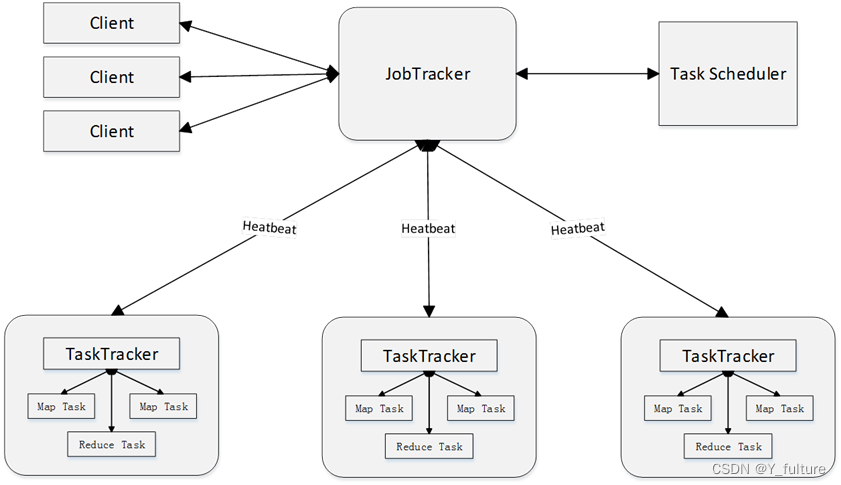
DataWhale 大数据处理技术组队学习task4
五、分布式并行编程模型MapReduce 1. 概述 1.1 分布式并行编程 背景:摩尔定律已经开始逐渐失效,提升数据处理计算能力刻不容缓。传统的程序开发与分布式并行编程 传统的程序开发:以单指令、单数据流的方式顺序执行,虽然这种方式…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...
