了解油封对汽车安全的影响?
油封也称为轴封或径向轴封,是车辆发动机、变速箱和其他各种机械系统中的重要部件。它们的主要功能是阻止重要发动机部件的液体(例如油或冷却剂)泄漏,同时防止污染物进入。这些看似简单的任务,但对汽车的安全性和可靠性有着深远的影响。
油封较重要的功能之一是保持发动机润滑。润滑良好的发动机运转平稳、高效,减少运动部件的摩擦和磨损。如果油封功能不正常,发动机的润滑系统可能会发生故障,从而导致摩擦、热量增加和潜在的发动机损坏。这反过来会导致发动机故障并影响车辆驾驶的安全性。道路上发动机突然故障可能会导致事故,尤其是在高速行驶时。
传动系统是油封在确保车辆安全方面发挥着至关重要作用的另一个领域。变速箱中的油封有助于保持必要的液位并防止污染,从而确保平稳换档和较佳性能。变速箱系统故障可能会导致齿轮打滑、换档不稳定以及车辆失控。变速箱油封的任何问题都会影响驾驶员有效控制汽车的能力,从而导致危险情况。
制动系统是任何车辆的主要安全功能,其可靠性至关重要。油封用于制动系统的各个部件,以防止液体泄漏,例如轮缸和主缸。如果制动系统的油封失效,可能会导致制动力丧失,从而可能导致事故和伤害。
除了保持发动机、变速箱和制动系统的完整性之外,油封还可以防止有害液体泄漏到道路上。油、冷却剂或液压油泄漏可能会造成危险的驾驶条件,降低牵引力并增加发生事故的风险。正常工作的油封有助于容纳这些液体,通过减少路面打滑的机会来促进道路安全。
虽然油封可能不是较受关注的车辆部件,但它们对汽车安全的影响不容低估。它们通过防止泄漏、确保适当润滑并提高车辆的可靠性,在确保汽车安全方面发挥着关键作用。
相关文章:

了解油封对汽车安全的影响?
油封也称为轴封或径向轴封,是车辆发动机、变速箱和其他各种机械系统中的重要部件。它们的主要功能是阻止重要发动机部件的液体(例如油或冷却剂)泄漏,同时防止污染物进入。这些看似简单的任务,但对汽车的安全性和可靠性有着深远的影响。 油封…...

创邻科技Galaxybase—激活数据要素的核心引擎
10月11日下午,创邻科技创始人张晨博士受杭州电子科技大学邀请,前往杭电校园开展交流分享。交流会中,张晨博士为现场的师生带来一场题为《图数据库——激活数据要素的新基建》的精彩分享,探讨数字经济时代底层技术的创新价值与图技…...
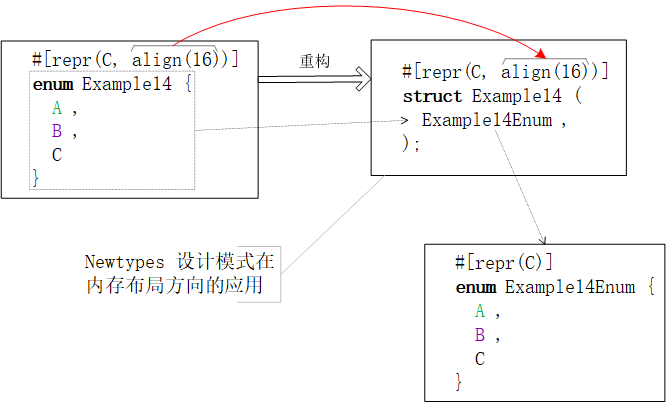
【Rust笔记】浅聊 Rust 程序内存布局
浅聊Rust程序内存布局 内存布局看似是底层和距离应用程序开发比较遥远的概念集合,但其对前端应用的功能实现颇具现实意义。从WASM业务模块至Nodejs N-API插件,无处不涉及到FFI跨语言互操作。甚至,做个文本数据的字符集转换也得FFI调用操作系统…...

玻璃生产过程中的窑内压力高精度恒定控制解决方案
摘要:在玻璃生产中对玻璃窑炉中窑压的要求极高,通常需要控制微正压4.7Pa(表压),偏差控制在0.3Pa,而窑炉压力还会受到众多因素的影响,所以实现高稳定性的熔窑压力控制具有很大难度,为…...

创意营销:初期推广的多种策略!
文章目录 🍊 预热🎉 制定预热计划和目标🎉 利用社交媒体传播🎉 创造独特的体验🎉 利用口碑营销🎉 定期发布更新信息🎉 案例说明 🍊 小范围推广🎉 明确目标用户群体&#…...
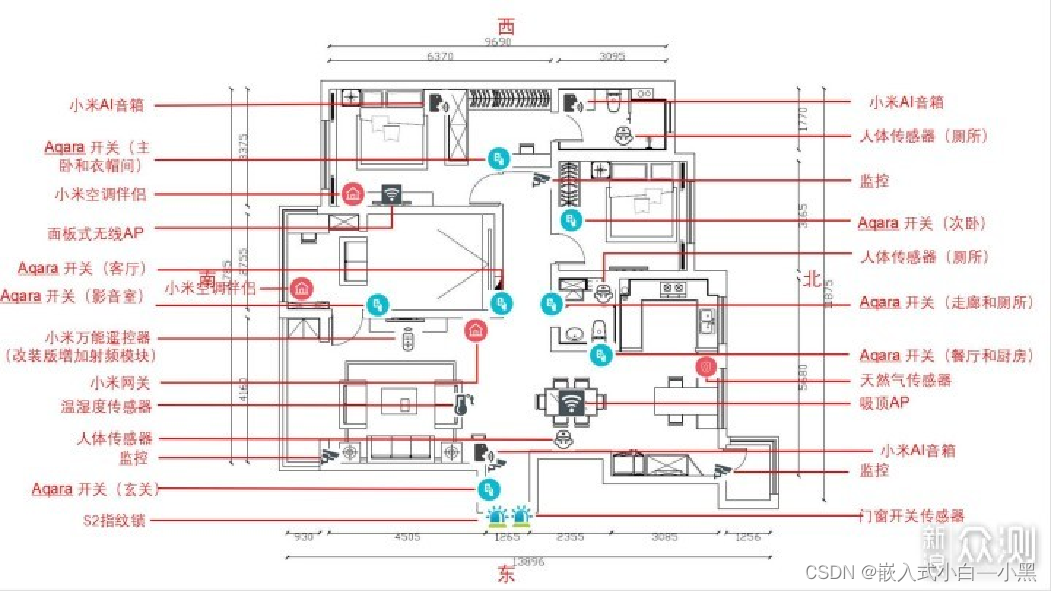
【小黑嵌入式系统第一课】嵌入式系统的概述(一)
文章目录 一、嵌入式系统基本概念计算机发展的三大阶段CPU——计算机的核心什么是嵌入式系统嵌入式系统的分类 二、嵌入式系统的特点三、嵌入式系统发展无操作系统阶段简单操作系统阶段实时操作系统阶段面向Internet阶段 四、嵌入式系统的应用工业控制 工业设备通信设备信息家电…...

RK平台使用MP4视频做开机动画以及卡顿问题
rk平台android11以后系统都可以使用MP4格式的视频做开机动画,系统源码里面默认使用的是ts格式的视频,其实使用mp4的视频也是可以的。具体修改如下: diff --git a/frameworks/base/cmds/bootanimation/BootAnimation.cpp b/frameworks/base/cmds/bootanimation/BootAnimat…...
通讯网关软件023——利用CommGate X2HTTP实现HTTP访问Modbus TCP
本文介绍利用CommGate X2HTTP实现HTTP访问Modbus TCP。CommGate X2HTTP是宁波科安网信开发的网关软件,软件可以登录到网信智汇(http://wangxinzhihui.com)下载。 【案例】如下图所示,SCADA系统上位机、PLC、设备具备Modbus RTU通讯接口,现在…...
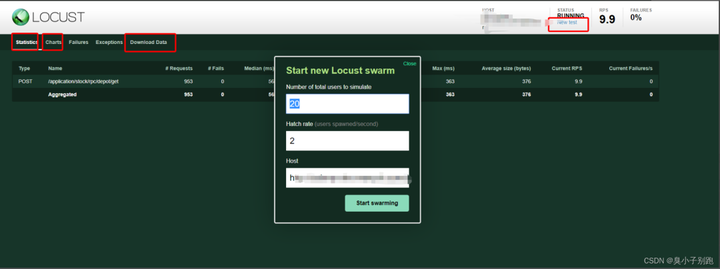
Python性能测试框架Locust实战教程!
01、认识Locust Locust是一个比较容易上手的分布式用户负载测试工具。它旨在对网站(或其他系统)进行负载测试,并确定系统可以处理多少个并发用户,Locust 在英文中是 蝗虫 的意思:作者的想法是在测试期间,放…...
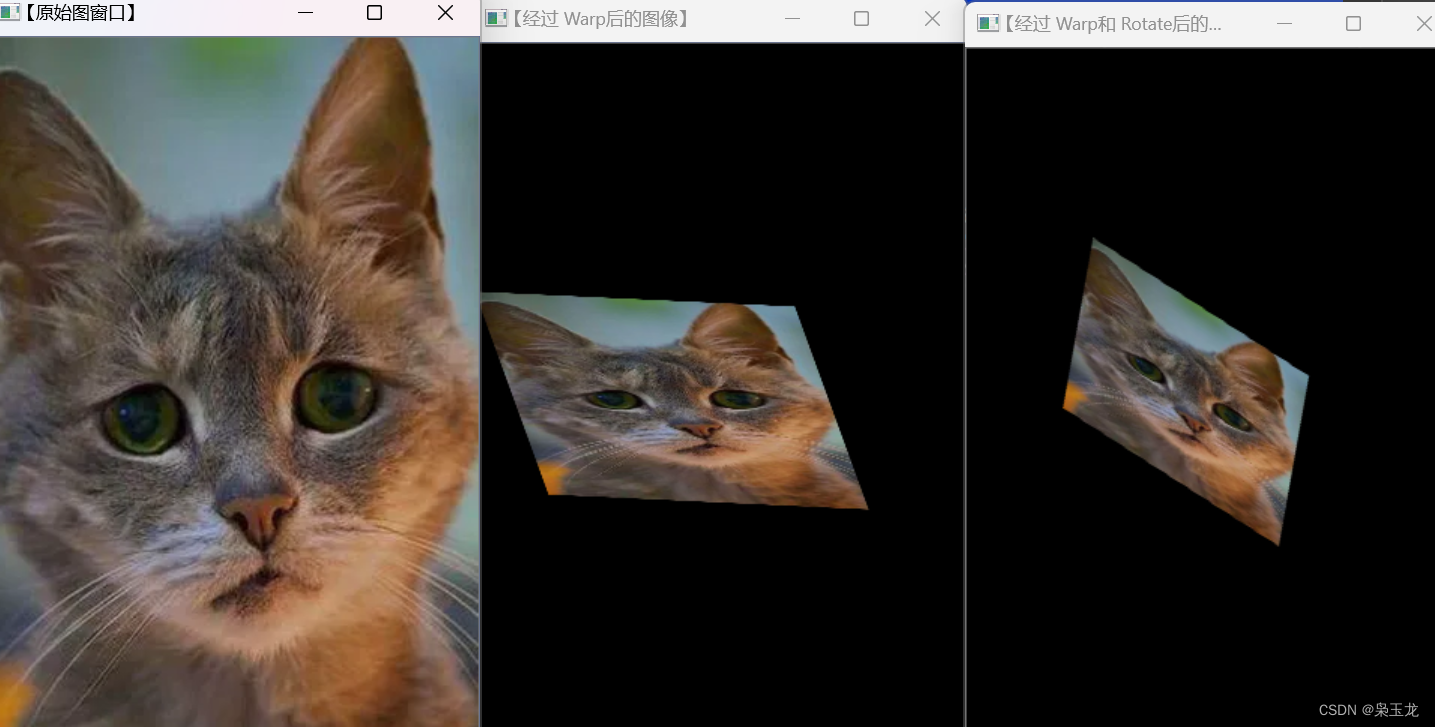
c++视觉处理---仿射变换和二维旋转变换矩阵的函数
仿射变换cv::warpAffine cv::warpAffine 是OpenCV中用于执行仿射变换的函数。仿射变换是一种线性变换,可用于执行平移、旋转、缩放和剪切等操作。下面是 cv::warpAffine 函数的基本用法: cv::warpAffine(src, dst, M, dsize, flags, borderMode, borde…...
)
uiautomator2遍历子元素.all()
当你获取了页面某个元素之后 elements d(’//*[clickable“true”]’).all() 返回的是一个list,其中是<uiautomator2.xpath.XMLElement>类型的变量。 可以通过以下方式获取它所有子类的信息。 for ele in elements:children ele.elem.getchildren()注意…...

【手写数据库toadb】SQL字符串如何被数据库认识? 词法语法分析基础原理,常用工具
词法语法分析 专栏内容: 手写数据库toadb 本专栏主要介绍如何从零开发,开发的步骤,以及开发过程中的涉及的原理,遇到的问题等,让大家能跟上并且可以一起开发,让每个需要的人成为参与者。 本专栏会定期更新,对应的代码也会定期更新,每个阶段的代码会打上tag,方便阶段…...

手把手教你基于windows系统使用GNVM进行node切换版本
GNVM是什么? GNVM 是一个简单的 Windows 下 Node.js 多版本管理器,类似的 nvm nvmw nodist 。 安装 进入官网,下载你所需要的包,直达链接 下载完成 放到我们的node环境包下,点击运行 请注意区分: 不存在 Node.js 环…...
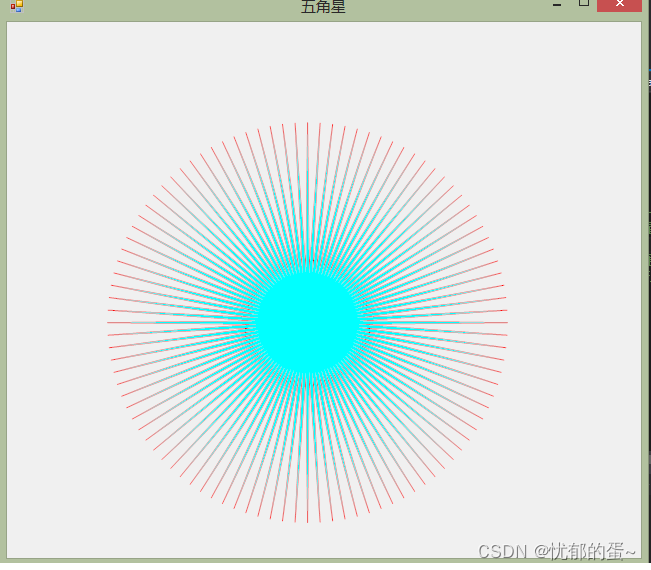
c#画五角星
c#画一个五角星,最重要的就是计算哪些坐标点出来,也是最难的一部分,这要涉及到一些数学方面的知识.对数学坐标知识不是很熟的人,如果想学画图,我建议多去看一下数学书,对我们写程序的人来说是没有什么坏处可言的. 想学习的朋友可以一起学习,我觉得分享学习是一种快乐,所以把自…...
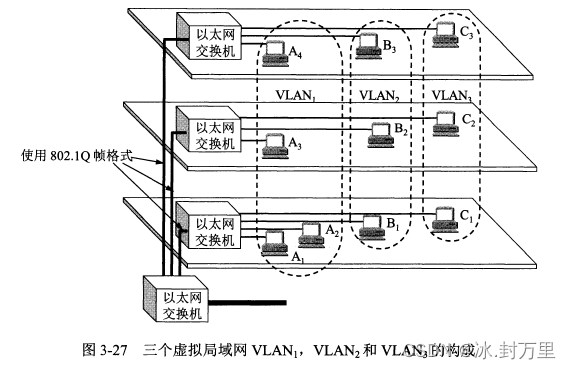
第三章 数据链路层 | 计算机网络(谢希仁 第八版)
文章目录 第三章 数据链路层3.1 使用点对点信道的数据链路层3.1.1 数据链路和帧3.1.2 三个基本问题 3.2 点对点协议PPP3.2.1 PPP协议的特点3.2.2 PPP协议的帧格式3.2.3 PPP协议的工作状态 3.3 使用广播信道的数据链路层3.3.1 局域网的数据链路层3.3.2 CSMA/CD协议3.3.3 使用集线…...

李沐机器学习环境配置相关
李沐机器学习环境配置相关 condapython环境安装指令安装miniconda安装cpu版本torch安装jupyter测试GPU是否可以使用 conda 退出 conda 环境 conda deactivate进入都d2l环境 conda activate d2l启动jupyter notebook: jupyter notebookpython 列出所有安装的包 pip lsit环…...
笔试选择题:文件描述符+ionde和动静态库)
零基础Linux_16(基础IO_文件)笔试选择题:文件描述符+ionde和动静态库
目录 一. 文件描述符等 1. Linux下两个进程可以同时打开同一个文件,这时如下描述错误的是: 2. 以下关于标准输入输出错误的描述正确的是 3. 以下描述正确的是 4. 以下描述正确的是 [多选] 5. 在bash中,在一条命令后加入”1>&2”…...

基于OpenCV的灰度图的图片相似度计算
from skimage.metrics import structural_similarity as ssim import matplotlib.pyplot as plt import cv2 def picture_recognization(imagname):# 读取两张图片image1 cv2.imread(D:/AutoTest/PythonProject/standard_img/ imagname)image2 cv2.imread(D:/AutoTest/Pytho…...
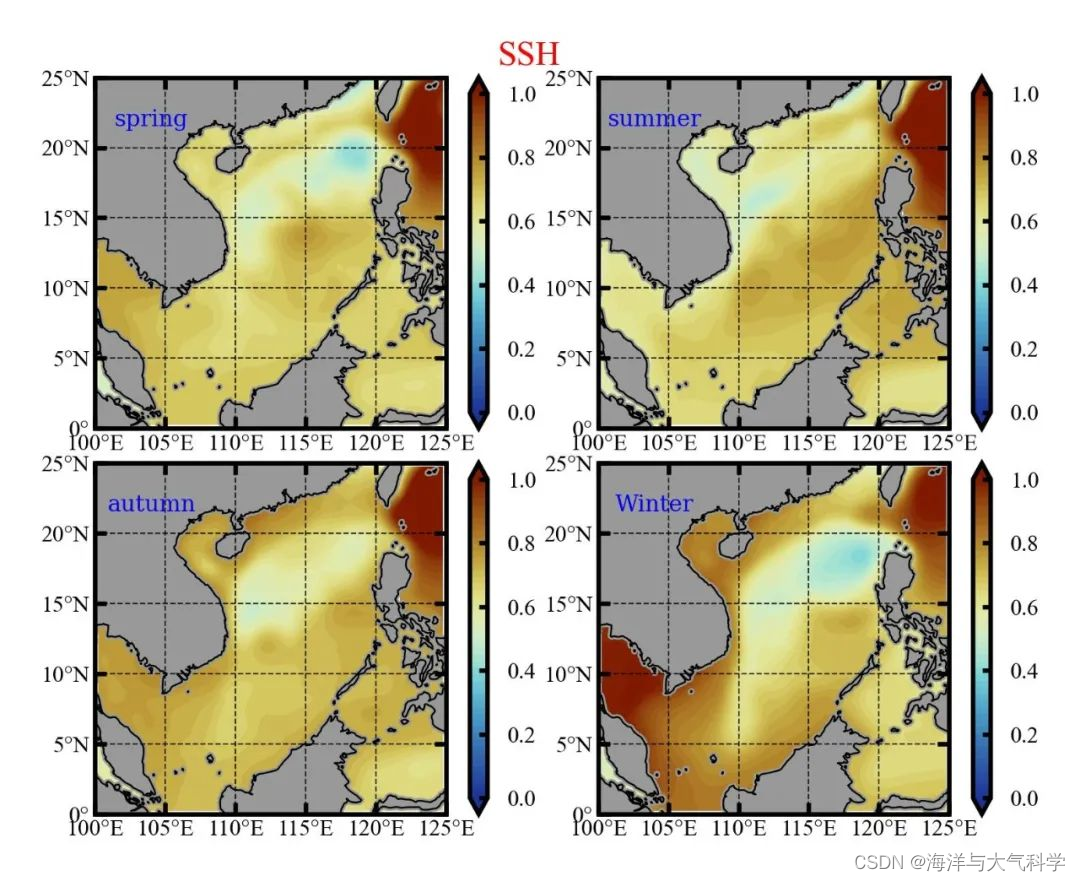
【python海洋专题二十】subplots_adjust布局调整
上期读取soda,并subplot 但是存在一些不完美,本期修饰 本期内容 subplots_adjust布局调整 1:未调整布局的 2:调整布局 往期推荐 【python海洋专题一】查看数据nc文件的属性并输出属性到txt文件 【python海洋专题二】读取水深…...
)
TensorFlow入门(二十四、初始化学习参数)
参数的初始化关系到网络能否训练出好的结果或者是以多快的速度收敛,对训练结果有着重要的影响。 初始化学习参数需要注意的规则 不可以将网络中的所有参数初始化为0,也不能全部初始化为同一个值。如果参数全部初始化为0或者是同一个值,会使得所有神经元的输出都是相同的,进而造…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
