如何进行大数运算和高精度计算?
大数运算和高精度计算是在计算机编程中常见的需求,尤其是当处理大整数、分数、复数、浮点数等需要更多位数的数据时。在C语言中,由于原生的数据类型有限,您需要使用自定义的数据结构和算法来执行大数运算和高精度计算。在本文中,我们将讨论大数运算的概念,以及如何在C语言中实现高精度计算。
大数运算的概念
大数运算是指对超出特定数据类型表示范围的数字进行数学运算。C语言中,整数类型(如int、long)的范围通常是有限的,因此无法处理非常大的整数或小数。在这种情况下,需要使用自定义的数据结构来表示和操作这些大数。
为什么需要大数运算?
大数运算在许多领域中都很有用,包括密码学、数论、科学计算、金融建模、数据分析等。以下是一些需要大数运算的情况:
-
密码学:许多加密算法,如RSA,涉及大质数的运算。这些质数通常非常大,需要大数运算。
-
科学计算:在科学研究中,可能需要处理非常大的数值数据,例如计算天文学、物理学或气象学中的数据。
-
金融建模:在金融领域,需要进行高精度的金融计算,如计算复利、估值、风险模型等。
-
统计分析:在统计学中,需要执行高精度的统计分析,如计算均值、方差、相关性等。
-
计算机代数系统:在计算机代数系统中,需要处理多项式、矩阵等数学对象,这可能包括大数。
如何表示大数?
大数通常表示为一个整数或浮点数的序列,其中每个数字位都有其位置和权重。例如,一个大整数可以表示为一个数字数组,其中每个元素代表一个位(如个位、十位、百位等)的值。对于小数,可以使用类似的方法,但每个元素表示小数点后的位置。
例如,大数 123456789012345678901234567890 可以表示为整数数组 [0, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0],其中数组的每个元素表示相应位置上的数字。
高精度计算的实现
高精度计算需要一种数据结构来存储大数,并定义用于执行算术运算(加法、减法、乘法、除法等)的函数。在C语言中,可以使用数组来表示大数,并实现运算函数来执行高精度计算。
以下是高精度计算的基本步骤:
-
表示大数:使用数组来存储大数,每个元素表示相应位置上的数字。通常,数组的每个元素可以存储0到9的整数。
-
实现运算:为大数实现基本的算术运算,如加法、减法、乘法和除法。这些运算需要逐位操作数组,并处理进位和借位。
-
处理特殊情况:在高精度计算中,需要考虑一些特殊情况,如负数处理、除法中的余数等。
-
优化:为了提高计算效率,可以采用一些优化技巧,如快速乘法算法、快速除法算法等。
下面,我们将演示如何实现高精度加法和乘法,以及处理负数的情况。
高精度加法
高精度加法的基本思想是从最低位(个位)开始逐位相加,并处理进位。以下是高精度加法的实现示例:
#include <stdio.h>// 假设每个数组元素可以存储0到9的整数
#define MAX_DIGITS 1000// 定义大数结构
typedef struct {int digits[MAX_DIGITS];int size;
} BigNum;// 初始化大数
void initBigNum(BigNum *num) {for (int i = 0; i < MAX_DIGITS; i++) {num->digits[i] = 0;}num->size = 0;
}// 执行高精度加法
void addBigNums(const BigNum *a, const BigNum *b, BigNum *result) {int carry = 0;for (int i = 0; i < MAX_DIGITS; i++) {int temp = a->digits[i] + b->digits[i] + carry;result->digits[i] = temp % 10;carry = temp / 10;}result->size = MAX_DIGITS;
}// 打印大数
void printBigNum(const BigNum *num) {int leadingZeros = 1;for (int i = MAX_DIGITS - 1; i >= 0; i--) {if (leadingZeros && num->digits[i] != 0) {leadingZeros = 0;}if (!leadingZeros) {printf("%d", num->digits[i]);}}if (leadingZeros) {printf("0");}printf("\n");
}int main() {BigNum num1, num2, result;initBigNum(&num1);initBigNum(&num2);initBigNum(&result);// 设置大
num2.digits[0] = 3;
num2.digits[1] = 4;
num2.size = 2;// 执行高精度加法
addBigNums(&num1, &num2, &result);// 打印结果
printf("Sum: ");
printBigNum(&result);return 0;
在上述示例中,我们首先定义了一个用于表示大数的结构`BigNum`。`initBigNum`函数用于初始化大数,`addBigNums`函数实现了高精度加法,`printBigNum`函数用于打印大数。在`main`函数中,我们初始化了两个大数`num1`和`num2`,并将它们的值设定为12和34。然后,我们调用`addBigNums`函数进行高精度加法,并将结果打印出来。在执行加法时,我们处理了进位的情况。### 高精度乘法高精度乘法的基本思想是模仿手工长除法的方法,逐位相乘并考虑进位。以下是高精度乘法的实现示例:```c
#include <stdio.h>// 假设每个数组元素可以存储0到9的整数
#define MAX_DIGITS 1000// 定义大数结构
typedef struct {int digits[MAX_DIGITS];int size;
} BigNum;// 初始化大数
void initBigNum(BigNum *num) {for (int i = 0; i < MAX_DIGITS; i++) {num->digits[i] = 0;}num->size = 0;
}// 执行高精度乘法
void multiplyBigNums(const BigNum *a, const BigNum *b, BigNum *result) {BigNum temp;initBigNum(&temp);for (int i = 0; i < a->size; i++) {int carry = 0;for (int j = 0; j < b->size; j++) {int product = a->digits[i] * b->digits[j] + temp.digits[i + j] + carry;temp.digits[i + j] = product % 10;carry = product / 10;}temp.digits[i + b->size] = carry;}*result = temp;
}// 打印大数
void printBigNum(const BigNum *num) {int leadingZeros = 1;for (int i = MAX_DIGITS - 1; i >= 0; i--) {if (leadingZeros && num->digits[i] != 0) {leadingZeros = 0;}if (!leadingZeros) {printf("%d", num->digits[i]);}}if (leadingZeros) {printf("0");}printf("\n");
}int main() {BigNum num1, num2, result;initBigNum(&num1);initBigNum(&num2);initBigNum(&result);// 设置大数的值num1.digits[0] = 1;num1.digits[1] = 2;num1.size = 2;num2.digits[0] = 3;num2.digits[1] = 4;num2.size = 2;// 执行高精度乘法multiplyBigNums(&num1, &num2, &result);// 打印结果printf("Product: ");printBigNum(&result);return 0;
}
在上述示例中,我们首先定义了一个用于表示大数的结构BigNum,并实现了初始化和打印大数的函数。然后,我们定义了一个multiplyBigNums函数,用于执行高精度乘法。
在main函数中,我们初始化了两个大数num1和num2,并将它们的值设定为12和34。然后,我们调用multiplyBigNums函数进行高精度乘法,并将结果打印出来。在执行乘法时,我们模仿手工长除法的方法,逐位相乘并处理进位。
处理负数的情况
处理负数的情况需要在大数运算中引入符号。通常,大数结构可以包含一个额外的成员来表示正负号。此外,需要相应地调整加法和乘法的算法来考虑符号。
例如,可以将BigNum结构扩展为以下形式:
typedef struct {int digits[MAX_DIGITS];int size;int isNegative; // 0表示正数,1表示负数
} BigNum;
然后,在进行大数运算时,需要在结果中记录符号,并根据需要执行相应的符号处理。
性能和优化
高精度计算通常需要大量的运算和内存,因此性能是一个重要的考虑因素。以下是一些性能和优化方面的注意事项:
-
位数限制:根据应用需求,可以限制大数的位数。不需要非常大的位数时,可以减小数组的大小,从而提高性能。
-
快速乘法和快速除法:使用快速乘法和快速除法算法可以减少操作次数,提高运算速度。
-
位操作:使用位运算(如移位操作)来加速高精度计算。
-
多线程:如果需要执行大量的高精度计算,可以考虑并行化计算以提高性能。
-
缓存:考虑缓存性能,尽量避免不必要的数据复制和内存访问。
-
数值表示:根据应用需求,可以选择不同的数值表示方式,如定点数、浮点数等。
-
**算法选择**:选择最适合特定问题的高精度计算算法。不同的问题可能需要不同的算法,如Karatsuba乘法、分治法等。
-
错误处理:在高精度计算中,需要考虑错误处理,包括溢出、除零等情况的处理。
-
内存管理:及时释放不再需要的内存,避免内存泄漏。
-
测试和调试:高精度计算的代码应该经过充分的测试和调试,以确保正确性和性能。
总之,高精度计算是一个复杂的领域,需要谨慎处理性能和优化问题。根据应用的具体需求,可以采取不同的优化策略来提高高精度计算的效率。
高精度计算的库和工具
为了简化高精度计算的实现,许多C语言库和工具已经提供了高精度计算的支持。以下是一些常用的高精度计算库和工具:
-
GNU Multiple Precision Arithmetic Library (GMP):GMP是一个广泛使用的开源库,提供了高精度整数和有理数的支持,可以用于执行加法、减法、乘法、除法等操作。
-
mpfr:MPFR是一个用于高精度浮点数运算的库,它提供了精确的浮点数计算和舍入控制。
-
Boost C++ Libraries:Boost库包含了
multiprecision模块,提供了高精度整数、有理数和浮点数的支持,可以在C++中使用。 -
Python:Python是一种高级编程语言,它内置了高精度整数和浮点数的支持。您可以使用Python来执行高精度计算,而不必担心底层实现。
-
SAGE:SAGE是一个数学计算工具,它提供了广泛的高精度计算功能,包括代数、数论、代数几何等领域的计算。
这些库和工具提供了高效且经过充分测试的高精度计算功能,可以极大地简化开发高精度计算应用程序的过程。您可以选择适合您需求的工具或库,以减少自己实现高精度计算的工作量。
总结
在C语言中,实现大数运算和高精度计算需要自定义数据结构和算法。您可以使用数组来表示大数,并实现加法、减法、乘法、除法等运算函数。同时,需要考虑性能和优化,以提高计算效率。如果您不希望自己实现高精度计算,可以考虑使用现有的高精度计算库和工具,它们提供了方便的接口和高性能的实现,以满足各种应用需求。高精度计算是一个广泛应用于数学、科学、工程和计算机科学等领域的重要概念,对于处理大数、高精度浮点数等数据具有重要价值。
相关文章:

如何进行大数运算和高精度计算?
大数运算和高精度计算是在计算机编程中常见的需求,尤其是当处理大整数、分数、复数、浮点数等需要更多位数的数据时。在C语言中,由于原生的数据类型有限,您需要使用自定义的数据结构和算法来执行大数运算和高精度计算。在本文中,我…...

身份证读卡器跟OCR有何区别?哪个好?
二代身份证读卡器(以下简称读卡器)和OCR(光学字符识别)是两种常见的身份证信息获取技术,它们在原理、功能和应用方面存在一些区别。下面将详细介绍二者的区别并探讨哪个更好。 1. 原理: - 读卡器ÿ…...
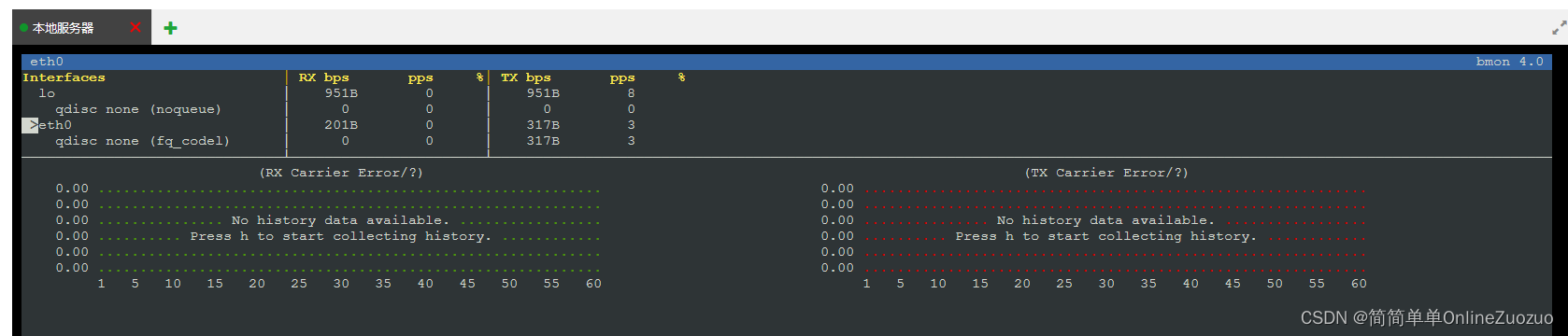
华为云云耀云服务器L实例评测 | 实例评测使用之硬件参数评测:华为云云耀云服务器下的 Linux 网络监控神器 bmon
华为云云耀云服务器L实例评测 | 实例评测使用之硬件参数评测:华为云云耀云服务器下的 Linux 网络监控神器 bmon 介绍华为云云耀云服务器 华为云云耀云服务器 (目前已经全新升级为 华为云云耀云服务器L实例) 华为云云耀云服务器是什…...

C++ 设计模式 —— 组合模式
C 设计模式 —— 组合模式 0. 引用连接 本文主要的思路和代码,来自于对以下连接的学习和实现: 组合模式 1. 引言 1.1 什么是组合模式? 组合模式的定义组合模式的作用 组合模式是一种行为型设计模式,它将对象组合成树形结构以…...
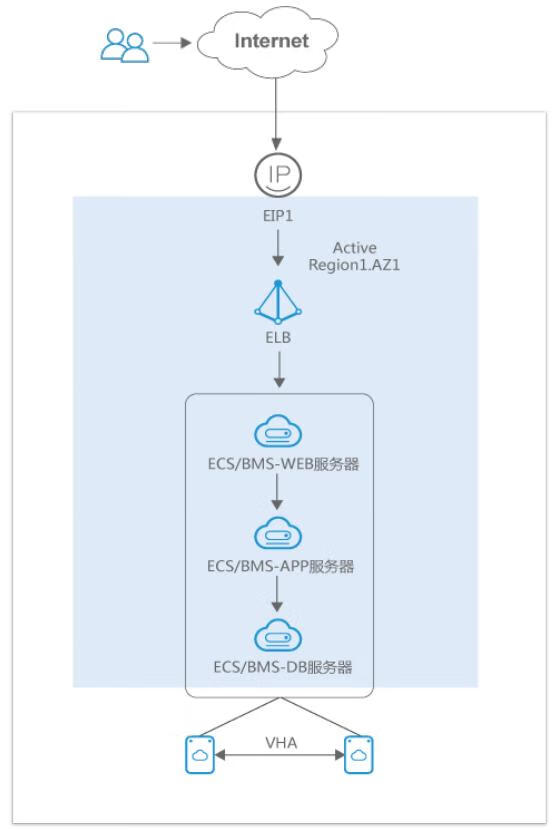
华为云Stack的学习(九)
十、华为云Stack灾备服务介绍 1.云硬盘备份VBS 云硬盘备份服务(VBS,Volume Backup Service)可为云硬盘(EVS,Elastic Volume Service)创建备份,利用备份数据恢复云硬盘,最大限度保障…...

Flink中jobmanager、taskmanager、slot、task、subtask、Parallelism的概念
场景 一个工厂有三个车间每个车间两条生产线 生产流程如下 原料->加工->过滤->分类->美化->包装->下线 JobManager:工厂 在上述场景中,工厂就是jobManager,负责协调、调度和监控整个生产过程 TaskManager:车间…...
OpenHarmony docker环境搭建
OpenHarmony docker环境搭建 要求一台安装ubuntu的虚拟机,vscode软件 安装docker 在 Ubuntu 上安装 Docker 非常直接。我们将会启用 Docker 软件源,导入 GPG key,并且安装软件包。 首先,更新软件包索引,并且安装必要的依赖软件…...
)
【计算机网络】网络编程接口 Socket API 解读(11)
Socket 是网络协议栈暴露给编程人员的 API,相比复杂的计算机网络协议,API 对关键操作和配置数据进行了抽象,简化了程序编程。 本文讲述的 socket 内容源自 Linux man。本文主要对各 API 进行详细介绍,从而更好的理解 socket 编程。…...
Qt工具开发,该不该跳槽?
Qt工具开发,该不该跳槽? 就这样吧,我怕你跳不动。 嵌入式UI,目前趋势是向着LVGL发展。QT已经在淘汰期了。很多项目还在用,但技术上已经落后。QT短期内不会全面淘汰,但退位让贤的大趋势已经很清楚了。 最近很多小伙伴…...
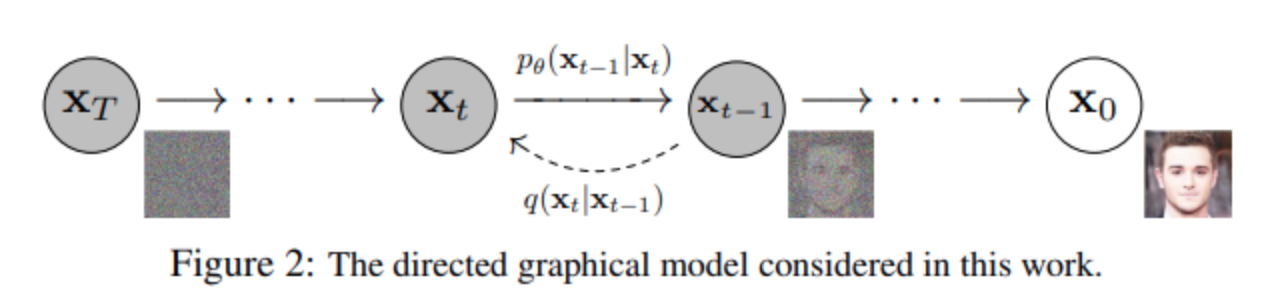
【深度学习】DDPM,Diffusion,概率扩散去噪生成模型,原理解读
看过来看过去,唯有此up主,非常牛: Video Explaination(Chinese) 1. DDPM Introduction q q q - 一个固定(或预定义)的正向扩散过程,逐渐向图像添加高斯噪声,直到最终得到纯噪声。 p θ p_θ p…...

HT8699:内置 BOOST 升Y双声道音频功率放大器
HT8699是一款内置BOOST升Y模块的立体声音频功率放大器。HT8699具有AB类和D类切换功能,在受到D类功放EMI干扰困扰时,可切换至AB类音频功放模式。 在D类模式下,内置的BOOST升Y模块可通过外置电阻调节升Y值,即使是锂电池供电…...

利达卓越:关注环保事业,持续赋能科技
随着全球环境问题的日益突出,绿色金融作为一种新兴的金融模式逐渐受到各国的重视。绿色金融是指在金融活动中,通过资金、信贷和风险管理等手段,支持环境友好和可持续发展的项目和产业。绿色金融的出现是为了应对气候变化、资源短缺、污染问题等现实挑战,促进经济的绿色转型和可…...

Spring MVC中通过配置文件配置定时任务
Spring MVC中配置定时任务(配置文件方式) 1.步骤 1.步骤 1-1 在springmvc.xml(配置文件)的beans中添加 xmlns:task"http://www.springframework.org/schema/task" http://www.springframework.org/schema/task http…...

AI项目十六:YOLOP 训练+测试+模型评估
若该文为原创文章,转载请注明原文出处。 通过正点原子的ATK-3568了解到了YOLOP,这里记录下训练及测试及在onnxruntime部署的过程。 步骤:训练->测试->转成onnx->onnxruntime部署测试 一、前言 YOLOP是华中科技大学研究团队在2021年…...
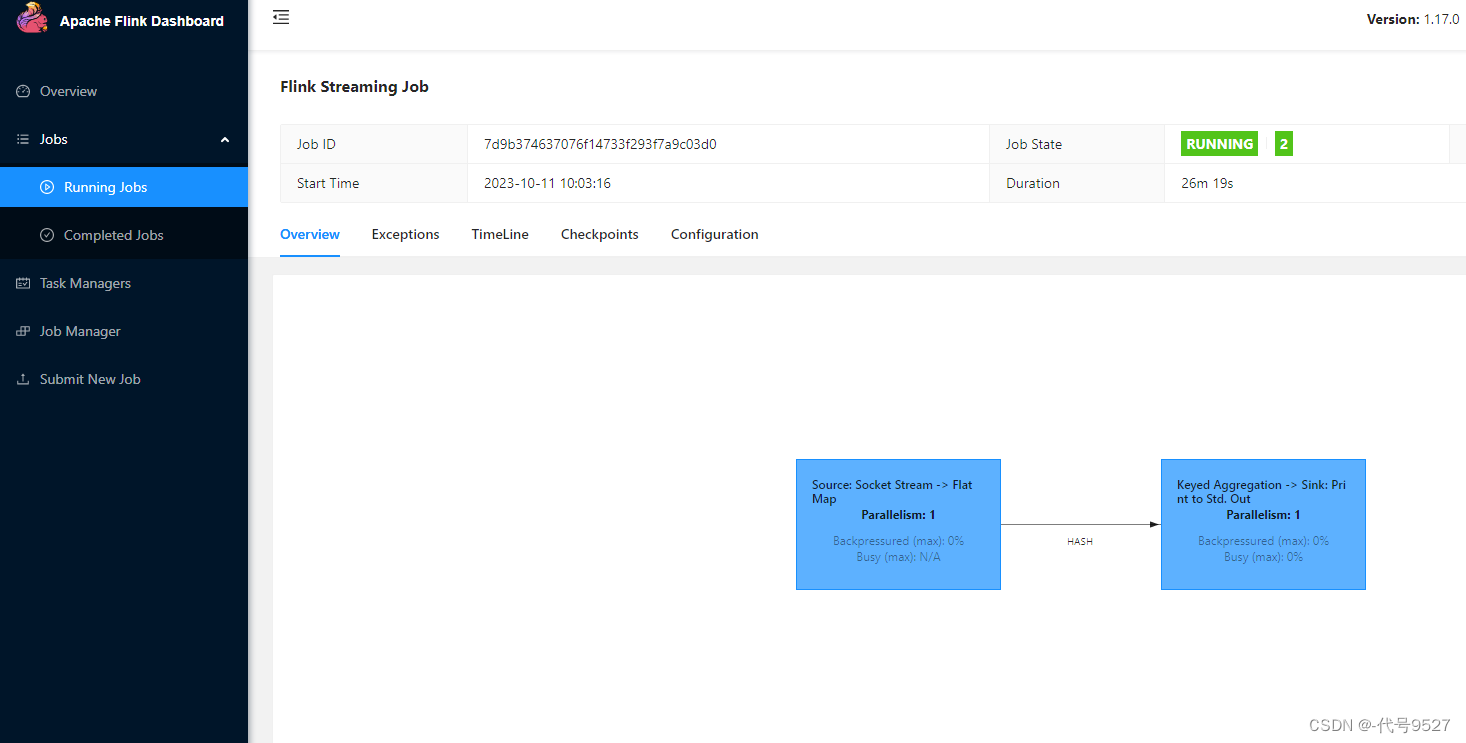
Flink报错could not be loaded due to a linkage failure
文章目录 1、报错2、原因3、解决 1、报错 在Flink上提交作业,点Submit没反应,F12看到接口报错信息为: 大概意思是,由于链接失败,无法加载程序的入口点类xx。没啥鸟用的信息,去日志目录继续分析:…...
网络工程师--网络安全与应用案例分析
前言 需要网络安全学习资料的点击链接:【282G】网络安全&黑客技术零基础到进阶全套学习大礼包,免费分享! 案例一: 某单位现有网络拓扑结构如下图所示,实现用户上网功能,该网络使用的网络交换机均为三…...

了解油封对汽车安全的影响?
油封也称为轴封或径向轴封,是车辆发动机、变速箱和其他各种机械系统中的重要部件。它们的主要功能是阻止重要发动机部件的液体(例如油或冷却剂)泄漏,同时防止污染物进入。这些看似简单的任务,但对汽车的安全性和可靠性有着深远的影响。 油封…...

创邻科技Galaxybase—激活数据要素的核心引擎
10月11日下午,创邻科技创始人张晨博士受杭州电子科技大学邀请,前往杭电校园开展交流分享。交流会中,张晨博士为现场的师生带来一场题为《图数据库——激活数据要素的新基建》的精彩分享,探讨数字经济时代底层技术的创新价值与图技…...
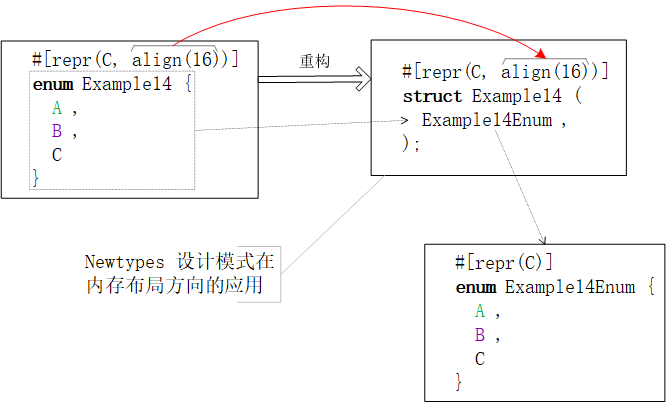
【Rust笔记】浅聊 Rust 程序内存布局
浅聊Rust程序内存布局 内存布局看似是底层和距离应用程序开发比较遥远的概念集合,但其对前端应用的功能实现颇具现实意义。从WASM业务模块至Nodejs N-API插件,无处不涉及到FFI跨语言互操作。甚至,做个文本数据的字符集转换也得FFI调用操作系统…...

玻璃生产过程中的窑内压力高精度恒定控制解决方案
摘要:在玻璃生产中对玻璃窑炉中窑压的要求极高,通常需要控制微正压4.7Pa(表压),偏差控制在0.3Pa,而窑炉压力还会受到众多因素的影响,所以实现高稳定性的熔窑压力控制具有很大难度,为…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
