【数据结构】二叉树--链式结构的实现 (遍历)
目录
一 二叉树的遍历
1 构建一个二叉树
2 前序遍历
3 中序遍历
4 后续遍历
5 层序
6 二叉树销毁
二 应用(递归思想)
1 二叉树节点个数
2 叶子节点个数
3 第K层的节点个数
4 二叉树查找值为x的节点
5 判断是否是二叉树
一 二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉 树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历 是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础
二叉树是: 1. 空树 2. 非空:根节点,根节点的左子树、根节点的右子树组成的。
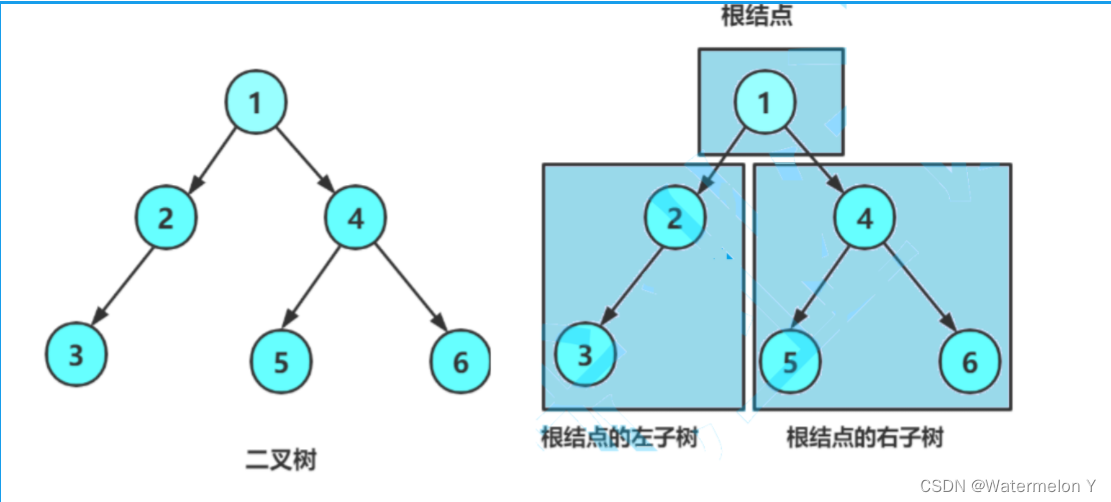
前序、中序以及后序遍历:
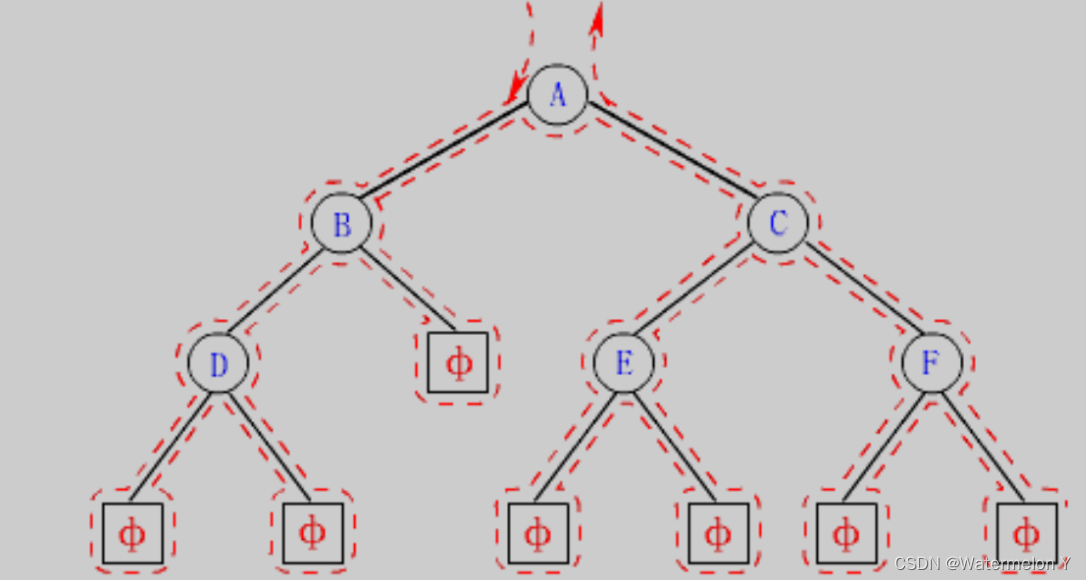
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为 根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
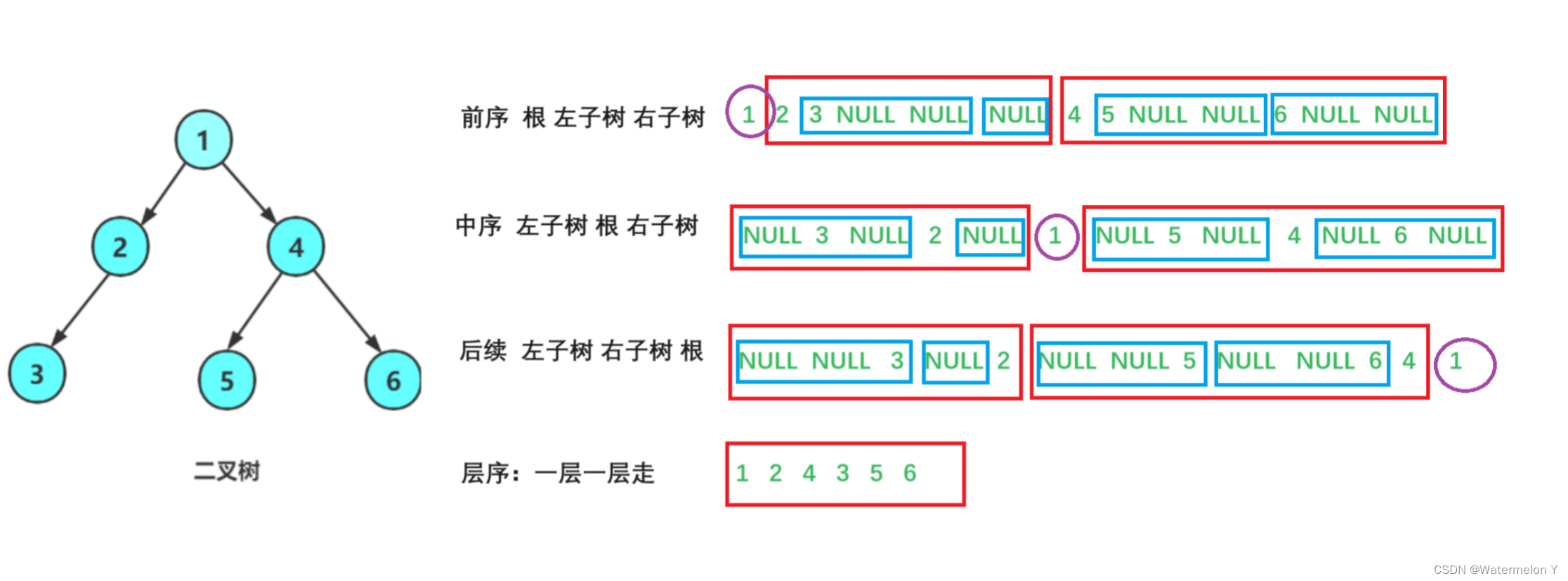
代码实现:
1 构建一个二叉树
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;int val;
}BTNode;BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");exit(-1);}node->left = NULL;node->right = NULL;node->val = x;return node;
}int main()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;PrevOrder(node1);printf("\n");InOrder(node1);printf("\n");PostOrder(node1);printf("\n");return 0;
}2 前序遍历
//前序遍历
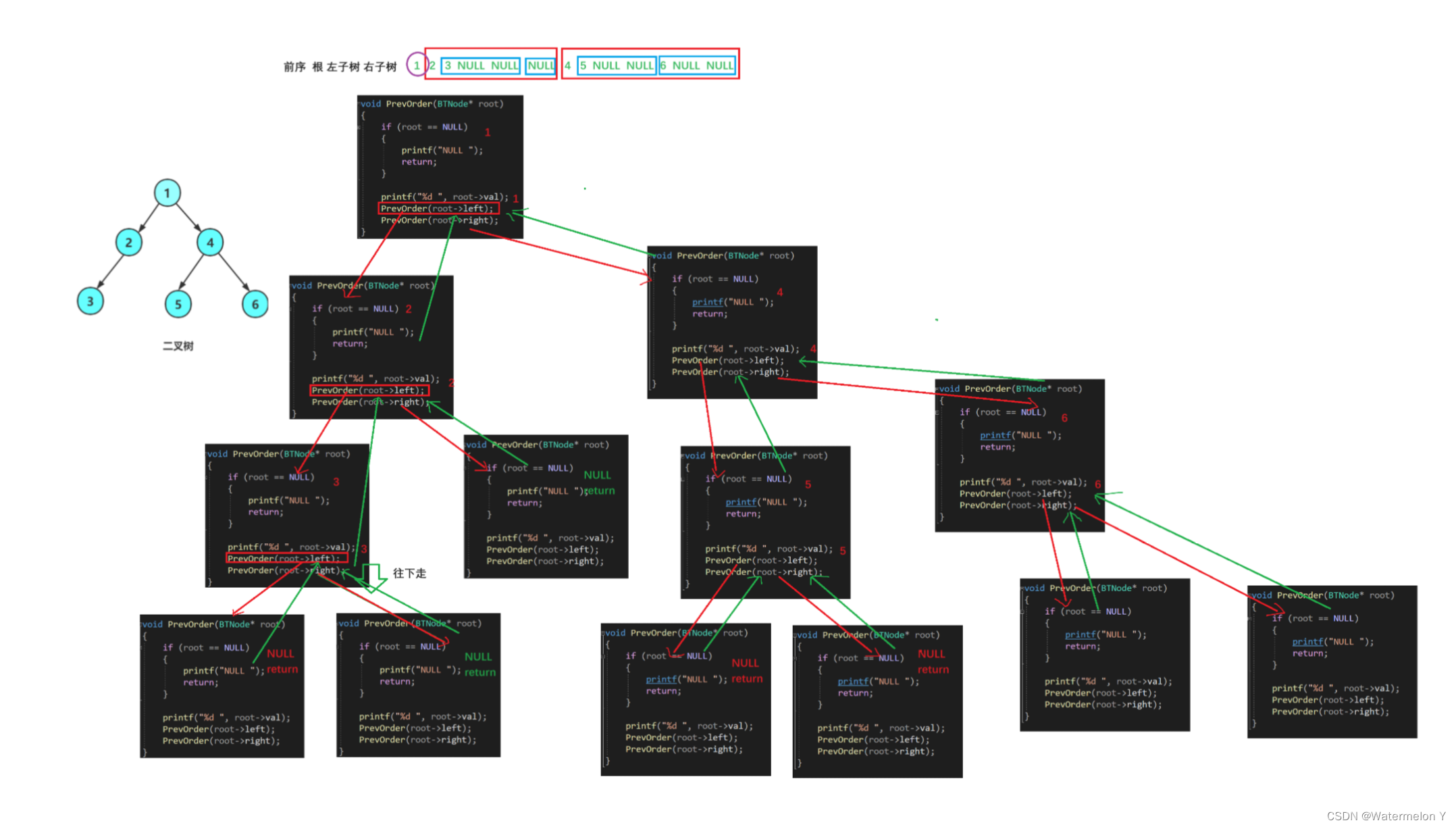
void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->val);PrevOrder(root->left);PrevOrder(root->right);
}

3 中序遍历
//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}
4 后续遍历
//后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}
5 层序

void QueueInit(Que* pq)
{assert(pq);pq->head = pq->tail = NULL;pq->size = 0;
}void QueuePush(Que* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->next = NULL;newnode->val = x;if (pq->tail == NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++;}bool QueueEmpty(Que* pq)
{assert(pq);return pq->head == NULL;
}void QueuePop(Que* pq)
{assert(pq);assert(!QueueEmpty(pq));if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* next = pq->head->next;free(pq->head);pq->head = next;}pq->size--;
}QDataType QueueFront(Que* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->val;
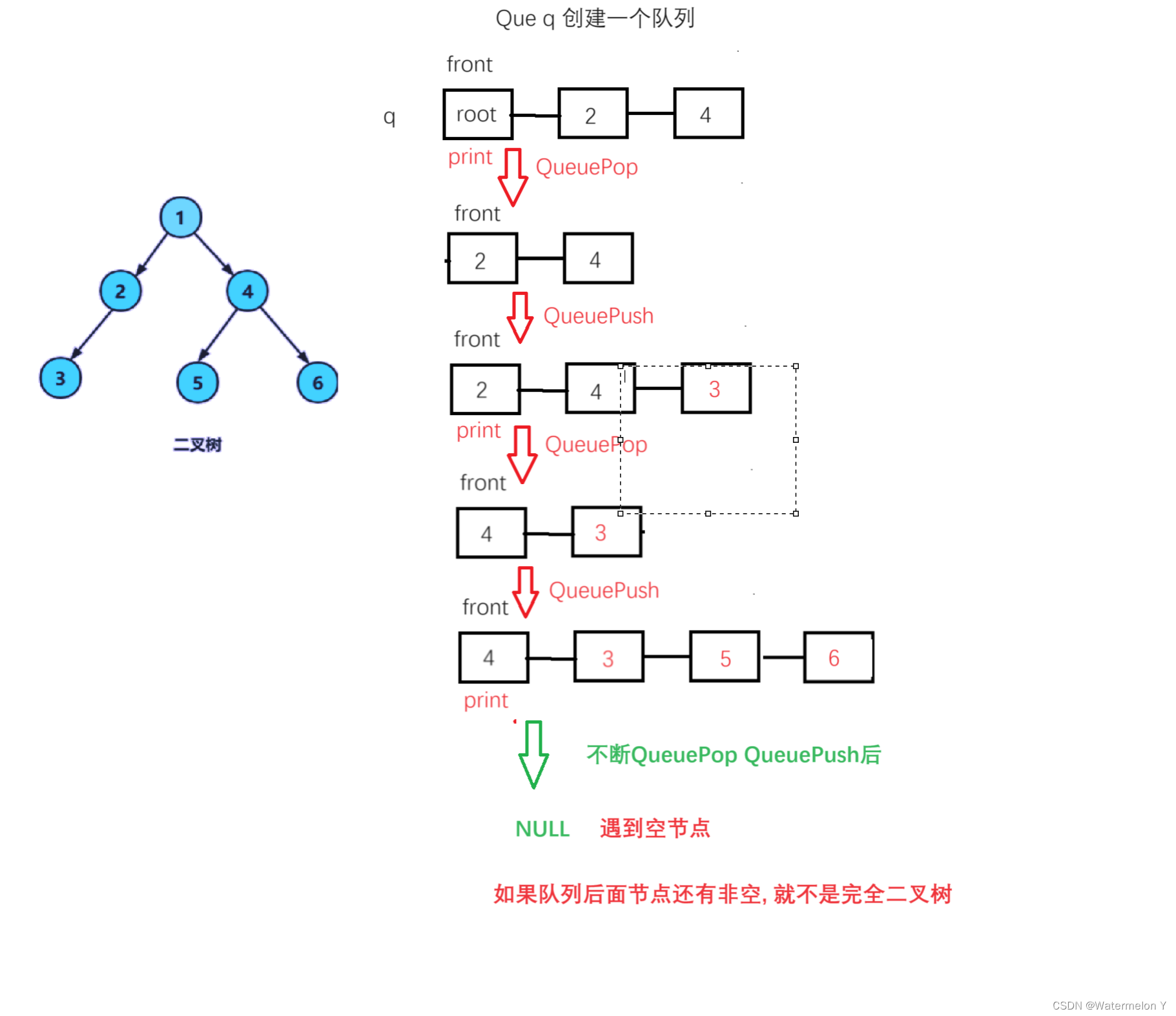
}void LevelOrder(BTNode* root)
{Que q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);printf("%d ", front->val);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}QueuePop(&q);}
}

6 二叉树销毁
//二叉树的销毁
void TreeDestroy(BTNode* root)
{if (root == NULL){return;}TreeDestroy(root->left);TreeDestroy(root->right);free(root);}二 应用(递归思想)
1 二叉树节点个数
int size = 0;
int TreeSize(BTNode* root)
{if (root == NULL){return 0;}else{size++;}TreeSize(root->left);TreeSize(root->right);return size;}我们还可以改进
int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
2 叶子节点个数
int TreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}3 第K层的节点个数
int TreeKLevel(BTNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}return TreeKLevel(root->left, k-1) + TreeKLevel(root->right, k-1);
}

4 二叉树查找值为x的节点
BTNode* TreeFind(BTNode* root, int x)
{if (root == NULL){return NULL;}if (root->val == x){return root;}BTNode* ret = NULL;//从左树找 找到了就返回 不找右树了ret = TreeFind(root->left, x);if (ret){return ret;}//左树没找到 就开始找右树ret = TreeFind(root->right, x);if (ret){return ret;}}5 判断是否是二叉树
void QueueInit(Que* pq)
{assert(pq);pq->head = pq->tail = NULL;pq->size = 0;
}void QueueDestroy(Que* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->head = pq->tail = NULL;pq->size = 0;
}void QueuePush(Que* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->next = NULL;newnode->val = x;if (pq->tail == NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++;}bool QueueEmpty(Que* pq)
{assert(pq);return pq->head == NULL;
}void QueuePop(Que* pq)
{assert(pq);assert(!QueueEmpty(pq));if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* next = pq->head->next;free(pq->head);pq->head = next;}pq->size--;
}QDataType QueueFront(Que* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->val;
}int TreeComplete(BTNode* root)
{Que q;QueInit(&q);if (root != NULL){QueuePush(&q, root);}//找空节点while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);if (front == NULL){break;}QueuePush(&q, front->left);QueuePush(&q, front->right);QueuePop(&q);}//已经找到空节点while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}
二叉树的链式结构的本质思想是递归, 对于递归不了解的小伙伴可以看看我之前的博客, 也可以自己尝试画一下递归展开图,下一节讲OJ题目.实战才最有效!继续加油!
相关文章:

【数据结构】二叉树--链式结构的实现 (遍历)
目录 一 二叉树的遍历 1 构建一个二叉树 2 前序遍历 3 中序遍历 4 后续遍历 5 层序 6 二叉树销毁 二 应用(递归思想) 1 二叉树节点个数 2 叶子节点个数 3 第K层的节点个数 4 二叉树查找值为x的节点 5 判断是否是二叉树 一 二叉树的遍历 学习二叉树结构࿰…...

reids基础数据结构
文章目录 一.整体1.RedisDb2.对象头 二.string三.list1.ziplist2.quicklist 四.hash五.set六.zset1.查找2.插入3.删除4.更新5.元素排名 一.整体 1.RedisDb redis内部的所有键值对是两个hash结构,维护了键值对和过期时间 dict *dictdict *expire 2.对象头 int t…...

gitlab 维护
一 环境信息 二 日常维护 2.1 gitlab mirror 2.1.1 常见方法 社区版本gitab mirror 只能push,默认限制了局域网内mirror 需要修改admin/setting/network(网络)/outbound(出站请求) 勾选允许局域网即可。 2.1.2 疑难问题 内网有三个gitlab A: GITLAB 12 B\C GI…...
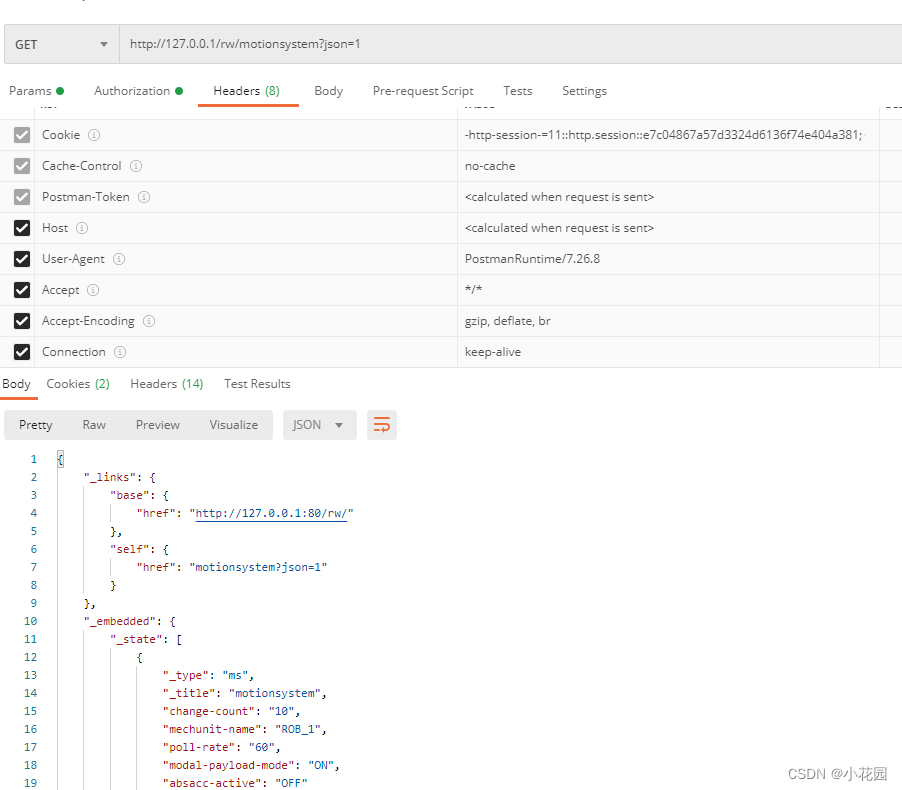
ABB机器人RWS连接方法
目录 方法一:curl 方法二:网页地址 方法三:Postman 与ABB机器人通讯,较新机器人,可以使用Robot Web Services,直接方便地使用网页进行查看当前数据,但是网页需要用户名密码验证,测…...

Spring Boot的循环依赖问题
目录 1.循环依赖的概念 2.解决循环依赖的方法 1.构造器方法注入: 2.Lazy注解 3.DependsOn注解 1.循环依赖的概念 两个或多个bean之间互相依赖,形成循环,此时,Spring容器无法确定先实例化哪个bean,导致循环依赖的…...

postgresql|数据库|恢复备份的时候报错:pg_restore: implied data-only restore的处理方案
一, 前情回顾 某次在使用pg_dump命令逻辑备份出来的备份文件对指定的几个表恢复的时候,报错pg_restore: implied data-only restore 当然,遇到问题首先就是百度了,但好像没有什么明确的解决方案,具体的报错命令和…...
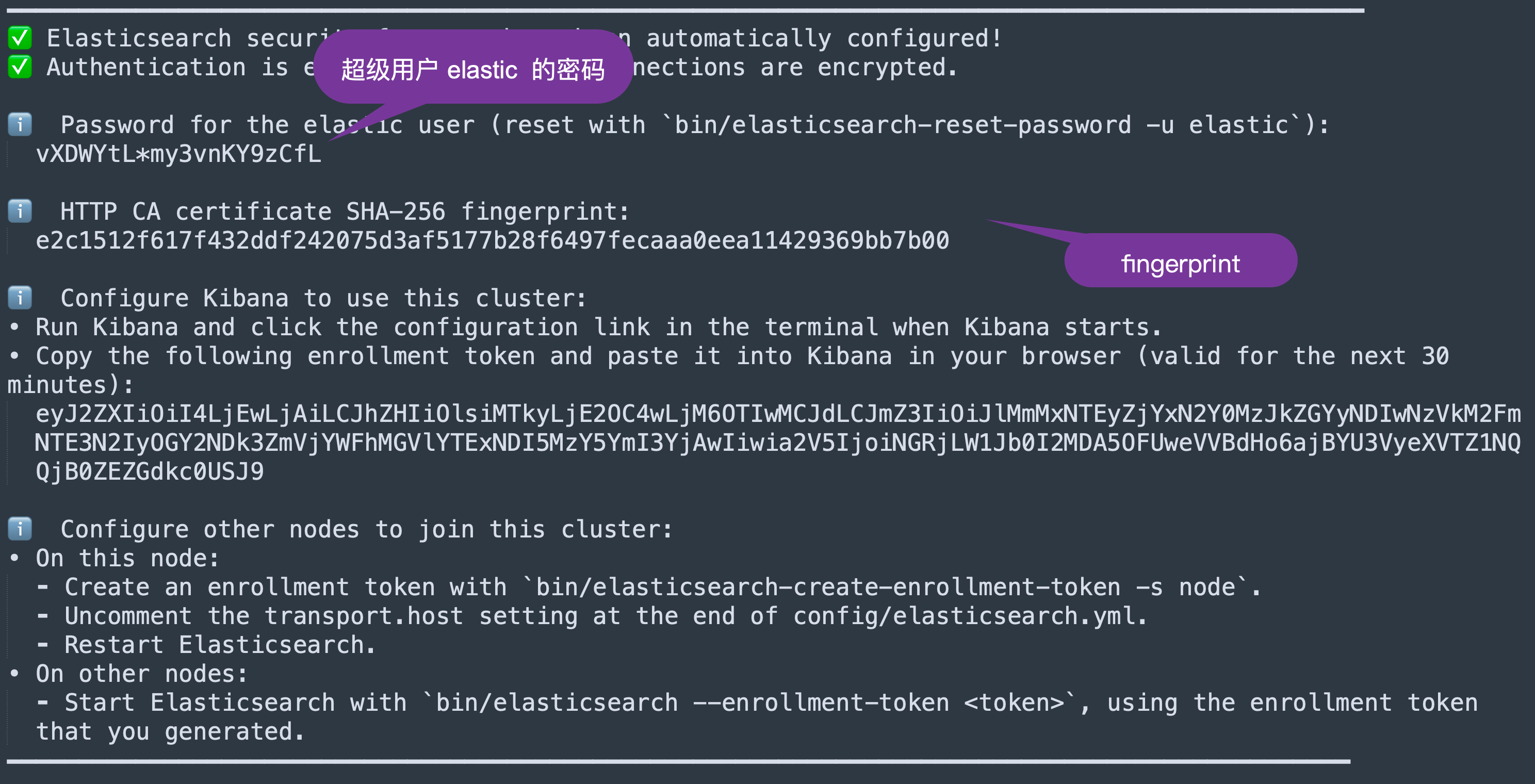
Elasticsearch:使用 Langchain 和 OpenAI 进行问答
这款交互式 jupyter notebook 使用 Langchain 将虚构的工作场所文档拆分为段落 (chunks),并使用 OpenAI 将这些段落转换为嵌入并将其存储到 Elasticsearch 中。然后,当我们提出问题时,我们从向量存储中检索相关段落,并使用 langch…...

安全巡检管理系统—隐患排查治理
安全管理越来越重要,每个生产企业都需要一个安全隐患排查治理小程序!利用凡尔码平台搭建安全巡检管理系统主要有以下四个功能 1、制定巡检计划:安全巡检管理系统可以帮助用户制定巡检计划,用户可以根据需要创建不同的计划…...
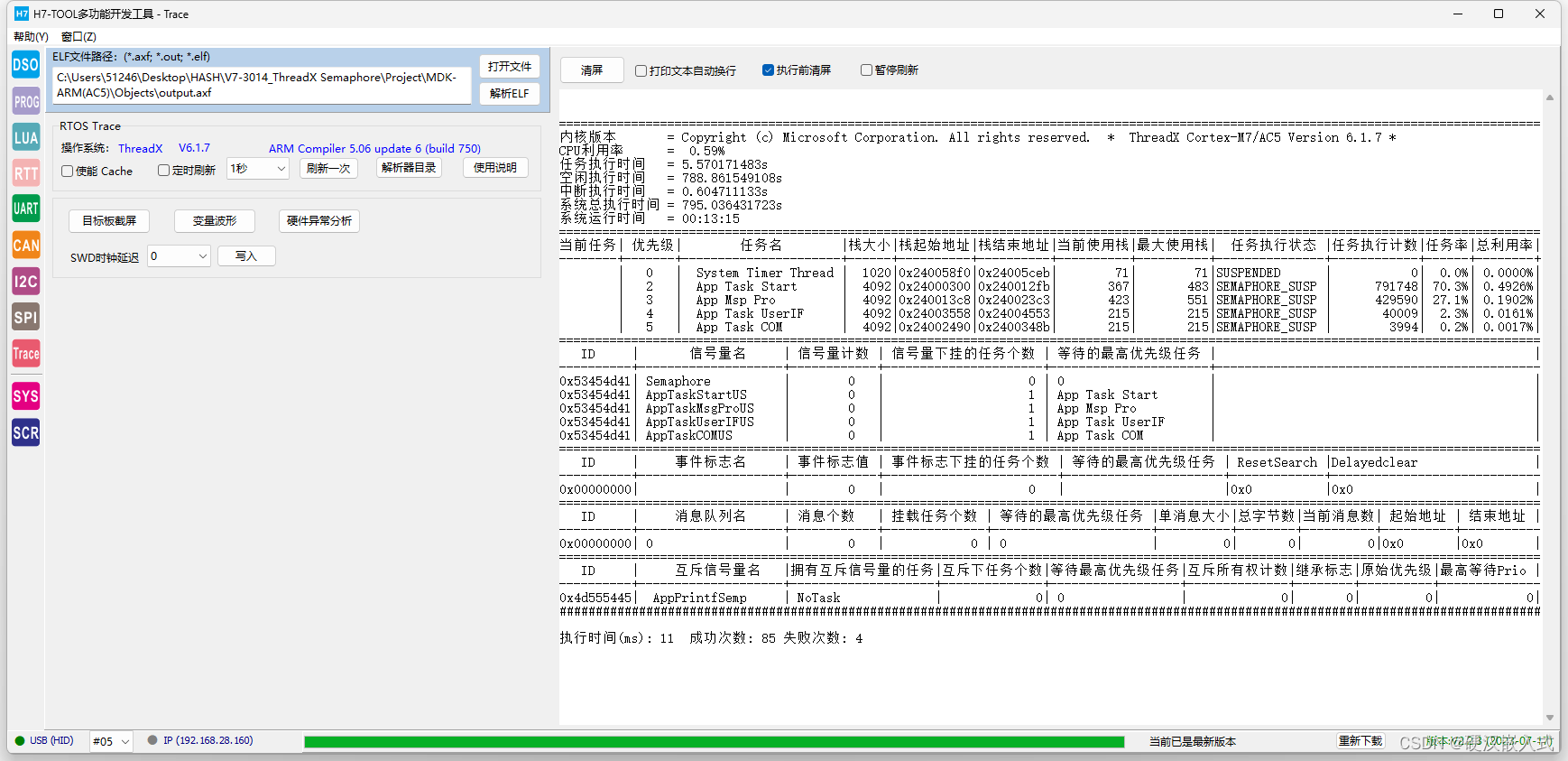
第9期ThreadX视频教程:自制个微秒分辨率任务调度实现方案(2023-10-11)
视频教程汇总帖:【学以致用,授人以渔】2023视频教程汇总,DSP第12期,ThreadX第9期,BSP驱动第26期,USB实战第5期,GUI实战第3期(2023-10-11) - STM32F429 - 硬汉嵌入式论坛 …...

C++ 11 lamdba表达式详解
C lamdba 表达式 Lambda表达式是C11引入的一个新特性,它允许我们在需要函数对象的地方,使用一种更加简洁的方式定义匿名函数。Lambda表达式通常用于STL中的算法、回调函数、事件处理程序等场合。 Lambda表达式的基本语法为: Copy Code[captu…...

Linux运行环境搭建系列-Zookeeper安装
Zookeeper安装 ## 下载Zookeeper:https://zookeeper.apache.org/releases.html https://dlcdn.apache.org/zookeeper/zookeeper-3.8.3/apache-zookeeper-3.8.3-bin.tar.gz ## 解压 tar -zxvf apache-zookeeper-3.8.3-bin.tar.gz ## 删除原文件,重命名 r…...

vscode利用lauch.json和docker中的delve调试本地crdb
---- vscode利用delve调试crdb 创建了一个delve容器用于debug crdbdelve: Delve是一个用于Go编程语言的调试器。它提供了一组命令和功能,可以帮助开发人员在调试过程中检查变量、设置断点、单步执行代码等操作。Delve可以与Go程序一起使用,…...

【java|golang】多字段排序以及排序规则
奖励最顶尖的 K 名学生 给你两个字符串数组 positive_feedback 和 negative_feedback ,分别包含表示正面的和负面的词汇。不会 有单词同时是正面的和负面的。 一开始,每位学生分数为 0 。每个正面的单词会给学生的分数 加 3 分,每个负面的词…...
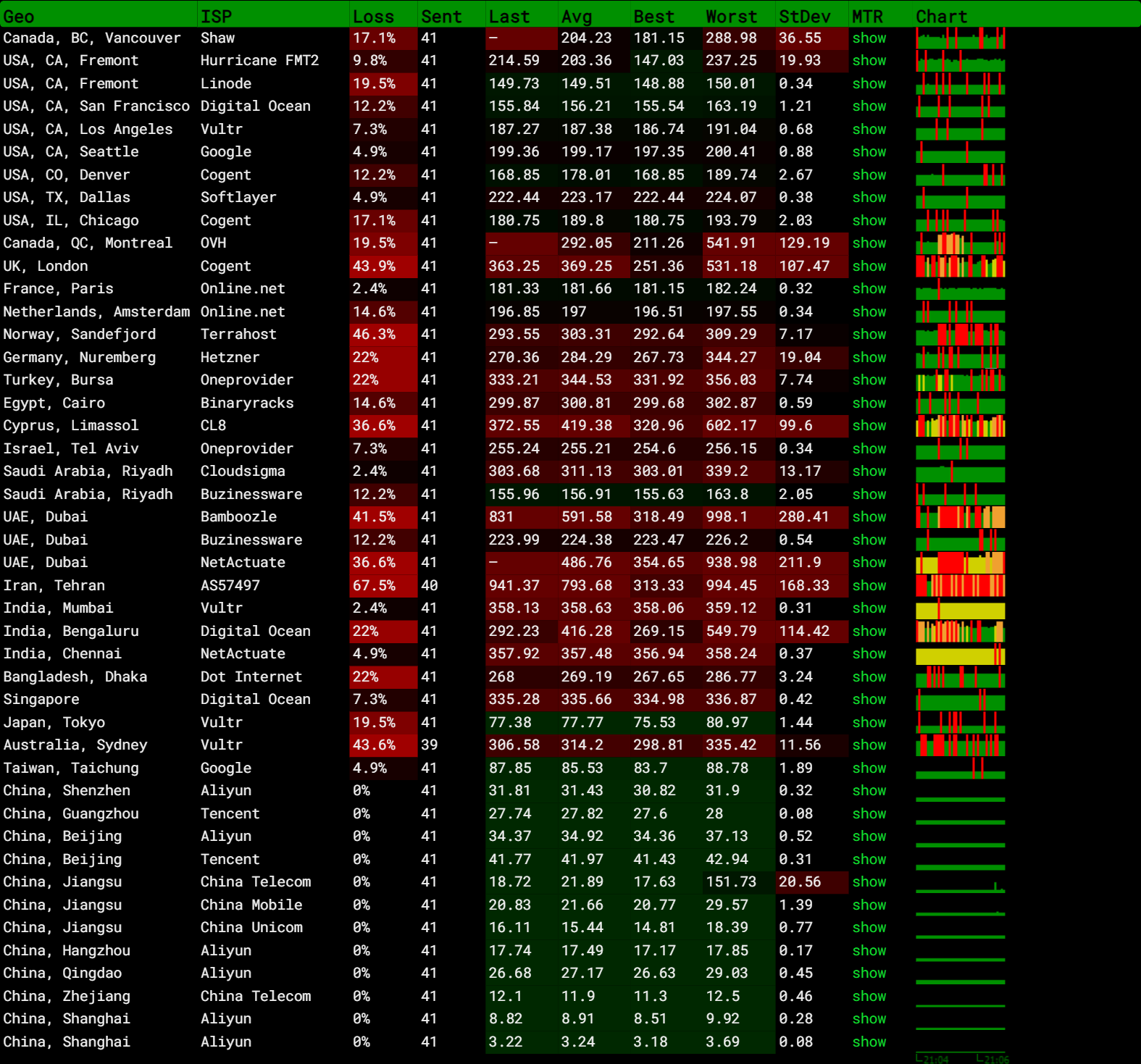
腾讯云 轻量云 上海 VPS 测评
description: 发布于 2023-07-05腾讯云 轻量云 上海 VPS 测评 腾讯云国内机非常稳定,一年用下来没有掉线丢包的情况。国内机适合与备案域名一起建站使用。带宽很小,图片资源使用CDN加速或海外机提供。 规格 CPU - 2核 内存 - 2GB 系统盘 - SSD云硬盘…...

消息称苹果或在明年推出搭载M3芯片的MacBook产品
近日据 DigiTimes 发布的博文,苹果公司计划在 2024 年推出搭载 M3 芯片的 MacBook 产品。然而,关于这款新产品的发布日期仍存在争议。虽然一些爆料认为苹果可能会在今年发布这款产品,但也有一些爆料认为发布时间会推迟到 2024 年。根据各项报…...

Generalizable NeRF in ICCV‘23
文章目录 前置知识Generalizable《Enhancing NeRF akin to Enhancing LLMs: Generalizable NeRF Transformer with Mixture-of-View-Experts》《WaveNeRF: Wavelet-based Generalizable Neural Radiance Fields》NeO 360: Neural Fields for Sparse View Synthesis of Outdoor …...
Unity2017适配安卓12
测试版本为Unity2017.4.25f1 1.在自定义AndroidManifest.xml(位于Assets\Plugins\Android\)中添加android:exported"true" <?xml version"1.0" encoding"utf-8"?> <manifestxmlns:android"http://schema…...

ios UI 基础开发一
目录 第一节:基础库 第二节:弹出模拟器的键盘 第三节:模拟器回到桌面 第四节:Viewcontroller 与 View 的关系 第五节:快捷键 第六节:键盘召回 第七节:启动流程xcode介绍 第八节…...
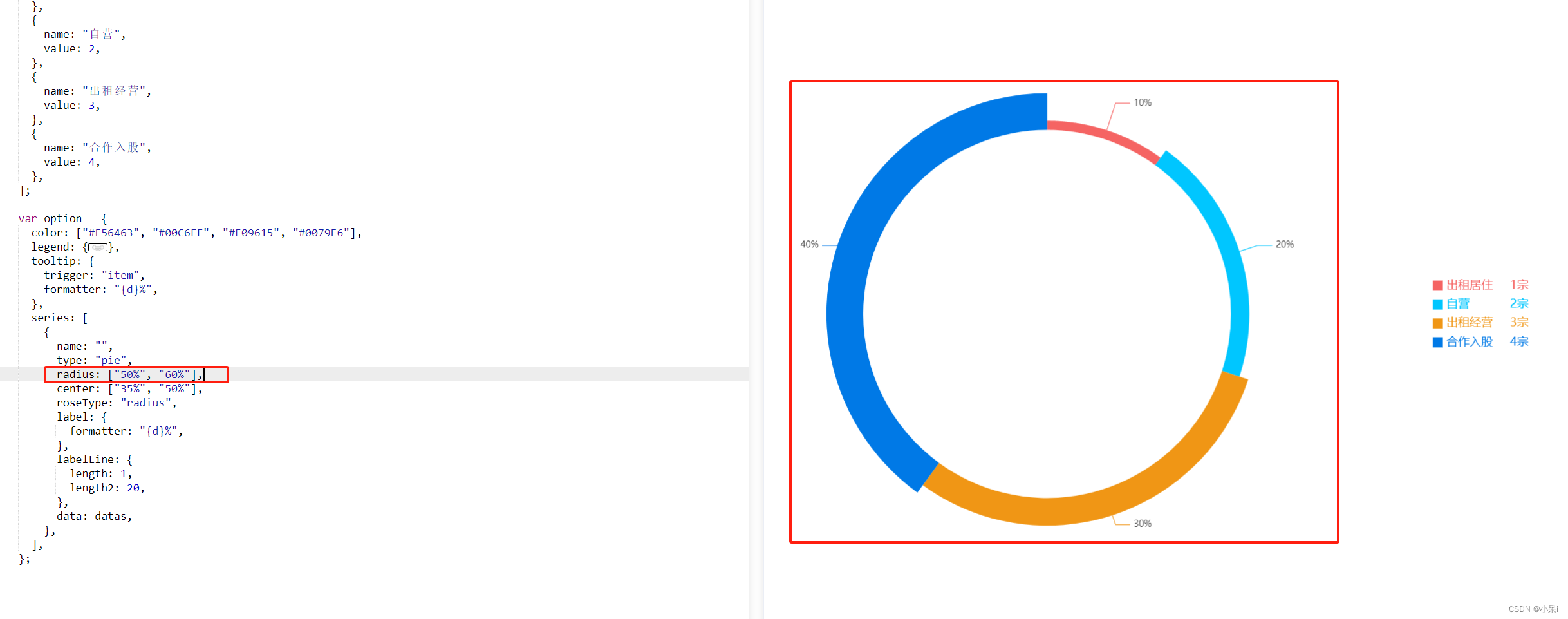
echarts一些配置项的使用
前言:我是自己最近写项目用到的,我做个整理; 一. 基本使用 1.具有大小(宽高)的div ,id唯一; 例如: <div id"crewEchart"></div> 2.在项目中引入: import * as echarts from "echarts"; 3.写一个关于他的方法,在mounted的时候调用: moun…...
(安全解析函数,解析yaml)(防止yaml文件中包含恶意代码))
python yaml库:safe_load()(安全解析函数,解析yaml)(防止yaml文件中包含恶意代码)
文章目录 Python YAML: 使用 safe_load 进行安全解析什么是 safe_load?如何使用 safe_load?为什么选择 safe_load 而非 load? Python YAML: 使用 safe_load 进行安全解析 YAML (YAML Ain’t Markup Language) 是一种人类可读的数据序列化标准。它被广泛用于配置文件、多语言…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
