一篇文章带你用动态规划解决股票购买时机问题
动态规划的解题步骤可以分为以下五步,大家先好好记住
1.创建dp数组以及明确dp数组下标的含义 2.制定递推公式 3.初始化 4.遍历顺序 5.验证结果
股票购买时机问题的解题核心思路
当天的收益是根据前一天持有股票还是不持有股票的状态决定的
那么很自然的我们就想到了使用动态规划的思想来解决问题,接下来就根据动态规划以及解题的核心思想来解决 股票购买时机问题
121. 买卖股票的最佳时机
根据题意: 某一天 买入这只股票,并选择在 未来的某一个不同的日子
也就是说我们只用买卖股票一次即可 那么根据动态规划的解题步骤以及核心思想我们一步步分析
1.创建dp数组以及明确dp数组下标的含义
//0 表示持不有股票的状态 1表示持有股票的状态
int[][] dp = new int[prices.length][2];2.制定递推公式
//持有的状态 - 要么是保持持有状态 要么是今天买入股票
dp[i][0] = Math.max(dp[i-1][0],-prices[i]);
//不持有的状态 - 要么是保持不持有状态 要么是今天卖出股票
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);3.初始化
dp[0][0] = -prices[0];
dp[0][1] = 0;4.遍历顺序
//从前往后遍历- 由于我们是从 i = 1 开始遍历的所以是prices[i-1]
for(int i = 1;i < dp.length;i++){//持有dp[i][0] = Math.max(dp[i-1][0],-prices[i]);//不持有 dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);
}5.验证
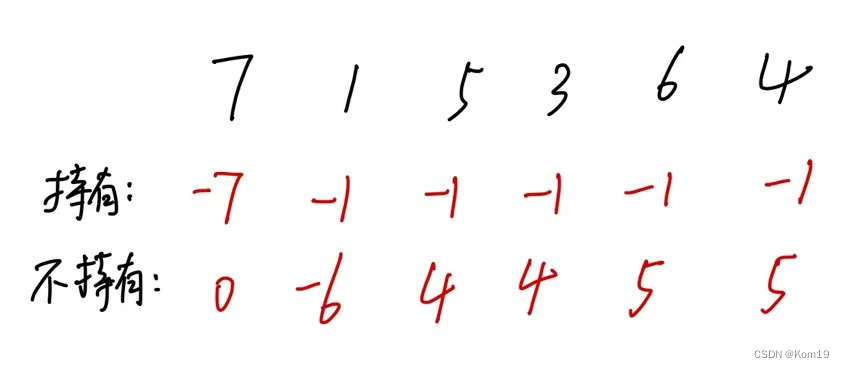
最后贴上完整代码
public int maxProfit(int[] prices) {int len = prices.length;//dp数组下标的含义是当日持有股票和不持有股票的最大利润int[][] dp = new int[len][2];//递推公式//dp[i][0] 表示持有股票 dp[i][1] 表示不持有股票//dp[i][0] = Math.max(dp[i-1][0],dp[i-1][0] - prices[i]);//dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);//初始化dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1;i < dp.length;i++){//持有dp[i][0] = Math.max(dp[i-1][0],-prices[i]);//不持有dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);}return Math.max(dp[len-1][0],dp[len-1][1]);}122. 买卖股票的最佳时机 II
本题遇上一题最大的不同就是可以多次买卖股票了,大题思路和上一题是差不多的
所以我们只需要在 2.指定递推公式 这里修改一下即可
由于可以多次买卖股票了,那么在今天买入股票这个步骤就需要参考昨天不持有股票的状态了
这就是和上一题不同的地方,上一题由于只需要买入一次,所以不用参考任何状态
那么只需要简单的进行修改即可
for(int i = 1;i < dp.length;i++){//持有dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1] - prices[i]);//不持有dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);}123. 买卖股票的最佳时机 III
本题说了只能购买两次股票那么难度就增加了,但是核心思路“当天的收益是根据是前一天持有股票还是不持有股票的状态决定的”还是不变的
1.创建dp数组以及明确dp数组下标的含义
int len = prices.length;
//dp数组的下标的含义是当日持有股票或者不持有股票获得的最大收益
//0~1表示第一次持有股票 2~3表示第二次持有股票
int[][] dp = new int[len + 1][4];2.制定递推公式
第一次持有是第一题的递推公式思路(只能买卖股票一次)
第二次持有是第二题的思路,因为此时买卖股票需要结合上一次买卖股票的状态来决定(多次买卖股票)
结合上两题的思想我们得到递推公式
//第一次持有
dp[i][0] = Math.max(dp[i-1][0], -prices[i]);
//第一次不持有
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);
//第二次持有
dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1] - prices[i]);
//第二次不持有
dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2] + prices[i]);3.初始化
//第一次持有
dp[0][0] = -prices[0];
//第一次不持有
dp[0][1] = 0;
//第二次持有
dp[0][2] = -prices[0];
//第二次不持有
dp[0][3] = 0;4.遍历顺序
从前往后
for(int i = 1;i < dp.length;i++){dp[i][0] = Math.max(dp[i-1][0], -prices[i-1]);dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1] - prices[i]);dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2] + prices[i]);
}最后完整代码如下
public int maxProfit(int[] prices) {int len = prices.length;int[][] dp = new int[len][4];//第一次持有dp[0][0] = -prices[0];//第一次不持有dp[0][1] = 0;//第二次持有dp[0][2] = -prices[0];//第二次不持有dp[0][3] = 0;for(int i = 1;i < dp.length;i++){dp[i][0] = Math.max(dp[i-1][0], -prices[i]);dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1] - prices[i]);dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2] + prices[i]);}return dp[len-1][3];}188. 买卖股票的最佳时机 IV
别被吓着!这题实际上和上一题是一模一样的!
区别就在于这一题是购买K次,而K则是题目随机分配的
但思路还是一样的!
那么怎么来解决掉0~K次的各个状态呢?答案也很简单!使用for循环
比如初始化的时候我们可以使用for循环来进行初始化
//初始化for(int i = 1;i < k*2 + 1;i += 2){//规定奇数是持有的状态 偶数是不持有的状态dp[0][i] = -prices[0];}当我们制定递推公式的时候也是使用for循环来帮助我们实现的
//遍历顺序for(int i = 1;i < len;i++){for(int j = 0;j < 2*k - 1;j += 2){//持有dp[i][j+1] = Math.max(dp[i-1][j+1],dp[i-1][j] - prices[i]);//不持有dp[i][j+2] = Math.max(dp[i-1][j+2],dp[i-1][j+1] + prices[i]);}}你们看完可能会觉得很疑惑:不是说第一次持有股票不需要参考任何状态吗?那这个代码怎么解释
dp[i - 1][j] - prices[i];
注意我们在初始化的时候是从 i = 1 开始的 也就是说 第一次持有股票时的状态还是
dp[i][0] = - prices[i];
这样大家应该明白了吧
最后贴上完整的代码
class Solution {public int maxProfit(int k, int[] prices) {int len = prices.length;//dp数组int[][] dp = new int[len][k*2 + 1];//递推公式//持有操作 奇数//dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j] - price[i]);//不持有操作 偶数//dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j] + price[i]);//初始化for(int i = 1;i < k*2 + 1;i += 2){dp[0][i] = -prices[0];}//遍历顺序for(int i = 1;i < len;i++){for(int j = 0;j < 2*k - 1;j += 2){//持有dp[i][j+1] = Math.max(dp[i-1][j+1],dp[i-1][j] - prices[i]);//不持有dp[i][j+2] = Math.max(dp[i-1][j+2],dp[i-1][j+1] + prices[i]);}}//验证return dp[len - 1][k*2];}
}309. 买卖股票的最佳时机含冷冻期(老实说,这题是我觉得股票买卖时机里面最难的一题...)
想要解决这道难题首先我们得分析好状态,不然会越来越懵逼的
首先由持有状态 不持有状态(保持不持有状态,前一天是冷冻期状态) 冷冻期状态
我们先定义好dp数组
int[][] dp = new int[len][4];//1.持有股票(保持持有股票/今天买入股票) 2.保持不持有股票 3.今天卖出股票 4.处于冷冻期//持有dp[0][0] = -prices[0];//不持有dp[0][1] = 0;//今天卖出股票dp[0][2] = 0;//处于冷冻期 = 昨天卖出股票dp[0][3] = dp[0][2];持有状态可以由不持有状态和冷冻期状态进行推导,它可以是保持持有状态也可以是今天买入
dp[i][0] = Math.max(Math.max(dp[i-1][1],dp[i-1][3]) - prices[i],dp[i-1][0]);那么不持有状态可以由保持不持有状态和前一天是冷冻期进行推导
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][3]);今天卖出股票直接由持有状态进行推导
dp[i][2] = dp[i-1][0] + prices[i];冷冻期状态实际上就是保持了昨天卖出股票的状态
dp[i][3] = dp[i-1][2];状态推导完了剩下也就简单了,直接上代码
class Solution {public int maxProfit(int[] prices) {int len = prices.length;int[][] dp = new int[len][4];//1.持有股票(保持持有股票/今天买入股票) 2.保持不持有股票 3.今天卖出股票 4.处于冷冻期//持有dp[0][0] = -prices[0];//不持有dp[0][1] = 0;//今天卖出股票dp[0][2] = 0;//处于冷冻期 = 昨天卖出股票dp[0][3] = dp[0][2];for(int i = 1;i < len;i++){//持有股票dp[i][0] = Math.max(Math.max(dp[i-1][1],dp[i-1][3]) - prices[i],dp[i-1][0]);//保持不持有股票dp[i][1] = Math.max(dp[i-1][1],dp[i-1][3]);//今天卖出股票dp[i][2] = dp[i-1][0] + prices[i];//处于冷冻期dp[i][3] = dp[i-1][2];}return Math.max(dp[len-1][1],Math.max(dp[len-1][2],dp[len-1][3]));}
}714. 买卖股票的最佳时机含手续费
本题实际上只用在第二题的基础上扣除手续费就好了只需要修改这一段代码即可
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i] - fee);股票买卖时机问题我们只需要把握一点就是把 持有和不持有 两个状态分析好,题目就会变得很简单
相关文章:
一篇文章带你用动态规划解决股票购买时机问题
动态规划的解题步骤可以分为以下五步,大家先好好记住 1.创建dp数组以及明确dp数组下标的含义 2.制定递推公式 3.初始化 4.遍历顺序 5.验证结果 股票购买时机问题的解题核心思路 当天的收益是根据前一天持有股票还是不持有股票的状态决定的 那么很自然的我们就想…...
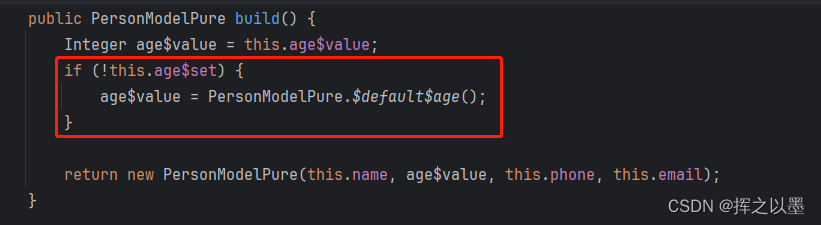
【设计模式】使用建造者模式组装对象并加入自定义校验
文章目录 1.前言1.1.创建对象时的痛点 2.建造者模式2.1 被建造类准备2.2.建造者类实现2.3.构建对象测试2.4.使用lombok简化建造者2.5.lombok简化建造者的缺陷 3.总结 1.前言 在我刚入行不久的时候就听说过建造者模式这种设计模式,当时只知道是用来组装对象…...

简单聊聊低代码
在数字经济迅速发展的背景下,越来越多的企业开始建立健全业务系统、应用、借助数字化工具提升管理效率,驱动业务发展,促进业绩增长。在这一过程中,和许多新技术一样,低代码(Low-code)开发被推上…...
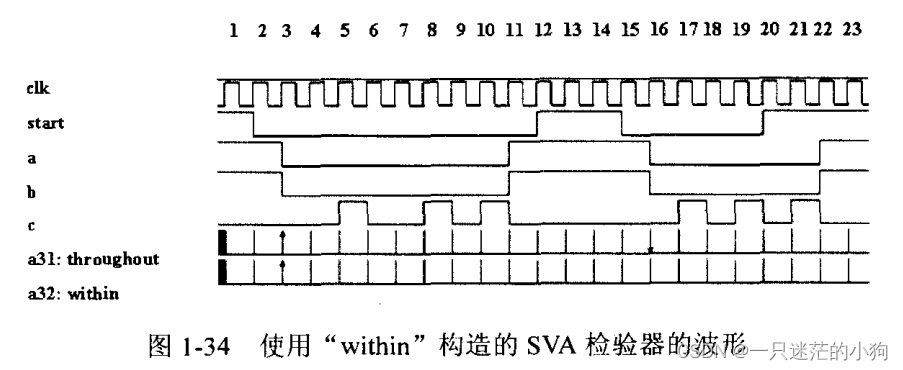
SystemVerilog Assertions应用指南 第一章(1.27章节 “within”运算符)
“ within”构造允许在一个序列中定义另一个序列。 seq1 within seq2 这表示seq1在seq2的开始到结束的范围内发生,且序列seq2的开始匹配点必须在seq1的开始匹配点之前发生,序列seq1的结束匹配点必须在seq2的结束匹配点之前结束。属性p32检查序列s32a在信号“ start”的上升沿和…...

2023年09月 C/C++(七级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 Python编程(1~6级)全部真题・点这里 第1题:红与黑 有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上,只能向相邻的黑色瓷砖移动。请写一个程序,计算你总共能够到达多少块黑色的瓷砖。 时间限…...
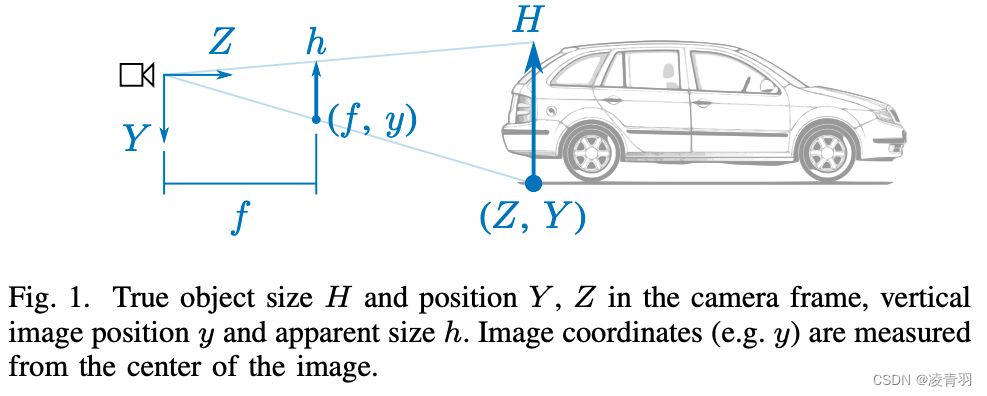
[Mono Depth/3DOD]单目3D检测基础
1. 数据增强 图像放缩和裁剪后,相机内参要做相应变化 import random def random_scale(image, calib, scale_range(0.8, 1.2)):scale random.uniform(*scale_range)width, height image.sizeimage image.resize((int(width * scale), int(height * scale)))cal…...
:PID namespace)
【Docker 内核详解】namespace 资源隔离(三):PID namespace
namespace 资源隔离(三):PID namespace 1.PID namespace 中的 init 进程2.信号与 init 进程3.挂载 proc 文件系统4.unshare() 和 setns() PID namespace 隔离非常实用,它对进程 PID 重新标号,即两个不同 namespace 下的…...

1600*C. Game On Leaves(博弈游戏树)
Problem - 1363C - Codeforces 解析: 我们将目标结点 x 当作树的根,显然,到当 x 的度为 1 的时候,此时行动的人胜利。 我们假设现在的情况为,只剩余三个点,再选择任意一个点,则对方获胜。但是两…...
Apache Ant的安装
介绍 Apache Ant是一个Java库和一个 命令行工具,可以用来构建Java应用。Ant提供了许多内置的任务(tasks),可以编译、组装、测试、运行Java应用。Ant也可以构建非Java应用,例如C、C应用。 Ant非常灵活,没有…...

考研:数学二例题--∞−∞和0⋅∞型极限
前言 本文只是例题,建议先参考具体如何做这类型例题。请到主文章中参考:https://blog.csdn.net/grd_java/article/details/132246630 ∞ − ∞ 和 0 ⋅ ∞ \infin - \infin 和 0\infin ∞−∞和0⋅∞ 例题 例1: lim x → ∞ x 2 x 2 −…...

C++算法:图中的最短环
题目 现有一个含 n 个顶点的 双向 图,每个顶点按从 0 到 n - 1 标记。图中的边由二维整数数组 edges 表示,其中 edges[i] [ui, vi] 表示顶点 ui 和 vi 之间存在一条边。每对顶点最多通过一条边连接,并且不存在与自身相连的顶点。 返回图中 …...

C++学习——类其实也是一种作用域
以下内容源于C语言中文网的学习与整理,非原创,如有侵权请告知删除。 其实也是一种作用域,每个类都会定义它自己的作用域。在类的作用域之外,普通的成员只能通过对象(可以是对象本身,也可以是对象指针或对象…...

Seata入门系列【4】undo_log、global_table、branch_table、lock_table字段及作用详解
1 客户端 1.1 undo_log 在AT模式中,需要在参与全局事务的数据库中,添加一个undo_log表,建表语句如下: SET NAMES utf8mb4; SET FOREIGN_KEY_CHECKS 0;-- ---------------------------- -- Table structure for undo_log -- --…...

虚幻引擎:数据表格的C++常用API
1.将数据表格中的所有数据存到一个数组中 //参数1 // 错误提示 //参数2 // 存储的数组 TArray<FKeyInfoHeader*> array; KeyInfoDT->GetAllRows<FKeyInfoHeader>(TEXT("错误"),array); 2.获取表格中所有的行名称 TArray<FName>array; …...
)
Java日期格式化(DateFormat类和SimpleDateFormat类)
格式化日期表示将日期/时间格式转换为预先定义的日期/时间格式。例如将日期“Fri May 18 15:46:24 CST2016” 格式转换为 “2016-5-18 15:46:24 星期五”的格式。 在 java 中,可以使用 DateFormat 类和 SimpleDateFormat 类来格式化日期,下面详细介绍这两…...
centos 7 lamp owncloud
OwnCloud是一款开源的云存储软件,基于PHP的自建网盘。基本上是私人使用,没有用户注册功能,但是有用户添加功能,你可以无限制地添加用户,OwnCloud支持多个平台(windows,MAC,Android&a…...

屏幕亮度调节保护您的眼睛
官方下载地址: 安果移动 视频演示:屏幕亮度调节-保护您的眼睛_哔哩哔哩_bilibili 嗨,亲爱的用户,你是否有过这样的体验:夜晚安静的时刻,想要在抖音上看看热门的舞蹈、在快手上发现生活的 趣味、或是在哔…...

CentOS Linux下CMake二进制文件安装并使用Visual Studio调试
cmake安装——二进制安装(很简单,推荐!!) 1)下载二进制包。首先就是官网下载二进制安装包(我们是64位系统,就下载对应的包),这里。 例如:在/home/DOWNLOAD目录下执行,即下载二进制…...

ASP.net相关目录,相关配置文件和.后缀名解释
App_Data:用于存储应用程序的数据文件,例如数据库文件或其他本地文件。 App_Start:包含应用程序的启动配置文件,例如路由配置、日志配置等。 Content:存放应用程序的静态资源文件,如 CSS、JavaScript、图…...
一键批量转换,轻松将TS视频转为MP4视频,实现更广泛的播放和分享!
在享受精彩视频内容的同时,有时我们可能会面临一个问题:某些视频格式可能不太适合我们的播放设备或分享平台。特别是TS格式的视频,在一些情况下可能无法直接播放或上传。但是不用担心,因为我们为您提供了一款强大的视频剪辑工具&a…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
