136.只出现一次的数字
136. 只出现一次的数字 - 力扣(LeetCode)
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入:nums = [2,2,1] 输出:1
示例 2 :
输入:nums = [4,1,2,1,2] 输出:4
示例 3 :
输入:nums = [1] 输出:1
提示:
1 <= nums.length <= 3 * 104-3 * 104 <= nums[i] <= 3 * 104- 除了某个元素只出现一次以外,其余每个元素均出现两次。
思路
利用异或运算;借鉴文章:http://t.csdnimg.cn/oydZq
完整代码
class Solution {public int singleNumber(int[] nums) {int result = nums[0];if(nums.length>1){for(int i=1;i<nums.length;i++){result = result^nums[i];}}return result;}
}相关文章:

136.只出现一次的数字
136. 只出现一次的数字 - 力扣(LeetCode) 给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 你必须设计并实现线性时间复杂度的算法来解决此问题,且…...

mysql中遇到查询字段的别名与函数冲突问题
比如以下哎,我查询城市行业数量排名 select City, DENSE_RANK() over(ORDER BY COUNT(Id) DESC) rank, COUNT(Id) num,IndustrySubGroupName from base_companyinfo WHERE IndustrySubGroupName工业机器人 GROUP BY City 上面使用 DENSE_RANK() 函数来计算排名&am…...

直播获奖
题目描述 NOI2130 即将举行。为了增加观赏性, CCF 决定逐一评出每个选手的成 绩,并直播即时的获奖分数线。本次竞赛的获奖率为 𝑤% ,即当前排名前 𝑤% 的选手的最低成绩就是即时的分数线。 更具体地,…...
选择适合自身业务的HTTP代理有哪些因素决定?
相信对很多爬虫工作者和数据采集的企业来说,如何选购适合自己业务的HTTP代理是一个特别特别困扰的选题,市面上那么多HTTP代理厂商,好像这家有这些缺点,转头又看到另外一家的缺点,要找一家心仪的仿佛大海捞针。今天我们…...

1.3 do...while实现1+...100 for实现1+...100
思路:两个变量,一个变量存储数据之和,一个变量实现自增就行 do...while int i, s;i 1;s 0;do{s 1;i;} while (i < 100);cout << s << endl; for int i, j0;for (i 1; i < 100; i){j 1;}cout << j << …...

react数据管理之setState与Props
react数据管理之setState与Props setState调用原理 setState 是 React 中用于更新组件状态(state)的方法。它的调用原理可以分为以下几个步骤: 状态的改变:当调用 setState 时,React 会将新的状态对象与当前状态对象…...

如何保护我们的网络安全
保护网络安全是至关重要的,尤其是在今天的数字化时代。以下是一些保护网络安全的基本步骤: 1、使用强密码:使用包含字母、数字和特殊字符的复杂密码。不要在多个网站上重复使用相同的密码。定期更改密码。 2、启用双因素认证 (2FA)ÿ…...
springboot 制造装备物联及生产管理ERP系统
springboot 制造装备物联及生产管理ERP系统 liu1113625581...

Google zxing 生成带logo的二维码图片
环境准备 开发环境 JDK 1.8SpringBoot2.2.1Maven 3.2 开发工具 IntelliJ IDEAsmartGitNavicat15 添加maven配置 <dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.4.0</version> </…...

使用Python计算平面多边形间最短距离
要计算平面多边形间的最短距离,首先需要导入Excel表格中的多边形数据,然后使用GJK(Gilbert-Johnson-Keerthi)算法来判断两个多边形是否重叠。如果两个多边形不重叠,可以计算它们之间的最短距离。 以下是一个基本的Pyt…...

【Python】Python语言基础(中)
第十章 Python的数据类型 基本数据类型 数字 整数 整数就是整数 浮点数 在编程中,小数都称之为浮点数 浮点数的精度问题 print(0.1 0.2) --------------- 0.30000000000000004 1.可以通过round()函数来控制小数点后位数 round(a b),则表示…...

观察者模式、订阅者发布者模式、vtk中的观察者模式
文章目录 什么是观察者模式vtk是如何实现的观察者模式.AddObserver什么时候使用观察者模式?什么使用订阅发布者模式?观察者模式的实现订阅发布者的实现总结知识补充: 什么是观察者模式 用于在对象之间建立一对多的依赖关系,当一个对象的状态发生变化时…...

关于element-ui中,页面上有多个el-table并通过v-if、v-else等控制是否显示时,type=selection勾选框失效或不显示的问题
刚开始是勾选框那一列直接空了什么都不显示,搜索了一下说是给el-table标签增加id,加了之后是显示了,但是点击任何选框都会直接取消全部选中效果,翻了半天源码也没发现到底是哪里事件冲突了还是怎么回事,烦了࿰…...

Stewart六自由度正解、逆解计算-C#和Matlab程序
目录 一、Stewart并联六自由度正解计算 (一)概况 (二)Matlab正解计算 1、参考程序一 2、参考程序二 (三)C#程序正解计算 1、工程下载链接 2、正解运行计算 (四)正程…...

C语言 驼峰命名法和下划线命名法
在C语言中,变量命名遵循以下规则: 变量名只能由字母、数字和下划线组成。变量名必须以字母或下划线开头。变量名不能使用C语言中的关键字。变量名中不能出现连续的两个下划线。变量名区分大小写,例如,count和Count被视为两个不同…...
-hive压缩)
大数据学习(8)-hive压缩
&&大数据学习&& 🔥系列专栏: 👑哲学语录: 承认自己的无知,乃是开启智慧的大门 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝支持一下博>主哦&#x…...
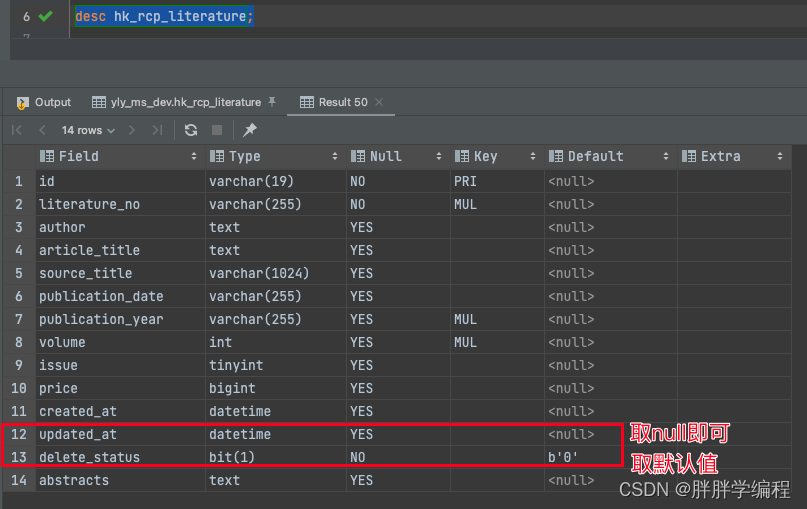
[sqoop]hive导入mysql,其中mysql的列存在默认值列
一、思路 直接在hive表中去掉有默认值的了列,在sqoop导入时,指定非默认值列即可, 二、具体 mysql的表 hive的表 create table dwd.dwd_hk_rcp_literature(id string,literature_no string,authors string,article_title string,source_title string…...
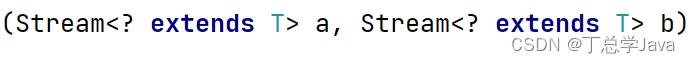
Stream流中的常用方法(forEach,filter,map,count,limit,skip,concat)和Stream流的特点
1、forEach方法 该方法接收一个Consumer接口是一个 消费型 的函数式接口,可以传递Lambda表达式,消费数据用来遍历流中的数据,是一个 终结 方法,遍历 之后就不能继续调用Stream流中的其他方法 package com.csdn.stream; import jav…...

2023大联盟2比赛总结
比赛链接 反思 T1 奇怪的贪心和构造题一直是我的软肋部分 T2 简单题 T3 也不难 T4 套路没学过,感觉还是太菜了 题解 A 考虑先给图随便染色,然后调整 因为每个点的度数为 3 3 3,所以如果有 x → u → v x\to u\to v x→u→v 的颜…...
Flutter笔记:电商中文货币显示插件Money Display
Flutter笔记 电商中文货币显示插件 Money Display 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/1338…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
