2023大联盟2比赛总结
比赛链接
反思
T1
奇怪的贪心和构造题一直是我的软肋部分
T2
简单题
T3
也不难
T4
套路没学过,感觉还是太菜了
题解
A
考虑先给图随便染色,然后调整
因为每个点的度数为 3 3 3,所以如果有 x → u → v x\to u\to v x→u→v 的颜色全部相同,那么修改 u u u 的颜色一定能使 u u u 符合条件,然后就用队列存储调整的点,一直调整即可
估算一下时间复杂度是 O ( n ) O(n) O(n) 级别的,肯定不会调整很多次
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
const int N=200100;
int col[N],deg[N];
bool inq[N];
vector<int> G[N];
queue<int> que;
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
void upd(int x){deg[x]=0;for(int v:G[x]) if(col[v]==col[x]) deg[x]++;if(deg[x]>=2&&!inq[x]) inq[x]=1,que.push(x);
}
void work(){int n=read(),m=read();while(!que.empty()) que.pop();for(int i=1;i<=n;i++) G[i].clear(),inq[i]=0;for(int i=1;i<=m;i++){int x=read(),y=read();G[x].pb(y),G[y].pb(x);}for(int i=1;i<=n;i++) col[i]=0;for(int i=1;i<=n;i++) upd(i);int cnt=0;while(!que.empty()){int u=que.front();que.pop();inq[u]=0;if(deg[u]<2) continue;cnt++;if(cnt>m) break;col[u]^=1;upd(u);for(int v:G[u]) upd(v);}if(!que.empty()) puts("GG");else{for(int i=1;i<=n;i++) printf("%d ",col[i]);puts("");return;}
}
int main(){freopen("classical.in","r",stdin);freopen("classical.out","w",stdout);int T=read();while(T--) work();fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}B
感觉这才是本场比赛的签到题
可以发现操作类似冒泡排序,然后手玩一下样例发现答案为逆序对数
无解情况判一下奇偶性即可
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
#include <bits/stdc++.h>
#define lowbit(x) x&-x
using namespace std;
typedef long long LL;
typedef pair<int,int> pii;
const int N=1000100;
int n,p[N],tr[N],a[2][N],b[2][N];
pii pos[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
void add(int x){ for(;x<=n;x+=lowbit(x)) tr[x]++;}
int ask(int x){int res=0;for(;x;x-=lowbit(x)) res+=tr[x];return res;
}
int main(){freopen("rotate.in","r",stdin);freopen("rotate.out","w",stdout);n=read();for(int i=1;i<=n;i++) a[0][i]=read();for(int i=1;i<=n;i++) a[1][i]=read();for(int i=1;i<=n;i++) b[0][i]=read();for(int i=1;i<=n;i++) b[1][i]=read();for(int i=1;i<=n;i++) pos[b[0][i]]={0,i},pos[b[1][i]]={1,i};//check -1for(int i=1;i<=n;i++){int x=a[0][i];if(!pos[x].first&&pos[x].second==i) continue;if(((pos[x].first-i)&1)!=(pos[x].second&1)){ puts("-1");exit(0);}}for(int i=1;i<=n;i++) p[i]=pos[a[0][i]].second;LL ans=0;for(int i=n;i>=1;i--) ans+=ask(p[i]),add(p[i]);printf("%lld\n",ans);fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}C
这道题最重要的想法是:分治
考虑对于左上角 ( x 1 , y 1 ) (x_1,y_1) (x1,y1),右下角 ( x 2 , y 2 ) (x_2,y_2) (x2,y2) 的矩形求出覆盖矩形内所有 1 1 1 的方案数,这可以枚举行和列的分割线,递归下去求解
时间复杂度 O ( n 5 ) O(n^5) O(n5),需要加一些剪枝就能卡过去了
#include <bits/stdc++.h>
using namespace std;
bool Mbe;
const int N=65;
int n,s[N][N],f[N][N][N][N];
bool a[N][N];
char str[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
inline void chkmin(int &x,int y){ if(y<x) x=y;}
int calc(int lx,int ly,int rx,int ry){ return s[rx][ry]-s[lx-1][ry]-s[rx][ly-1]+s[lx-1][ly-1];}
int solve(int lx,int ly,int rx,int ry){auto &t=f[lx][ly][rx][ry];if(t!=-1) return t;if(!calc(lx,ly,rx,ry)){ t=0;return 0;}if(rx-lx+1<ry-ly+1){bool flg=1;for(int i=ly;i<=ry;i++) if(!calc(lx,i,rx,i)){ flg=0;break;}if(flg){ t=ry-ly+1;return t;}}else{bool flg=1;for(int i=lx;i<=rx;i++) if(!calc(i,ly,i,ry)){ flg=0;break;}if(flg){ t=rx-lx+1;return t;}}t=max(rx-lx+1,ry-ly+1);//枚举分割线for(int i=lx;i<rx;i++){int tmp=solve(lx,ly,i,ry);if(tmp<t) chkmin(t,tmp+solve(i+1,ly,rx,ry));}for(int j=ly;j<ry;j++){int tmp=solve(lx,ly,rx,j);if(tmp<t) chkmin(t,tmp+solve(lx,j+1,rx,ry));}return t;
}
bool Med;
int main(){freopen("detection.in","r",stdin);freopen("detection.out","w",stdout);// fprintf(stderr,"%.3lf MB\n",(&Mbe-&Med)/1048576.0);n=read();for(int i=1;i<=n;i++){scanf("%s",str+1);for(int j=1;j<=n;j++) a[i][j]=str[j]=='T';}for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];memset(f,-1,sizeof(f));printf("%d\n",solve(1,1,n,n));fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}D
感觉是套路题
首先 O ( n 2 ) O(n^2) O(n2) 的树形 d p dp dp 是好做的
考虑 k = 1 k=1 k=1 的部分分,这一部分有一个经典的想法:考虑答案即为 ∏ s i z 每一个联通快 \prod siz_{每一个联通快} ∏siz每一个联通快,直接做仍是 O ( n 2 ) O(n^2) O(n2) 的,重要:考虑它的组合意义,即为在每个连通块内选一个点的方案数,这个可以令 f i , 0 / 1 f_{i,0/1} fi,0/1 表示 i i i 所在的连通块是否选过点的方案和,时间复杂度 O ( n ) O(n) O(n),期望得分 50 p t s 50pts 50pts
考虑一步转化是: s k = ∑ i = 0 k { k i } s i ‾ = ∑ i = 0 k { k i } ( s i ) i ! s^k=\sum\limits_{i=0}^{k}{k\brace i}s^{\underline{i}}=\sum\limits_{i=0}^{k}{k\brace i}\binom{s}{i}i! sk=i=0∑k{ik}si=i=0∑k{ik}(is)i!
考虑 { k i } k\brace i {ik} 和 i ! i! i! 都是好算的,主要是 ( s i ) \binom{s}{i} (is),这个可以根据组合意义用 d p dp dp 计算,即令 f i , j f_{i,j} fi,j 为 i i i 的联通快内选 j j j 个点的方案和,但 j ≤ k j\le k j≤k,所以时间复杂度 O ( n k ) O(nk) O(nk)
#include <bits/stdc++.h>
using namespace std;
const int N=100100,K=110,P=1e9+7;
int n,m,fac[K],siz[N],t[K];
int e[N],ne[N],h[N],idx;
int stir2[K][K];
int f[N][K],g[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
void add(int x,int y){ e[idx]=y,ne[idx]=h[x],h[x]=idx++;}
void dfs(int u){f[u][0]=f[u][1]=1,siz[u]=1;for(int i=h[u];~i;i=ne[i]){int v=e[i];dfs(v);for(int j=0;j<=min(m,siz[u]+siz[v]);j++) t[j]=0;for(int j=0;j<=siz[u];j++) t[j]=1ll*f[u][j]*g[v]%P;// for(int j=0;j<=m;j++) cout<<t[j]<<' ';cout<<'\n';for(int j=0;j<=siz[u];j++) for(int k=0;k<=min(siz[v],m-j);k++)t[j+k]=(t[j+k]+1ll*f[u][j]*f[v][k])%P;siz[u]=min(m,siz[u]+siz[v]);for(int j=0;j<=siz[u];j++) f[u][j]=t[j];}for(int i=0;i<=m;i++) g[u]=(g[u]+1ll*stir2[m][i]*fac[i]%P*f[u][i])%P;
}
int main(){freopen("calc.in","r",stdin);freopen("calc.out","w",stdout);n=read(),m=read();stir2[0][0]=1;for(int i=1;i<=m;i++)for(int j=1;j<=i;j++) stir2[i][j]=(stir2[i-1][j-1]+1ll*j*stir2[i-1][j])%P;fac[0]=1;for(int i=1;i<=m;i++) fac[i]=1ll*fac[i-1]*i%P;memset(h,-1,sizeof(h));for(int i=2;i<=n;i++) add(read(),i);dfs(1);printf("%d\n",g[1]);fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}相关文章:

2023大联盟2比赛总结
比赛链接 反思 T1 奇怪的贪心和构造题一直是我的软肋部分 T2 简单题 T3 也不难 T4 套路没学过,感觉还是太菜了 题解 A 考虑先给图随便染色,然后调整 因为每个点的度数为 3 3 3,所以如果有 x → u → v x\to u\to v x→u→v 的颜…...
Flutter笔记:电商中文货币显示插件Money Display
Flutter笔记 电商中文货币显示插件 Money Display 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/1338…...
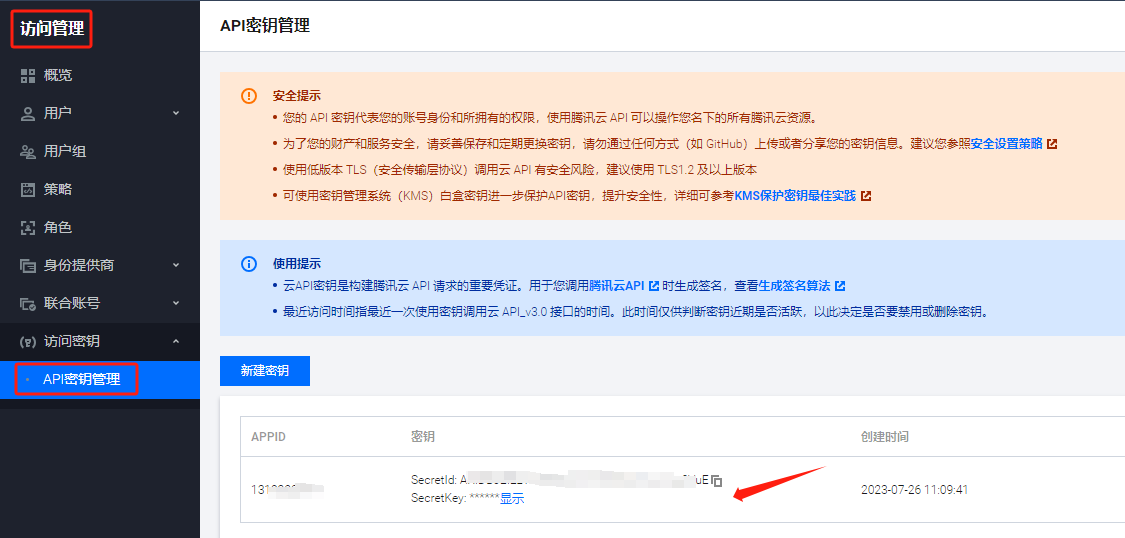
腾讯云上创建 对象存储cos
1. 登录腾讯云, 找到对象存储cos 2. 创建存储桶 3. 获取4个配置参数 桶名称 / 地域secretId / secretKey...
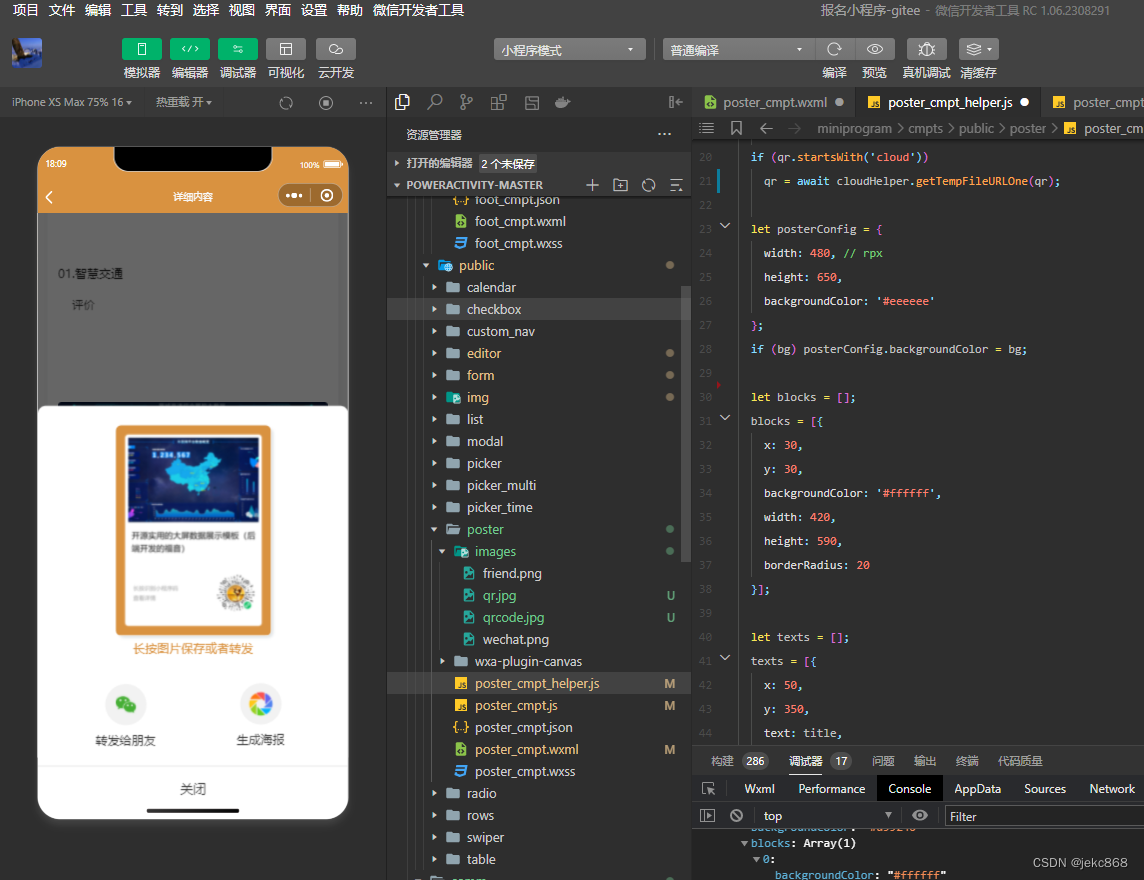
微信小程序生成海报
效果: js1: const cloudHelper = require(../../../helper/cloud_helper.js);async function config1({cover,title,desc,qr,bg = }) {var qr1 ="images/qr.png"var qr2 ="https://636c-cloud1-0gu29f2j63906b7e-1319556650.tcb.qcloud.la/activitycomm/setu…...
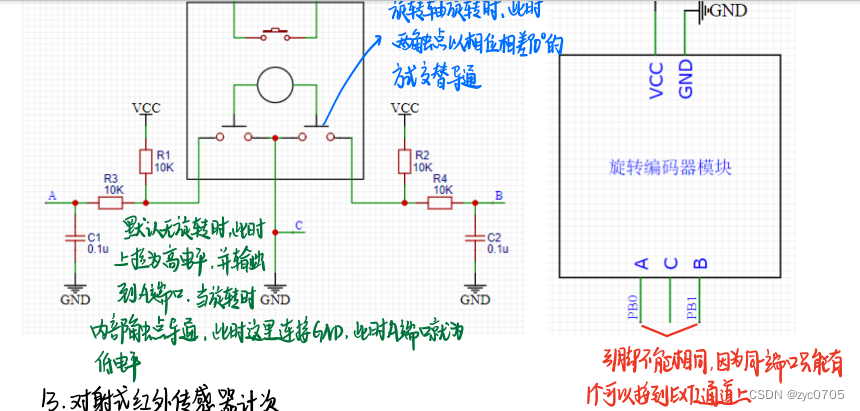
stm32学习笔记:EXIT中断
1、中断系统 中断系统是管理和执行中断的逻辑结构,外部中断是众多能产生中断的外设之一。 1.中断: 在主程序运行过程中,出现了特定的中断触发条件 (中断源,如对于外部中断来说可以是引脚发生了电平跳变,对于定时器来…...

css 块元素、行内元素、行内块元素相互转换
在HTML和CSS中,元素可以分为三类:块级元素(Block-level Elements)、内联元素(Inline Elements)和内联块级元素(Inline-block Elements)。 块级元素(Block-level Elements…...

【JUC】多线程基础概述
文章目录 1. 一锁二并三程2. 用户线程和守护线程 1. 一锁二并三程 一锁:synchronized 二并: 并发:一台处理器“同时”处理多个任务,同一时刻只有一个事件发生并行:多台处理器同时处理多个任务,同一时刻多个处理器分…...

Git 回退代码的两种方法对比
Git 回退代码版本 在项目的开发中,有时候还是会出现,一些误提交了一些代码,这时候就会想撤回提交的代码,在Git中有两种方法可以使用,现在通过对比方法比较这两种方法的区别,分别适用于哪些情况?…...
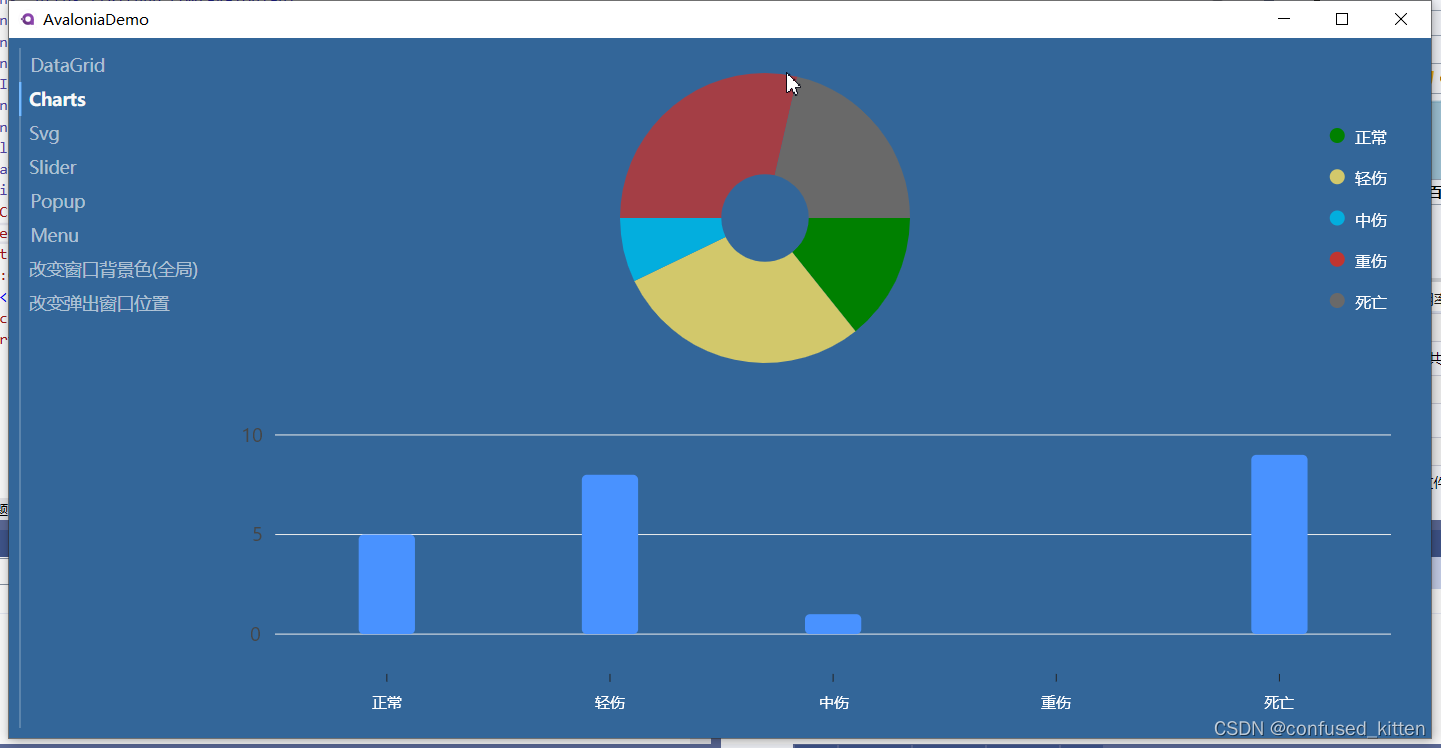
Avalonia常用小控件Charts
1.项目下载地址:https://gitee.com/confusedkitten/avalonia-demo 2.UI库Semi.Avalonia,项目地址 https://github.com/irihitech/Semi.Avalonia 3.Charts库,LiveChartsCore.SkiaSharpView.Avalonia,Nuget获取只有预览库&#x…...

【Hugging Face】管理 huggingface_hub 缓存系统
摘要 这篇文档介绍了Hugging Face Hub的缓存系统。该系统旨在提供一个中央缓存,以便不同版本的文件可以被下载和缓存。缓存系统将文件组织成模型、数据集和空间等不同的目录,每个目录包含特定类型的文件。系统确保如果文件已经下载并更新,除非明确要求,否则不会再次下载。…...

Python学习基础笔记六十六——对象的方法
我们已经学习到的对象类型: 整数类型的对象 字符串类型的对象 列表类型的对象 元组类型的对象 对象通常都有属于自己的方法(method) 调用对象的方法和调用函数差不多,只要在前面加上所属对象的一个点。 var1 [1, 2, 3,4, 5,…...

建立一个新的高阶数学教授模式,知其然,知其用,知其之所以然,知其所以然
1. 传统常用的模式 概念,性质,定理,定理证明,定理应用; 这个学习模式挺好的,但是定理证明过程往往很冗长,而且不易记忆,也就是说,即使推导了定理,初学者也记…...

AtCoder ABC324G 启发式合并
题意 传送门 AtCoder ABC324G Generate Arrays 题解 逆则操作顺序考虑,可以看作至多 n n n 个联通分量不断合并的过程,此时使用启发式合并,即规模较小的连通分量向规模较大的连通分量合并,以单个元素合并为基本运算࿰…...
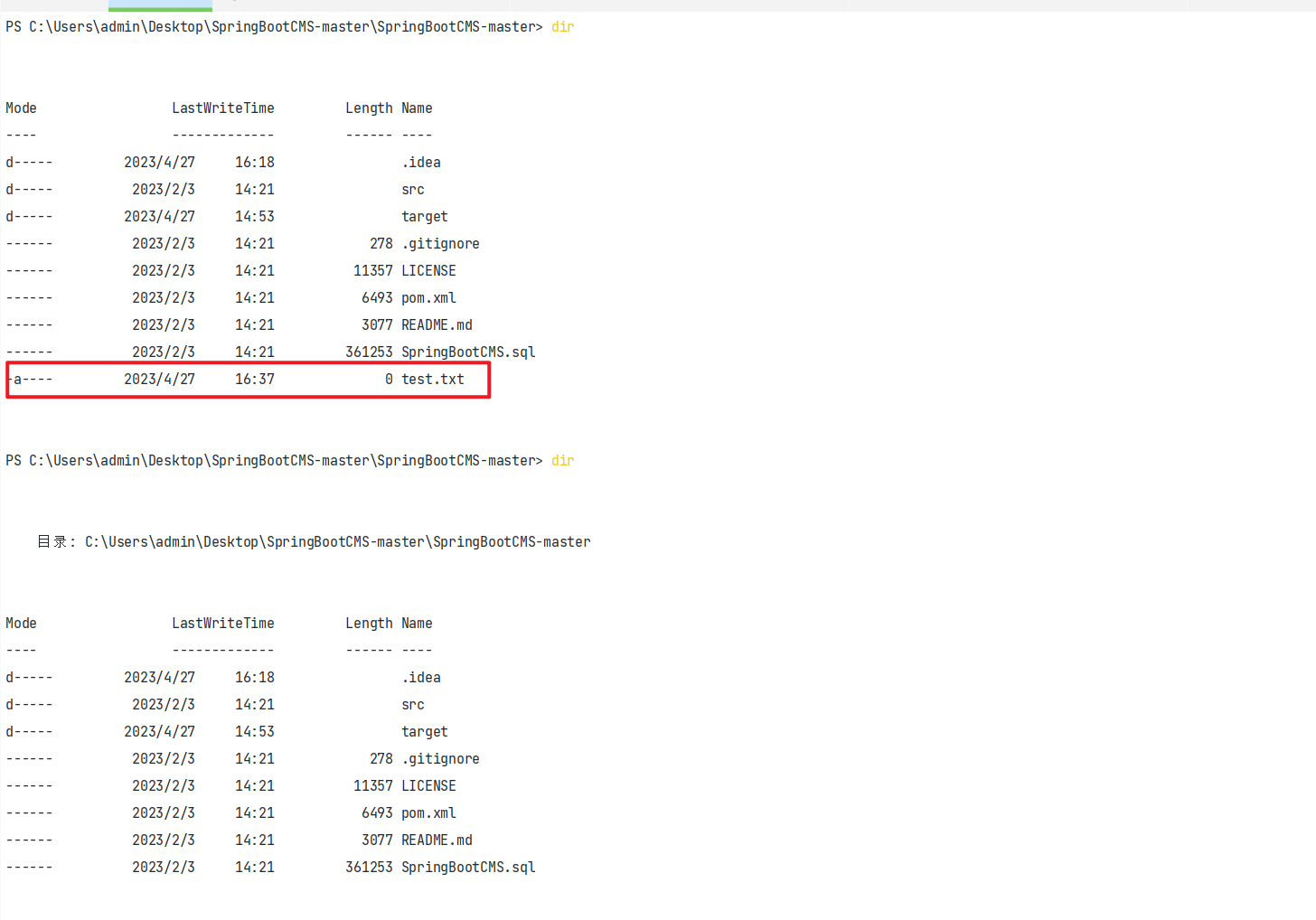
SpringBootCMS漏洞复现分析
SpringBootCMS,极速开发,动态添加字段,自定义标签,动态创建数据库表并crud数据,数据库备份、还原,动态添加站点(多站点功能),一键生成模板代码,让您轻松打造自己的独立网站ÿ…...
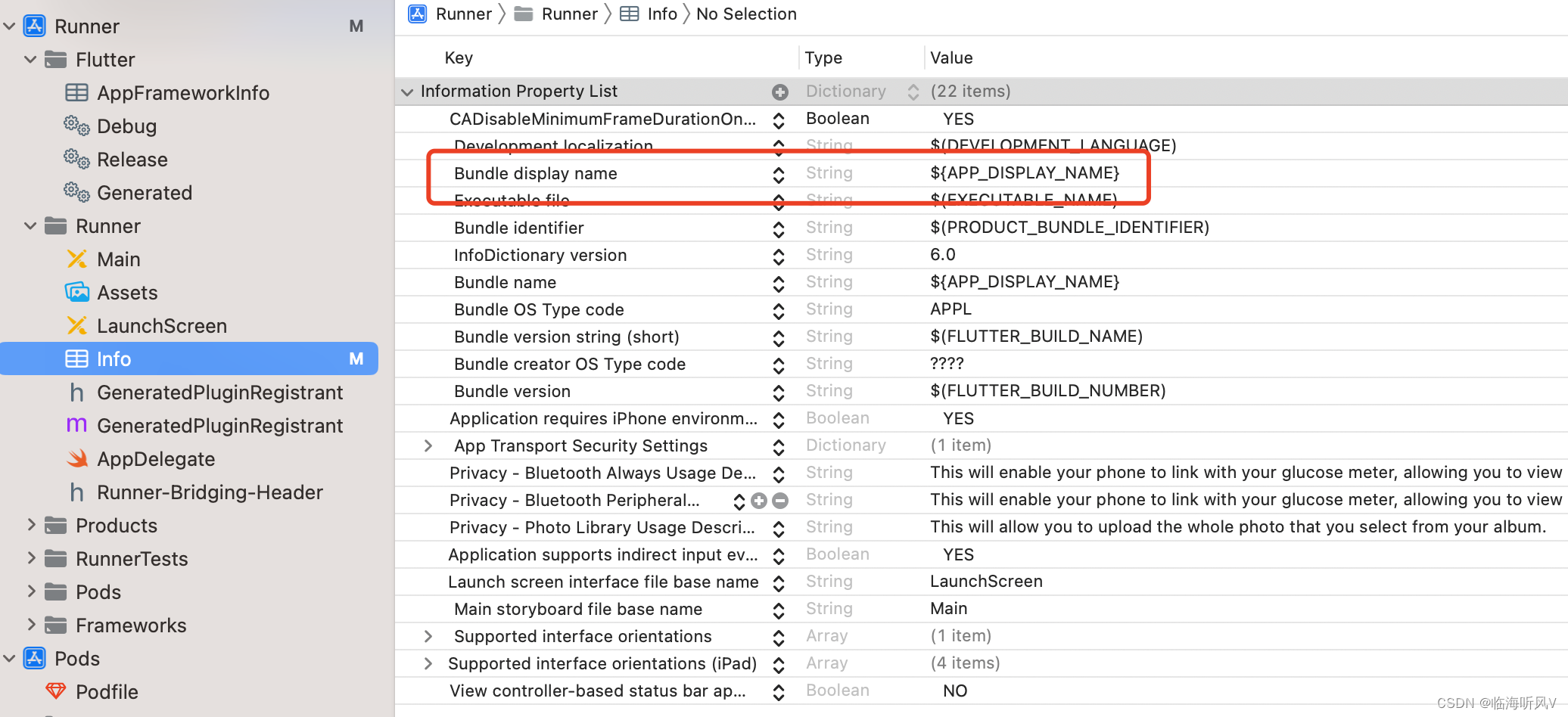
iOS- flutter flavor 多环境Configurations配置
一、点击PROJECT的Runner,选择Info选项,在Configurations下方的号添加不同环境的配置,如下图: 二、选择TAGETS的Runner项目,选择Build Settings选项,在输入框输入package,为不同环境配置相应的…...
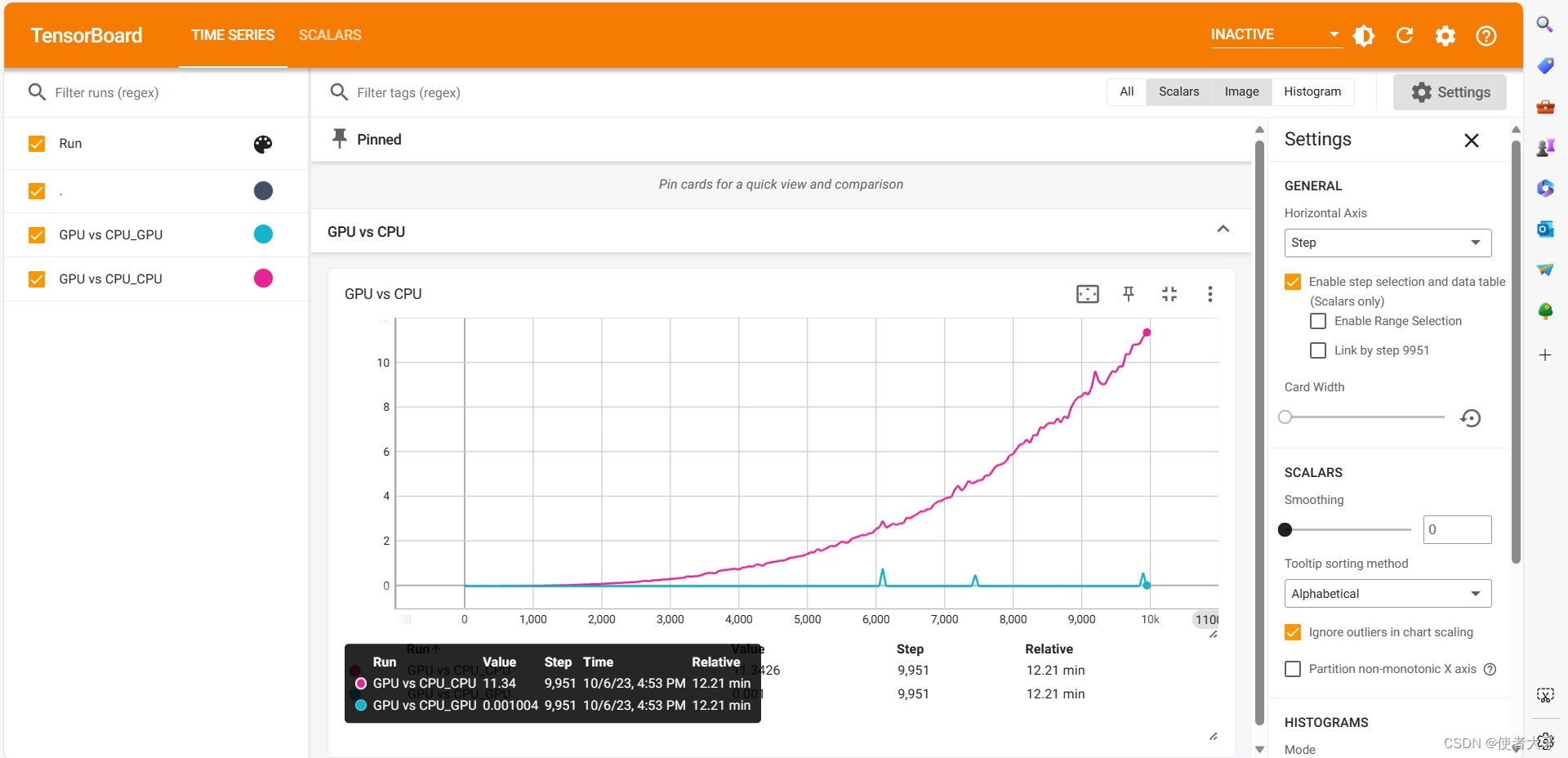
【PyTorchTensorBoard实战】GPU与CPU的计算速度对比(附代码)
0. 前言 按照国际惯例,首先声明:本文只是我自己学习的理解,虽然参考了他人的宝贵见解,但是内容可能存在不准确的地方。如果发现文中错误,希望批评指正,共同进步。 本文基于PyTorch通过tensor点积所需要的时…...

npm 常用指令总结
1. 初始化包 一个存放了代码的文件夹,如果里面有 package.json 文件,则可以把这个文件夹称之为包。 npm init -y 注意: 由于包名不能有中文,不能有大写,不能和未来要下载的包重名. 所以我们快速初始化包时,我们的文件夹也不能违反前面说的规则.(因为默认会将文件夹的名称,作…...

布朗大学发现GPT-4存在新问题,可通过非常见语言绕过限制
🦉 AI新闻 🚀 布朗大学发现GPT-4存在新漏洞,可通过非常见语言绕过限制 摘要:布朗大学计算机科学研究人员发现了OpenAI的GPT-4存在新漏洞,利用不太常见的语言如祖鲁语和盖尔语可以绕过各种限制。研究人员测试了GPT-4对…...

ESP32网络编程-TCP客户端数据传输
TCP客户端数据传输 文章目录 TCP客户端数据传输1、IP/TCP简单介绍2、软件准备3、硬件准备4、TCP客户端实现本文将详细介绍在Arduino开发环境中,实现一个ESP32 TCP客户端,从而达到与TCP服务器数据交换的目标。 1、IP/TCP简单介绍 Internet 协议(IP)是 Internet 的地址系统,…...

微信小程序入门级
目录 一.什么是小程序? 二.小程序可以干什么? 三.入门使用 3.1. 注册 3.2. 安装 3.3.创建项目 3.4.项目结构 3.5.应用 好啦今天就到这里了,希望能帮到你哦!!! 一.什么是小程序? 微信小程…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
