Git 回退代码的两种方法对比
Git 回退代码版本
在项目的开发中,有时候还是会出现,一些误提交了一些代码,这时候就会想撤回提交的代码,在Git中有两种方法可以使用,现在通过对比方法比较这两种方法的区别,分别适用于哪些情况?
在Git中回退代码,经常使用revert或者reset来做,这两种操作都可以用来回退,但是却有比较大的区别,一般比较安全性的还是使用revert来做,revert是撤回对应的提交记录,然后再提交撤回记录,只是会在Git历史里多一些记录,reset的操作是直接将git历史回退到对应的版本,之后的记录全都撤回了,所以除非情况允许,不然不建议使用
git revert操作
git revert:revert撤回的意思,意思是撤回提交的代码,然后在Git的所有提交记录后面新增一次提交,不会撤回之前的代码,所以是很安全性的撤回方法,不过就会新增一次撤回记录
git revert使用方法:
# 撤回指定版本,后面可以加一个git记录id
git revert [版本ID]
# 撤回上个版本的提交
git revert HEAD^
# 撤回上上个版本提交
git revert HEAD^^
# 或者写成
git revert HEAD^2
如果有git客户端软件,比如smartgit,可以直接在ui界面操作
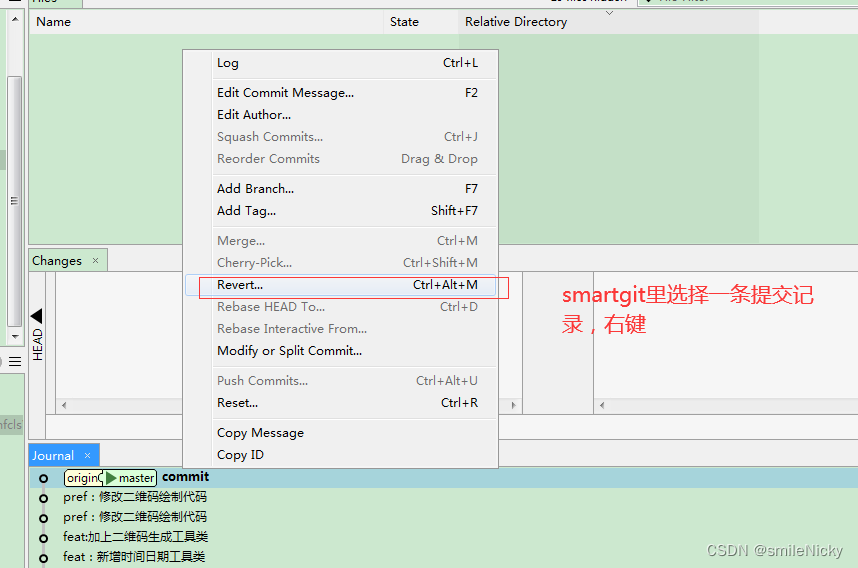
然后再提交上去,重新生成一次撤回记录

git reset 操作
git reset :reset,重置操作,是重置HEAD的位置,将代码重置到某个版本,某个版本之后的提交都会被清掉,所以不是很安全,非特殊情况,不建议使用
git reset的语法格式为:
git reset [--soft | --mixed | --hard] [HEAD]
-
–mixed(默认):默认的参数,将重置的更改留在工作区中
-
–soft:如果使用 --soft 参数,将重置的更改保存在暂存区
-
–hard参数:如果使用 --hard 参数,工作区和暂存区都不会保存记录,所以建议不要使用这种模式
OK,下面使用git命令实践一下
# 找到要回退的commit版本号,复制
git log
# 重置本地库版本回退
git reset --mixed [commitid]
# 同步到远端仓库,要写上分支名称
git push -f origin [branchName]
相关文章:

Git 回退代码的两种方法对比
Git 回退代码版本 在项目的开发中,有时候还是会出现,一些误提交了一些代码,这时候就会想撤回提交的代码,在Git中有两种方法可以使用,现在通过对比方法比较这两种方法的区别,分别适用于哪些情况?…...
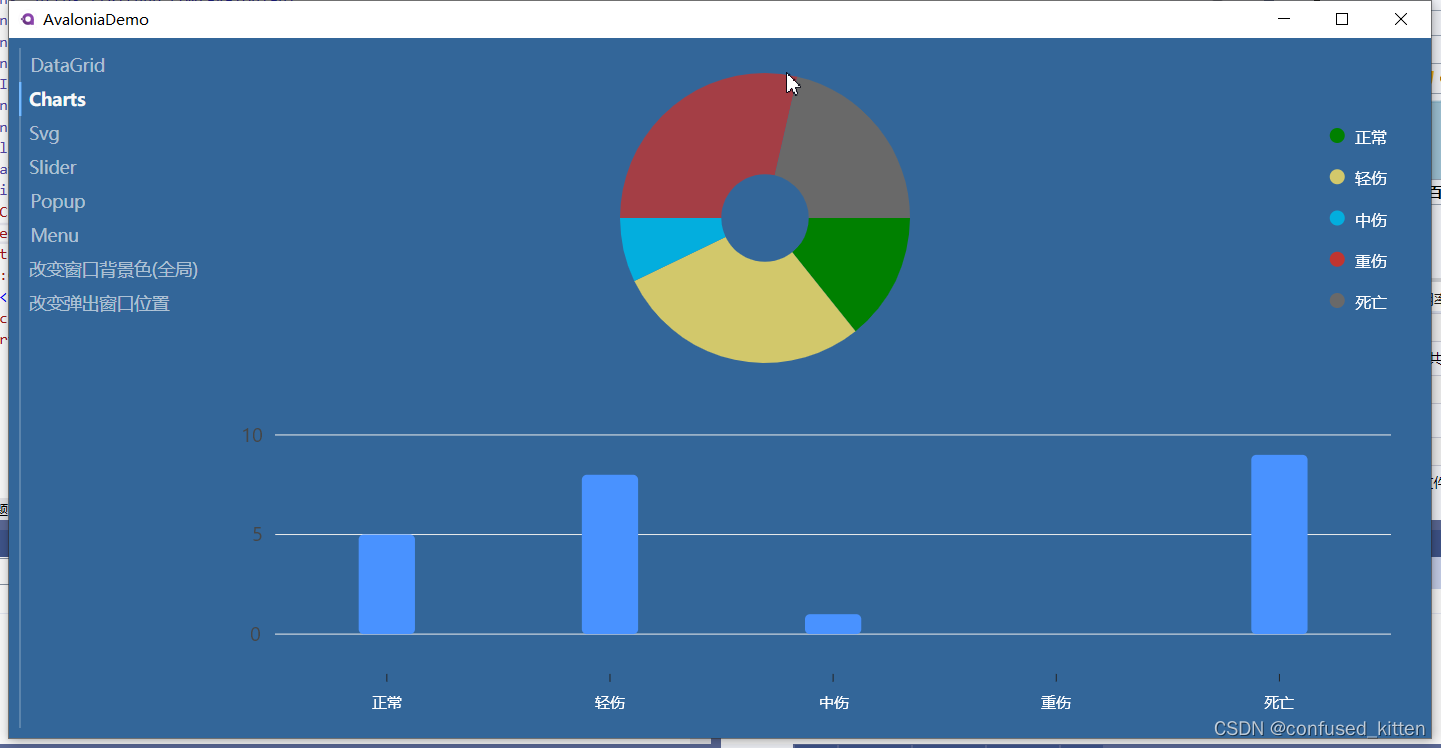
Avalonia常用小控件Charts
1.项目下载地址:https://gitee.com/confusedkitten/avalonia-demo 2.UI库Semi.Avalonia,项目地址 https://github.com/irihitech/Semi.Avalonia 3.Charts库,LiveChartsCore.SkiaSharpView.Avalonia,Nuget获取只有预览库&#x…...

【Hugging Face】管理 huggingface_hub 缓存系统
摘要 这篇文档介绍了Hugging Face Hub的缓存系统。该系统旨在提供一个中央缓存,以便不同版本的文件可以被下载和缓存。缓存系统将文件组织成模型、数据集和空间等不同的目录,每个目录包含特定类型的文件。系统确保如果文件已经下载并更新,除非明确要求,否则不会再次下载。…...

Python学习基础笔记六十六——对象的方法
我们已经学习到的对象类型: 整数类型的对象 字符串类型的对象 列表类型的对象 元组类型的对象 对象通常都有属于自己的方法(method) 调用对象的方法和调用函数差不多,只要在前面加上所属对象的一个点。 var1 [1, 2, 3,4, 5,…...

建立一个新的高阶数学教授模式,知其然,知其用,知其之所以然,知其所以然
1. 传统常用的模式 概念,性质,定理,定理证明,定理应用; 这个学习模式挺好的,但是定理证明过程往往很冗长,而且不易记忆,也就是说,即使推导了定理,初学者也记…...

AtCoder ABC324G 启发式合并
题意 传送门 AtCoder ABC324G Generate Arrays 题解 逆则操作顺序考虑,可以看作至多 n n n 个联通分量不断合并的过程,此时使用启发式合并,即规模较小的连通分量向规模较大的连通分量合并,以单个元素合并为基本运算࿰…...
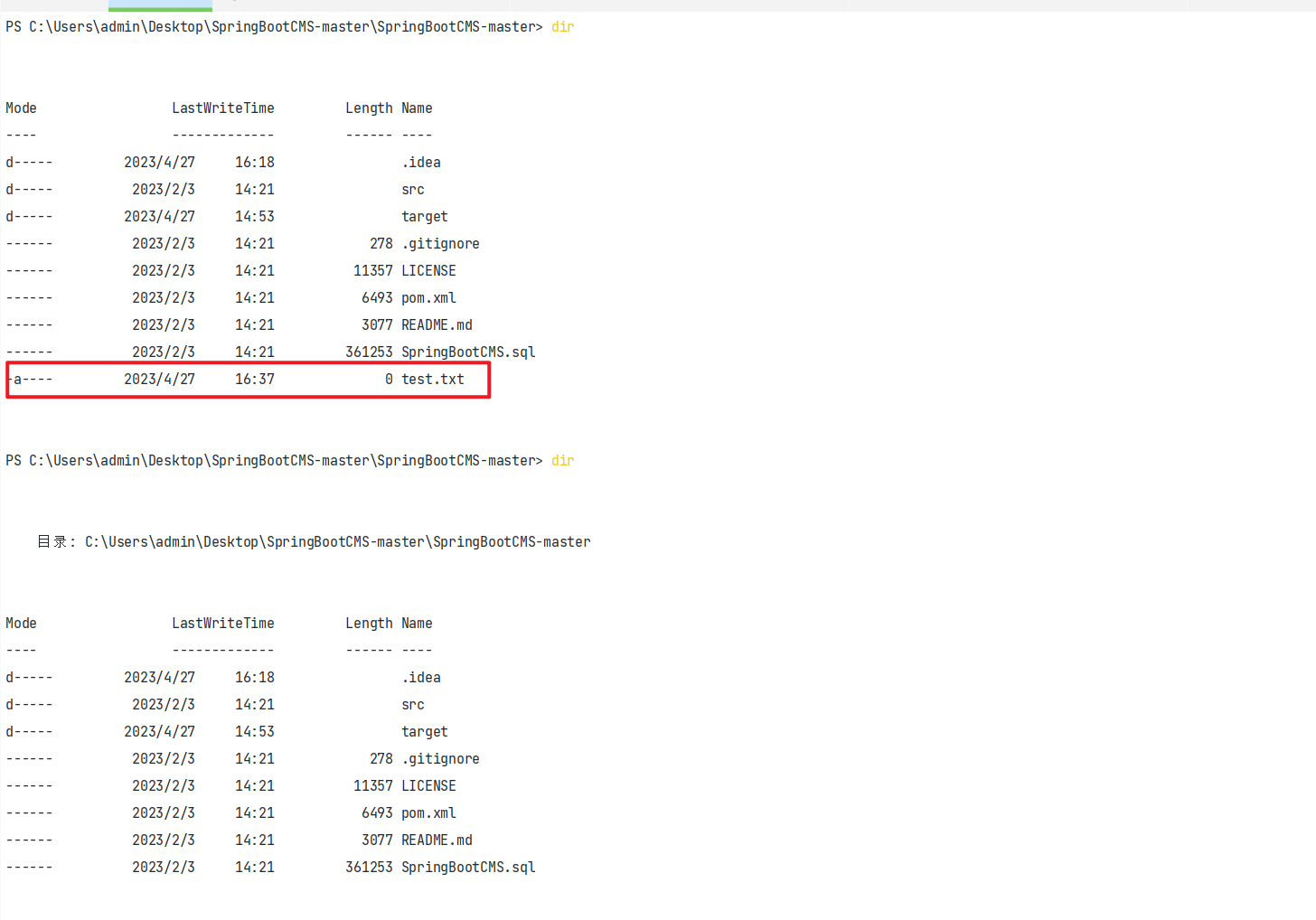
SpringBootCMS漏洞复现分析
SpringBootCMS,极速开发,动态添加字段,自定义标签,动态创建数据库表并crud数据,数据库备份、还原,动态添加站点(多站点功能),一键生成模板代码,让您轻松打造自己的独立网站ÿ…...
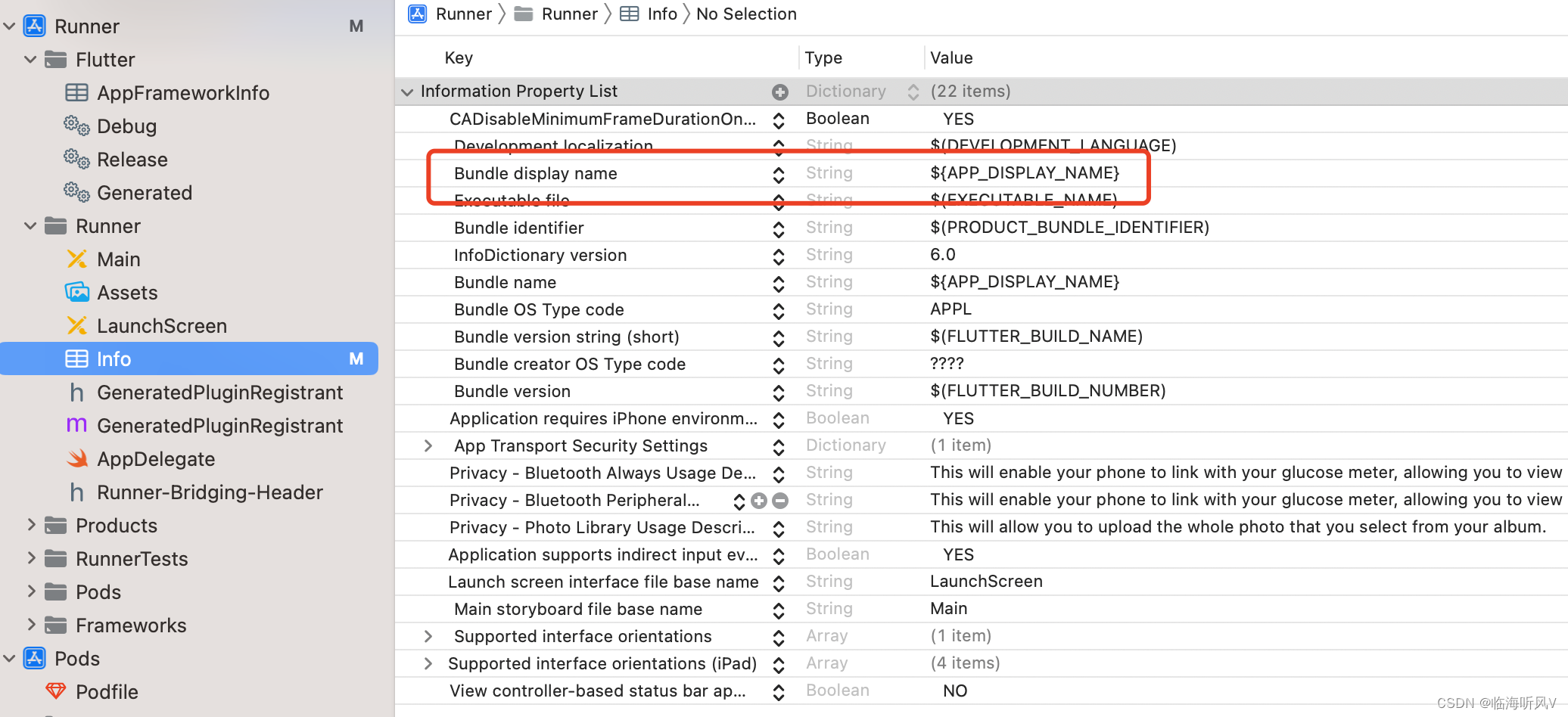
iOS- flutter flavor 多环境Configurations配置
一、点击PROJECT的Runner,选择Info选项,在Configurations下方的号添加不同环境的配置,如下图: 二、选择TAGETS的Runner项目,选择Build Settings选项,在输入框输入package,为不同环境配置相应的…...
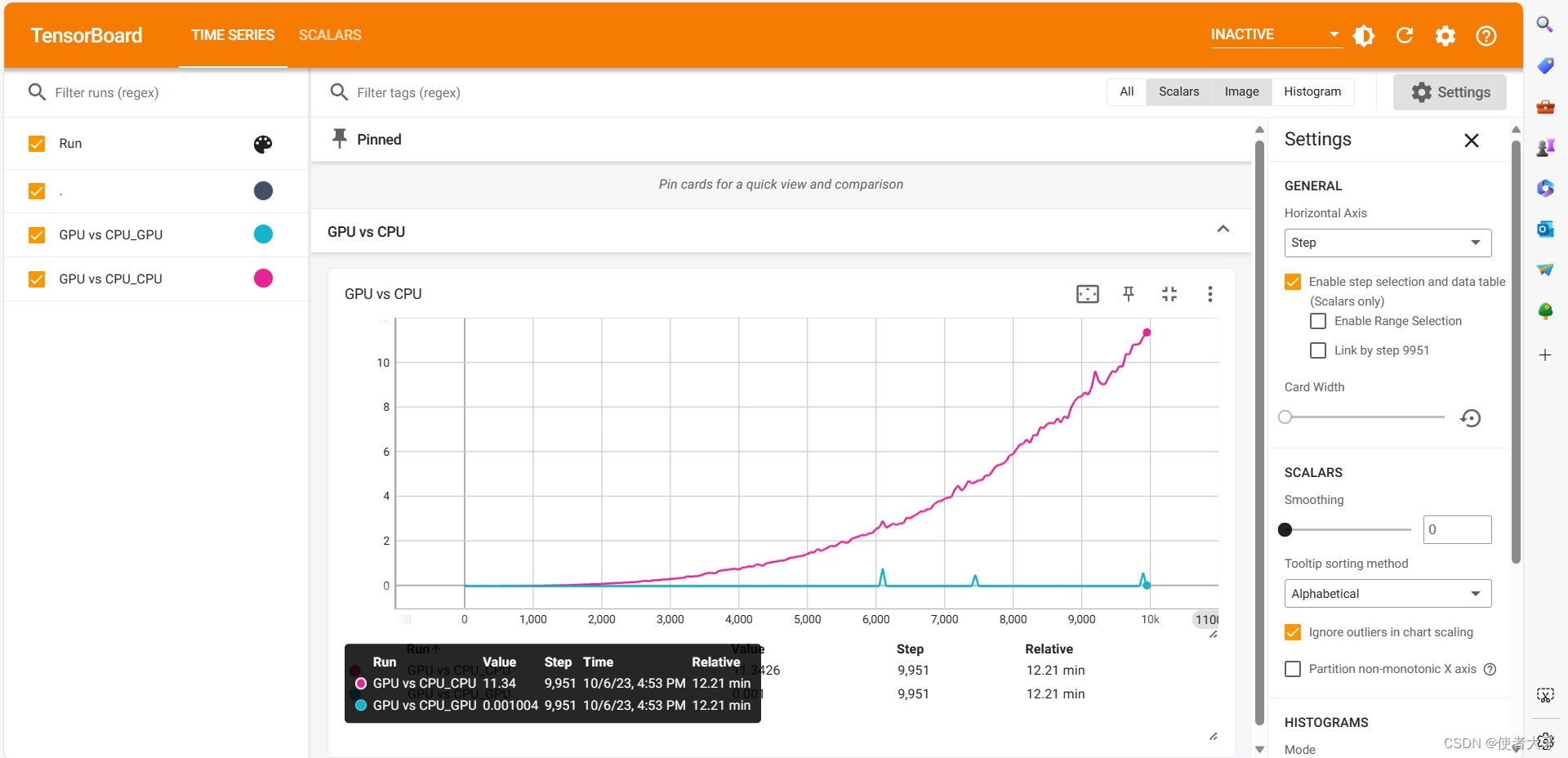
【PyTorchTensorBoard实战】GPU与CPU的计算速度对比(附代码)
0. 前言 按照国际惯例,首先声明:本文只是我自己学习的理解,虽然参考了他人的宝贵见解,但是内容可能存在不准确的地方。如果发现文中错误,希望批评指正,共同进步。 本文基于PyTorch通过tensor点积所需要的时…...

npm 常用指令总结
1. 初始化包 一个存放了代码的文件夹,如果里面有 package.json 文件,则可以把这个文件夹称之为包。 npm init -y 注意: 由于包名不能有中文,不能有大写,不能和未来要下载的包重名. 所以我们快速初始化包时,我们的文件夹也不能违反前面说的规则.(因为默认会将文件夹的名称,作…...

布朗大学发现GPT-4存在新问题,可通过非常见语言绕过限制
🦉 AI新闻 🚀 布朗大学发现GPT-4存在新漏洞,可通过非常见语言绕过限制 摘要:布朗大学计算机科学研究人员发现了OpenAI的GPT-4存在新漏洞,利用不太常见的语言如祖鲁语和盖尔语可以绕过各种限制。研究人员测试了GPT-4对…...

ESP32网络编程-TCP客户端数据传输
TCP客户端数据传输 文章目录 TCP客户端数据传输1、IP/TCP简单介绍2、软件准备3、硬件准备4、TCP客户端实现本文将详细介绍在Arduino开发环境中,实现一个ESP32 TCP客户端,从而达到与TCP服务器数据交换的目标。 1、IP/TCP简单介绍 Internet 协议(IP)是 Internet 的地址系统,…...

微信小程序入门级
目录 一.什么是小程序? 二.小程序可以干什么? 三.入门使用 3.1. 注册 3.2. 安装 3.3.创建项目 3.4.项目结构 3.5.应用 好啦今天就到这里了,希望能帮到你哦!!! 一.什么是小程序? 微信小程…...
)
博客文档续更(二)
十五、博客前台模块-个人信息 1. 接口分析 进入个人中心的时候需要能够查看当前用户信息。请求不需要参数 请求方式 请求地址 请求头 GET /user/userInfo 需要token请求头 响应格式 {"code":200,"data":{"avatar":"头像的网络地址…...

Centos切换yum源
Centos切换yum源 常用命令 #查看内核/操作系统/CPU信息 uname -a #查看yum源 yum list repolist all切换步骤 1.备份yum源文件 cp -a /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.bak2.下载新的CentOS-Base.repo文件到/etc/yum.repos.d/目录下 …...
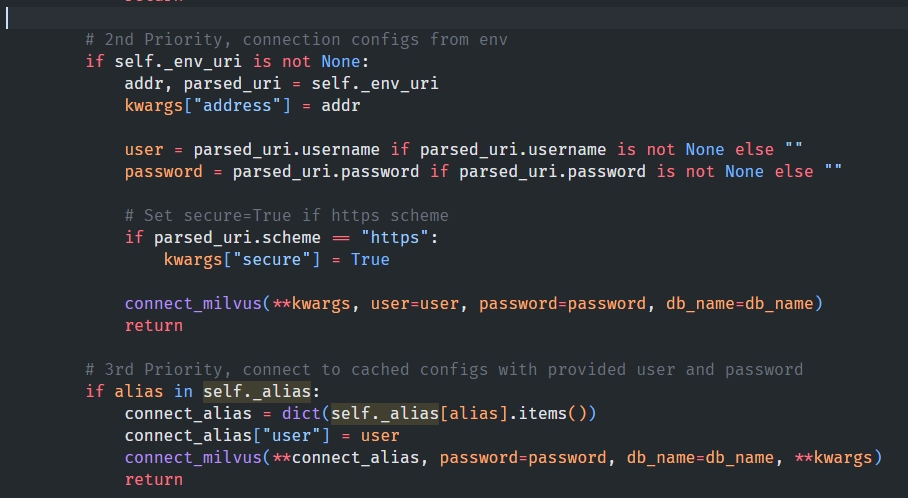
milvus和相似度检索
流程 milvus的使用流程是 创建collection -> 创建partition -> 创建索引(如果需要检索) -> 插入数据 -> 检索 这里以Python为例, 使用的milvus版本为2.3.x 首先按照库, python3 -m pip install pymilvus Connect from pymilvus import connections c…...
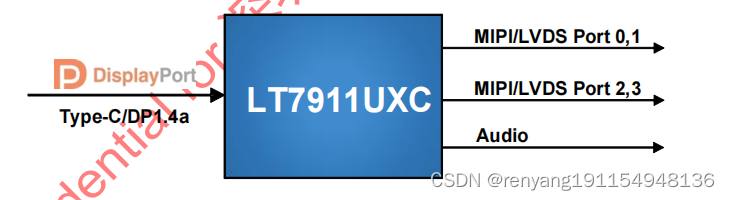
龙迅LT7911UXC 是一款高性能TYPE-C/DP/EDP转换四端口MIPI/LVDS的芯片,还支持图像处理
龙迅LT7911UXC 1.描述: LT7911UXC是一款用于VR/显示应用的高性能Type-C/DP1.4a到MIPI或LVDS芯片。HDCP RX作为 HDCP中继器的上游端,可以与其他芯片的HDCP TX协同工作,实现中继器的功能。对于DP1.4a 输入,LT7911UXC可以配置为1…...
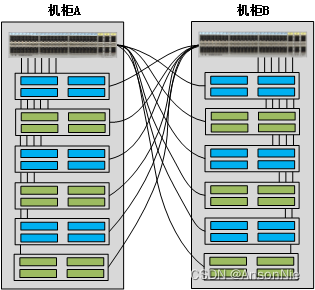
TOR(Top of Rack)
TOR TOR(Top of Rack)指的是在每个服务器机柜上部署1~2台交换机,服务器直接接入到本机柜的交换机上,实现服务器与交换机在机柜内的互联。虽然从字面上看,Top of Rack指的是“机柜顶部”,但实际T…...
使用asp.net core web api创建web后台,并连接和使用Sql Server数据库
前言:因为要写一个安卓端app,实现从服务器中获取电影数据,所以需要搭建服务端代码,之前学过C#,所以想用C#实现服务器段代码用于测试,本文使用C#语言,使用asp.net core web api组件搭建服务器端&…...
LaTeX 公式与表格绘制技巧
LaTeX 公式与绘图技巧公式基本可以分为 单一公式单一编号单一公式按行编号单一公式多个子编号单一公式部分子编号分段公式现在给出各自的代码单一公式单一编号 公式1:equationaligned\begin{equation}\begin{aligned}a&bc\\b&a2\\c&b-3\end{aligned}\en…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...
