亳州市的自然风光与旅游资源:欣赏安徽省中部的壮丽景色
亳州市是中国安徽省的一个地级市,位于该省的中部。
亳州市辖区包括谯城区、涡阳县、蒙城县和利辛县等地。亳州市拥有悠久的历史和丰富的文化遗产,同时也以其独特的自然风光而闻名。
首先,让我们来了解一下亳州的历史和景点。亳州的历史可以追溯到公元前770年左右,是中国历史文化名城之一。

亳州市区内有许多历史古迹,如亳州古城、亳州博物馆等,这些古迹见证了亳州的悠久历史和文化传统。
此外,亳州还拥有一些自然景点,如五龙口风景区、泗县湖等,这些景点以其壮丽的自然风光吸引了大量游客。
在亳州市的主要街道、商业中心和旅游景区,OLED透明拼接屏的应用表现出色。
这些拼接屏通过高清晰度和高对比度的图像显示,展示了亳州的城市形象和旅游资源。
OLED透明拼接屏的透明特性使得它们能够完美地融入城市环境中,不会给人带来视觉上的压迫感,反而增添了城市的美感和现代感。
同时,OLED透明拼接屏还通过信息发布和广告宣传,为市民和游客提供了实用的信息和优惠活动。
对于那些对OLED透明拼接屏感兴趣的个人和企业,他们可以选择代理、租赁或购买的方式来获得这些产品。
代理商可以帮助个人和企业寻找最适合他们需求的OLED透明拼接屏,并提供相应的技术支持和售后服务。
此外,对于一些短期活动或特殊需求,租赁OLED透明拼接屏也是一个灵活和经济的选择。
至于售价方面,OLED透明拼接屏的价格因品牌、规格和市场竞争等因素而有所差异,个人和企业可以根据自身预算进行选择。
总的来说,OLED透明拼接屏在亳州市的应用效果非常出色。
通过其高清晰度、高对比度和透明的特点,它们成功地提升了亳州的城市形象和旅游吸引力。
相信随着OLED透明拼接屏技术的不断创新和市场的发展,亳州市将继续成为安徽省重要的经济中心和旅游目的地之一。
【本文由 “尼伽OLED透明拼接屏技术部门”原创,转载需备注来源和出处】
相关文章:

亳州市的自然风光与旅游资源:欣赏安徽省中部的壮丽景色
亳州市是中国安徽省的一个地级市,位于该省的中部。 亳州市辖区包括谯城区、涡阳县、蒙城县和利辛县等地。亳州市拥有悠久的历史和丰富的文化遗产,同时也以其独特的自然风光而闻名。 首先,让我们来了解一下亳州的历史和景点。亳州的历史可以…...
windows安装nvm以及解决yarn问题
源代码 下载 下一步一下步安装即可 检查是否安装成功 nvm出现上面的代码即可安装成功 常用命令 查看目前安装的node版本 nvm list [available]说明没有安装任何版本,下面进行安装 nvm install 18.14使用该版本 node use 18.14.2打开一个新的cmd输入node -…...
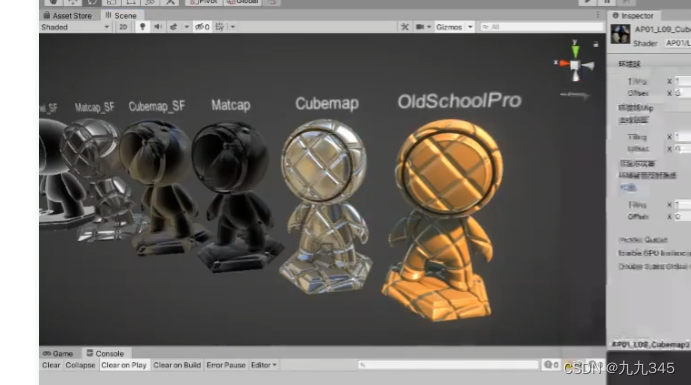
【TA 挖坑04】薄膜干涉 镭射材质 matcap
镭射材质,相对物理的实现? 万物皆可镭射,个性吸睛的材质渲染技术 - 知乎 (zhihu.com) 薄膜干涉材质,matcap更trick的方法?matcapremap, MatCap原理介绍及应用 - 知乎 (zhihu.com) 庄懂的某节课也做了mat…...

OpenCV13-图像噪声:椒盐噪声和高斯噪声
OpenCV13-图像噪声:椒盐噪声和高斯噪声 1.噪声种类2.椒盐噪声3.高斯噪声 1.噪声种类 图像噪声是指图像中的随机或非随机的不希望的视觉扰动。它可以出现在数字图像中的各种形式,例如颗粒状噪声、条纹、斑点、模糊、失真等。图像噪声可能是由于图像采集过…...

天堂2服务器基本设置
[system] server_nameLocal Server ——〉服务器名称 server_rulesPvP http_host127.0.0.1 ——〉HTTP注册页面(需先搭建IIS服务器) http_port8080 rs_host127.0.0.1——〉填你IP rs_port3724 ws_host127.0.0.1 ——〉填你的IP就对啦 ws_port8085 wor…...

如何解决网站被攻击的问题
在当今数字化时代,网站攻击已经成为互联网上的一个常见问题。这些攻击可能会导致数据泄漏、服务中断和用户信息安全问题。然而,我们可以采取一些简单的措施来解决这些问题,以确保网站的安全性和可用性。 使用强密码和多因素认证 密码是保护网…...

python爬虫入门详细教程-采集云南招聘网数据保存为csv文件
python爬虫之User-Agent大全、随机获取User-Agent 网站地址数据提取技术介绍采集目标流程分析python代码实现 网站地址 https://www.ynzp.com/ 这个网址特别适合新手拿来练习,你采集多了还有个验证码页面,验证码是4位数字,很清晰,…...

1.13.C++项目:仿muduo库实现并发服务器之TcpServer模块的设计
文章目录 一、LoopThreadPool模块二、实现思想(一)管理(二)流程(三)功能设计 三、代码 一、LoopThreadPool模块 TcpServer模块: 对所有模块的整合,通过 tcpserver 模块实例化的对象&…...
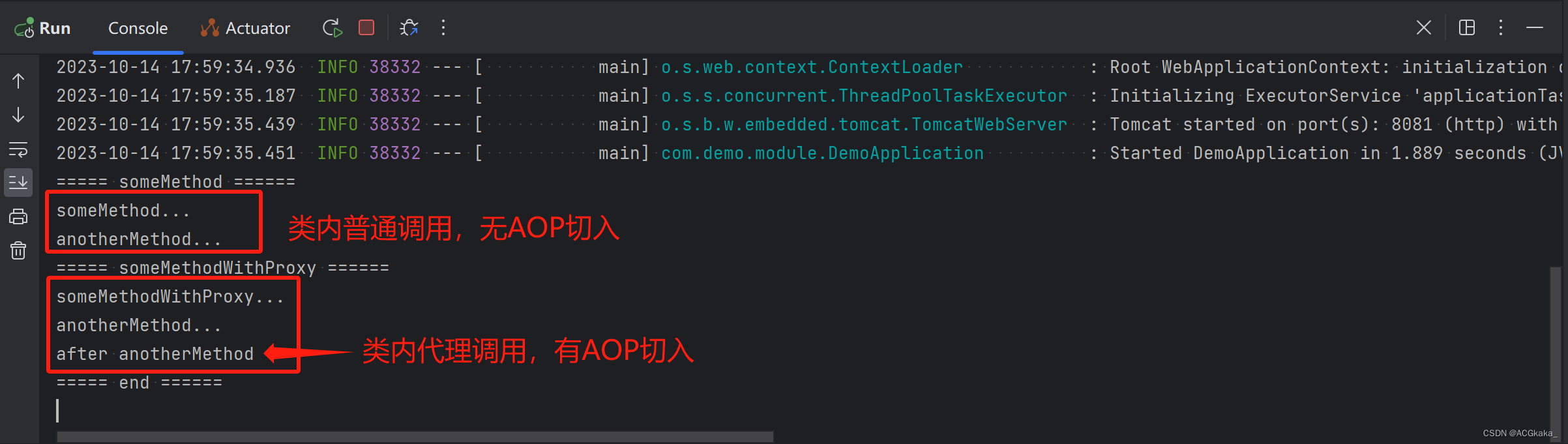
Spring(17) AopContext.currentProxy() 类内方法调用切入
目录 一、简介二、代码示例2.1 接口类2.2 接口实现类2.3 AOP切面类2.4 启动类(测试)2.5 执行结果 一、简介 背景: 在之前 Spring 的 AOP 用法中,只有代理的类才会被切入。例如:我们在 Controller 层调用 Service 的方式…...
)
自己的类支持基于范围的for循环 (深入探索)
自己的类支持基于范围的for循环 (深入探索) 编译器实际运行伪代码为: auto && __range range_expression; auto __begin begin_expr; auto __end end_expr; for (; __begin ! __end; __begin) {range_declaration *__begin;loop_statement }观察伪代码࿰…...
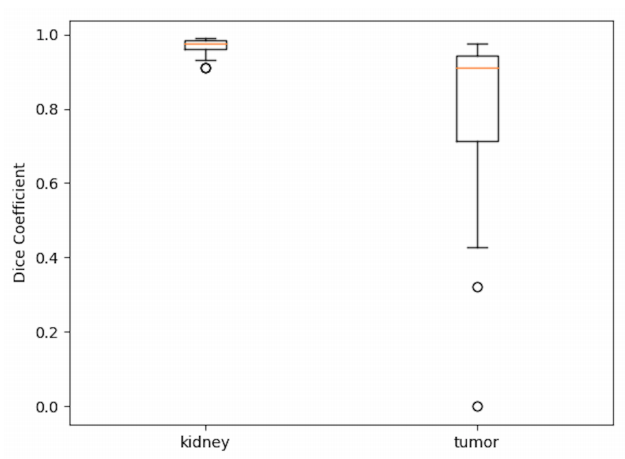
Multi Scale Supervised 3D U-Net for Kidney and Tumor Segmentation
目录 摘要1 引言2 方法2.1 预处理和数据增强2.2 网络的体系结构2.3 训练过程2.4 推理与后处理 3 实验与结果4 结论与讨论 摘要 U-Net在各种医学图像分割挑战中取得了巨大成功。一些新的、带有花里胡哨功能的架构可能在某些数据集中在使用最佳超参数时取得成功,但它们…...

《操作系统真象还原》第一章 部署工作环境
ref:https://www.bilibili.com/video/BV1kg4y1V7TV/?spm_id_from333.999.0.0&vd_source3f7ae4b9d3a2d84bf24ff25f3294d107 https://www.bilibili.com/video/BV1SQ4y1A7ZE/?spm_id_from333.337.search-card.all.click&vd_source3f7ae4b9d3a2d84bf24ff25f32…...
SpringCloud-Config
一、介绍 (1)服务注册中心 (2)管理各个服务上的application.yml,支持动态修改,但不会影响客户端配置 (3)一般将application.yml文件放在git上,客户端通过http/https方式…...

劣币驱良币的 pacing 之殇
都说 pacing 好 burst 孬(参见:为啥 pacing),就像都知道金币好,掺铁金币孬一样。可现实中掺铁的金币流通性却更好,劣币驱良币。劣币流通性好在卖方希望收到别人的良币而储存,而自己作为买方只使用劣币。 burst 和 pac…...
)
Gin 中的 Session(会话控制)
Session 介绍 session和cookie实现的底层目标是一致的,但是从根本而言实现的方法是不同的; session 是另一种记录客户状态的机制, 不同的是 Cookie 保存在客户端浏览器中,而 session保存 在服务器上 ; Session 的工作流程 当客户端浏览器第一次访问服务器并发送请求时,服…...
ChatGPT AIGC 实现数据分析可视化三维空间展示效果
使用三维空间图展示数据有以下一些好处: 1可视化复杂性:三维图可以展示三个或更多的变量,一眼就能看出数据各维度之间的关系,使复杂数据的理解和分析变得更为直观。 2检测模式和趋势:通过三维图,用户可以…...
Stable Diffusion 动画animatediff-cli-prompt-travel
基于 sd-webui-animatediff 生成动画或者动态图的基础功能,animatediff-cli-prompt-travel突破了部分限制,能让视频生成的时间更长,并且能加入controlnet和提示词信息控制每个片段,并不像之前 sd-webui-animatediff 的一套关键词控制全部画面。 动图太大传不上来,凑合看每…...

fatal error C1083: 无法打开包括文件: “ta_libc.h”: No such file or directory
用python做交易数据分析时,可以用talib库计算各类指标,这个库通过以下命令安装: pip install TA-Lib -i https://pypi.tuna.tsinghua.edu.cn/simple windows安装时可能出现本文标题所示的错误,可按如下步骤解决: 1、去…...

c 语言基础题目:L1-034 点赞
微博上有个“点赞”功能,你可以为你喜欢的博文点个赞表示支持。每篇博文都有一些刻画其特性的标签,而你点赞的博文的类型,也间接刻画了你的特性。本题就要求你写个程序,通过统计一个人点赞的纪录,分析这个人的特性。 …...
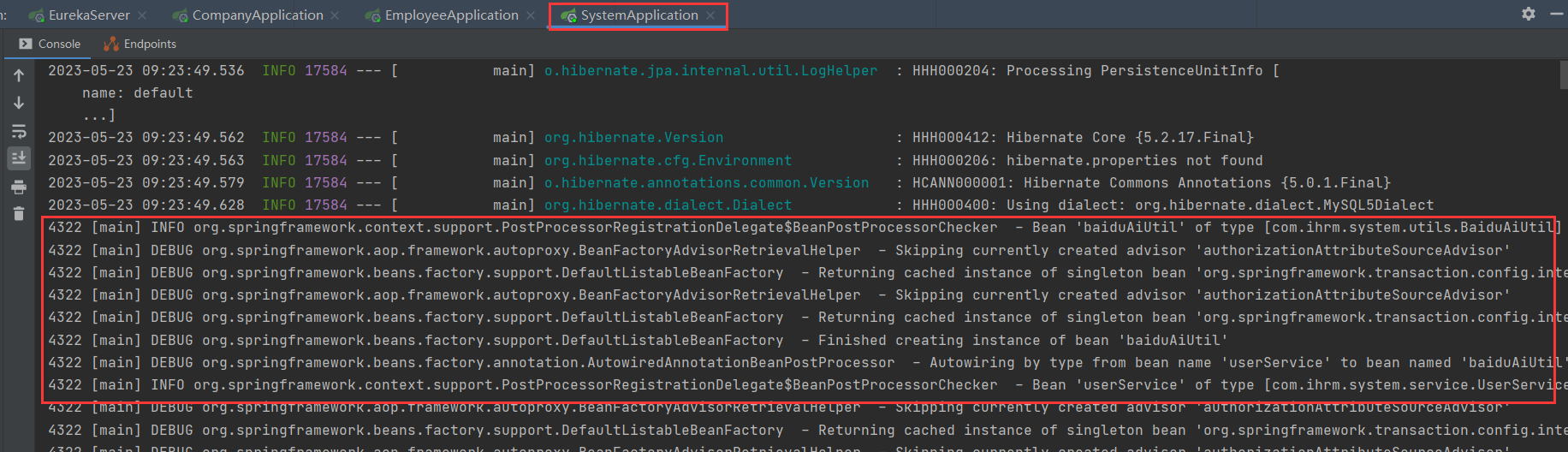
SaaS人力资源管理系统的Bug
SaaS人力资源管理系统的Bug Bug1【18】 这里我是直接把代码复制过来的,然后就有一个空白 这是因为它的代码有问题,原本的代码如下所示 <el-table-column fixed type"index" label"序号" width"50"></el-table…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
