[补题记录] Atcoder Beginner Contest 295(E)
URL:https://atcoder.jp/contests/abc295

目录
E
Problem/题意
Thought/思路
Code/代码
E
Problem/题意
给定长度为 N 的数组 A。进行如下操作:
- 若 Ai = 0,将 Ai 等概率地变为 1 ~ M 中的任意一个数;
- 对 A 排序;
问第 K 个数地期望是多少。
Thought/思路
概率 DP。(一开始想不明白这个公式,概率论白雪了)
设我们要求的 A[k] = x 且 P[i] 为 x = i 的概率,那么就有如下公式:
关于这条公式地推导:https://zhuanlan.zhihu.com/p/617048570

因此接下来的问题就变成了:对于每个 i,求出 P(A[k] >= i)。
但是我们不知道 A[k] 该怎么取值,所以还需要将 P(A[k] >= i) 转换为:后面 N - K + 1 个数 >= i 的概率,也就是 [K, N] 中的数都 >= i 的概率。(假设已经排好序)
显然 [K, N] 中的数不会都 >= i,而一般的情况就是:[K, N] 中的前一部分的数 < i、后一部分的数 >= i。
对于前一部分,我们需要依靠 0 来变成 >= i 的数去替换他们,所以记录前一部分的数的个数为 need,这代表了所需要的 0 的最少数量。
也就是说,如果 0 的数量(设为 zero)zero < need,那么就永远不可能满足 [K, N] 中的数都 >= i,概率为 0;反之,如果 need <= 0,就一定满足 [K, N] 中的数都 >= i,概率为 1;
基于概率为 0 的那种情况,就一定能保证 need <= zero。
而 need 是需要的 0 的最少数量,那么我们就可以设:有 need 个 0 变成了 >= i 的数,其带来的概率为:
其中 P = (m - i + 1) / m,意思是:取出 >= i 的数的概率。
显然一共有 zero 个 0 可以使用,所以考虑 [need, zero] 每一种情况即可。
Code/代码
#include "bits/stdc++.h"#define int long longconst int mod = 998244353;int n, m, k, a[2007], fact[2007], invf[2007];int ksm(int a, int b) {int res = 1;while (b > 0) {if (b & 1) res = res * a % mod;a = a * a % mod;b /= 2;}return res;
}void init() {fact[0] = 1, invf[0] = ksm(1, mod - 2);for (int i = 1; i <= 2000; ++ i) {fact[i] = fact[i - 1] * i % mod;invf[i] = ksm(fact[i], mod - 2) % mod;}
}int C(int x, int y) {if (x < y) return 0;return fact[x] * invf[y] % mod * invf[x - y] % mod;
}signed main() {std::cin >> n >> m >> k;for (int i = 1; i <= n; ++ i) std::cin >> a[i];init();int ans = 0;for (int i = 1; i <= m; ++ i) {int zero = 0, need = n - k + 1;for (int j = 1; j <= n; ++ j) {if (a[j] >= i) need --;if (a[j] == 0) zero ++;}if (need <= 0 or need > zero) { // [k, n] 都 >= i,概率为 1;[k, n] 小于 i 的个数,0 补不上,概率为 0。ans = (ans + (need <= 0 ? 1 : 0)) % mod;continue;}int p1 = (m - i + 1) * ksm(m, mod - 2) % mod; // 选出的数 >= i 的概率 p:(m - i + 1) / mint p2 = (i - 1) * ksm(m, mod - 2) % mod; // 1 - p:(i - 1) / mstd::vector <int> dp1(zero + 1), dp2(zero + 1);dp1[0] = dp2[0] = ksm(1, mod - 2);for (int j = 1; j <= zero; ++ j) {dp1[j] = dp1[j - 1] * p1 % mod;dp2[j] = dp2[j - 1] * p2 % mod;}// 用 0 补充 >= i 的数for (int j = need; j <= zero; ++ j) {ans = (ans + C(zero, j) * dp1[j] % mod * dp2[zero - j] % mod) % mod;}}std::cout << ans;return 0;
}相关文章:
[补题记录] Atcoder Beginner Contest 295(E)
URL:https://atcoder.jp/contests/abc295 目录 E Problem/题意 Thought/思路 Code/代码 E Problem/题意 给定长度为 N 的数组 A。进行如下操作: 若 Ai 0,将 Ai 等概率地变为 1 ~ M 中的任意一个数;对 A 排序; …...
解决git在window11操作很慢,占用很大cpu的问题
【git在window11操作很慢,占用很大cpu,最后也执行失败】 在谷歌输入:git very slow in window 11。通过下面链接终于找到了解决方案: https://www.reddit.com/r/vscode/comments/sulebx/slow_git_in_wsl_after_updating_to_window…...
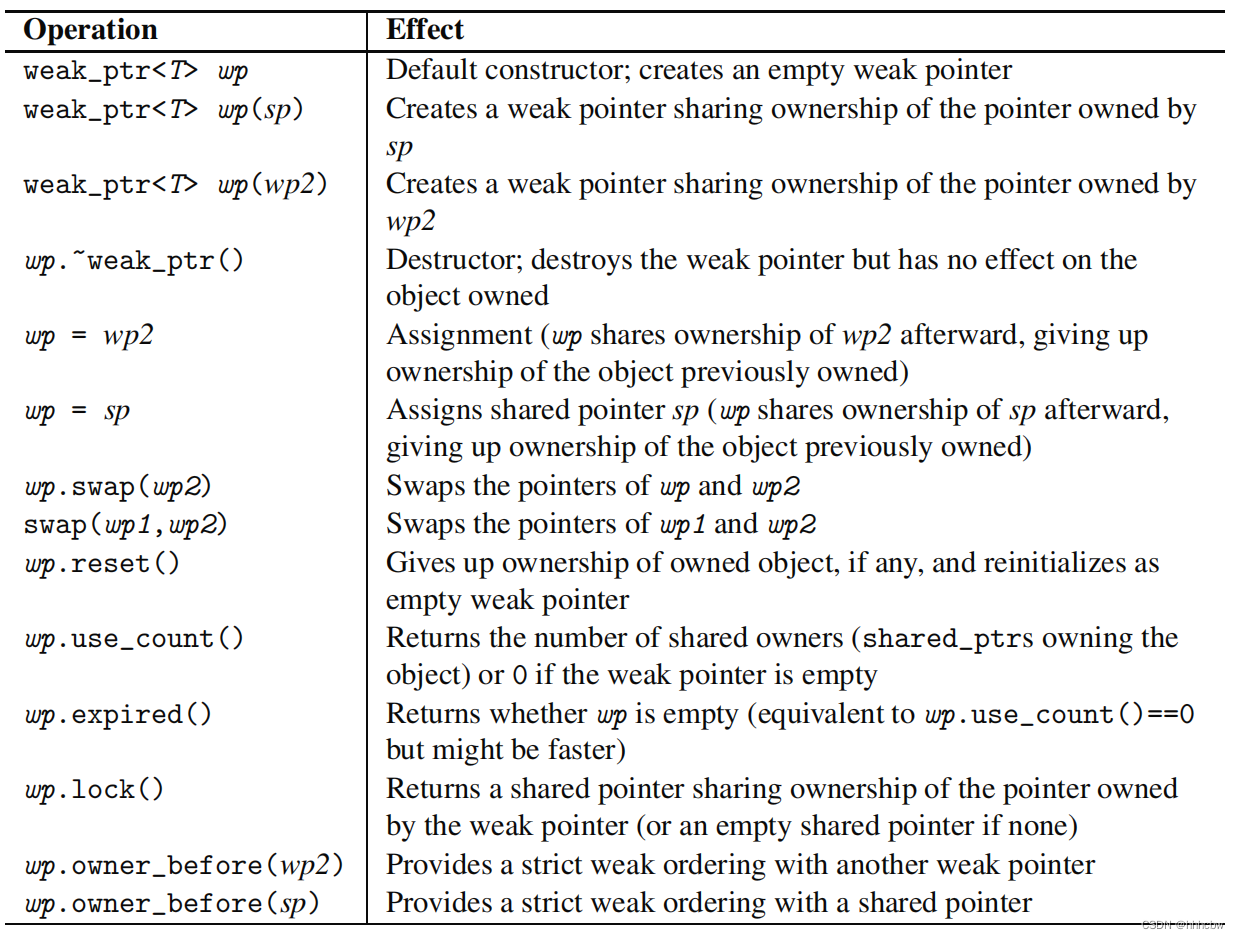
C++智能指针(二)——weak_ptr初探
文章目录 1. shared_ptr 存在的问题2. 使用weak_ptr2.1 初始化 weak_ptr2.2 访问数据 3. 附录4. 参考文献 1. shared_ptr 存在的问题 与 shared_ptr 的引入要解决普通指针存在的一些问题一样,weak_ptr 的引入,也是因为 shared_ptr 本身在某些情况下&…...
)
540 - Team Queue (UVA)
题目链接如下: Online Judge 对比刘汝佳的代码,我没有用queue来排整个队伍,因为那样的话遍历整个队伍太麻烦,vector比较方便。但vector删除元素比较耗时,所以就不删了,仅仅用pivot来指代目前队伍的开始。…...
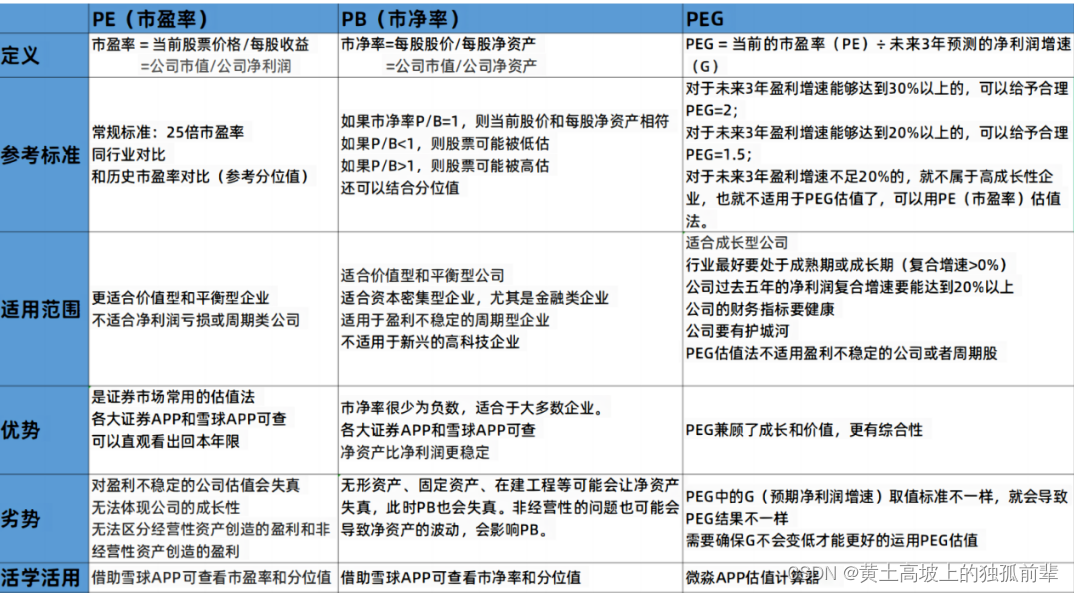
投资组合之如何估值
文章目录 如何估值一、PE估值法1、PE估值法的定义2、参考标准(1)常规标准:25倍合理市盈率。(2)同行业对比。(3)跟历史市盈率相比。 3、PE估值法的适用范围4、PE估值法的优势5、PE估值法的劣势&a…...
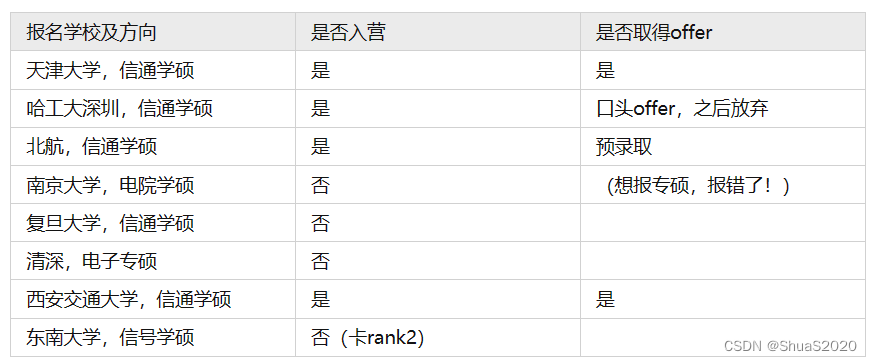
2024届通信工程保研经验分享(预推免入营即offer)
2024届通信工程保研经验分享(预推免入营即offer) BackGround夏令营情况:预推免情况: BackGround 本科院校:末九 专业:通信工程 rank:3/123(预推免绩点排名)࿰…...

L2-025 分而治之 - java
L2-025 分而治之 时间限制 600 ms 内存限制 64 MB 题目描述: 分而治之,各个击破是兵家常用的策略之一。在战争中,我们希望首先攻下敌方的部分城市,使其剩余的城市变成孤立无援,然后再分头各个击破。为此参谋部提供了若…...
Python+高光谱数据预处理-机器学习-深度学习-图像分类-参数回归
涵盖高光谱遥感数据处理的基础、python开发基础、机器学习和应用实践。重点解释高光谱数据处理所涉及的基本概念和理论,旨在帮助学员深入理解科学原理。结合Python编程工具,专注于解决高光谱数据读取、数据预处理、高光谱数据机器学习等技术难题…...

免费 AI 编程助手 Amazon CodeWhisperer 体验
文章作者:文章作者:米菲爸爸 2022 年 6 月 23 亚马逊云科技就已经推出了 Amazon CodeWhisperer(预览版)。经过不到一年的测试和 AIGC的飓风在 2023 年 4 月 18 日实时 AI 编程助手 Amazon CodeWhisperer正式可用 Amazon CodeWhis…...
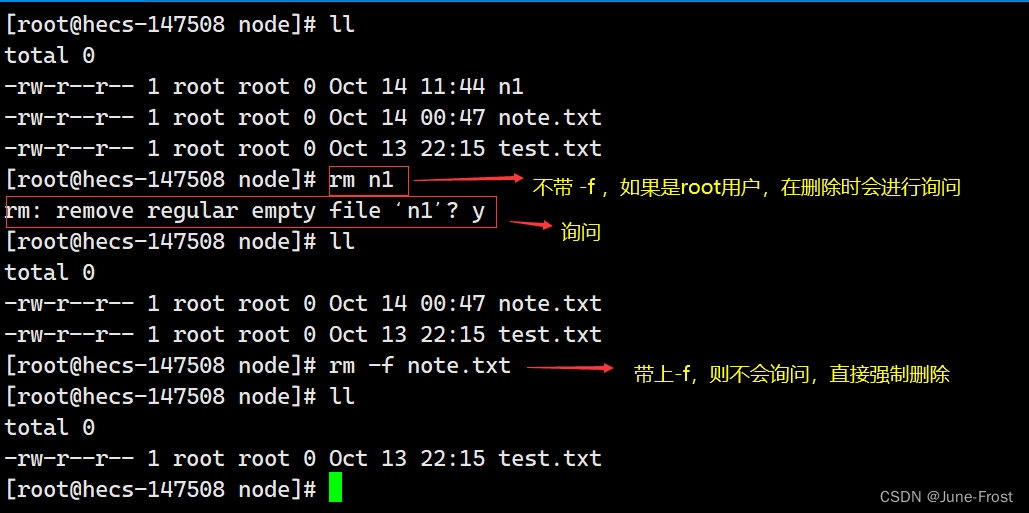
【Linux】从零开始学习Linux基本指令(一)
🚩纸上得来终觉浅, 绝知此事要躬行。 🌟主页:June-Frost 🚀专栏:Linux入门 🔥该文章主要了解Linux操作系统下的基本指令。 目录: ⌛️指令的理解⏳目录和文件的理解⏳一些常见指令✉…...

Java GC 算法
一、概述 理解Java虚拟机垃圾回收机制的底层原理,是成为一个高级Java开发者的基本功。本文从底层的垃圾回收算法开始,着重去阐释不同垃圾回收器在算法设计和实现时的一些技术细节,去探索「why」这一部分,通过对比不同的垃圾回收算…...

vue3 v-html中使用v-viewer
安装:npm install v-viewernext 在main.js中配置 import “viewerjs/dist/viewer.css”; import Viewer from “v-viewer”; app.use(Viewer, { Options: { inline: true, //默认值:false。启用内联模式。 button: true, //在查看器的右上角显示按钮。 …...
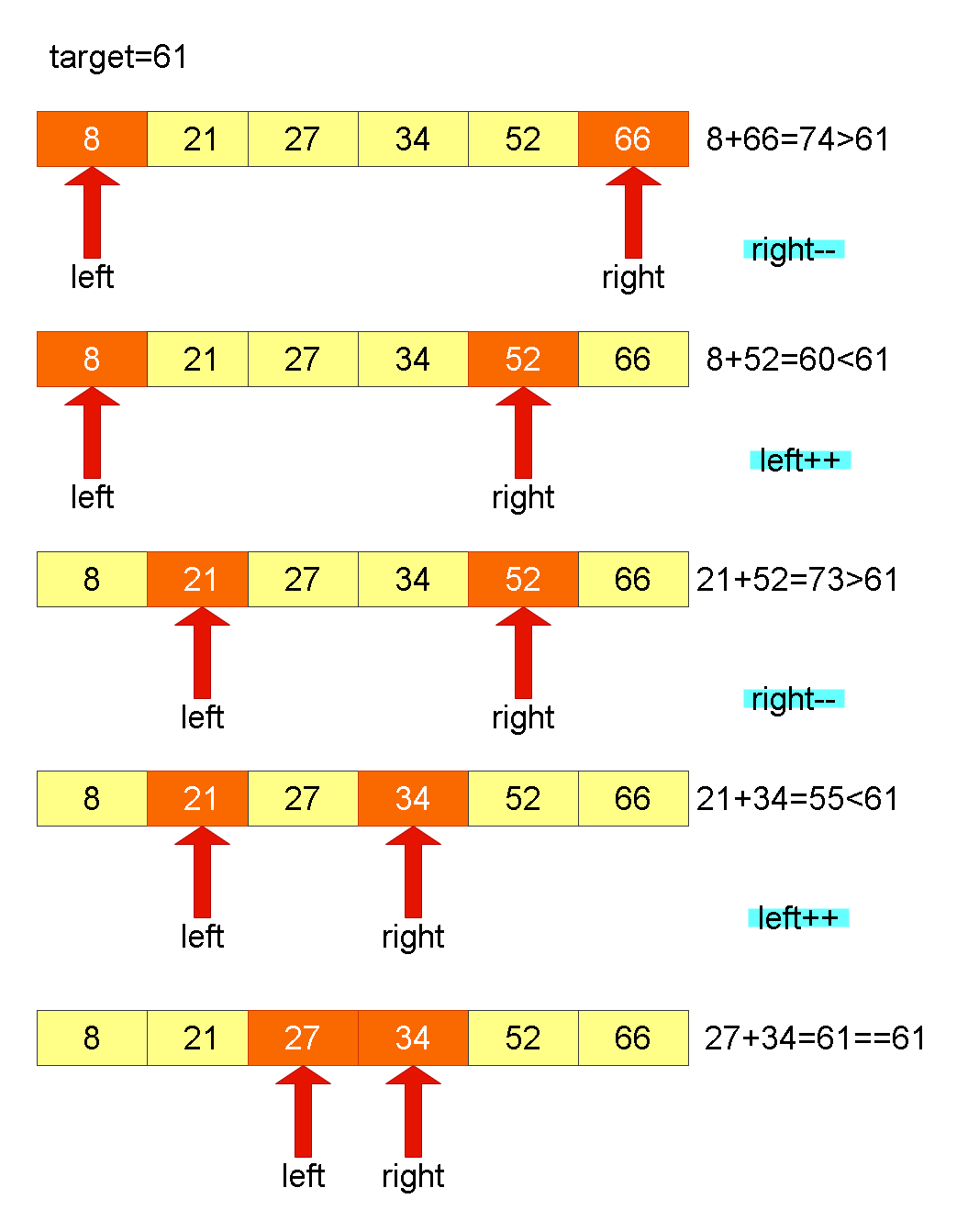
Leetcode算法解析——查找总价格为目标值的两个商品
1. 题目链接:LCR 179. 查找总价格为目标值的两个商品 2. 题目描述: 商品价格按照升序记录于数组 price。请在购物车中找到两个商品的价格总和刚好是 target。若存在多种情况,返回任一结果即可。 示例 1: 输入:price …...

unity游戏开发引擎unity3D开发
Unity(也被称为Unity3D)是一款强大的跨平台游戏引擎,用于开发2D和3D游戏,以及其他交互式应用程序。以下是Unity游戏开发的一般步骤: 安装和设置Unity: 首先,您需要下载并安装Unity。确保选择适…...

iptables
目录 iptables 匹配规则:由上到下依次匹配,一旦匹配不再匹配 参数 知识点 REJECT与DROP REJECT与DROP的区别 当使用的时REJECT时,客户端访问迅速返回的值是拒绝连接 当使用的是DROP时,返回的时连接超时 REJECT与drop适用…...
竞赛 深度学习LSTM新冠数据预测
文章目录 0 前言1 课题简介2 预测算法2.1 Logistic回归模型2.2 基于动力学SEIR模型改进的SEITR模型2.3 LSTM神经网络模型 3 预测效果3.1 Logistic回归模型3.2 SEITR模型3.3 LSTM神经网络模型 4 结论5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 …...

Spark入门
目录 Spark入门: 概述历史概述SparkCore:RDDSparkSQL:SparkStreamingSpark内核调优 Spark概述 回顾: Hadoop HDFS存储 MR分析计算 YARN调度 Hadoop的MR计算中的shuffle需要落盘,速度不够快。 Spark是一种基于内存的分析计算引擎。 历史…...
react–antd 实现TreeSelect树形选择组件,实现点开一层调一次接口
效果图: 注意: 当选择“否”,开始调接口,不要把点击调接口写在TreeSelect组件上,这样会导致问题出现,没有层级了 部分代码:...

android 固定进度环形刷新效果
android 固定进度无限旋转的环形效果 效果图 效果视频: Record_2023-10-13-17-17-19[1] Activity 中使用 val rotation: ObjectAnimator ObjectAnimator.ofFloat(progressBar, "rotation", 0f, 360f) rotation.duration 000 // 旋转持续时间为2秒 rot…...

python jieba 词性标注 中文词性分类 nlp jieba.posseg
参考:https://blog.csdn.net/yellow_python/article/details/83991967 from jieba.posseg import dt dt.word_tag_tab[好看] >>> vflag_en2cn { ‘a’: ‘形容词’, ‘ad’: ‘副形词’, ‘ag’: ‘形语素’, ‘an’: ‘名形词’, ‘b’: ‘区别词’, ‘…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
