【考研数学】线性代数第六章 —— 二次型(2,基本定理及二次型标准化方法)
文章目录
- 引言
- 一、二次型的基本概念及其标准型
- 1.2 基本定理
- 1.3 二次型标准化方法
- 1. 配方法
- 2. 正交变换法
- 写在最后
引言
了解了关于二次型的基本概念以及梳理了矩阵三大关系后,我们继续往后学习二次型的内容。
一、二次型的基本概念及其标准型
1.2 基本定理
定理 1 —— (标准型定理)任何二次型 X T A X \pmb{X}^T\pmb{AX} XTAX 总可以经过可逆的线性变换 X = P Y \pmb{X=PY} X=PY ,即 P \pmb{P} P 为可逆矩阵,把二次型 f ( X ) f(\pmb{X}) f(X) 化为标准型,即 f ( X ) = Y T ( P T A P ) Y = l 1 y 1 2 + l 2 y 2 2 + ⋯ + l m y m 2 , f(\pmb{X})=\pmb{Y}^T(\pmb{P}^T\pmb{AP})\pmb{Y}=l_1y_1^2+l_2y_2^2+\cdots+l_my_m^2, f(X)=YT(PTAP)Y=l1y12+l2y22+⋯+lmym2, 其中 m m m 为标准型中非零系数的个数。
定理 2 —— (惯性定理)二次型的标准型的系数中,正、负系数的个数保持不变,分别称为二次型的正、负惯性指数。
定理 3 —— (矩阵合同定理)设 A , B \pmb{A,B} A,B 为 n n n 阶实对称矩阵,则 A ≃ B \pmb{A\simeq B} A≃B 的充分必要条件是 A , B \pmb{A,B} A,B 的特征值中正、负及零的个数相同。
从这个角度也可以理解昨天那篇文章中,为什么实对称矩阵相似一定合同。因为相似的话特征值都一样了,自然正、负及零的个数相同;反之,合同的话,只是个数相同,不能推出特征值相同。
定理 4 —— 对二次型 f ( x 1 , x 2 , ⋯ , x n ) = X T A X ( A T = A ) f(x_1,x_2,\cdots,x_n)=\pmb{X^TAX(A^T=A)} f(x1,x2,⋯,xn)=XTAX(AT=A) ,一定存在正交矩阵 Q \pmb{Q} Q ,使得经可逆线性变换 X = Q Y \pmb{X=QY} X=QY 后,有 X T A X = Y T ( Q T A Q ) Y = λ 1 y 1 2 + λ 2 y 2 2 + ⋯ + λ n y n 2 , \pmb{X^TAX=Y^T(Q^TAQ)Y}=\lambda_1y_1^2+\lambda_2y_2^2+\cdots+\lambda_ny_n^2, XTAX=YT(QTAQ)Y=λ1y12+λ2y22+⋯+λnyn2, 其中, λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn 为矩阵 A \pmb{A} A 的特征值。
1.3 二次型标准化方法
1. 配方法
即通过配方的方法,把二次型化为若干部分的平方和与差,然后进行变换的方法。
如:设 f ( x 1 , x 2 , x 3 ) = x 1 2 + 2 x 2 2 − 5 x 3 2 − 2 x 1 x 2 + 2 x 2 x 3 = X T A X f(x_1,x_2,x_3)=x_1^2+2x_2^2-5x_3^2-2x_1x_2+2x_2x_3=\pmb{X^TAX} f(x1,x2,x3)=x12+2x22−5x32−2x1x2+2x2x3=XTAX ,其中 A = [ 1 − 1 0 − 1 2 1 0 1 − 5 ] , X = [ x 1 x 2 x 3 ] \pmb{A}=\begin{bmatrix} 1 & -1 & 0\\ -1 & 2 & 1\\ 0 & 1 & -5 \end{bmatrix},\pmb{X}=\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} A= 1−10−12101−5 ,X= x1x2x3 ,配方得 f ( x 1 , x 2 , x 3 ) = x 1 2 + 2 x 2 2 − 5 x 3 2 − 2 x 1 x 2 + 2 x 2 x 3 = ( x 1 − x 2 ) 2 + ( x 2 − x 3 ) 2 − 6 x 3 2 , f(x_1,x_2,x_3)=x_1^2+2x_2^2-5x_3^2-2x_1x_2+2x_2x_3=(x_1-x_2)^2+(x_2-x_3)^2-6x_3^2, f(x1,x2,x3)=x12+2x22−5x32−2x1x2+2x2x3=(x1−x2)2+(x2−x3)2−6x32, 令 x 1 − x 2 = y 1 , x 2 − x 3 = y 2 , x 3 = y 3 x_1-x_2=y_1,x_2-x_3=y_2,x_3=y_3 x1−x2=y1,x2−x3=y2,x3=y3 ,即有 x 1 = y 1 + y 2 − y 3 , x 2 = y 2 − y 3 , x 3 = y 3 x_1=y_1+y_2-y_3,x_2=y_2-y_3,x_3=y_3 x1=y1+y2−y3,x2=y2−y3,x3=y3 ,用矩阵形式表达,即 X = P Y \pmb{X=PY} X=PY ,其中 P = [ 1 1 − 1 0 1 − 1 0 0 1 ] , Y = [ y 1 y 2 y 3 ] \pmb{P}=\begin{bmatrix} 1 & 1 & -1\\ 0 & 1 & -1\\ 0 & 0 & 1 \end{bmatrix},\pmb{Y}=\begin{bmatrix} y_1 \\ y_2 \\ y_3 \end{bmatrix} P= 100110−1−11 ,Y= y1y2y3 。作可逆线性变换 X = P Y \pmb{X=PY} X=PY ,使得 f ( x 1 , x 2 , x 3 ) = y 1 2 + y 2 2 − 6 y 3 2 . f(x_1,x_2,x_3)=y_1^2+y_2^2-6y_3^2. f(x1,x2,x3)=y12+y22−6y32.
2. 正交变换法
即利用定理 4 ,把二次型标准化。其基本步骤如下:
(1)由特征方程 ∣ λ E − A ∣ = 0 |\lambda \pmb{E-A}|=0 ∣λE−A∣=0 ,求出矩阵 A \pmb{A} A 的特征值 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn ;
(2)求出方程组 ( λ i E − A ) X = 0 ( i = 1 , 2 , ⋯ , n ) (\lambda_i\pmb{E-A})\pmb{X}=\pmb{0}(i=1,2,\cdots,n) (λiE−A)X=0(i=1,2,⋯,n)(重特征值只代一次)的基础解系,从而获得矩阵 A \pmb{A} A 的线性无关的特征向量 ξ 1 , ξ 2 , ⋯ , ξ n \pmb{\xi_1,\xi_2,\cdots,\xi_n} ξ1,ξ2,⋯,ξn ;
(3)将 ξ 1 , ξ 2 , ⋯ , ξ n \pmb{\xi_1,\xi_2,\cdots,\xi_n} ξ1,ξ2,⋯,ξn 进行施密特正交化(只在重特征值对应的线性无关的特征向量内部进行)和规范化,得到矩阵 A \pmb{A} A 的两两正交规范的特征向量 γ 1 , γ 2 , ⋯ , γ n \pmb{\gamma_1,\gamma_2,\cdots,\gamma_n} γ1,γ2,⋯,γn ;
(4)令 Q = ( γ 1 , γ 2 , ⋯ , γ n ) \pmb{Q}=(\pmb{\gamma_1,\gamma_2,\cdots,\gamma_n}) Q=(γ1,γ2,⋯,γn) ,则 Q \pmb{Q} Q 为正交矩阵,且 Q T A Q = [ λ 1 ⋱ λ n ] \pmb{Q^TAQ}=\begin{bmatrix} \lambda_1 & & \\ & \ddots & \\ & & \lambda_n \end{bmatrix} QTAQ= λ1⋱λn ;
(5)作正交变换 X = Q Y \pmb{X=QY} X=QY ,则 f ( x 1 , x 2 , ⋯ , x n ) = X T A X ⟹ Y T ( Q T A Q ) Y = λ 1 y 1 2 + λ 2 y 2 2 + ⋯ + λ n y n 2 f(x_1,x_2,\cdots,x_n)=\pmb{X^TAX\Longrightarrow Y^T(Q^TAQ)Y}=\lambda_1y_1^2+\lambda_2y_2^2+\cdots+\lambda_ny_n^2 f(x1,x2,⋯,xn)=XTAX⟹YT(QTAQ)Y=λ1y12+λ2y22+⋯+λnyn2
1,采用正交变换法化标准型时,标准型的系数一定为矩阵 A \pmb{A} A 的特征值。配方法则不一定,但是系数中正、负系数的个数是唯一的。
2,二次型的规范型是唯一的。
3,正交变换不改变向量的长度,即 Q \pmb{Q} Q 为正交矩阵,且向量 X , Y \pmb{X,Y} X,Y 满足 X = Q Y \pmb{X=QY} X=QY ,则有 ∣ X ∣ = ∣ Y ∣ |\pmb{X}|=|\pmb{Y}| ∣X∣=∣Y∣ 。因为 ∣ X ∣ 2 = X T X = ( Q Y ) T Q Y = Y T ( Q Q ) Y = Y T Y = ∣ Y ∣ 2 |\pmb{X}|^2=\pmb{X}^T\pmb{X}=(\pmb{QY})^T\pmb{QY}=\pmb{Y}^T(\pmb{Q}\pmb{Q)\pmb{Y}}=\pmb{Y}^T\pmb{Y}=|\pmb{Y}|^2 ∣X∣2=XTX=(QY)TQY=YT(QQ)Y=YTY=∣Y∣2 , ∣ X ∣ , ∣ Y ∣ > 0 \pmb{|X|,|Y|}>0 ∣X∣,∣Y∣>0 ,故 ∣ X ∣ = ∣ Y ∣ |\pmb{X}|=|\pmb{Y}| ∣X∣=∣Y∣ 。
写在最后
先到这吧,慢慢来,做点题目巩固下。下一篇文章我们来学习关于正定矩阵的内容。
相关文章:
)
【考研数学】线性代数第六章 —— 二次型(2,基本定理及二次型标准化方法)
文章目录 引言一、二次型的基本概念及其标准型1.2 基本定理1.3 二次型标准化方法1. 配方法2. 正交变换法 写在最后 引言 了解了关于二次型的基本概念以及梳理了矩阵三大关系后,我们继续往后学习二次型的内容。 一、二次型的基本概念及其标准型 1.2 基本定理 定理…...
Raven2靶机渗透
1. 信息收集 1.1 主机探测 sudo arp-scan -l1.2 端口扫描 nmap -p- -A 192.168.16.185开放了80端口,尝试登录网址查看信息,通过浏览器插件找出指纹 1.3 目录扫描 访问登录界面,发现remember Me怀疑是shiro界面 登录/vendor/界面࿰…...

UE5中双pass解决半透明材质乱序问题
透明度材质乱序问题一直是半透明效果时遇到的比较多的问题,用多pass方案只能说一定程度上解决,当遇到多半透明物体穿插等情况时,仍然不能完美解决。 双pass方案Unity用的比较多,因为Unity支持多个pass绘制。在UE中我们可以以复制多…...
Cisdem Video Player for mac(高清视频播放器) v5.6.0中文版
Cisdem Video Player mac是一款功能强大的视频播放器,适用于 macOS 平台。它可用于播放不同格式的视频文件,并具有一些实用的特性和功能。 Cisdem Video Player mac 中文版软件特点 多格式支持:Cisdem Video Player 支持几乎所有常见的视频格…...

数据库管理-第109期 19c OCM考后感(20231015)
数据库管理-第109期 19c OCM考后感(202301015) 距离上一篇又过了两周多,为啥又卡了这么久,主要是后面几个问题:1. 9月1日的19c OCM upgrade考试木有过,因为有一次免费补考机会就又预约了10月8日的考试&…...
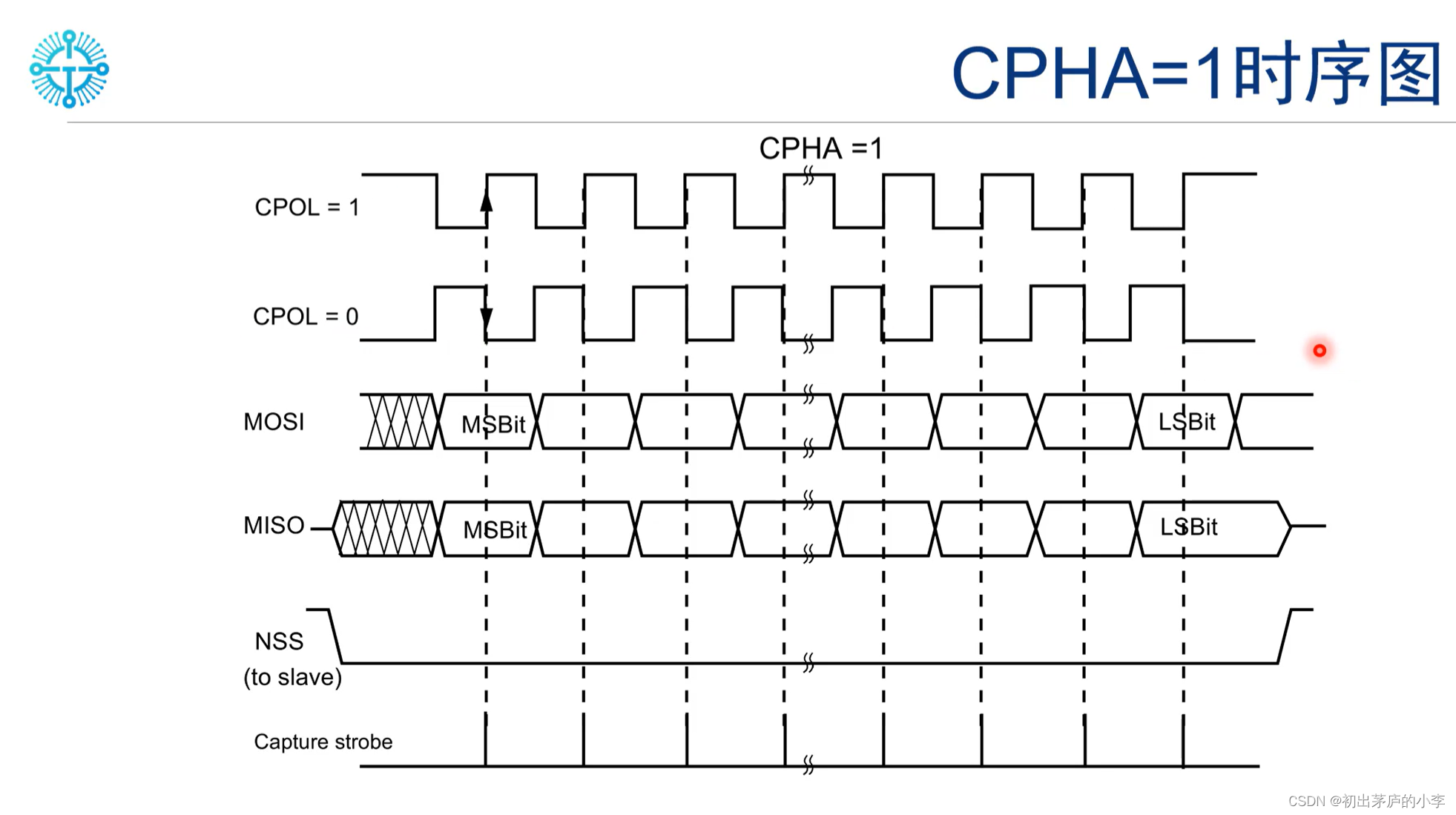
初出茅庐的小李博客之SPI工作模式
SPI的工作模式 SPI(Serial Peripheral Interface)是一种同步串行通信协议,常用于连接微控制器和外围设备。SPI有四种模式,分别是0、1、2、3模式。 0模式:时钟空闲时为低电平,数据在时钟的下降沿采样&#…...

SpringCloud-Bus
一、介绍 (1)bus搭配config可以实现客户端配置自动刷新 (2)bus支持两种消息代理,rabbitmq和kafka (3)使用topic模式分发消息 二、项目搭建(广播) (1&#…...
Adobe2024 全家桶更新了,PS、Ai、AE、PR应用尽有
Adobe2024 全家桶更新了,包含的PS、Ai、AE、PR......个人学习,专业领域都是必不可少的软件都有,需要的不要错过了。 如果你不知道从哪里安装这些工具,小编为大家带来了破J版资源,附上详细的安装包及安装教程。 Mac软件…...

【斗破年番】彩鳞换装美翻,雁落天惨死,萧炎暗杀慕兰三老遇险,彩鳞霸气护夫
Hello,小伙伴们,我是小郑继续为大家深度解析斗破苍穹年番资讯。 斗破苍穹动画已经更新了,小医仙与萧炎相认,三国联军撤退,随后彩鳞与萧炎以及小医仙夜晚相会,一起制定了刺杀行动。从官方公布的第68集预告,彩…...

华为端到端战略管理体系(DSTE开发战略到执行)的运作日历图/逻辑图及DSTE三大子流程介绍
华为端到端战略管理体系(DSTE开发战略到执行)的运作日历图/逻辑图及DSTE三大子流程介绍 本文作者 | 谢宁,《华为战略管理法:DSTE实战体系》、《智慧研发管理》作者 添加图片注释,不超过 140 字(可选&#…...
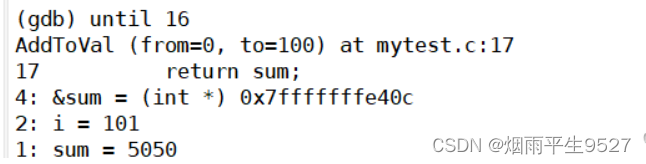
Linux友人帐之调试器--gdb的使用
一、debug和realease版本的区别 区别 debug是给程序员用的版本,添加了调试信息,用于解决软件或程序中出现的问题,realease是发行给客户使用的版本,并未添加调试信息,只需要给客户提供优越的产品使用环境即可ÿ…...
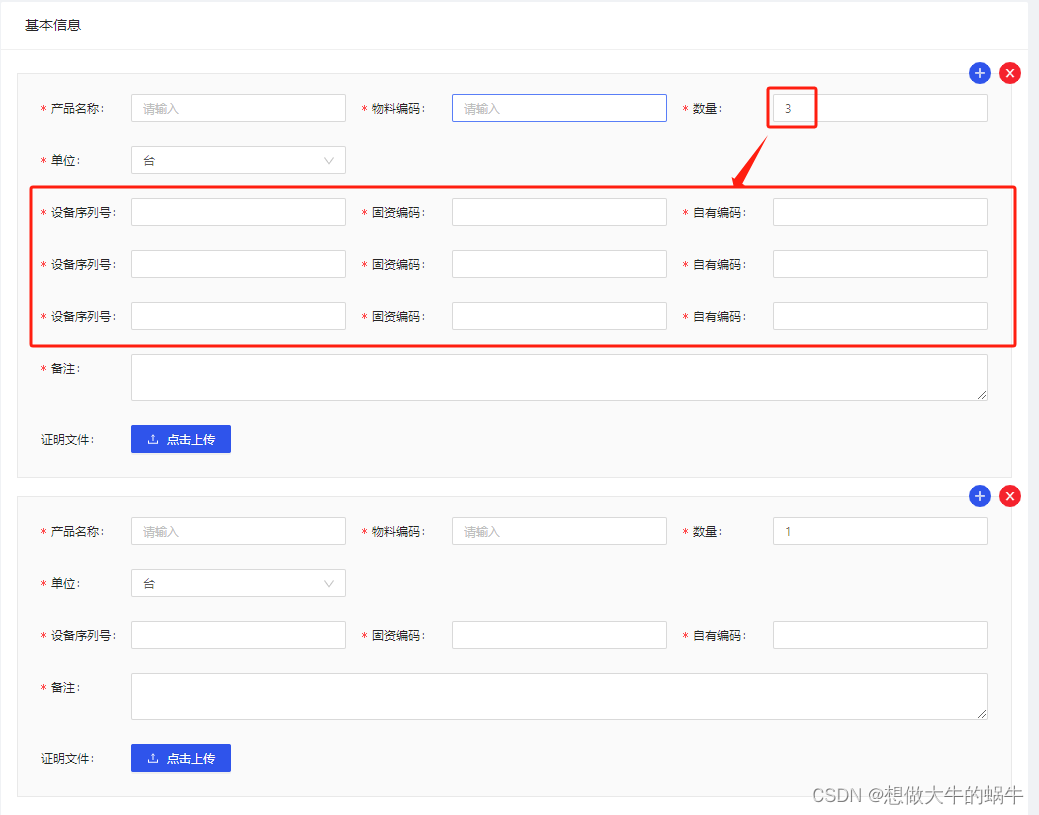
antd pro form 数组套数组 form数组动态赋值 shouldUpdate 使用
antd form中数组套数组 form数组动态变化 动态赋值 需求如上,同时添加多个产品,同时每个产品可以增加多台设备,根据设备增加相应编号,所以存在数组套数组,根据数组值动态变化 使用的知识点 form.list form中的数组…...

动态规划:918. 环形子数组的最大和
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》《算法》 文章目录 前言一、题目解析二、解题思路解题思路状态表示状态转移方程初始化填表顺序返回值 三、代码实现总结 前言 本篇文章仅是作为小白的我的一些理解,,…...

毅速丨模具3D打印材料有哪些选择
当前1.2709和CX是市面上最常用的3D打印模具钢材料,模具3D打印有没有更多的材料选择呢? 据了解,上海毅速推出的几款3D打印新材料正在被越来越多的行业所采用。如毅速的EM191S高性能高抛光不锈钢粉末,这款材料的抗开裂和耐腐蚀性能是…...
Springcloud笔记(1)-微服务和springcloud介绍
微服务简介 就是将一个大的应用,拆分成多个小的模块,每个模块都有自己的功能和职责,每个模块可以 进行交互,这就是微服务对于微服务,业界没有严格统一的定义,但是作为“微服务”这名词的发明人,…...
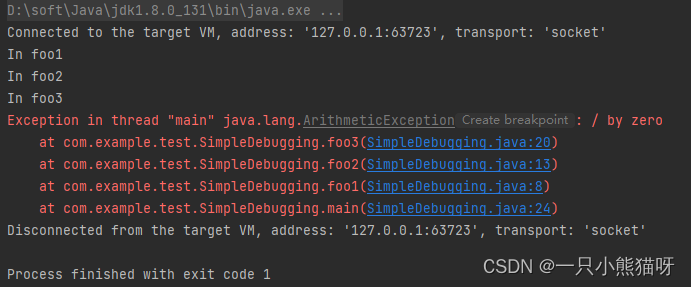
十六、代码校验(4)
本章概要 调试 使用 JDB 调试图形化调试器 调试 尽管聪明地使用 System.out 或日志信息能给我们带来对程序行为的有效见解,但对于困难问题来说,这种方式就显得笨拙且耗时了。 你也可能需要更加深入地理解程序,仅依靠打印日志做不到。此时…...

【已解决】No Python at ‘D:\Python\python.exe‘
起因,我把我的python解释器,重新移了个位置,导致我在Pycharm中的爬虫项目启动,结果出现这个问题。 然后,从网上查到了这篇博客: 【已解决】No Python at ‘D:\Python\python.exe‘-CSDN博客 但是,按照上述…...

蓝桥杯双周赛算法心得——数树数(dfs)
大家好,我是晴天学长,一个简单的dfs思想,需要的小伙伴可以关注支持一下哦!后续会继续更新的。 1) .数树数 2) .算法思路 代码的主要逻辑是: 1.使用Scanner读取输入的整数n和q,其中n表示测试用例的数量&am…...
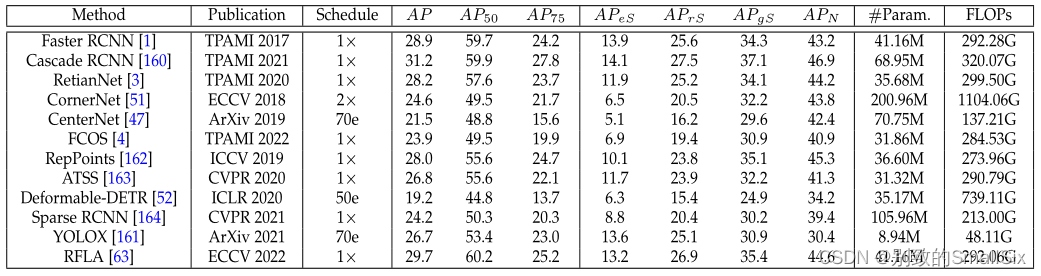
综述:大规模小目标检测
论文地址: Towards Large-Scale Small Object Detection: Survey and Benchmarksarxiv.org/abs/2207.14096 目录 摘要 1.Introduction 1.1 与之前综述的比较 1.2 总结 2.小目标检测回顾 2.1 问题定义 2.2 主要挑战 2.3 小目标检测算法回顾 3.小目标检测的数据集 …...

ORACLE XXX序列 goes below MINVALUE 无法实例化的处理办法
--序列增加区分 --删除未使用序列表 DECLARE V_CNT INT; BEGINSELECT COUNT(*) INTO V_CNT FROM USER_SEQUENCES WHERE SEQUENCE_NAME SEQ_INTELLECT_BIZ_DETAIL_ID;IF V_CNT1 THEN BEGINEXECUTE IMMEDIATE DROP SEQUENCE SEQ_INTELLECT_BIZ_DETAIL_ID;END;END IF; END; / ---…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...

【Axure高保真原型】图片列表添加和删除图片
今天和大家分享图片列表添加和删除图片的原型模板,效果包括: 点击图片列表的加号可以显示图片选择器,选择里面的图片; 选择图片后点击添加按钮,可以将该图片添加到图片列表; 鼠标移入图片列表的图片&…...

C++ 变量和基本类型
1、变量的声明和定义 1.1、变量声明规定了变量的类型和名字。定义初次之外,还申请存储空间,也可能会为变量赋一个初始值。 如果想声明一个变量而非定义它,就在变量名前添加关键字extern,而且不要显式地初始化变量: e…...
